Author: Denis Avetisyan
New statistical methods promise to sharpen the search for dark matter by optimizing detector alignment and analysis of subtle time-dependent signals.
This review details a statistical framework for maximizing sensitivity to daily and annual modulation in direct detection experiments using Fisher information and likelihood analysis.
Despite decades of searching, conclusive evidence for dark matter remains elusive, necessitating novel approaches to direct detection experiments. This work, ‘Statistics of Daily Modulation in Dark Matter Direct Detection Experiments’, presents a statistical framework for maximizing the sensitivity of these experiments by optimizing detector orientations and analysis techniques to enhance the detection of both annual and, crucially, daily modulation signals. We demonstrate that careful consideration of detector anisotropy and background estimation can significantly improve discovery potential, scaling with exposure time without saturation due to systematic uncertainties. Could this refined approach unlock the subtle signatures of dark matter interactions currently hidden within experimental data, and what further optimizations await exploration?
The Elusive Signal: Confronting Background Noise in Dark Matter Detection
The search for dark matter hinges on detecting the incredibly faint signals produced when weakly interacting massive particles (WIMPs) – hypothetical constituents of dark matter – occasionally collide with ordinary matter. However, these interactions are predicted to be exceptionally rare, occurring perhaps only a few times in years for even the largest detectors. This makes the task akin to finding a single firefly in a stadium filled with bright lights, as detectors are constantly bombarded by background events – interactions from cosmic rays, radioactive decay within detector materials, and other sources. These background signals can easily overwhelm any potential dark matter signal, necessitating sophisticated shielding, event selection techniques, and meticulous analysis to distinguish between genuine interactions and the constant “noise” of the universe. Consequently, the sensitivity of direct detection experiments is fundamentally limited by the ability to accurately characterize and subtract these overwhelming backgrounds.
The pursuit of dark matter through direct detection experiments demands exceptionally precise background modeling, as the signals sought are incredibly faint and easily mimicked by commonplace events. However, conventional approaches to this modeling often rely on simplifying assumptions – notably, the presumption of a stable, consistent background rate over extended periods. This simplification, while easing computational burdens, can introduce systematic uncertainties that ultimately obscure or falsely suggest dark matter interactions. Variations in detector materials, environmental factors, and even the accumulation of radioactive isotopes within the detector itself can cause background rates to fluctuate, invalidating the initial constant-rate assumption and requiring more sophisticated, dynamic models to accurately characterize the noise floor of these sensitive experiments. Consequently, a failure to address these complexities can lead to either missed detections or, more concerningly, false-positive signals attributed to dark matter when they are, in fact, merely misidentified background events.
Conventional analyses in direct dark matter detection often streamline calculations by presuming a consistent background event rate over time. However, real-world detectors are subject to a variety of fluctuating influences, including variations in detector materials, environmental radioactivity, and even the accumulation of cosmic ray-induced isotopes. This simplification can introduce systematic errors, as subtle temporal dependencies within the background spectrum may be misinterpreted as potential dark matter signals. Sophisticated modeling now incorporates time-varying background rates, accounting for these complexities through detailed simulations and the continuous monitoring of detector conditions to more accurately isolate the faint whispers of dark matter interactions.
The pursuit of dark matter through direct detection hinges on discerning incredibly faint signals from a pervasive background ‘noise’ – events that mimic dark matter interactions. Consequently, a thorough understanding and meticulous mitigation of these backgrounds are not merely helpful, but fundamentally essential for a conclusive search. Detectors are often situated deep underground to shield against cosmic rays, but residual radioactivity within detector materials and environmental sources continue to generate background events. Sophisticated modeling attempts to predict and subtract these contributions, however, inaccuracies in these models can easily masquerade as a dark matter signal, or obscure a genuine detection. Researchers are therefore continually refining background estimation techniques, employing advanced statistical methods and innovative detector designs to minimize uncertainties and enhance the sensitivity of dark matter experiments. Ultimately, the robustness of any dark matter claim relies heavily on the degree to which these background complexities have been accounted for and effectively controlled.
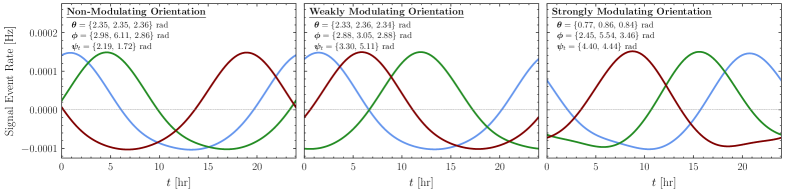
Unveiling Temporal Dependencies: Advanced Analysis Techniques
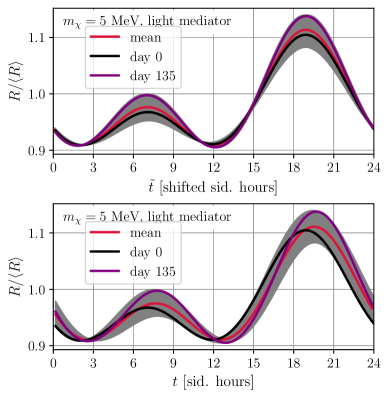
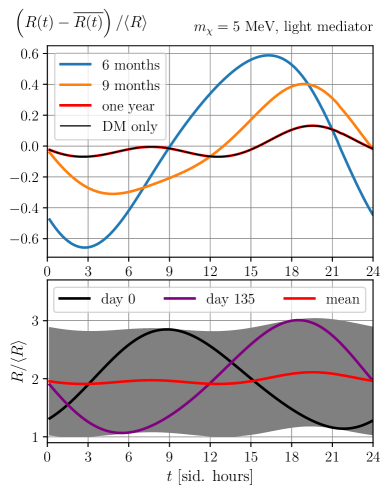
The theoretical interaction between dark matter particles and terrestrial detectors results in a predicted annual modulation of the event rate due to the Earth’s orbital motion through the galactic dark matter halo. Specifically, as the Earth moves through the halo, the relative velocity between the Earth and the dark matter wind varies, peaking around June 2nd and reaching a minimum around December 21st. This velocity variation directly impacts the expected interaction rate, leading to a corresponding modulation in the observed signal. Consequently, data analysis must account for this time-dependent effect; static analysis techniques will underestimate the potential signal and introduce systematic errors. The modulation is typically modeled as a cosine function with a period of one year and a phase determined by the Earth’s orbital parameters.
Sidereal stacking is a data analysis technique used in direct dark matter detection experiments to enhance the visibility of the expected daily modulation signal. This modulation arises from the Earth’s annual motion through the galactic dark matter halo, creating a ‘wind’ of dark matter particles. Sidereal stacking coherently adds data points based on the sidereal time – the time relative to distant stars – effectively aligning events expected from the dark matter wind. By summing data aligned to the Earth’s velocity relative to the dark matter halo, the signal is amplified while random background events are suppressed, increasing the signal-to-noise ratio and improving sensitivity to the weakly interacting dark matter particles. The process assumes a consistent dark matter wind direction relative to the detector over the stacking period.
Accurate background modeling is essential in direct dark matter detection experiments due to the presence of time-varying contributions that can mimic a signal. These backgrounds, often originating from detector materials and environmental factors, are not static and can exhibit daily or seasonal modulations. Failing to precisely characterize these modulated backgrounds introduces systematic errors in signal extraction, potentially leading to false positives or obscuring a genuine dark matter interaction. Sophisticated techniques are therefore employed to model these time-dependent backgrounds, often utilizing parameterized functions fitted to calibration data or utilizing complex simulations. The precision of this modeling directly impacts the experiment’s sensitivity and ability to confidently identify a dark matter signal.
A Poisson Likelihood framework is employed to quantify the probability of observing a given dataset, considering both background and potential signal contributions. This method is particularly suitable due to the discrete and count-based nature of the expected signal and background events. The likelihood function, based on the Poisson distribution, assesses how well the modeled event rate-summing contributions from both background and signal-predicts the observed number of events in each time bin or energy interval. Maximizing this likelihood, or equivalently minimizing the negative log-likelihood, provides estimates for the signal parameters and their uncertainties, while accounting for statistical fluctuations inherent in the detection process. The framework allows for a rigorous statistical evaluation of the evidence for a signal, incorporating systematic uncertainties through profiling or marginalization of nuisance parameters.
Establishing Statistical Rigor: Quantifying Sensitivity
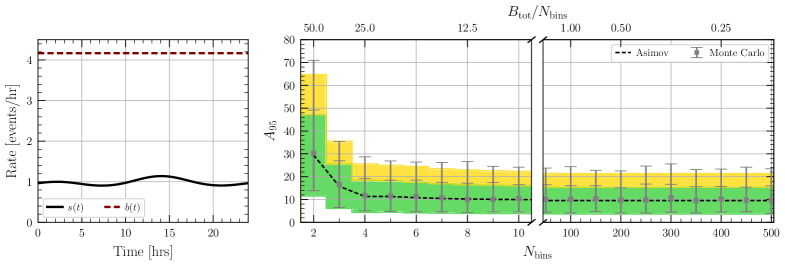
Fisher Information, denoted as F, quantifies the amount of information that observable data carries about an unknown parameter – in this context, typically the signal strength or interaction cross-section. Mathematically, it is defined as the expected value of the squared second derivative of the log-likelihood function with respect to the parameter of interest. A higher F value indicates greater sensitivity, meaning the data provides stronger constraints on the parameter. Specifically, the Cramer-Rao lower bound states that the variance of any unbiased estimator of the parameter is bounded from below by 1/F; therefore, a larger Fisher Information directly corresponds to a smaller achievable uncertainty in parameter estimation. Projections of experiment sensitivity are thus directly informed by calculations of Fisher Information, allowing researchers to predict the minimum detectable signal before experimental data is acquired.
Asymptotic projections, calculated from the Fisher Information matrix, provide a statistically sound method for estimating the minimum detectable signal strength in an experiment. This approach leverages the curvature of the likelihood function around its maximum to approximate the uncertainty in parameter estimation; a larger Fisher Information value indicates a more sharply peaked likelihood and therefore a smaller expected uncertainty. Specifically, the minimum detectable signal strength is often defined as the signal level corresponding to a one-sigma fluctuation of the estimated signal, determined by taking the square root of the inverse of the Fisher Information related to the signal parameter. This method assumes that the likelihood function is approximately Gaussian in the vicinity of the maximum likelihood estimate, which is valid for sufficiently large datasets and well-behaved models; it provides a rapid, albeit approximate, assessment of experimental sensitivity prior to full statistical analysis.
The Neyman Construction procedure establishes a statistically rigorous method for quantifying uncertainty in dark matter interaction rates. This approach defines a confidence interval – a range of plausible values for the interaction rate – by identifying the set of values for which the likelihood function is greater than or equal to a specified threshold, typically determined by the desired confidence level (e.g., 90% or 95%). When no signal is observed, the Neyman Construction yields an upper limit on the interaction rate, representing the value above which the hypothesis of no signal would be rejected at the chosen confidence level. This method avoids assumptions about the underlying probability distribution of the signal and provides a frequentist approach to statistical inference, ensuring the long-run validity of the reported confidence intervals and limits. The procedure relies on the ordering of p-values to define the acceptance region for the parameter of interest, thus providing a statistically sound framework for interpreting null results in dark matter searches.
Maximum Likelihood Estimation (MLE) is a fundamental statistical method used to determine the values of parameters within a defined model that best explain a set of observed data. In the context of dark matter detection, MLE is applied to both the signal – representing potential interactions – and background – encompassing all other contributing events. The process involves constructing a likelihood function, which quantifies the probability of observing the data given specific parameter values. The parameter set that maximizes this likelihood function is considered the best-fit, providing estimates for quantities such as the dark matter interaction cross-section and the background event rate. \mathcal{L}( \theta | x ) = \prod_{i=1}^{n} f(x_i ; \theta) , where θ represents the parameters being estimated and f(x_i ; \theta) is the probability density function for each data point x_i . MLE provides not only point estimates but also forms the basis for calculating uncertainties and confidence intervals associated with the fitted parameters.
Optimizing Background Models for Enhanced Sensitivity
Conventional dark matter searches often streamline data analysis by treating background events as statistically independent, a simplification that eases computational burdens. However, this approach introduces a critical vulnerability: correlations between background sources – arising from shared detector components, environmental factors, or even the decay chains of specific isotopes – are routinely ignored. Consequently, the true uncertainty in background estimation is underestimated, leading to a potentially inflated signal significance for any observed dark matter interaction. This underestimation can mimic a dark matter signal, creating false positives and hindering the accurate identification of genuine interactions. Rigorous analysis must therefore move beyond the assumption of independence, employing techniques that accurately capture and account for these correlations to ensure the reliability of dark matter searches.
The principle of combining individual detector sensitivities through simple harmonic addition – a common practice in dark matter searches – rests on the fundamental assumption that background events in each detector are statistically independent. However, this approach yields inaccurate results if correlations exist between these backgrounds; for example, a common environmental noise source impacting multiple detectors simultaneously. When backgrounds are not independent, the combined sensitivity is overestimated, potentially masking a genuine dark matter signal or leading to spurious detections. Therefore, a thorough understanding and careful modeling of background correlations are essential for correctly interpreting experimental data and achieving the highest possible sensitivity in direct dark matter searches. Failing to account for these dependencies introduces systematic uncertainties that can significantly degrade the experiment’s ability to probe the parameter space for weakly interacting massive particles.
The pursuit of elusive dark matter relies heavily on distinguishing faint interaction signals from the constant ‘noise’ of background events; therefore, precisely characterizing these backgrounds is paramount. Backgrounds aren’t static, however, often exhibiting subtle, time-dependent modulations due to factors like seasonal variations in cosmic ray flux or detector-specific effects. Failing to accurately model these modulations introduces systematic errors that can mimic or obscure genuine dark matter signals, leading to false positives or missed detections. Sophisticated analysis techniques are thus employed to track these changes, often utilizing advanced statistical methods and requiring extensive calibration data. A robust understanding of these modulated backgrounds isn’t merely a matter of reducing noise; it directly translates into an increased ability to probe weaker interaction strengths and expand the search space for dark matter particles, ultimately maximizing the potential for discovery.
A novel framework for dark matter detection has yielded a substantial increase in sensitivity, achieving up to a sixfold improvement over existing methods. This advancement stems from a meticulous optimization of detector orientations, strategically aligning them to maximize signal capture while minimizing noise. Crucially, the framework incorporates a detailed accounting of time-varying backgrounds – fluctuations in environmental radiation and other interfering signals – that previously obscured faint interactions. By accurately modeling these temporal changes and correlating them with detector responses, the system effectively filters out false positives and enhances the ability to identify the elusive signatures of dark matter particles. This refined approach not only boosts the likelihood of detection but also reduces the uncertainties associated with data analysis, paving the way for more precise and reliable measurements in the ongoing search for this fundamental component of the universe.
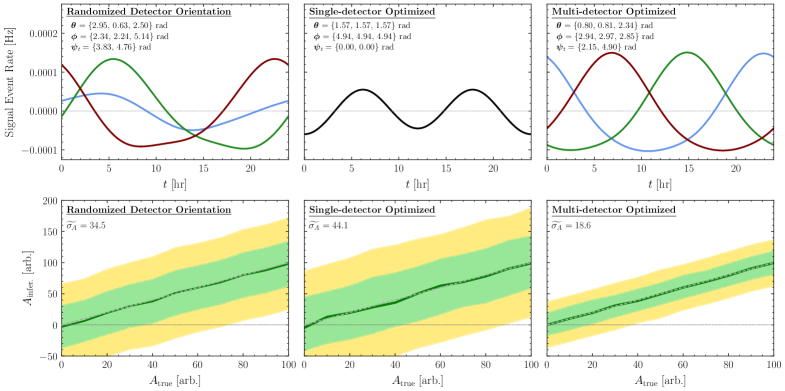
The pursuit of dark matter detection, as detailed in the study, demands a rigorous adherence to statistical principles. It’s not merely about registering a signal, but about establishing the certainty of its origin and magnitude. This aligns with Michel Foucault’s observation: “Truth is not something given to us; it is something we produce.” The paper’s development of a statistical framework-specifically, maximizing the modulation amplitude through optimized detector orientations and likelihood analysis-is a deliberate production of verifiable evidence. The methodical approach to signal extraction, focusing on the consistency of boundaries and predictability of the data, underscores the importance of a provable solution, mirroring the elegance found in a mathematically pure algorithm. The Fisher Information analysis, in particular, provides a quantifiable measure of this certainty, a cornerstone of the study’s contribution.
The Path Forward
The presented formalism, while rigorous in its treatment of directional dark matter signal extraction, ultimately highlights the persistent tension between statistical ambition and experimental reality. The pursuit of increasingly precise modulation amplitude estimates, predicated on ideal detector response and negligible systematic errors, risks becoming a purely theoretical exercise. A detector’s capacity to truly resolve the subtle daily modulation-a consequence of Earth’s motion, not some inherent particle property-remains the critical, and often unaddressed, bottleneck.
Future work should not solely concentrate on refining the Fisher information analysis or exploring exotic modulation signatures. Instead, emphasis must be placed on quantifying, and ultimately minimizing, the sources of noise that obscure the signal. The current framework assumes a perfectly known detector response; a demonstrably false premise. A deeper investigation into methods for self-calibration, and the development of noise models that accurately reflect the limitations of existing technologies, represent a more fruitful avenue for progress.
The elegance of a mathematically sound solution should not eclipse the pragmatic demands of experimentation. It is, after all, a signal detected, not merely predicted, that will confirm the existence of dark matter. The pursuit of mathematical purity, while admirable, must remain tethered to the messy, imperfect world of physical measurement.
Original article: https://arxiv.org/pdf/2602.15947.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Netflix’s Stranger Things Replacement Reveals First Trailer (It’s Scarier Than Anything in the Upside Down)
- The Best Members of the Flash Family
- ‘Crime 101’ Ending, Explained
- 7 Best Animated Horror TV Shows
- Arknights: Endfield launches January 22, 2026
- How to Froggy Grind in Tony Hawk Pro Skater 3+4 | Foundry Pro Goals Guide
- 32 Kids Movies From The ’90s I Still Like Despite Being Kind Of Terrible
- Wife Swap: The Real Housewives Edition Trailer Is Pure Chaos
- 10 Best Anime to Watch if You Miss Dragon Ball Super
2026-02-19 22:08