![The study posits an exotic interaction between electrons in both [latex] ^4He [/latex] and [latex] ^3He [/latex], mediated by a novel boson, and crucially demonstrates that this electron-electron interaction-despite differing nuclear structures-produces identical leading-order energy shifts in both isotopes, suggesting a fundamental, isotope-independent quantum effect.](https://arxiv.org/html/2602.09743v1/x1.png)
A decades-old puzzle involving helium’s ionization energy continues to challenge our understanding of fundamental physics and is narrowing the possibilities for exotic interactions beyond the Standard Model.
Researchers have directly observed the three-dimensional Anderson transition in ultracold atoms, providing crucial experimental validation of decades-old theoretical predictions about how disorder affects material properties.
A new study reveals how the quantum behavior of protons in hydrogen-bonded materials subtly alters the way they absorb and emit light.
New research demonstrates that tracking how structures form in the universe is crucial to understanding the evolving nature of dark energy, going beyond simple measurements of cosmic expansion.
(M+1)[/latex] or [latex](M-1)(M-1)[/latex] block, a dynamic echoing the fundamental instability inherent in any theoretical construct-a principle first outlined by Penrose in 1971.](https://arxiv.org/html/2602.08341v1/x1.png)
A new approach to loop quantum gravity proposes that spacetime itself emerges directly from the interactions of matter fields.
New research explores whether the decay of positronium, when analyzed through Compton scattering and mirror symmetry, reveals fundamental limitations to our understanding of locality and realism.
![Hankel functions, parameterized by the ratio [latex]\omega/\alpha[/latex], define the spectral response of a polarizer, with the magnitude squared of the first-order Hankel transform [latex]|H^{(1)}_{iy}(ix)|^{2}[/latex] serving as a quantifiable metric for frequency quantization at the boundary condition.](https://arxiv.org/html/2602.07323v1/fig4.png)
New research demonstrates how boundary conditions shape the energy spectrum of quantum fields in accelerated frames, offering insights into particle creation.
Recent advancements leverage the unique properties of Rydberg atoms to explore the fascinating realm of non-Hermitian physics and its implications for quantum technologies.
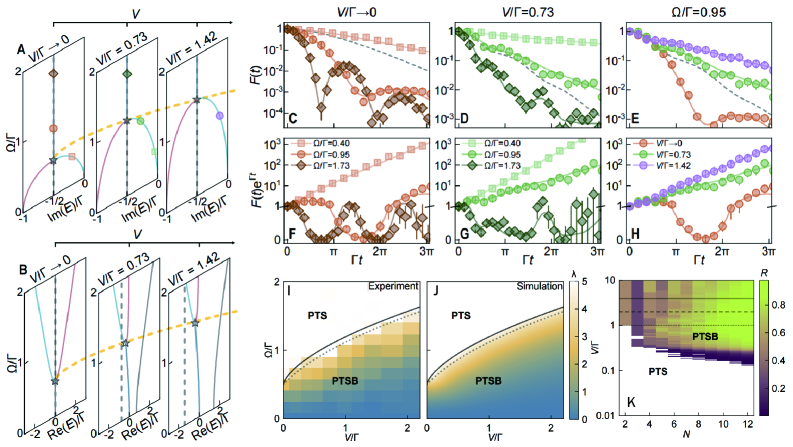
![A one-dimensional model of black hole evaporation, realized through an engineered spin chain with site-dependent couplings, demonstrates a transition from the predicted linear growth of Hawking radiation-characteristic of semiclassical behavior-to a downturn and eventual decay to zero as the black hole completes evaporation, mirroring the Page curve and indicating a potential resolution to the information paradox when approximately half of the particles have radiated away [latex] t_{P} [/latex].](https://arxiv.org/html/2602.07043v1/x1.png)
New research demonstrates the transfer of quantum information across an event horizon-like boundary in a tabletop experiment, shedding light on the long-standing black hole information paradox.
![The study investigates the relationship between a ManaMM detector’s energy gap and the holographic quantization of a dual scalar sector within a three-dimensional conformal field theory, demonstrating that a local bulk detector approaching the boundary does not generally replicate the results of a local boundary-detector protocol-a finding illustrated by comparing admissible holographic quantizations [latex]\Delta = \Delta_{\pm}[/latex] with bulk AdS curves.](https://arxiv.org/html/2602.07895v1/x1.png)
A new framework utilizes localized quantum detectors to investigate the subtle differences between holographic quantum gravity models.