Dark Matter’s Grip on Black Holes: A New Look at Particle Behavior

Author: Denis Avetisyan

A new study explores how the presence of a Hernquist dark matter halo alters the spacetime around black holes, influencing the fate of particles in their vicinity.

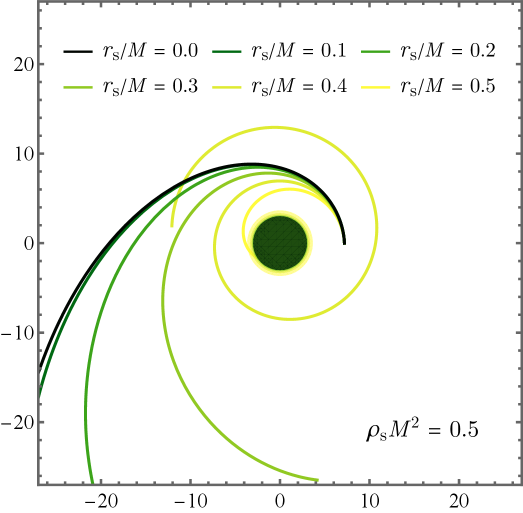
The simulation tracks particle movement within the distorted spacetime around a black hole situated in a Hernquist dark matter halo, demonstrating how variations in scale radius-at a density of 0.5-influence trajectory patterns.

This review examines particle production, absorption, scattering, and geodesic motion within the gravitational field of a Schwarzschild-Hernquist black hole.

The standard Schwarzschild metric, while foundational, fails to capture the influence of surrounding dark matter distributions on black hole spacetime. This is addressed in ‘Particle production, absorption, scattering, and geodesics in a Schwarzschild–Hernquist black hole’, which investigates the quantum and classical effects arising from embedding a Schwarzschild black hole within a Hernquist dark matter halo. Our analysis reveals that the presence of dark matter significantly modifies particle creation rates, alters scattering cross-sections, and impacts the trajectories of both massless and massive particles. How do these modifications affect our understanding of black hole evaporation and the ultimate fate of information in astrophysical settings?

The Illusion of Empty Space: Framing the Black Hole Problem

Accurately modeling the dynamic interplay of black holes hinges on a complete and precise description of the spacetime surrounding them. This isn’t simply a matter of locating objects in space, but understanding how mass and energy warp the very fabric of spacetime, dictating the paths of light and matter. Spacetime geometry, mathematically defined by the metric tensor, determines gravitational forces and, consequently, the orbital paths and potential collisions of black holes. Deviations from a perfectly flat spacetime, as described by $g_{\mu\nu}$ , arise from the presence of mass-energy, and become particularly significant near black holes where gravitational effects are extreme. Therefore, a thorough understanding of this geometry – encompassing not only the black hole itself but also any surrounding matter distribution – is paramount for predicting their behavior and interpreting observational data from gravitational wave detectors and electromagnetic telescopes.

The Schwarzschild solution, a cornerstone of general relativity, initially depicts spacetime around a non-rotating, uncharged black hole as solely dictated by its mass. However, this simplification diverges from cosmological reality, as black holes invariably reside within galaxies embedded in substantial dark matter halos. Accurately modeling black hole interactions, therefore, demands accounting for the gravitational influence of this surrounding dark matter. The presence of dark matter alters the spacetime geometry, impacting not only the orbits of objects near the black hole but also the black hole’s own motion and potential for collisions. Consequently, researchers move beyond the isolated Schwarzschild metric to incorporate realistic dark matter distributions, creating a more comprehensive and physically relevant framework for understanding black hole dynamics in the universe.

The distribution of dark matter significantly alters the spacetime around black holes, necessitating models beyond the simplified Schwarzschild metric. The Hernquist profile provides a physically plausible representation of this influence, describing a dark matter halo with a density that decreases as the inverse square of the radius $\rho(r) \propto r^{-1}$ . This profile is motivated by N-body simulations of galaxy formation, suggesting a natural outcome of hierarchical structure formation where smaller dark matter halos merge to form larger ones. Unlike isothermal or uniform distributions, the Hernquist halo’s decreasing density avoids the core singularities often found in other models, resulting in a more realistic and mathematically tractable spacetime metric for studying black hole interactions within a galactic environment. Consequently, incorporating the Hernquist profile allows for more accurate predictions of phenomena like gravitational lensing, orbital precession, and the dynamics of stars near supermassive black holes.

Accurately forecasting the dynamics of black holes demands a comprehensive description of the spacetime around them, and this necessitates defining a composite metric that accounts for all contributing mass distributions. While the Schwarzschild metric elegantly describes spacetime around an isolated black hole, the universe is rarely so simple. The presence of dark matter, a non-luminous substance comprising a significant portion of the universe’s mass, profoundly alters this geometry. Constructing a metric that integrates the gravitational influence of both the black hole and surrounding dark matter – often modeled using physically realistic profiles like the Hernquist halo – is therefore paramount. This composite metric isn’t merely a mathematical exercise; it directly dictates how light and matter move in the vicinity of the black hole, influencing observable phenomena such as gravitational lensing, orbital precession, and the emission of gravitational waves. Without this precise geometrical framework, predictions regarding black hole behavior remain fundamentally incomplete and potentially inaccurate, hindering efforts to test general relativity and understand the cosmos.

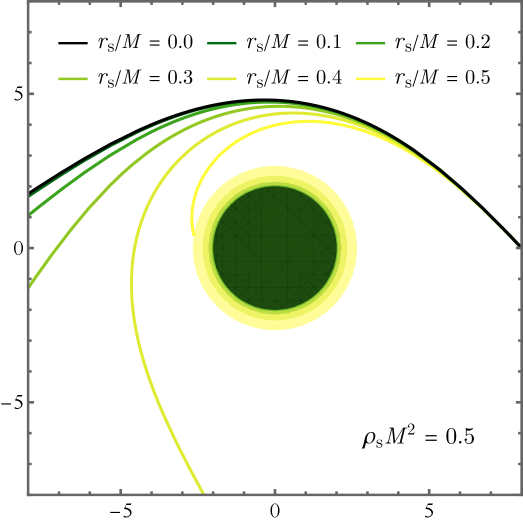
Photon trajectories around a black hole embedded in a Hernquist dark matter halo are significantly affected by variations in the density parameter, even while maintaining a fixed scale radius of 0.5.

Mapping the Field: A Mathematical Framework

The theoretical framework for analyzing interactions utilizes a Massless Scalar Field, described by a wave equation within the specified spacetime geometry. This field, denoted by φ, satisfies the Klein-Gordon equation in curved spacetime: $\nabla^2 \phi - \frac{1}{\sqrt{-g}} \partial_\mu (\sqrt{-g} \partial^\mu \phi) = 0$ , where $g$ is the determinant of the metric tensor. The massless nature simplifies analysis while still allowing for the investigation of field propagation and response to gravitational and other potential influences within the defined spacetime. This approach allows us to model interactions as disturbances in the scalar field, enabling a mathematical description of their behavior.

The Separable Ansatz is a mathematical technique used to simplify the wave equation for the Massless Scalar Field by assuming the field can be expressed as a product of functions, each dependent on a single coordinate. Specifically, the field $\Phi(t, r, \theta, \phi)$ is decomposed into $\Phi(t, r, \theta, \phi) = R(r)Y(\theta, \phi)$ , where $R(r)$ represents the radial dependence and $Y(\theta, \phi)$ describes the angular dependence. This separation allows for the transformation of the original partial differential equation into a set of simpler ordinary differential equations, one governing the radial component and another (typically the spherical harmonics equation) governing the angular component. By focusing solely on the radial equation, the problem is significantly reduced in complexity, enabling analysis of how the field behaves as a function of distance from the origin.

The Radial Equation is a second-order ordinary differential equation derived from the separation of variables applied to the wave equation for a massless scalar field in a spherically symmetric spacetime. Specifically, it describes the behavior of the field variable, typically denoted as $R(r)$ , as a function of the radial coordinate $r$ . The equation takes the form $\frac{d^2R}{dr^2} + \left(\frac{2}{r}\right)\frac{dR}{dr} + \left[k^2 - V_{eff}(r)\right]R = 0$ , where $k$ is the comoving momentum and $V_{eff}(r)$ represents the effective potential. Solutions to this equation determine the allowed modes of the field and their spatial distribution, effectively modeling how the field propagates outwards from a source as a function of distance from the center of the spacetime.

The Effective Potential, denoted as $V_{eff}(r)$ , appearing within the Radial Equation, is a crucial component in determining the field’s behavior. It is constructed by summing the contribution from the spacetime curvature, represented by terms derived from the metric, and the gravitational potential of the dark matter halo, typically modeled as a function of radial distance $V_{DM}(r)$ . Specifically, $V_{eff}(r) = V_{curvature}(r) + V_{DM}(r)$ . This potential dictates the allowed energy levels and influences the scattering and binding properties of the massless scalar field within the combined gravitational environment of both spacetime and the dark matter distribution.

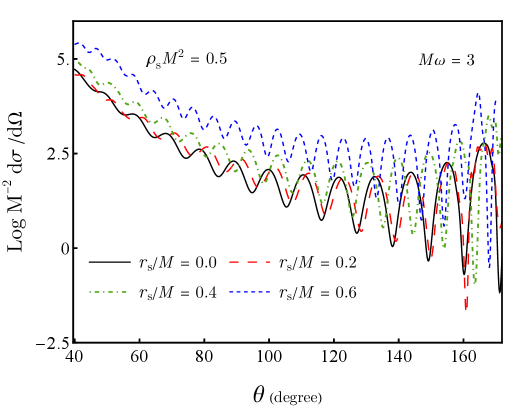
The total scattering cross section, displayed on a logarithmic scale for a Hernquist black hole at a fixed frequency, varies predictably with both the density parameter <span class="katex-eq" data-katex-display="false">{\rho_s}M^2</span> and the scaled radius <span class="katex-eq" data-katex-display="false">{r_s}/M</span>. — The total scattering cross section, displayed on a logarithmic scale for a Hernquist black hole at a fixed frequency, varies predictably with both the density parameter ${\rho_s}M^{2}$ and the scaled radius ${r_s}/M$ .

Tracing the Signal: Scattering Analysis and Boundary Conditions

The solutions to the Radial Equation, describing field behavior near a black hole, are constrained by specific boundary conditions to ensure physical relevance. At the event horizon $r_H$ , only purely ingoing waves are permitted, preventing unphysical divergences and reflecting the one-way nature of the horizon. Conversely, at spatial infinity $r \rightarrow \in fty$ , the solutions must represent a superposition of an incident wave and a reflected wave. This reflects the expectation that a wave impinging on the black hole will be partially scattered back and partially absorbed. The amplitudes of these incident and reflected waves are determined by the specific form of the solution and dictate the overall scattering behavior of the black hole.

The Reflection Coefficient ( $R(\omega, l)$ ) and Transmission Coefficient ( $T(\omega, l)$ ) are directly determined by the imposed boundary conditions on the radial equation solution. These coefficients quantify the amplitude of the scattered and transmitted waves, respectively, as a function of the wave frequency ω and angular momentum quantum number $l$ . Specifically, $R(\omega, l)$ represents the proportion of the incident wave that is reflected back from the black hole, while $T(\omega, l)$ indicates the proportion that is transmitted through the event horizon or scattered to infinity. The functional form of these coefficients is crucial for characterizing the scattering process and ultimately determining the black hole’s response to external perturbations.

The phase shift, denoted as $\delta(k)$ , quantifies the change in the asymptotic phase of the scattered wave function due to the interaction with the black hole potential. It is a function of the wave number $k$ and directly relates to the scattering amplitude $f(k)$ via the equation $f(k) = \frac{1}{k}e^{2i\delta(k)}$ . A non-zero phase shift indicates that the scattered wave is not simply a delayed version of the incident wave, but has undergone a fundamental alteration in its phase due to the gravitational interaction. Analyzing the energy dependence of $\delta(k)$ provides insights into the strength and nature of the scattering process, and is crucial for calculating observable quantities like the scattering cross-section.

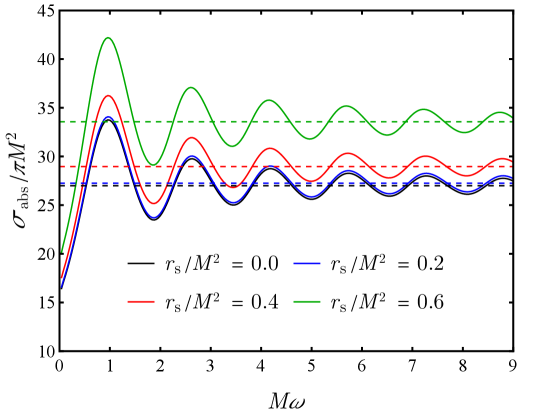
The Partial Wave Expansion provides a method for calculating the Scattering Cross Section and Absorption Cross Section, which directly quantify the probabilities of scattering and absorption events. Analysis reveals that the scale radius, $r_s/M$ , exerts a more significant influence on these cross sections than the density parameter, $\rho_s M^2$ . This indicates that the overall size of the scattering center, as defined by the Schwarzschild radius relative to the mass, is a primary determinant of scattering and absorption, exceeding the impact of variations in density when characterizing the interaction.

$Partial absorption cross sections, plotted as a function of M\omega for \ell = 0, 1, and 2, reveal that varying the Hernquist parameters \frac{r_s}{M} and \frac{\rho_s M^2}{M} modulates the absorption profile.$

Partial absorption cross sections, plotted as a function of

M\omega

for

\ell

= 0, 1, and 2, reveal that varying the Hernquist parameters

\frac{r_s}{M}

and

\frac{\rho_s M^2}{M}

modulates the absorption profile.

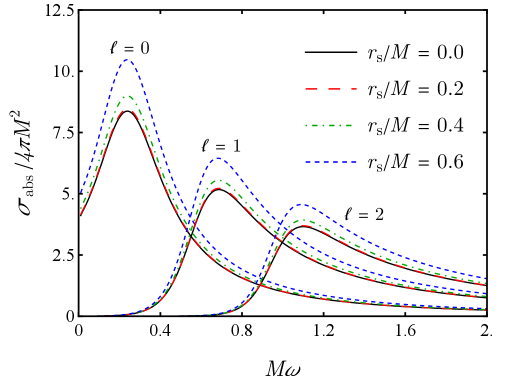
The Devil in the Details: Geodesics and Hawking Radiation

The behavior of anything – from photons to planets – in the vicinity of a black hole is dictated by geodesic motion, essentially the paths of least resistance through curved spacetime. Unlike straight lines in flat space, geodesics around black holes are bent and twisted by the intense gravity, describing how objects fall towards – or orbit – these cosmic singularities. Calculating these paths involves solving the geodesic equation, a complex mathematical relationship that accounts for the warping of spacetime caused by the black hole’s mass. This isn’t merely an academic exercise; understanding geodesic motion is fundamental to predicting how light bends around black holes – a phenomenon known as gravitational lensing – and how matter accretes onto them, forming swirling disks and powerful jets. Furthermore, analyzing different types of geodesics – those for massless particles like photons, and those for objects with mass – provides a complete picture of the diverse orbital possibilities and the ultimate fate of anything that ventures too close.

The behavior of objects – from photons to planets – in the vicinity of a black hole isn’t dictated by traditional Newtonian gravity, but by following paths of shortest distance within curved spacetime. These paths are mathematically described by the geodesic equation, a cornerstone of general relativity. Crucially, this equation isn’t simply about moving in a straight line; it incorporates the warping of spacetime itself through terms called Christoffel Symbols. These symbols aren’t constants, but rather functions that quantify the curvature at each point in spacetime, effectively telling an object how to deviate from a straight line due to the gravitational influence of massive bodies. The geodesic equation, therefore, provides a precise framework for understanding how gravity bends light, alters planetary orbits, and governs the motion of everything caught in the gravitational well of a black hole, accounting for the complex geometry of the universe.

A comprehensive understanding of orbital dynamics near black holes necessitates the investigation of both massless and massive particle trajectories. Null geodesics, which describe the paths of photons and other particles traveling at the speed of light, reveal how light bends and orbits within the intense gravitational field, influencing observable phenomena like gravitational lensing and the accretion disk structure. Simultaneously, timelike geodesics chart the courses of massive particles – from stars and planets to spacecraft – demonstrating how their orbits deviate from Newtonian predictions due to spacetime curvature. By analyzing both types of geodesics, scientists can reconstruct a complete picture of orbital behavior, predicting not only the stability of orbits but also the frequencies of emitted gravitational waves and the eventual fate of matter falling into the black hole. This dual approach is crucial for accurately modeling astrophysical processes and testing the predictions of general relativity in extreme gravitational environments.

Theoretical calculations indicate that black holes are not entirely black, but rather emit Hawking radiation – a process fundamentally linked to quantum effects near the event horizon and described effectively using coordinates such as Painlevé-Gullstrand. This emission results in a gradual decrease of the black hole’s mass, prompting investigation into the ultimate fate and potential existence of a stable remnant. Calculations reveal the Hawking Temperature to be $1/(8πM) + (-Mr³s - r⁴s)ρsM/(2M + rs)²$ , a value deviating from the strictly thermal profile predicted by the simpler Schwarzschild geometry. To ensure physical viability, parameter space is constrained to guarantee a positive remnant mass, calculated as $πρsrs³ + πρsrs² - rs$ , suggesting that even as black holes evaporate through Hawking radiation, a minimal, stable mass might remain.

Total absorption cross sections vary with frequency <span class="katex-eq" data-katex-display="false">M\omega</span>, exhibiting a dependence on either a fixed normalized scale radius <span class="katex-eq" data-katex-display="false">r_{\text{s}}/M = 0.1</span> (left) or a fixed density parameter <span class="katex-eq" data-katex-display="false">\rho_{\text{s}}M^{2} = 0.1</span> (right), as compared to the geometric absorption cross sections (dashed lines). — Total absorption cross sections vary with frequency $M\omega$ , exhibiting a dependence on either a fixed normalized scale radius $r_{\text{s}}/M = 0.1$ (left) or a fixed density parameter $\rho_{\text{s}}M^{2} = 0.1$ (right), as compared to the geometric absorption cross sections (dashed lines).

The study of particle behavior around black holes, particularly when factoring in the complexities of dark matter halos, reveals a humbling truth. It’s not about pristine theoretical models; it’s about what survives contact with reality. The researchers meticulously calculate absorption and scattering cross sections, chasing ever-refined predictions, yet the underlying spacetime itself is a compromise-a Schwarzschild metric bent and shaped by the messy influence of a Hernquist halo. As Confucius observed, “The superior man is modest in his speech, but exceeds in his actions.” These calculations aren’t about boasting elegant equations; they’re about the painstaking work of describing what actually happens when a particle dares to approach an event horizon, and acknowledging the inevitable deviation between theory and observation. Everything optimized will one day be optimized back, and this research is a testament to that cycle.

Sooner or Later, It All Leaks

The predictable dance of particles around a modified Schwarzschild geometry, even one adorned with a Hernquist halo, offers little genuine surprise. The calculations will become more elaborate, the partial wave analyses more granular, but the fundamental challenge remains: any model is a simplification, and production systems will invariably find the cracks. The pursuit of ever-more-accurate absorption and scattering cross sections is, fundamentally, an exercise in delaying the inevitable. If a bug is reproducible, it implies a stable system – a system ripe for exploitation when the inevitable unexpected input arrives.

The real question isn’t whether these calculations match observation – because matching observation is merely a temporary reprieve – but whether they illuminate the limits of the current framework. Black hole thermodynamics, as currently understood, feels less like a complete theory and more like a particularly elegant set of accounting tricks. Each refinement of the halo parameters simply pushes the point of failure further down the road.

Future work will undoubtedly focus on incorporating more ‘realistic’ dark matter distributions, perhaps even attempting to model non-spherically symmetric halos. This is, predictably, an invitation to add layers of complexity without addressing the underlying issue: documentation is collective self-delusion. Anything self-healing just hasn’t broken yet. The true test will not be in calculating geodesics, but in confronting the inevitable inconsistencies when this model meets a universe that refuses to be neatly categorized.

Original article: https://arxiv.org/pdf/2602.15420.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

The Illusion of Empty Space: Framing the Black Hole Problem

Mapping the Field: A Mathematical Framework

Tracing the Signal: Scattering Analysis and Boundary Conditions

The Devil in the Details: Geodesics and Hawking Radiation

Sooner or Later, It All Leaks

See also: