Author: Denis Avetisyan
New research explores how surrounding dark matter halos warp the spacetime around slowly rotating black holes, altering orbital dynamics and influencing gravitational wave signatures.
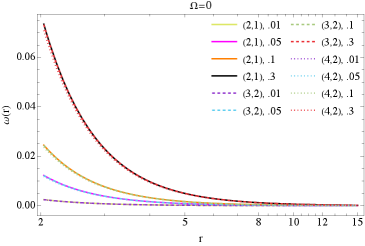
This study investigates the geometric effects of matter environments on the spacetime of slowly rotating black holes, focusing on epicyclic frequencies and potential implications for extreme mass-ratio inspirals.
Astrophysical black holes are rarely isolated, yet most strong-field tests of gravity assume vacuum spacetimes. This work, ‘Geometric properties of slowly rotating black holes embedded in matter environments’, constructs a self-consistent spacetime describing a slowly rotating black hole within a surrounding dark matter halo, modeled as an anisotropic fluid, revealing how environmental effects modify key orbital characteristics. We demonstrate that the presence and rotation of the halo induce measurable deviations in frame dragging, light ring locations, and epicyclic frequencies, potentially leaving observable imprints on gravitational wave signals. Could these subtle effects be disentangled by future space-based detectors, offering a novel probe of both gravity and the distribution of dark matter?
The Fabric of Spacetime: A Baseline for Delusion
A cornerstone of modern cosmology rests upon the ability to mathematically describe the very fabric of the universe – spacetime. Initial progress in understanding this geometry began with idealized solutions to Einstein’s field equations, most notably the Schwarzschild metric which describes spacetime around a non-rotating, spherically symmetric mass, and the Kerr metric which extends this to include rotation. These solutions, while representing simplified scenarios, provide fundamental building blocks for modeling more complex astrophysical objects like black holes. The Schwarzschild radius, R_s = \frac{2GM}{c^2}, defines the event horizon, a point of no return, while the Kerr metric introduces the concept of an ergosphere where spacetime itself is dragged along with the rotating black hole. These vacuum solutions aren’t merely theoretical constructs; they serve as essential starting points for investigating gravitational phenomena and understanding the universe’s large-scale structure, providing a baseline against which the effects of matter and energy can be rigorously assessed.
While foundational solutions to Einstein’s field equations, such as the Schwarzschild and Kerr metrics describing black holes, provide crucial insights into spacetime, their true manifestation in the universe is rarely isolated. These solutions invariably exist within complex gravitational environments, most notably embedded within expansive dark matter halos. These halos, comprising a significant portion of a galaxy’s mass, exert a substantial influence on the surrounding spacetime geometry, modifying the gravitational dynamics predicted by the vacuum solutions alone. The presence of dark matter alters the orbits of stars and gas, impacts the propagation of light, and even affects the event horizons of black holes. Consequently, accurately modeling astrophysical phenomena requires moving beyond idealized vacuum scenarios and incorporating the distribution and properties of these pervasive dark matter halos – a critical step towards a realistic understanding of the universe’s structure and evolution.
Accurate depictions of galactic environments demand a thorough understanding of dark matter distribution, as this unseen mass profoundly impacts gravitational interactions. While dark matter remains elusive, its effects are modeled using density profiles, with the Hernquist profile being a frequently employed example. This profile describes a density that increases towards the galactic center and then decreases with radius, offering a mathematically tractable way to represent the dark matter halo surrounding galaxies. By incorporating such profiles into spacetime models-like those derived from the Schwarzschild or Kerr metrics-researchers can move beyond idealized scenarios and investigate how dark matter influences phenomena such as gravitational lensing, orbital dynamics of stars, and the overall structure of galaxies. The Hernquist profile, with its adjustable parameters, allows for the exploration of diverse galactic configurations and provides a crucial link between theoretical models and observational data concerning the distribution of this mysterious substance.
Mapping the Dance: Geodesic Motion and Orbital Pathways
Geodesic motion, the calculation of test particle trajectories in a gravitational field, is fundamental to astrophysical modeling. This calculation determines the paths of objects influenced solely by gravity, neglecting non-gravitational forces. In the strong gravity regimes around black holes, geodesic motion predicts phenomena such as gravitational lensing, accretion disk dynamics, and the behavior of orbiting stars. Within galaxies, understanding geodesic motion is critical for modeling the orbits of stars and gas clouds in galactic potentials, including those modified by dark matter distributions. The equations governing geodesic motion are derived from the principles of general relativity, and their solutions provide insights into the spacetime geometry and the distribution of mass-energy. These calculations rely on solving the geodesic equation, a second-order differential equation described in curved spacetime, often expressed as \frac{d^2x^\mu}{d\tau^2} + \Gamma^\mu_{\alpha\beta}\frac{dx^\alpha}{d\tau}\frac{dx^\beta}{d\tau} = 0 , where x^\mu represents the spacetime coordinates, τ is the proper time, and \Gamma^\mu_{\alpha\beta} are the Christoffel symbols representing the gravitational effects of spacetime curvature.
The Hamilton-Jacobi formalism is a technique for solving equations of motion by transforming the problem into a scalar equation, the Hamilton-Jacobi equation. This approach utilizes a function, often denoted as S, representing the action, and expresses the system’s dynamics in terms of its gradients. Solving for S yields a complete solution describing the trajectory of a particle. The formalism is particularly advantageous for systems with conserved quantities, allowing for the reduction of the problem’s dimensionality and simplification of the calculations. In the context of geodesic motion, it enables precise prediction of orbital behavior around massive objects by effectively determining the particle’s path in spacetime, independent of coordinate choice. The method’s adaptability extends to complex scenarios, including those incorporating perturbations and relativistic effects, making it a cornerstone for analyzing orbital dynamics in astrophysics.
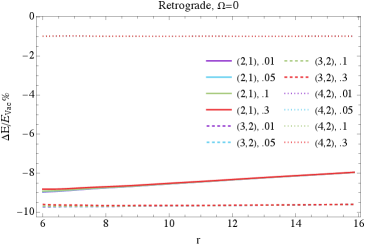
Calculations of geodesic motion allow for the precise determination of key orbital characteristics, notably the Innermost Stable Circular Orbit (ISCO) and the epicyclic frequency κ. The ISCO defines the closest stable orbit a test particle can maintain around a central mass; orbits within this radius are inherently unstable and lead to inspiral. The epicyclic frequency describes the rate of radial or vertical oscillations of a particle in a slightly perturbed circular orbit. Recent research utilizing these calculations quantifies the modifications to both the ISCO and κ caused by the gravitational potential of dark matter halos. Specifically, the presence of a dark matter halo generally decreases the ISCO radius and alters the epicyclic frequency, indicating a reduction in orbital stability compared to orbits around an isolated central mass. These changes are dependent on the halo’s density profile and mass distribution, providing a means to constrain dark matter models through orbital dynamics.
The slow rotation approximation is a technique used to simplify calculations in general relativity, particularly when modeling the effects of rotating massive objects on surrounding test particles. This approximation assumes that the angular velocity ω of the rotating body is much smaller than the speed of light c , allowing for terms proportional to \omega^2 and higher to be neglected. This significantly reduces the computational complexity when calculating metrics and geodesics, enabling the analysis of frame dragging – the effect where a rotating mass distorts spacetime, causing orbiting objects to precess. While introducing a degree of error, the slow rotation approximation provides reasonably accurate results for many astrophysical scenarios, such as the motion of stars around supermassive black holes, and serves as a crucial first step in more complex, high-order calculations.
Whispers from the Abyss: Extreme Mass Ratio Inspirals
Extreme Mass Ratio Inspirals (EMRIs) are gravitational wave events resulting from the inspiral of a compact object – typically a stellar-mass black hole, neutron star, or white dwarf – into a supermassive black hole (SMBH) with masses ranging from 105 to 1010 solar masses. The substantial mass ratio – often exceeding 104:1 – leads to a deep-strong-field regime where the smaller object completes thousands of orbits before plunging into the SMBH. This protracted inspiral generates gravitational waves with a characteristic frequency sweep, increasing in both amplitude and frequency as the smaller object spirals inward. The waveform’s frequency and amplitude are directly related to the masses and spins of the two black holes, and the emitted power is proportional to the eighth power of the mass ratio, making EMRIs particularly strong sources despite their relative rarity.
Gravitational waves emitted from Extreme Mass Ratio Inspirals (EMRIs) encode detailed information about the central supermassive black hole and its surrounding spacetime. The frequency and amplitude of the emitted waves are directly related to the black hole’s mass and spin. Furthermore, subtle variations in the waveform are sensitive to the geometry of spacetime, including the presence of any nearby objects or distortions. Analysis of these waveforms allows for precise measurements of the black hole’s parameters – mass, spin, and distance – and can also probe the nature of gravity in the strong-field regime, potentially revealing deviations from General Relativity. The waveform’s phase, in particular, is highly sensitive to these parameters, allowing for accurate parameter estimation with sufficient signal strength and detector sensitivity.
The detection and analysis of gravitational waves from Extreme Mass Ratio Inspirals (EMRIs) necessitate space-based gravitational wave observatories due to the low-frequency nature of the emitted signals. Ground-based detectors, such as LIGO and Virgo, are limited by seismic noise at the frequencies expected from EMRIs – typically in the millihertz range. The proposed Laser Interferometer Space Antenna (LISA) mission, consisting of three spacecraft forming an equilateral triangle with multi-kilometer arms, and the TianQin mission, utilizing three satellites in a highly elliptical orbit, are designed to overcome these limitations. These missions will employ laser interferometry to precisely measure the changes in distance between test masses, enabling the detection of the subtle spacetime ripples generated by EMRI events. The sensitivity requirements for detecting EMRIs necessitate extremely stable and precise instruments, along with robust data analysis techniques to distinguish faint signals from noise.
Gravitational waveform models used in the detection and parameter estimation of extreme mass ratio inspirals (EMRIs) rely on calculations of geodesic motion in the black hole spacetime. Recent research indicates that the presence of a dark matter halo surrounding the black hole systematically shifts the radial location of epicyclic resonances, which are key features in the gravitational waveform. Specifically, these shifts result in quantifiable modifications to both the innermost stable circular orbit (ISCO) and the epicyclic frequencies – the frequencies at which a test particle orbits the black hole. Accurate modeling of these effects, including the magnitude and radial dependence of these shifts, is crucial for correctly interpreting observed gravitational wave signals and precisely determining black hole parameters, as well as characterizing the properties of the surrounding dark matter distribution.
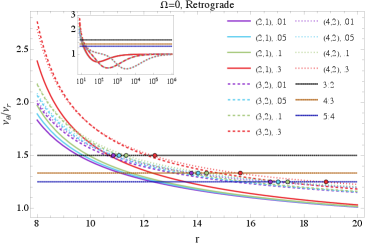
The study meticulously maps the distortions imposed by external matter on the spacetime around a rotating black hole. It’s a humbling exercise, revealing how even seemingly stable geometric descriptions are susceptible to environmental influence. This echoes Immanuel Kant’s assertion: “Two things fill me with ever new and increasing admiration and awe… the starry heavens above and the moral law within.” Just as the external universe shapes perception, so too does the surrounding matter-in this case, a dark matter halo-fundamentally alter the predictable behavior of spacetime. Any calculation of epicyclic frequencies, any prediction regarding gravitational waves, exists within this contingent reality, forever vulnerable to the consuming gravity of external factors.
The Horizon Beckons
The meticulous mapping of spacetime around slowly rotating black holes, even with the added complication of dark matter halos, feels less like progress and more like refining the instruments with which to chart an abyss. The current work, predictably, exposes the limitations of the slow rotation approximation – a pragmatic concession, certainly, but one that throws the more turbulent realities of astrophysics into sharper relief. It’s a comfortable exercise, applying the Einstein Field Equations, until one remembers the universe isn’t built on convenient symmetries. Physics is the art of guessing under cosmic pressure, and the pressure just increased.
The search for gravitational wave signatures from extreme mass-ratio inspirals, touted as a precision test of general relativity, may ultimately reveal not flaws in the theory itself, but the messy, irreducible complexity of the environments these events inhabit. A dark matter halo isn’t a neat parameter to be slotted into an equation; it’s a dynamical system in its own right. The subtle shifts in epicyclic frequencies – the very signals this research attempts to isolate – could just as easily be whispers of phenomena yet unknown, or the result of applying a model beyond its domain of validity.
One suspects the true challenge lies not in calculating increasingly precise orbits, but in accepting the inherent unknowability at the heart of the problem. A black hole doesn’t just swallow matter; it swallows information, and ultimately, theories. The elegant mathematics, the carefully constructed models… they all look pretty on paper until you look through a telescope. The horizon beckons, and it’s a remarkably effective editor.
Original article: https://arxiv.org/pdf/2602.10579.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- All Her Fault cast: Sarah Snook and Dakota Fanning star
- Ben Stiller’s Daughter Ella Details Battle With Anxiety and Depression
- Sister Wives’ Meri Brown Alleges Ex Kody Brown Asked Her to Sign a NDA
- Pokémon Legends: Z-A’s Mega Dimension Offers Level 100+ Threats, Launches on December 10th for $30
2026-02-12 18:19