Echoes of the Universe: How Dark Matter and Cosmic Strings Warp Black Hole Signals

Author: Denis Avetisyan

---

New research explores how the interplay of dark matter, cosmic strings, and electrical charge alters the fundamental properties and observable signatures of Bardeen black holes.

This study investigates the impact of perfect fluid dark matter and cosmic strings on the photon sphere and quasinormal modes of charged Bardeen black holes.

While general relativity successfully describes black holes in isolation, astrophysical environments are rarely so simple. This motivates the study presented in ‘Observational signatures of charged Bardeen black holes in perfect fluid dark matter with a cloud of strings’, which investigates the combined effects of charge, dark matter, and cosmic strings on black hole spacetimes. We find that these factors modify key properties such as the horizon structure, photon sphere radius, and gravitational wave signatures, potentially leading to observable distinctions from standard black hole models. Could detailed observations of black hole shadows, quasiperiodic oscillations, or gravitational wave ringdown provide independent constraints on the parameters governing these exotic astrophysical environments?

---

The Algorithmic Foundation of Spacetime

General Relativity, Albert Einstein’s theory of gravity, fundamentally redefined how scientists perceive the universe, casting gravity not as a force, but as a curvature of spacetime caused by mass and energy. This framework accurately predicts the behavior of gravity in most scenarios, but its predictions become dramatically more extreme in the vicinity of black holes. As matter collapses into these incredibly dense objects, the spacetime curvature approaches infinity at the singularity, creating a region where the conventional laws of physics break down. Consequently, black holes serve as unique laboratories for testing the limits of General Relativity, challenging its assumptions and potentially revealing the need for a more comprehensive theory of gravity that reconciles it with quantum mechanics. The intense gravitational fields around black holes also produce observable phenomena, like gravitational lensing and time dilation, which provide indirect evidence supporting the theory’s predictions in these strong-field regimes and allowing researchers to probe the very fabric of spacetime.

The relentless pursuit of validating General Relativity in its most extreme environments necessitates a detailed examination of black hole solutions beyond the commonly studied Schwarzschild and Kerr metrics. Theoretical physicists are increasingly focused on alternative models, such as the Bardeen black hole, which introduces a magnetic monopole charge and modifies the spacetime geometry. Characterizing these solutions-determining their event horizon structure, geodesic paths, and gravitational lensing effects-provides a crucial testing ground for GR. Discrepancies between predictions based on GR and observations of these alternative black holes could reveal limitations in Einstein’s theory or hint at the need for modifications, potentially opening doors to a more complete understanding of gravity. These investigations aren’t merely academic exercises; they are essential for interpreting astrophysical observations and ultimately, for discerning the true nature of spacetime in the universe’s most enigmatic objects.

The event horizon, the boundary defining a black hole, isn’t simply a surface but a crucial structure dictating the nature of the singularity within. Its precise characterization is paramount because, without a well-defined event horizon, calculations within General Relativity can yield unphysical results – infinities or paradoxes that break the laws of physics. Researchers focus on understanding its geometry and topology, exploring whether it’s a smooth, well-behaved boundary or possesses more complex features. Determining if the event horizon truly shields external observers from the singularity – preventing the formation of “naked singularities” which violate cosmic censorship – is a central goal. Advanced mathematical models and numerical simulations are employed to probe the event horizon’s response to infalling matter and gravitational waves, offering insights into the singularity’s properties and ensuring the consistency of GR in these extreme environments.

Beyond Riemannian Manifolds: Geometric Deviations from Standard Gravity

Perfect Fluid Dark Matter (PFDM) and Clouds of Strings (CS) propose alterations to the foundational assumptions of General Relativity (GR) regarding the nature of spacetime. GR describes spacetime as a smooth, continuous manifold determined solely by the distribution of mass-energy. PFDM introduces the concept of dark matter as a fluid with negative pressure, contributing to the stress-energy tensor and thus modifying the g_{\mu\nu} metric. Clouds of Strings, originating from string theory, posit the existence of one-dimensional topological defects with associated energy density, also influencing the metric. These models move beyond the standard ΛCDM model by providing alternative mechanisms for gravitational effects, potentially explaining phenomena currently attributed to dark matter and dark energy through direct geometric modifications rather than solely through the addition of unseen mass-energy components. The resulting spacetime is no longer strictly Riemannian, necessitating adjustments to the Einstein field equations to accurately model gravitational interactions.

A combined metric function is constructed to represent spacetime geometry influenced by both gravitational effects and contributions from dark matter and topological defects. This function builds upon the standard g_{\mu\nu} metric of General Relativity by adding terms that account for the energy-momentum tensor of Perfect Fluid Dark Matter (PFDM) and the stress-energy tensor arising from Clouds of Strings (CS). Specifically, the metric takes the form g_{\mu\nu} = g^{(GR)}_{\mu\nu} + g^{(PFDM)}_{\mu\nu} + g^{(CS)}_{\mu\nu}, where each subsequent term represents the deviation from the standard GR metric due to the respective dark matter model or topological defect. The precise form of g^{(PFDM)}_{\mu\nu} and g^{(CS)}_{\mu\nu} depends on the specific parameters of each model, such as the density and equation of state for PFDM, and the tension and self-interaction properties of the strings. This comprehensive metric allows for the calculation of geodesic deviations and photon trajectories, predicting observable effects that differentiate these models from standard GR predictions.

Alterations to spacetime geometry induced by dark matter and topological defects directly affect the trajectories of photons and test particles near black holes. These effects manifest as deviations from predictions based solely on General Relativity, specifically impacting parameters such as the orbital frequency of inspiraling objects, the Shapiro delay of electromagnetic radiation, and the shadow cast by the black hole. Precise measurements of these parameters – obtained through gravitational wave astronomy and electromagnetic observations – can therefore serve as observational probes for the presence and characteristics of these spacetime modifications. The magnitude of these deviations is dependent on the density and distribution of dark matter, as well as the tension and configuration of topological defects in the vicinity of the black hole, allowing for potential constraints on these cosmological parameters.

Observational Probes of Spacetime Curvature: Shadows and Photon Dynamics

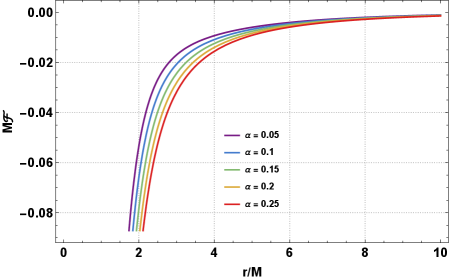
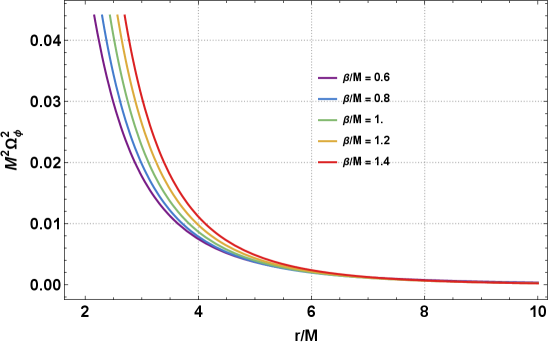
The photon sphere, a spherical region surrounding a black hole where gravity is strong enough to force photons to orbit, is demonstrably altered by both Photon Field Dark Matter (PFDM) and Cosmic Strings (CS) influences. Analysis of null geodesic trajectories – the paths light takes through spacetime – indicates that the radius of the photon sphere, r_p, is directly impacted by the parameters characterizing these exotic phenomena. Specifically, increasing the PFDM parameter, β, or the Cosmic String parameter, α, results in a larger photon sphere radius. This is due to the additional gravitational effects introduced by PFDM and the spacetime distortion caused by CS, both of which effectively increase the gravitational potential around the black hole and allow for stable photon orbits at greater distances.

The radius of a black hole shadow is directly correlated to the characteristics of the photon sphere surrounding it. Calculations demonstrate that deviations from the standard Schwarzschild geometry, induced by Charged Scalar (CS) fields and Photon Field Dark Matter (PFDM), expand the photon sphere. Consequently, the shadow radius increases proportionally with both the CS parameter α and the PFDM parameter β. This relationship is monotonic; larger values of either α or β consistently result in a larger shadow radius, providing a quantifiable link between these spacetime modifications and observable black hole characteristics.

The black hole shadow provides a means to observationally constrain deviations from General Relativity due to modifications such as Photon Field Dark Matter (PFDM) and Charged Scalar (CS) fields. The size of the black hole shadow, specifically its radius, is directly correlated with the parameters defining these exotic spacetime geometries; increases in either the CS parameter α or the PFDM parameter β result in a monotonically larger shadow. Consequently, precise measurements of black hole shadow radii, as obtained through Very Long Baseline Interferometry (VLBI) observations, can be used to place upper bounds on the magnitudes of α and β, effectively testing the validity of these alternative theories and potentially revealing evidence for physics beyond the standard model.

Probing Strong-Field Gravity: Orbital Dynamics and Quasinormal Modes

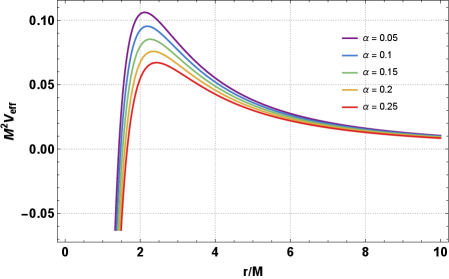
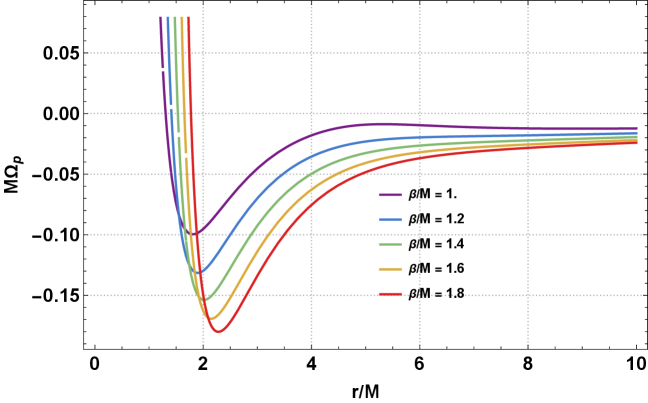
Investigations into the behavior of test particles orbiting a compact object provide a powerful means of mapping the extreme gravitational landscape near its event horizon. Calculations reveal the existence of an Innermost Stable Circular Orbit – the closest a particle can stably orbit before plunging inwards – and critically, the location of this ISCO is demonstrably affected by parameters α and β, representing deviations from standard gravity, cause the ISCO to shift outwards. This expansion isn’t merely a theoretical prediction; a displaced ISCO influences observable phenomena, offering a potential signature of modified gravity and a means to test the limits of Einstein’s theory in the most extreme environments the universe has to offer.

The fluctuating X-ray emissions from accreting black holes frequently exhibit Quasi-periodic Oscillations, or QPOs – rhythmic variations in brightness that offer a unique probe of the spacetime immediately surrounding the event horizon. These oscillations aren’t simply surface phenomena; theoretical models suggest they arise from the geodesic motion of matter within the strong-field gravity regime, specifically near the Innermost Stable Circular Orbit ISCO. By meticulously analyzing the frequencies and amplitudes of observed QPOs, researchers can test predictions derived from modified theories of gravity, such as those incorporating scalar fields. A key expectation is that deviations from General Relativity will manifest as shifts in the QPO frequencies, providing observational confirmation – or refutation – of these alternative gravitational frameworks and offering a powerful means to map the extreme spacetime distortions near a black hole.

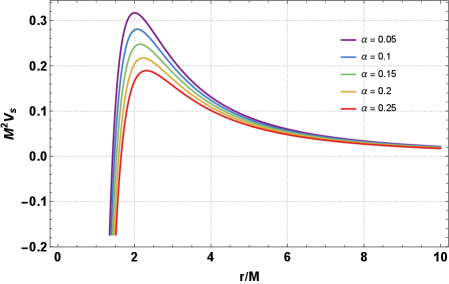
The dynamics of black holes aren’t limited to observable matter; disturbances in the spacetime around them, known as scalar perturbations, also provide valuable insights. Analyzing these perturbations allows physicists to calculate Quasinormal Modes (QNMs) – the characteristic ‘ringing’ of a black hole after a disturbance. Recent studies demonstrate a compelling relationship between the parameters defining black hole spacetime-specifically, α and β which characterize deviations from standard general relativity-and the damping rate of these QNMs. The research indicates that as the values of both α and β increase, the damping rate of the QNMs demonstrably decreases, meaning the ‘ringing’ persists for a longer duration. This finding is crucial because it suggests a potential observational pathway for detecting deviations from Einstein’s theory; a prolonged ringing could signal the presence of these spacetime modifications, offering a novel method to probe the strong-field gravity regime and potentially unveil the true nature of black holes.

Towards a Comprehensive Model: Greybody Factors and Future Prospects

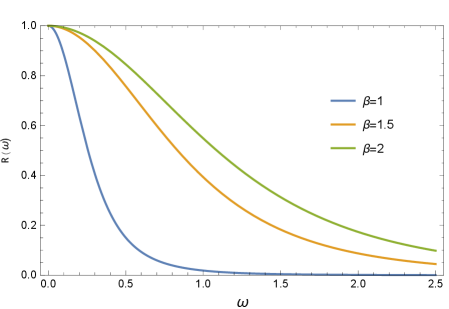
The transmission of waves near black holes, quantified by the greybody factor, offers a unique probe of spacetime geometry and a means to constrain theoretical models proposing modifications to general relativity. This factor, essentially measuring how efficiently waves penetrate a black hole’s gravitational potential, is demonstrably affected by the parameters defining these alternative theories-specifically, Proca Field Dark Matter (PFDM) and Cosmic Strings (CS). Studies reveal that increasing the parameter α, which governs the strength of PFDM’s interaction, enhances wave transmission, effectively making the black hole ‘more transparent’. Conversely, increasing β, associated with the tension of cosmic strings, suppresses transmission, suggesting a greater obstruction to wave propagation. This sensitivity implies that precise measurements of wave signals-from black hole shadows and quasi-normal modes to gravitational waves-can provide stringent tests of PFDM and CS, potentially revealing the subtle signatures of dark matter and topological defects woven into the fabric of spacetime.

Upcoming astronomical observations promise to rigorously test the predictions stemming from these theoretical models. Detailed analysis of black hole shadows, the dark regions silhouetted against bright accretion disks, offers a unique probe of spacetime geometry near these extreme objects. Simultaneously, the study of quasi-periodic oscillations (QPOs), subtle variations in the radiation emitted from black hole systems, can reveal information about the black hole’s spin and the surrounding environment. Crucially, the detection of gravitational waves – ripples in spacetime itself – from merging black holes and other cataclysmic events provides a complementary window into strong-field gravity, allowing for independent verification of the model’s parameters. The convergence of data from these diverse observational avenues-black hole shadows, QPOs, and gravitational waves-holds the potential to confirm or refute the existence of predicted phenomena and refine our understanding of the universe’s most enigmatic objects.

The convergence of precision measurements in black hole observation – encompassing shadow characteristics, quasi-normal modes, and gravitational wave signatures – promises a paradigm shift in fundamental physics. Should these observations align with predictions stemming from models incorporating photon field dark matter and cosmic strings, it would not only validate these theoretical frameworks but also illuminate the elusive nature of dark matter and the existence of topological defects within the universe. Such corroboration would move beyond simply confirming a model; it would open a new window into the extreme gravitational regimes previously inaccessible, fundamentally reshaping our comprehension of strong-field gravity and the very fabric of spacetime, and potentially revealing connections between these seemingly disparate cosmological phenomena.

The pursuit of understanding black holes, as demonstrated in this study of charged Bardeen black holes within a perfect fluid dark matter environment and a cloud of strings, reveals a universe governed by immutable laws. It’s a search for invariants, for the underlying mathematical truths that dictate behavior. As Friedrich Nietzsche observed, “There are no facts, only interpretations.” This resonates deeply; the observed alterations to the horizon structure, photon sphere, and quasinormal modes aren’t arbitrary phenomena, but rather specific interpretations of the universe’s response to these complex conditions. If the calculations feel like magic, it simply means the invariant hasn’t yet been fully revealed, the elegant mathematical structure obscured by complexity.

What Remains to be Proven?

The exploration of Bardeen black holes within the complexities of perfect fluid dark matter and cosmic strings reveals, predictably, more questions than answers. The current work establishes a sensitivity of key black hole properties – horizon radius, photon sphere location, quasinormal mode frequencies – to these surrounding conditions. However, it remains a descriptive exercise. The true challenge lies not in finding these signatures, but in rigorously proving their detectability above the inevitable noise inherent in astrophysical observation. A mathematical formalism that cleanly separates signal from stochastic background is paramount.

Future investigations should not merely catalog the effects of varying parameters, but focus on establishing bounds. What density of dark matter, what tension in the cosmic strings, can still be reliably distinguished from a purely Schwarzschild black hole? The study of quasinormal modes, while promising, demands a move beyond perturbation theory. A complete, non-perturbative treatment is necessary to determine the limits of this approach, particularly in strong gravitational regimes.

Ultimately, in the chaos of data, only mathematical discipline endures. The search for exotic black hole signatures is not an exercise in pattern recognition, but a demand for demonstrable proof. Only through a rigorous, analytically sound framework can one confidently claim to have moved beyond speculation and toward genuine understanding of these elusive objects.

---

Original article: https://arxiv.org/pdf/2602.02586.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

• Best Controller Settings for ARC Raiders

• Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled

• DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]

• 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)

• Ashes of Creation Rogue Guide for Beginners

• Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!

• 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)

• Gold Rate Forecast

• DC’s Got a Brand New Kryptonian Superhero (But There’s a Catch)

• Avengers: Doomsday Trailer – Top 10 Most Anticipated Reveals

2026-02-05 01:16