Author: Denis Avetisyan
New calculations reveal how quantum entanglement behaves in warped spacetime geometries, bridging the gap between gravity and quantum field theory.
This review details numerical computations of entanglement entropy and logarithmic negativity using techniques like the replica trick and heat kernel expansion in AdS and other curved backgrounds.
Quantifying entanglement in curved spacetime remains a formidable challenge, hindering a complete understanding of quantum field theory in gravitational backgrounds. This is addressed in ‘Numerical Computations of Entanglement Measures in Curved Space’, which presents novel numerical and analytical computations of entanglement entropy and logarithmic negativity for scalar and gauge fields in various spacetimes, including Anti-de Sitter spaces. Utilizing techniques like the replica trick, heat kernel expansion-and comparisons to results derived from heat kernel coefficients-the study explores connections between boundary conformal field theories and their bulk gravitational duals, providing insights into \mathcal{N}=4 super-Yang-Mills theory. How might these numerical approaches further illuminate the role of entanglement in the emergence of spacetime geometry and resolve outstanding questions regarding UV divergences and conformal anomalies?
Unveiling the Paradox: Entanglement and the Limits of Classical Intuition
Entanglement, a phenomenon where two or more particles become linked and share the same fate no matter how far apart they are, profoundly disrupts classical understandings of the universe. Traditional physics relies on the principle of locality – that an object is only directly influenced by its immediate surroundings – and assumes information cannot travel faster than light. However, entangled particles exhibit correlations that appear instantaneous, suggesting a connection beyond the constraints of spacetime. This isn’t simply a matter of missing information; the correlations violate Bell’s inequalities, demonstrating that these systems cannot be described by any local hidden-variable theory. Consequently, entanglement compels physicists to reconsider fundamental assumptions about the nature of reality, pushing the boundaries of how information and causality are perceived and demanding new theoretical frameworks to reconcile quantum mechanics with our intuitive grasp of the cosmos.
Quantifying the interconnectedness of quantum systems-specifically, calculating entanglement entropy-presents a significant hurdle for conventional quantum field theory. This measure, crucial for understanding quantum correlations, becomes computationally intractable as systems grow more complex. Traditional methods struggle because entanglement isn’t a local property; it demands considering correlations across vast distances, defying the localized calculations that quantum field theory typically performs. The sheer number of interacting particles in many-body systems exacerbates this difficulty, requiring exponential computational resources to accurately map these correlations. Consequently, researchers are actively developing novel theoretical frameworks and computational techniques-such as tensor networks and the replica trick-to circumvent these limitations and gain a clearer understanding of entanglement in realistic quantum materials and scenarios. S = -Tr(\rho log_2 \rho)
The calculation of entanglement entropy, a crucial metric for quantifying quantum correlations, faces significant hurdles due to the very nature of entanglement and the systems in which it manifests. Entanglement’s non-locality-the instantaneous correlation between particles regardless of distance-defies classical notions of spatial separation and introduces complexities that traditional quantum field theory struggles to accommodate. Moreover, real-world quantum systems are rarely isolated pairs; instead, they consist of many interacting bodies, each entangled with others. Describing the collective behavior of these many-body systems – where entanglement permeates the entire system rather than existing between just two particles – demands computational resources and theoretical frameworks that push the boundaries of current capabilities, necessitating innovative tools and approaches to fully unravel the mysteries of quantum correlation.
Harnessing Gravity: Holography and the Geometric Nature of Entanglement
The Anti-de Sitter/Conformal Field Theory (AdS/CFT) correspondence is a conjectured duality proposing that a gravitational theory defined in an n-dimensional Anti-de Sitter (AdS) space is equivalent to a conformal field theory (CFT) residing on the (n-1)-dimensional boundary of that space. This isn’t a statement of physical equivalence in the traditional sense, but rather a strong equivalence of their respective theories; observables in one theory correspond to observables in the other. AdS space is a maximally symmetric solution to Einstein’s equations with a negative cosmological constant, resulting in a spacetime with constant negative curvature. CFTs, conversely, are quantum field theories invariant under conformal transformations – transformations that preserve angles but not necessarily distances. The correspondence allows for calculations in the strongly coupled regime of the CFT, which are often intractable using conventional methods, by mapping them to calculations in the weakly coupled, classical gravity regime in AdS space.
The Ryu-Takayanagi (RT) formula, arising from the AdS/CFT correspondence, provides a geometric interpretation of entanglement entropy. Specifically, the entanglement entropy of a region A in the conformal field theory (CFT) is equivalent to the area of the minimal surface \gamma_A in the associated Anti-de Sitter (AdS) space, with the boundary of \gamma_A coinciding with the boundary of region A. This minimal surface, known as the RT surface, effectively calculates the number of degrees of freedom participating in the entanglement across the boundary of region A. The area is calculated using the induced metric on the surface, and represents a direct relationship between a geometric quantity in the bulk AdS space and a quantum information theoretic quantity in the boundary CFT.
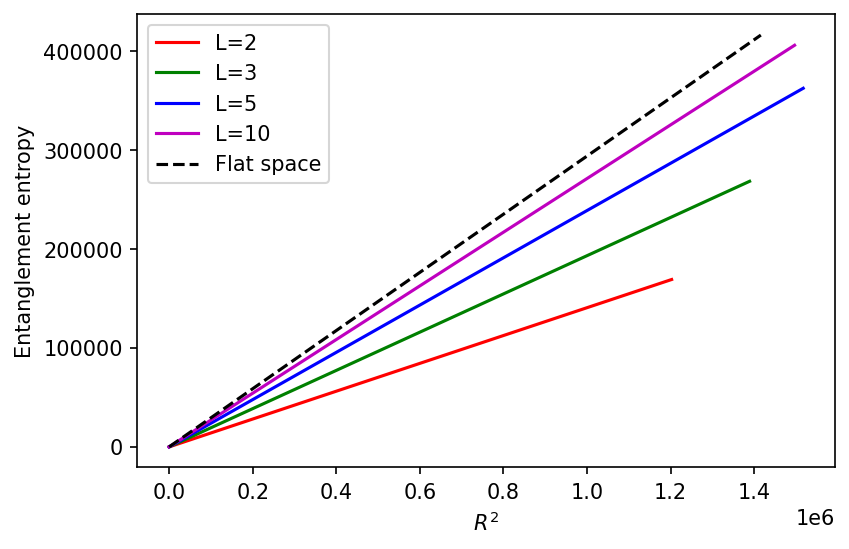
Precise calculations of minimal surfaces – known as RT surfaces – within Anti-de Sitter (AdS) space are facilitated by the use of coordinate systems such as Global AdS Coordinates. These calculations directly determine the entanglement entropy of the corresponding conformal field theory (CFT) residing on the AdS boundary. Empirical results demonstrate adherence to the expected area law, where entanglement entropy scales proportionally to the area of the RT surface. This relationship has been verified for both scalar and vector fields within AdS4 spacetime, and for calculations performed inside RT surfaces in the lower-dimensional AdS3 space; the observed proportionality constant confirms the theoretical predictions based on the AdS/CFT correspondence and \text{Area} = 2\pi G_N S.
Dissecting Correlation: Analytical and Numerical Approaches to Entanglement Entropy
The Replica Trick is an analytical technique used to compute entanglement entropy by establishing a direct relationship with Rényi entropy. This method involves analytically continuing the number of replicas, n, to a non-integer value, typically approaching zero, to obtain the entanglement entropy. Specifically, entanglement entropy, S, is expressed as the limit S = \lim_{n \to 1} \frac{1}{n-1} \log \text{Tr}(\rho^n), where ρ is the reduced density matrix of the subsystem. Calculating the trace involves computing the partition function of the replicated system, which is often more tractable than directly evaluating the entanglement entropy itself. The success of the Replica Trick relies on the ability to perform this analytical continuation and extract the relevant information from the replicated system’s properties.
The Heat Kernel Method provides a complementary analytical approach to calculating entanglement entropy by expressing it as a series expansion in terms of the heat kernel K(x,x'). This method relies on the short-distance expansion of the heat kernel, which allows the entanglement entropy to be written as a sum of terms involving derivatives of K(x,x') evaluated at the boundary of the region. Specifically, the entanglement entropy S can be expressed as S = \text{Tr}[\rho \log \rho], where ρ is the reduced density matrix, and the heat kernel expansion provides a means to approximate this trace through a series. This is particularly useful when direct calculation of the Renyi entropies, as used in the Replica Trick, becomes intractable due to geometric complexity.
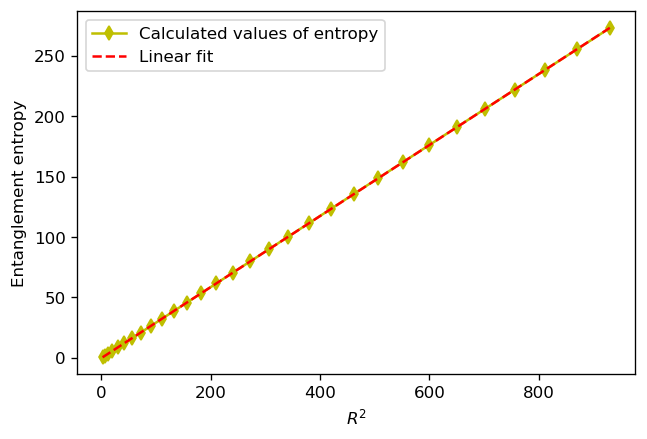
For geometries beyond those permitting analytical calculation of entanglement entropy – such as those with boundaries or lacking sufficient symmetry – numerical methods are essential. These techniques typically involve discretizing the relevant spacetime and approximating the necessary integrals. A common approach utilizes Proper Distance Coordinates, which provide a natural coordinate system adapted to the geometry and simplifies the calculation of geodesic distances – a key component in defining the entanglement region. The accuracy of these numerical calculations depends on the fineness of the discretization and the order of the approximation used, requiring careful consideration of computational cost and error control. Validation is often performed by comparing results to known analytical solutions in simplified cases or by confirming the expected behavior, such as the presence of the universal term -\frac{1}{90} for conformal fields.
Consistency between analytical and numerical calculations of entanglement entropy is demonstrated by the consistent emergence of a universal term in the entropy formula. For scalar fields in global AdS4 spacetime, these techniques yield a coefficient of -1/90 for this term. This value is significant as it precisely matches the established result for flat space entanglement entropy in the limit as the AdS radius, L, approaches infinity, thereby validating the methodologies used and reinforcing their applicability to diverse gravitational backgrounds and field theories.
Expanding the Horizon: Implications for Spacetime and Beyond
Investigations into the entanglement structure of cosmological horizons are advanced by applying established quantum information techniques to de Sitter (dS) spacetime, specifically utilizing the dS4 Static Patch Metric as a foundational model. This approach allows researchers to move beyond simply characterizing the area of these horizons and instead delve into the quantum correlations present across them. By examining entanglement within dS space, it becomes possible to explore the fundamental connection between quantum field theory and the accelerating expansion of the universe, offering insights into the nature of dark energy and the very fabric of spacetime. This methodology provides a crucial framework for understanding how quantum information is encoded and distributed in the context of cosmological event horizons, potentially revealing new principles governing the universe at its largest scales.
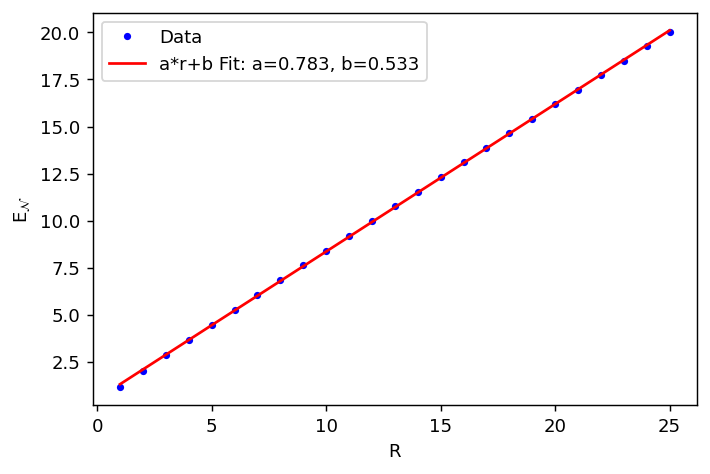
Beyond standard entropy measurements, characterizing quantum entanglement in expansive spacetime necessitates more nuanced tools, and Logarithmic Negativity provides precisely that refinement. This metric quantifies entanglement by focusing on the logarithmic derivative of the entanglement entropy, offering a more sensitive probe of quantum correlations, particularly in scenarios where entropy itself may be insufficient. Recent investigations reveal a compelling relationship between Logarithmic Negativity and spatial scale; for scalar fields within flat spacetime, this measure scales linearly with the radius R. This direct proportionality suggests that as the region under consideration expands, the degree of entanglement, as captured by Logarithmic Negativity, increases proportionally, providing a valuable insight into the fundamental connection between quantum correlations and the geometry of spacetime.
The analysis of quantum entanglement within spacetime relies heavily on mathematical techniques designed to dissect complex quantum states. Among these, the Schmidt Decomposition stands out as a pivotal tool, enabling researchers to express a bipartite quantum state – a state involving two entangled subsystems – in a simplified form. This decomposition identifies a set of orthogonal states, each associated with a specific entanglement contribution, allowing for the quantification of how strongly the two subsystems are correlated. By applying the Schmidt Decomposition, scientists can move beyond simply recognizing entanglement and begin to precisely measure its extent and structure, providing crucial insights into the fundamental relationship between quantum mechanics and the geometry of spacetime, particularly when studying cosmological horizons and the effects of quantum field theory on spacetime curvature. The resulting data reveals how entanglement isn’t merely a quantum property, but a feature deeply interwoven with the very fabric of reality.
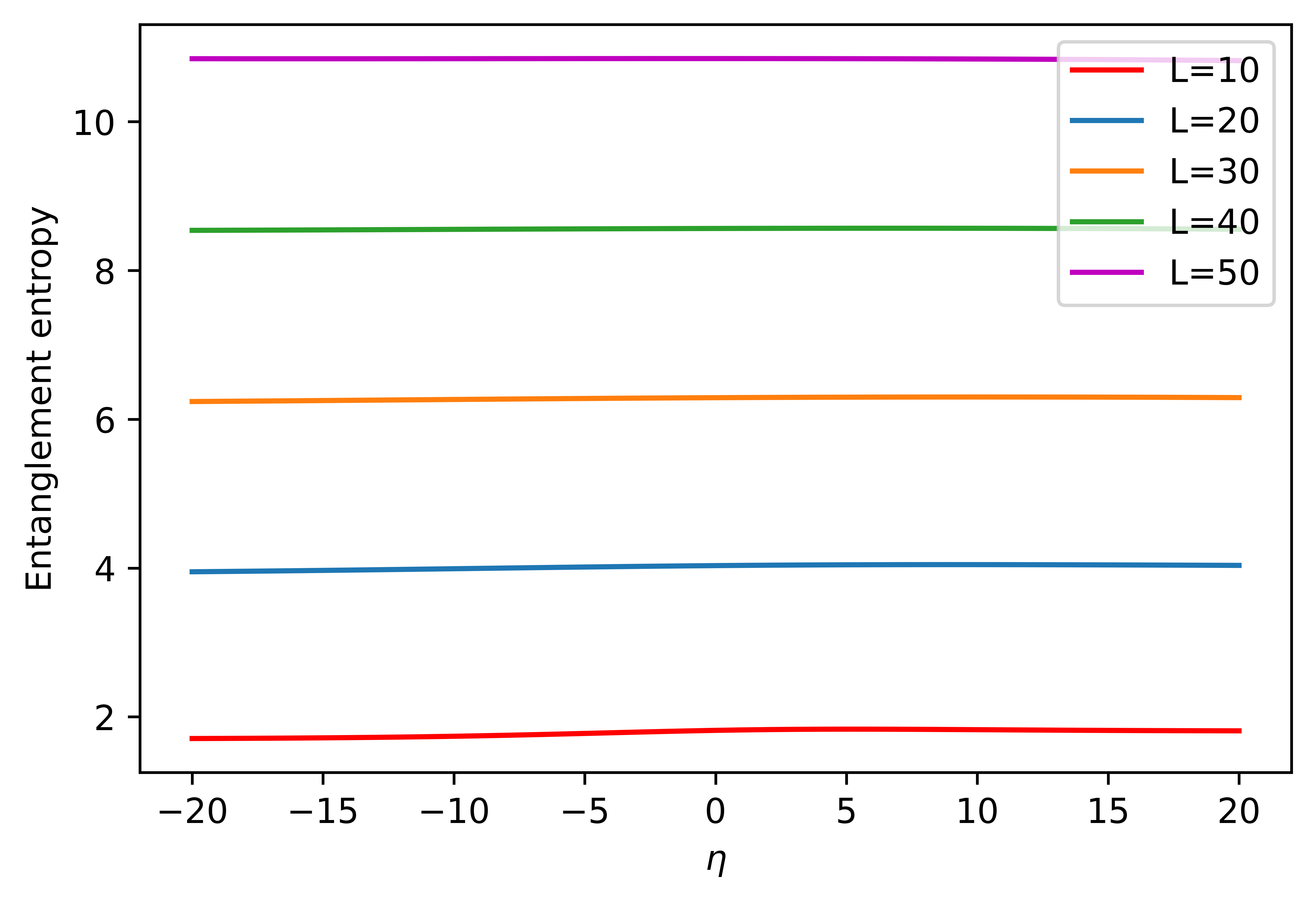
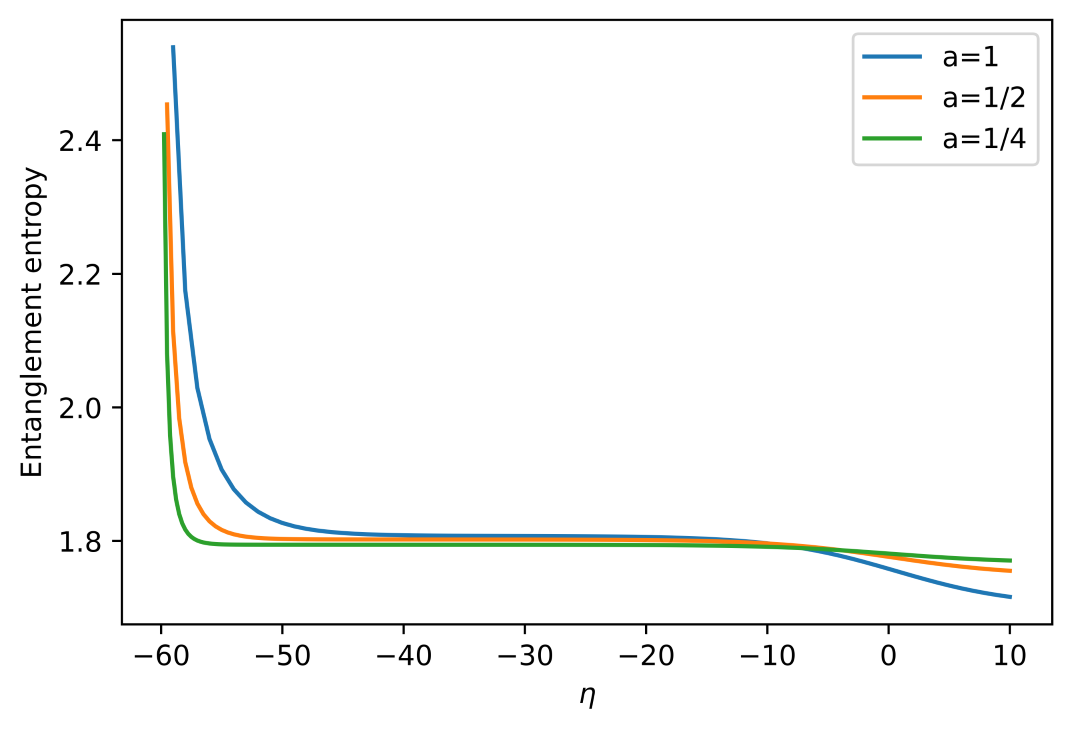
Investigations into the entanglement structure of spacetime reveal a surprising connection to the conformal anomaly, a phenomenon in quantum field theory that arises from the subtle interplay between symmetries and quantum effects. Calculations utilizing measures like Logarithmic Negativity – which quantifies entanglement beyond standard entropy – demonstrate that entanglement isn’t merely a property within spacetime, but is fundamentally linked to its geometry. Specifically, studies focusing on scalar fields within Ryu-Takayanagi (RT) surfaces in Anti-de Sitter space (AdS3) have shown that Logarithmic Negativity remains remarkably constant, independent of the time-like coordinate η. This suggests a deep relationship where the very act of tracing out degrees of freedom to calculate entanglement induces changes in the effective geometry, manifesting as the conformal anomaly and hinting at a holographic connection between quantum information and spacetime itself.
The pursuit of entanglement measures in curved spacetime, as detailed in this work, mirrors a fundamental principle of interconnectedness. Every calculation, every approximation – like the replica trick employed to navigate UV divergences – reveals how seemingly disparate parts of a system influence one another. This echoes Carl Sagan’s observation: “Somewhere, something incredible is waiting to be known”. The study’s exploration of AdS/CFT correspondence, linking boundary and bulk theories, highlights this holistic view; understanding the whole-the complete spacetime-is crucial, as structure dictates behavior. Simplifications, such as employing spherical harmonics, inevitably introduce trade-offs, yet contribute to a clearer understanding of the complex interplay between quantum fields and gravity.
Beyond the Horizon
The computations detailed herein, while providing valuable numerical corroboration of holographic principles, inevitably highlight the subtle architecture governing entanglement in curved spacetime. The persistent struggle with ultraviolet divergences is not merely a technical hurdle; it signals a deeper need to reconcile effective field theory with a truly complete understanding of quantum gravity. Addressing this necessitates moving beyond approximations, and perhaps accepting that the “bulk” is not simply a geometrical dual, but a fundamentally different manifestation of the same information.
Future work must grapple with the limitations inherent in relying on simplified spacetimes like AdS. Real astrophysical scenarios present far greater complexity, demanding new analytical tools and computational strategies. Furthermore, extending these calculations to excited states and time-dependent backgrounds will prove critical – a static spacetime tells only a partial story. The replica trick, though powerful, is not without its conceptual baggage, and alternative approaches to quantifying entanglement, less reliant on analytic continuation, deserve renewed attention.
Ultimately, this line of inquiry isn’t simply about calculating numbers; it’s about deciphering the underlying principles that connect quantum information and spacetime geometry. The persistent correspondence between boundary and bulk theories suggests a profound relationship, but a complete understanding will require embracing the full complexity of the system – recognizing that modifying one aspect of entanglement inevitably triggers a cascade of effects throughout the entire architecture.
Original article: https://arxiv.org/pdf/2601.21566.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Ashes of Creation Rogue Guide for Beginners
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Best Werewolf Movies (October 2025)
- 10 Ridley Scott Films With the Highest Audience Scores on Rotten Tomatoes
- All 6 Takopi’s Original Sin Episodes, Ranked
2026-01-31 08:24