Author: Denis Avetisyan
New research reveals the mechanics of entanglement in noisy quantum systems, identifying a characteristic velocity that governs how quickly information spreads.
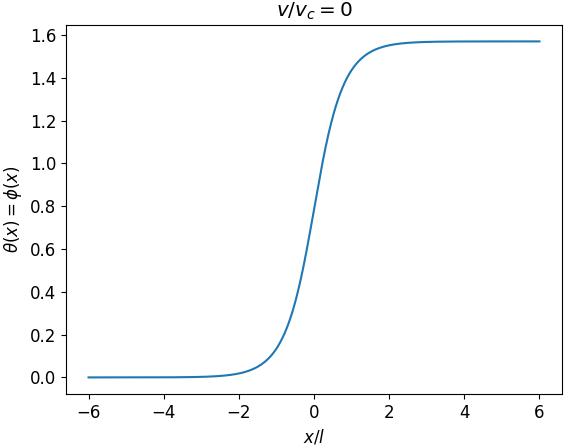
Analytical calculations demonstrate the emergence of an ‘entanglement membrane’ and determine the butterfly velocity in weakly interacting Majorana chains.
Understanding how quantum information scrambles in many-body systems remains a central challenge in modern physics. This is addressed in ‘Continuum mechanics of entanglement in noisy interacting fermion chains’, where we develop a continuum description of information propagation in weakly interacting Majorana fermion chains using a semiclassical approach based on the replica trick. Our analysis reveals the emergence of an ‘entanglement membrane’-a bound state of travelling waves-and demonstrates its unbinding as the membrane velocity approaches the butterfly velocity, signaling a transition to ballistic spreading. Can this continuum framework provide insights into the broader dynamics of entanglement and operator growth in more complex, disordered quantum systems?
Unveiling Entanglement’s Reach: A New Perspective on Quantum Dynamics
Characterizing the spread of quantum entanglement is fundamental to understanding the behavior of complex quantum many-body systems, yet directly observing this propagation presents a formidable scientific challenge. Entanglement, a uniquely quantum correlation linking particles regardless of distance, dictates the collective properties of these systems – from superconductivity to novel phases of matter – but its fragile nature and the sheer complexity of interacting particles make it incredibly difficult to track. Current observational techniques often struggle to capture the subtle, long-range correlations that define entanglement’s influence, particularly in systems where interactions are weak or disordered. Overcoming these limitations is crucial not only for advancing fundamental knowledge of quantum mechanics, but also for harnessing the power of quantum systems for technological applications like quantum computing and secure communication, where maintaining and controlling entanglement is paramount.
Characterizing quantum systems riddled with disorder presents a considerable hurdle for conventional analytical methods. These approaches typically rely on simplifying assumptions about uniformity and strong interactions, which break down when faced with the complexities of weakly interacting particles and long-range correlations. In disordered systems, the absence of a clear, repeating structure diminishes the effectiveness of techniques designed for periodic arrangements, while the subtle, extended influence of long-range correlations requires computational resources that rapidly become intractable. Consequently, understanding the behavior of these materials – increasingly relevant for advancements in quantum technologies – demands innovative theoretical frameworks capable of accurately capturing the delicate balance between disorder, weak interactions, and the far-reaching effects of quantum entanglement.
Researchers are focusing on weakly interacting Majorana chains as a means to chart the progression of quantum entanglement. These chains, comprised of quasiparticles known as Majoranas, hold significant potential for building robust topological quantum computers – devices less susceptible to environmental noise than conventional quantum systems. The unique properties of Majoranas – being their own antiparticles – facilitate the creation of entangled states that are inherently protected from local disturbances. By meticulously studying how entanglement spreads along these chains, scientists aim to gain insights into the fundamental behavior of many-body quantum systems and ultimately unlock the capabilities of fault-tolerant quantum computation. This investigation necessitates advanced theoretical models to accurately represent the complex interplay between interactions, disorder, and the propagation of entanglement within the Majorana chain.
Characterizing the spread of quantum entanglement in complex systems demands a sophisticated theoretical approach, particularly when dealing with weakly interacting and disordered materials. Existing models frequently falter when faced with the intricate relationships arising from these conditions. Consequently, researchers are developing new frameworks that go beyond traditional perturbation theories, employing techniques like bosonization and renormalization group methods to effectively capture the subtle dance between particle interactions and the randomness inherent in the material’s structure. This allows for a detailed examination of how entanglement-a crucial resource for quantum technologies-propagates through the system, revealing the critical factors that either enhance or suppress its spread and ultimately defining the material’s potential for quantum computation and information processing.
Mapping Entanglement: A Mathematical Toolkit for Quantum Systems
The replica trick is a mathematical technique used to calculate the Rényi entropy, a measure of entanglement, in many-body quantum systems. Directly computing entanglement entropy often requires knowledge of the full many-body wavefunction, which is computationally intractable. The replica trick circumvents this issue by considering n identical copies, or “replicas,” of the system and analyzing the correlation functions of identical particles across these replicas. This transformation effectively maps the problem onto a calculation of a partition function for n non-interacting particles, a statistically classical problem that is significantly easier to solve. The final entanglement entropy is then obtained by analytically continuing the result from integer n to n = 1.
The coherent state path integral provides a non-perturbative approach to quantum dynamics by representing the quantum mechanical propagator as a sum over all possible trajectories in phase space, weighted by a complex phase factor determined by the action. This formulation utilizes coherent states – quantum states that most closely resemble classical states – to map the quantum problem onto a classical-like integral. Specifically, the path integral expresses the transition amplitude between two states as \in t \mathcal{D}[q] e^{iS[q]} , where \mathcal{D}[q] represents the functional integral over all possible paths q(t) , and S[q] is the classical action. By employing coherent states, the functional integral becomes well-defined and amenable to analytical and numerical calculations, particularly advantageous when dealing with strongly correlated systems where traditional perturbative methods fail.
Calculating entanglement in many-body systems presents significant challenges due to the exponential growth of the Hilbert space with the number of particles. Traditional methods, such as direct diagonalization or perturbative approaches, quickly become intractable. The replica trick and coherent state path integrals offer a non-perturbative framework to address these complexities. These techniques allow for the mapping of entanglement calculations onto equivalent classical problems, circumventing the computational limitations associated with directly handling quantum states. This enables the extraction of quantitative measures of entanglement, such as Rényi entropies, and provides insights into the topological order and critical behavior of strongly correlated systems, which are inaccessible through conventional methods.
Traditional perturbative approaches to calculating entanglement in many-body systems often encounter difficulties due to the inherently non-local nature of entanglement and the exponential growth of required computational resources with system size. These methods rely on expanding physical quantities in terms of a small parameter, which breaks down when dealing with strongly correlated systems or large entanglement entropies. The replica trick, combined with coherent state path integrals, offers a non-perturbative framework that circumvents these limitations by reformulating the entanglement calculation as a classical problem involving the partition function of an auxiliary system. This allows for the computation of entanglement measures, such as the Rényi entropy, without being restricted by the convergence issues or computational complexity associated with perturbative expansions, particularly in regimes where strong correlations dominate.
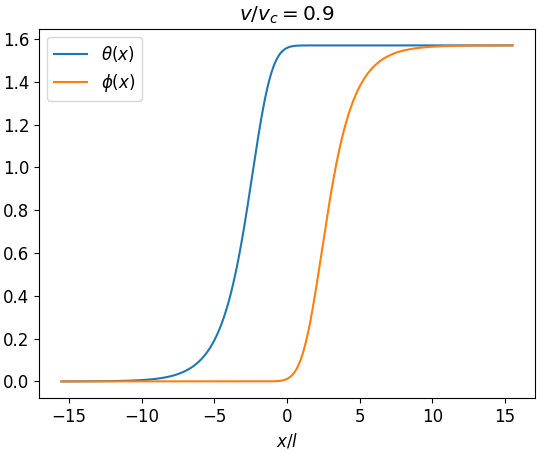
The Entanglement Membrane: A Wave-Like Description of Quantum Correlation
Application of the saddle-point approximation to the quantum mechanical path integral yields a direct correspondence with the Fisher-KPP equation, a well-established partial differential equation describing the propagation of travelling waves. The Fisher-KPP equation, originally formulated to model the spread of advantageous genes in a population, mathematically describes the evolution of a front separating two distinct states. In this context, the connection demonstrates that quantum information, specifically entanglement, can be modeled as a propagating wave phenomenon, with the solutions to the Fisher-KPP equation dictating the wave’s form and velocity. This analytical link allows for the application of techniques developed for studying travelling waves to understand the dynamics of entanglement propagation within the quantum system.
The application of the saddle-point approximation to the path integral formalism reveals that entanglement propagation can be modeled as a wave-like phenomenon. This leads to the conceptualization of an ‘entanglement membrane’ – a propagating front that demarcates the region of entangled versus non-entangled states within the system. This membrane isn’t a physical surface, but rather a mathematical construct describing the spatial extent of entanglement. The velocity of propagation for this membrane is not arbitrary, but is instead governed by system parameters, and its tension is directly related to that velocity, providing a quantifiable characteristic of entanglement spread. The emergent wave behavior offers a novel perspective on how entanglement disseminates and equilibrates throughout the system.
The emergent entanglement membrane exhibits a tension directly proportional to the velocity at which entanglement spreads through the system. This relationship allows for the characterization of entanglement propagation not simply as a diffusion process, but as wave-like motion with a defined velocity and associated mechanical properties. Specifically, the tension within this membrane is a function of the system’s velocity, offering a novel metric for quantifying the rate of entanglement spread and providing a connection between information transfer and effective ‘mechanical’ properties of the entangled state. This framework facilitates analysis of how quickly information can propagate given the established tension, offering a new approach to understanding and predicting entanglement dynamics.
Calculations utilizing the saddle-point approximation, corroborated by analysis of the Out-of-Time-Ordered Correlator (OTOC), demonstrate that entanglement propagation and subsequent equilibration are governed by a critical velocity, v_c = 16\sqrt{2}\Delta_0\Delta_I. This velocity represents the rate at which entanglement spreads through the system. The OTOC analysis confirms that deviations from this critical velocity result in either the attenuation or stagnation of entanglement propagation, indicating its fundamental role in determining the system’s entanglement dynamics. Specifically, the calculations show that entanglement propagates effectively only when the rate of spread approaches this calculated critical velocity.
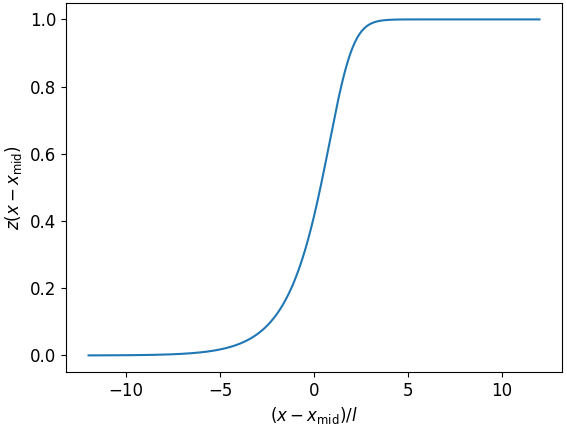
Unveiling the Limits of Information Velocity in Entangled Systems
The behavior of the entanglement membrane, a key feature in understanding quantum dynamics, is fundamentally governed by the ‘butterfly velocity’ – the speed at which minute disturbances propagate through the system. This velocity isn’t merely a characteristic of the membrane, but a critical parameter dictating its overall response to external influences and internal fluctuations. Investigations reveal that changes to this velocity directly impact the membrane’s structure and stability; slower propagation speeds correlate with a more robust, less susceptible membrane, while faster speeds indicate increased sensitivity and potential for disruption. Determining this velocity, therefore, is crucial for predicting and controlling the quantum system’s evolution, offering insights into how information is scrambled and restored within the entanglement membrane and potentially impacting the development of quantum technologies reliant on controlled entanglement.
The study reveals a fundamental connection between the speed at which small disturbances propagate – termed the ‘butterfly velocity’ – and a ‘critical velocity’ that demarcates shifts in the system’s dynamical behavior. Researchers determined this critical velocity to be precisely vc = 16\sqrt{2}\Delta_0\Delta_I, where \Delta_0 and \Delta_I represent key parameters characterizing the system. This finding establishes that the critical velocity isn’t simply a threshold, but an intrinsic property dictated by the system’s inherent ability to transmit information, thereby linking the speed of disturbance propagation directly to the transitions between different operational states.
Investigations into the entanglement membrane – a phenomenon arising from quantum entanglement – demonstrate a direct relationship between its internal tension and the speed at which disturbances propagate through it. Utilizing a Markov process to describe the Out-of-Time-Ordered Correlation (OTOC), researchers have established that the membrane’s tension scales linearly with this propagation velocity. This finding suggests that the membrane isn’t simply a static structure, but a dynamic entity where the rate of information transfer directly influences its structural integrity. Essentially, the faster disturbances travel, the greater the tension within the entanglement membrane, implying a fundamental connection between information velocity and the cohesive forces binding entangled quantum systems – a principle with implications for understanding emergent phenomena in complex quantum materials.
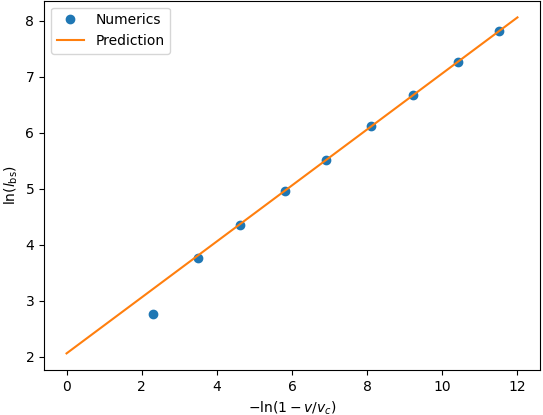
A universal scaling function, denoted as g(v/vc), dictates the behavior of the entanglement membrane, revealing a deep connection between information velocity and system dynamics. Analysis indicates that the size of the bound state within this membrane diverges as the velocity, v, approaches the critical velocity, vc, following the relationship lbs \sim 1/\sqrt{1 - |v|/vc}. This divergence signifies a critical point where the entanglement becomes unbound, dramatically altering the system’s properties. This finding establishes a novel theoretical framework for understanding how entanglement, information propagation, and critical phenomena are intrinsically linked in quantum systems, offering a powerful tool to predict and interpret the behavior of complex quantum matter near critical transitions.
The study illuminates how interconnectedness defines system behavior, much like a well-planned city. The emergence of the ‘entanglement membrane’-a boundary governing operator propagation-highlights that structure dictates function. As Aristotle observed, “The whole is greater than the sum of its parts.” This resonates with the analytical approach taken, demonstrating that understanding the collective dynamics of interacting Majorana chains-and the resulting butterfly velocity-requires consideration of the system as a unified entity, not merely isolated components. The infrastructure of entanglement, therefore, evolves without demanding a complete rebuild, mirroring the principles of robust, adaptable systems.
Beyond the Membrane
The analytical framework presented here, while illuminating the emergent entanglement membrane in weakly interacting Majorana chains, necessarily simplifies a reality rarely so obliging. The replica trick, a powerful tool, demands careful consideration of its limitations – the assumption of a well-defined large-n limit, for instance, may obscure subtle, yet crucial, deviations in strongly correlated systems. Future work must address the validity of this approximation and explore alternative analytical pathways for regimes beyond its reach.
The identification of the butterfly velocity as a fundamental speed limit for operator spreading is a compelling result, yet begs the question of its universality. Does this velocity – dictated by the chain’s microscopic parameters – truly represent a boundary for information propagation in all one-dimensional fermionic systems, or is it a specific consequence of the Majorana nature of the constituents? A rigorous investigation across different interaction strengths and system Hamiltonians is crucial to establish its broader applicability.
Ultimately, the structure revealed here suggests a fascinating interplay between entanglement, geometry, and dynamics. The emergent membrane, with its characteristic tension, hints at a deeper connection between quantum information and the effective spacetime arising within these chains. Perhaps the true path forward lies not in chasing ever-more-precise analytical solutions, but in embracing numerical methods capable of capturing the full complexity of these entangled systems, and probing the limits of this semiclassical approximation.
Original article: https://arxiv.org/pdf/2601.21134.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Ashes of Creation Rogue Guide for Beginners
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Donkey Kong Country Returns HD version 1.1.0 update now available, adds Dixie Kong and Switch 2 enhancements
- Emmerdale star Joshua Richards on Bear’s shocking descent into modern slavery – and past role exploring “horrifying” subject matter
- Arc Games is Now an Independent Game Publisher
2026-01-31 20:11