Faster Cooling in the Quantum Realm

by

Author: Denis Avetisyan

New research sheds light on how quantum systems can sometimes cool down faster than classical physics predicts, challenging our understanding of thermodynamics.

The quantum Mpemba effect demonstrates that, under specific conditions, a system initially in a mixed state can exhibit faster thermalization than one starting in a pure state, challenging classical intuition about heat transfer.
The quantum Mpemba effect demonstrates that, under specific conditions, a system initially in a mixed state can exhibit faster thermalization than one starting in a pure state, challenging classical intuition about heat transfer.

This review examines the mechanisms behind the Quantum Mpemba Effect in open quantum systems, focusing on the role of decoherence-free subspaces and non-Markovian dynamics.

The seemingly paradoxical phenomenon of faster relaxation to equilibrium in initially ‘hotter’ systems challenges conventional thermodynamic intuition. This is explored in ‘Unraveling the Quantum Mpemba Effect on Markovian Open Quantum Systems’, a study investigating the microscopic origins of the Quantum Mpemba Effect (QME) within open quantum systems. Our work demonstrates that exploiting decoherence-free subspaces and carefully engineering initial states can significantly accelerate relaxation, potentially leading to an extreme enhancement of decay rates towards equilibrium. Could these findings offer new pathways for manipulating and controlling the dynamics of complex quantum systems far from equilibrium?

Unveiling Counterintuitive Cooling: The Mpemba Effect

The Mpemba effect, a phenomenon defying everyday experience, suggests that under certain conditions, a warmer substance can freeze faster than a colder one. This counterintuitive observation, initially noted by Erasto Mpemba in 1963 while making ice cream, isn’t simply a matter of experimental error; repeated studies have confirmed its existence, though the precise mechanisms remain debated. The effect isn’t universal – it doesn’t occur with all substances or under all circumstances – and factors like convection currents, evaporation, and the presence of dissolved gases are thought to play crucial roles. While seemingly paradoxical given the second law of thermodynamics – which dictates heat flows from hot to cold – the Mpemba effect highlights the complexities of heat transfer and the importance of considering initial conditions and system-specific variables. Its continued study serves as a compelling reminder that even well-established physical principles can manifest in surprising and nuanced ways.

The observation that warmer water can, under certain conditions, freeze faster than colder water – a phenomenon known as the Mpemba effect – has captivated and challenged scientists for centuries. This counterintuitive behavior isn’t merely a curiosity for physicists; it has prompted extensive investigation across a surprisingly broad spectrum of disciplines. Initially explored within the framework of classical thermodynamics, attempts to explain the effect have drawn upon concepts like convection currents, supercooling, and the influence of dissolved gases. However, a purely thermodynamic explanation has remained elusive, leading researchers to consider the role of evaporation, heat transfer rates, and even the specific properties of the water itself. The enduring mystery has subsequently attracted attention from chemists examining isotopic variations, and mathematicians developing complex modeling to simulate the freezing process, demonstrating the Mpemba effect’s ability to serve as a unique testing ground for fundamental scientific principles.

Investigating the Mpemba effect within the framework of quantum mechanics reveals a landscape of possibilities far exceeding classical expectations. While the macroscopic phenomenon is already counterintuitive, its quantum analogue introduces complexities stemming from entanglement, superposition, and the non-classical nature of thermalization. Traditional thermodynamic tools prove inadequate for describing these scenarios, necessitating the development of new theoretical approaches – such as quantum kinetic equations and non-equilibrium Green’s functions – to accurately model heat transfer at the quantum level. Furthermore, the influence of quantum coherence and correlations on cooling rates becomes significant, potentially leading to scenarios where $quantum$ systems cool at rates dependent on their initial quantum state, rather than simply their temperature. This shift demands a re-evaluation of fundamental assumptions about thermal dynamics and opens avenues for exploring novel cooling technologies leveraging quantum phenomena.

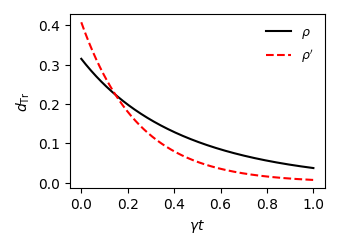
Simulations demonstrate that the quantum Mpemba effect occurs in this system, as the non-equilibrium free energy and trace distance for state ρ′ consistently decrease below those of state ρ after an initial period, given parameters ω=5, γ+=γ−=1, and T=10γ+ with an initial Bloch vector of 𝑹=(0.52807291,0.21585042,0.02214326).
Simulations demonstrate that the quantum Mpemba effect occurs in this system, as the non-equilibrium free energy and trace distance for state ρ′ consistently decrease below those of state ρ after an initial period, given parameters ω=5, γ+=γ−=1, and T=10γ+ with an initial Bloch vector of 𝑹=(0.52807291,0.21585042,0.02214326).

Modeling Open Quantum Systems: A Window into Accelerated Cooling

The quantum Mpemba effect, where a system can cool faster under certain conditions despite starting at a higher temperature, is not adequately explained by isolated quantum mechanics. Its behavior is best modeled as an open quantum system, meaning the system interacts with and is influenced by an external environment. This interaction introduces dissipation and decoherence, requiring a description beyond the closed system Schrödinger equation. The Markovian approximation, central to modeling these open systems, assumes the environment has no memory of the system’s past states; the current state of the environment is sufficient to determine its influence on the system’s dynamics. This simplification allows for a mathematically tractable description of the system’s evolution, capturing the essential features of the Mpemba effect as a consequence of environmental interactions and the resulting modification of the system’s energy levels and transition rates.

The Lindblad Equation, expressed as $d\rho = -i\mathcal{L}\rho dt$, provides a mathematically rigorous framework for modeling open quantum systems by describing the time evolution of the system’s density matrix, $\rho$. This equation incorporates the effects of environmental interactions through Lindblad operators, $L_k$, which represent the system’s coupling to its surroundings. These operators, when applied to the system’s initial state, account for dissipation and decoherence. The Liouvillian superoperator, $\mathcal{L}$, encapsulates both the system’s Hamiltonian and the effects of these environmental interactions, ensuring the resulting time evolution remains completely positive and trace-preserving – essential properties for a physically realistic quantum system. The Lindblad formalism allows for the calculation of reduced density matrices, effectively tracing out the environmental degrees of freedom and focusing on the system’s observable dynamics.

The Liouvillian superoperator, denoted by $\mathcal{L}$, is a key component in describing the time evolution of open quantum systems. It acts on the density matrix, $ \rho $, governing its change over time according to the equation $ \frac{d\rho}{dt} = \mathcal{L}\rho $. This operator encapsulates all possible transitions within the system and between the system and its environment. Specifically, $\mathcal{L}$ is a Hermitian operator, ensuring that the time evolution preserves the trace of the density matrix and maintains probabilistic consistency. Its eigenvalues determine the rates of decay or growth of different quantum states, and its eigenvectors represent the stationary states of the system under environmental influence. The Liouvillian formalism allows for a complete and consistent description of non-unitary dynamics in open quantum systems, moving beyond the limitations of the Schrödinger equation when external interactions are present.

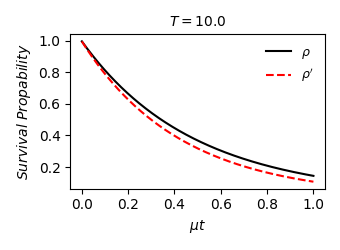
Trajectories reveal that the entropy of the state ρ′ increases more rapidly than that of ρ, contributing to its longer persistence in a mixed state, as evidenced by its higher survival probability and conditional non-equilibrium free energy.
Trajectories reveal that the entropy of the state ρ′ increases more rapidly than that of ρ, contributing to its longer persistence in a mixed state, as evidenced by its higher survival probability and conditional non-equilibrium free energy.

Decoding Quantum Cooling: Initial States and Dynamic Evolution

The quantum Mpemba effect, where a hot system cools faster than a cold one under specific conditions, is demonstrably influenced by the initial quantum state of the system. Coherent states, defined as eigenstates of the annihilation operator – effectively representing minimal uncertainty wavepackets – and squeezed vacuum states, which exhibit reduced noise in one quadrature at the expense of increased noise in the other, are particularly relevant. Simulations and theoretical analysis indicate that these non-classical states, when used as initial conditions, can lead to a more rapid decrease in internal energy – quantified by the system’s expectation value of the Hamiltonian – compared to systems initialized in thermal states. The effect stems from the altered dynamics of energy transfer and dissipation when the initial state deviates from thermal equilibrium, impacting the rate of decoherence and ultimately the cooling time. Specifically, the non-classical correlations present in these states can enhance the coupling to the thermal bath, accelerating the system’s relaxation towards equilibrium.

Representing the quantum system as a Bosonic Gaussian system allows for analytical tractability due to the complete characterization of all relevant system properties by first and second order moments. This simplification relies on the fact that Gaussian states remain Gaussian under Gaussian operations, and the system’s dynamics can be fully described by the time evolution of the $Covariance Matrix$, which encapsulates the variances and covariances of the system’s quadrature operators. Specifically, the $Covariance Matrix$ – a symmetric matrix representing the second-order correlations – uniquely defines the Gaussian state and its evolution under linear quantum operations, enabling efficient calculation of quantities like purity, entanglement, and ultimately, the dynamics relevant to the quantum Mpemba effect without requiring wave function reconstruction.

The Davies map represents a specific instance of completely positive, trace-preserving maps used to describe the dynamics of open quantum systems extending beyond the limitations of purely Markovian descriptions. It defines a quantum dynamical semigroup, ensuring the preservation of probabilities and allowing for the modeling of non-Markovian effects such as memory or correlations. Formally, the Davies map is constructed from a completely positive operator $L$ and a Hamiltonian $H$, resulting in a generator of the dynamics given by $ \mathcal{D}[\rho] = L\rho L^\dagger – \frac{1}{2} \{L^\dagger L, \rho\} $. This formalism is particularly useful in situations where the system interacts with an environment in a non-negligible manner, and the system’s state evolution is not solely determined by its current state, but also by its past history.

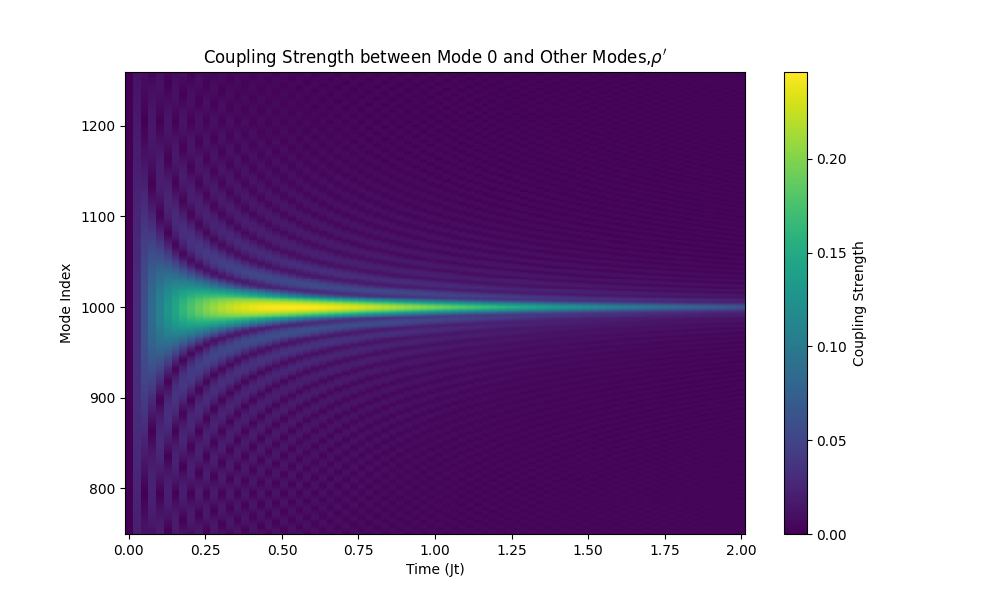
The non-equilibrium free energy and total correlation strength reveal distinct dynamics between coherent and squeezed vacuum states, as illustrated by the correlation dynamics between the system and each bath mode with α=1 and s=1.
The non-equilibrium free energy and total correlation strength reveal distinct dynamics between coherent and squeezed vacuum states, as illustrated by the correlation dynamics between the system and each bath mode with α=1 and s=1.

Quantifying the Effect: Metrics and Validation of Accelerated Cooling

The quantification of a system’s deviation from thermal equilibrium is crucial for understanding the quantum Mpemba effect, and the Non-Equilibrium Free Energy ($F_{NE}$) provides a robust metric for precisely that. This thermodynamic quantity doesn’t simply indicate whether a system is out of equilibrium, but rather how far it is from reaching a stable, balanced state. Researchers utilize $F_{NE}$ to map the conditions under which a hotter system can actually cool faster than a colder one – a counterintuitive phenomenon. A larger $F_{NE}$ value signals a greater disequilibrium, indicating a stronger potential for exhibiting the Mpemba effect. By carefully analyzing how $F_{NE}$ changes during the cooling process, scientists can pinpoint the specific parameters – such as initial temperature differences or system interactions – that maximize this accelerated cooling, offering valuable insight into the underlying mechanisms at play and validating theoretical predictions.

To rigorously compare the cooling rates of quantum systems experiencing the Mpemba effect, researchers employ the Trace Distance, a metric derived from the principles of quantum information theory. This measure quantifies the dissimilarity between two density matrices – mathematical representations of a system’s quantum state – allowing for a precise assessment of how different cooling trajectories diverge. A larger Trace Distance indicates a greater difference in the systems’ evolution, signifying a more pronounced Mpemba effect where one system cools faster than another despite starting from similar initial conditions. Essentially, the Trace Distance provides a quantifiable way to move beyond simple observation and establish the degree to which a system deviates from conventional thermal behavior, offering a robust tool for validating theoretical models and exploring the underlying mechanisms driving this counterintuitive phenomenon.

The quantum Mpemba effect, where a system cools faster under certain non-equilibrium conditions, is significantly bolstered by mechanisms such as collective decay and the presence of decoherence-free subspaces. Research indicates that these subspaces, which shield quantum information from environmental noise, dramatically accelerate relaxation times – exponentially faster than those observed in standard relaxation processes. Collective decay, where multiple quantum systems decay simultaneously, further enhances this effect by providing an additional pathway for energy dissipation. The existence of these mechanisms suggests that the observed acceleration in cooling isn’t merely a statistical anomaly, but rather a consequence of specific quantum pathways that facilitate more efficient energy transfer from the system to its surroundings, effectively reducing the time needed to reach thermal equilibrium and offering a potential route to manipulating quantum thermal processes.

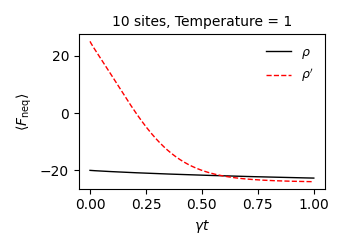
The non-equilibrium free energy exhibits distinct behaviors for the all-up state (red) and the decoherence-free subspace state (black) during evolution under collective dissipation at a temperature of Γ, with parameters set to Jz = 5, Γ = 1, and μ = 0.5.
The non-equilibrium free energy exhibits distinct behaviors for the all-up state (red) and the decoherence-free subspace state (black) during evolution under collective dissipation at a temperature of Γ, with parameters set to Jz = 5, Γ = 1, and μ = 0.5.

The exploration of accelerated relaxation, as detailed in the study of the Quantum Mpemba Effect, echoes a fundamental principle of pattern recognition. Just as discerning subtle visual cues requires a considered approach, understanding the QME demands careful manipulation of initial states and leveraging decoherence-free subspaces. As Erwin Schrödinger noted, “In spite of the fact that series of combinatorial flourishes are possible in every realm of knowledge, the ultimate touchstone is simplicity.” This simplicity isn’t about reducing complexity, but about identifying the underlying mechanisms-like exploiting non-Markovian dynamics-that govern a system’s evolution towards equilibrium. The research highlights that seemingly counterintuitive behaviors arise from specific arrangements, mirroring how a careful observer can reveal hidden patterns in complex data.

Where Do We Go From Here?

The demonstrated capacity to manipulate the Quantum Mpemba Effect (QME) via decoherence-free subspaces and initial state engineering reveals a peculiar truth: apparent violations of thermodynamic expectation are not necessarily contradictions, but rather manifestations of a system’s hidden structure. The current work suggests that the acceleration of relaxation is not simply a matter of initial conditions, but a consequence of effectively ‘shielding’ certain degrees of freedom from the usual disruptive influence of the environment. However, the limitations of Markovian dynamics remain a significant hurdle. Real quantum systems are rarely perfectly memoryless; the assumption of instantaneous decoherence simplifies the analysis but potentially obscures more subtle, non-Markovian mechanisms at play.

A natural progression of this research necessitates an exploration of the QME in systems exhibiting stronger environmental correlations. Can non-Markovian effects be harnessed to enhance or even reverse the observed acceleration? Furthermore, the present study focused on relatively simple open quantum systems. Extending these findings to many-body scenarios, where collective effects and emergent phenomena dominate, presents a formidable, yet potentially rewarding, challenge. The pursuit of the QME, it seems, is less about discovering a paradox and more about refining the boundaries of what constitutes ‘equilibrium’ itself.

Ultimately, the implications of this work extend beyond the realm of fundamental quantum mechanics. Understanding how to engineer accelerated relaxation – even in principle – could have unforeseen consequences for areas such as quantum information processing and the design of efficient energy transfer systems. The subtle interplay between coherence, decoherence, and environmental influence continues to offer a rich landscape for both theoretical inquiry and practical innovation.

Original article: https://arxiv.org/pdf/2512.13509.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-12-17 00:58