Fragile Coherence: How Asymmetry Reveals Quantum Order

Author: Denis Avetisyan

New research explores the delicate balance between quantum clustering and macroscopic coherence in spin chains following a localized disturbance.

The study reveals that asymmetry following a spin flip evolves predictably over time, with the rate of change-quantified as <span class="katex-eq" data-katex-display="false">\delta\mathcal{S}(\rho\_{A},Z\_{A})=(\Delta S(\rho\_{A},Z\_{A})-\Delta S\_{0})/\log t</span>-scaling consistently across varying subsystem sizes, suggesting a universal characteristic of this dynamic process. — The study reveals that asymmetry following a spin flip evolves predictably over time, with the rate of change-quantified as $\delta\mathcal{S}(\rho\_{A},Z\_{A})=(\Delta S(\rho\_{A},Z\_{A})-\Delta S\_{0})/\log t$ -scaling consistently across varying subsystem sizes, suggesting a universal characteristic of this dynamic process.

This study investigates the emergence of measurable coherence between charge sectors in the dual XXZ spin chain using tools like Quantum Fisher Information and Entanglement Asymmetry, extending the analysis to both integrable and non-integrable models.

Spontaneous symmetry breaking, while foundational in many-body physics, is inherently susceptible to perturbations that can disrupt long-range order and induce quantum coherence. This work, ‘Breaking of clustering and macroscopic coherence under the lens of asymmetry measures’, investigates the emergence of macroscopic quantum superpositions in a quenched $XXZ$ spin chain, focusing on the interplay between local interactions and the resulting non-equilibrium dynamics. We demonstrate that these dynamics generate measurable coherence between distinct charge sectors, effectively characterized by asymmetry measures such as Entanglement Asymmetry and Quantum Fisher Information, even within non-integrable models. Can these tools provide a universal framework for quantifying and understanding macroscopic quantum phenomena in increasingly complex systems?

The Fragile Equilibrium: Initiating the Quantum Disturbance

The behavior of complex quantum systems often deviates significantly from simple predictions, necessitating an understanding of their dynamics when removed from stable equilibrium. These systems, unlike those in perfect balance, respond to disturbances in fascinating and often unpredictable ways, requiring new theoretical approaches. A common method for initiating such non-equilibrium behavior is the ‘local quench’ – a targeted disruption of the system’s initial, lowest-energy state. This technique allows researchers to observe how quantum properties evolve over time, revealing emergent phenomena and providing crucial tests for theoretical models. By carefully analyzing the system’s response to these localized disturbances, scientists can gain insights into the fundamental laws governing quantum interactions and ultimately model increasingly complex systems with greater accuracy.

A carefully crafted disturbance to a quantum system’s most stable, ground state serves as a powerful lens through which previously hidden behaviors can emerge. This ‘quench’ – a sudden alteration of the system’s parameters – effectively ‘shakes’ the quantum landscape, exciting the system and allowing researchers to witness the fleeting, yet fundamental, processes that govern its evolution. By observing how the system relaxes from this artificially induced instability, scientists gain insights into phenomena like entanglement, symmetry breaking, and the formation of novel quantum phases. This approach doesn’t merely describe what a system does, but reveals how it responds to change, offering a dynamic view of quantum mechanics beyond static equilibrium.

To investigate non-equilibrium dynamics in systems undergoing symmetry breaking, researchers frequently utilize the DualXXZHamiltonian as a particularly versatile and robust model. This Hamiltonian, a modification of the standard XXZ model, allows for the exploration of quantum phenomena arising from localized disturbances – termed ‘quenches’ – by providing a framework where interactions can be finely tuned. The DualXXZHamiltonian’s strength lies in its ability to accurately represent systems where certain symmetries are broken, leading to interesting emergent behaviors such as domain formation and topological excitations. By studying how the system evolves after a quench within this model, scientists can gain valuable insights into the fundamental mechanisms governing the relaxation and thermalization processes in complex quantum systems, offering a pathway towards understanding real-world materials exhibiting similar properties.

Numerical diagonalization of the scattering phase, using a truncated Fourier representation with <span class="katex-eq" data-katex-display="false">|n|, |m| \leq 250</span>, demonstrates high precision (up to <span class="katex-eq" data-katex-display="false">10^{-8}</span>) for <span class="katex-eq" data-katex-display="false">\Delta = 0.8</span> and <span class="katex-eq" data-katex-display="false">\Delta = 1.2</span>, as evidenced by eigenvalues and the representation of initial scattering modes, with dashed lines indicating non-analytic momenta at <span class="katex-eq" data-katex-display="false">\pm \cos^{-1} \Delta</span>. — Numerical diagonalization of the scattering phase, using a truncated Fourier representation with $|n|, |m| \leq 250$ , demonstrates high precision (up to $10^{-8}$ ) for $\Delta = 0.8$ and $\Delta = 1.2$ , as evidenced by eigenvalues and the representation of initial scattering modes, with dashed lines indicating non-analytic momenta at $\pm \cos^{-1} \Delta$ .

Mapping the Quantum Landscape: Analytical Solutions to Dynamic Evolution

The Coordinate Bethe Ansatz (CBA) is employed as a method for determining the time-dependent behavior of a quantum system following a local quench – a sudden, localized perturbation. This technique maps the post-quench system onto a set of non-interacting particles, allowing for the calculation of time evolution operators via the solution of $\text{Bethe}$ equations. Specifically, the CBA constructs quasi-particle states that diagonalize the time-dependent Hamiltonian, enabling the computation of correlation functions and other observables as functions of time. The method’s power stems from its ability to provide exact, analytical solutions for systems where traditional perturbative approaches fail, particularly those exhibiting strong correlations.

Employing the DualXXZHamiltonian enables analytical determination of post-quench system dynamics by transforming the problem into a more tractable form. This Hamiltonian, derived from the original system, facilitates the calculation of time-evolved states without resorting to numerical simulations. Specifically, the DualXXZHamiltonian allows for the expression of correlation functions and expectation values in terms of Bethe ansatz solutions, providing precise, analytical predictions of the system’s behavior as it evolves in time following a localized perturbation; this is achieved through the mapping of operators and states between the original and dual representations of the Hamiltonian.

The Bethe equations are a set of algebraic equations used to determine the exact energy eigenstates and eigenvalues of the DualXXZHamiltonian. These equations arise from the requirement that the asymptotic behavior of the Bethe states satisfies specific boundary conditions, ensuring single-valuedness and proper normalization. Solving the Bethe equations yields a complete set of $\psi_E$ eigenstates, each corresponding to a specific energy eigenvalue $E$ . These eigenstates and eigenvalues are then directly employed in calculating the time evolution of the system following a local quench, providing analytical access to dynamic properties that would otherwise require computationally intensive methods.

$The magnetisation profile following a spin flip exhibits correlations that depend on the parameter Δ, converging to the asymptotic limit described by Eq. (19) and constrained by a maximal bound state velocity of <span class="katex-eq" data-katex-display="false">v^{B}_{max}=\min(1,1/(2\Delta))</span>.$

The magnetisation profile following a spin flip exhibits correlations that depend on the parameter Δ, converging to the asymptotic limit described by Eq. (19) and constrained by a maximal bound state velocity of

v^{B}_{max}=\min(1,1/(2\Delta))

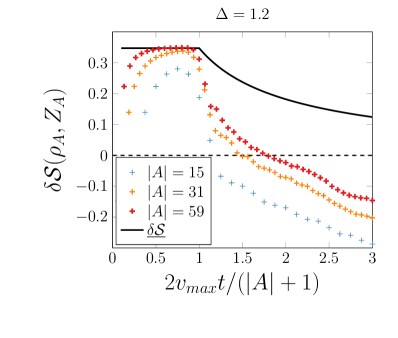
Decoding the Quantum State: Reduced Density Matrices as Observational Keys

The Reduced Density Matrix (RDM) provides a means of describing the quantum state of a subsystem by tracing out the degrees of freedom of the larger, composite system to which it belongs. This process effectively eliminates information about the environment, focusing solely on the relevant subsystem. Mathematically, if the total system is described by the density matrix ρ, and the subsystem of interest is described by the subspace A, the RDM $\rho_A$ is calculated as $\rho_A = Tr_B(\rho)$ , where $Tr_B$ denotes the partial trace over the degrees of freedom of subsystem B (the environment). The resulting RDM $\rho_A$ is a density matrix itself, completely characterizing the state of subsystem A, and is essential when dealing with systems where direct observation of the entire composite system is impractical or impossible.

Reduced Density Matrix (RDM) analysis provides a method for characterizing the quantum state of a subsystem by tracing out the degrees of freedom of the environment. This process yields a density matrix ρ that describes the subsystem’s state, revealing correlations and entanglement with the remaining system. Specifically, off-diagonal elements in ρ indicate quantum coherence and entanglement, while the eigenvalues of ρ represent the probabilities of observing the subsystem in specific eigenstates. By examining the structure of the RDM, researchers can quantify the degree to which the subsystem is entangled with, or correlated to, the larger system from which it was derived, providing insights into the overall quantum state without needing to fully characterize the entire system.

Entanglement Asymmetry, calculated from the Reduced Density Matrix $\rho_A$ , provides a quantitative measure of the degree to which a subsystem’s quantum state deviates from a classically separable state. Specifically, it assesses the imbalance in entanglement between the subsystem $A$ and its complement $B$ . A zero value indicates no entanglement, while a non-zero value signifies the presence of quantum correlations and superposition. Higher values of Entanglement Asymmetry correspond to a greater degree of quantum coherence and a stronger manifestation of non-classical behavior within the subsystem, indicating that the entanglement is not evenly distributed between the two partitions of the overall system.

The Quantum Fisher Information (QFI) is a metric quantifying a quantum state’s sensitivity to infinitesimal changes in a system parameter. Calculated from the Reduced Density Matrix (RDM), the QFI provides a lower bound on the precision with which that parameter can be estimated. A non-zero QFI value indicates the presence of persistent quantum fluctuations and confirms that the subsystem retains quantum mechanical properties despite being part of a larger, potentially decohering, system. Specifically, the QFI is calculated using the second derivative of the phase and is related to the Cramer-Rao bound; higher QFI values correspond to greater precision in parameter estimation and thus, stronger quantum fluctuations. $QFI = \langle \partial_{\theta} \psi | \partial_{\theta} \psi \rangle$ , where θ represents the parameter being estimated.

The time evolution of the reflected quantum Fisher information (rQFI) for subsystems of lengths 31 and 49, centered around the initial spin flip, aligns with analytical bounds <span class="katex-eq" data-katex-display="false">\eqref{65}</span>, while higher-order corrections <span class="katex-eq" data-katex-display="false">\eqref{68}</span>, <span class="katex-eq" data-katex-display="false">\eqref{69}</span>, and <span class="katex-eq" data-katex-display="false">\eqref{70}</span> provide further refinement. — The time evolution of the reflected quantum Fisher information (rQFI) for subsystems of lengths 31 and 49, centered around the initial spin flip, aligns with analytical bounds $\eqref{65}$ , while higher-order corrections $\eqref{68}$ , $\eqref{69}$ , and $\eqref{70}$ provide further refinement.

Revealing the Underlying Order: Scaling, Domain Walls, and the Nature of Symmetry

The application of the Scaling Limit provides a powerful methodology for dissecting the collective behavior of complex systems as they approach the thermodynamic limit – essentially, an infinitely large system size. This technique doesn’t focus on the specifics of individual components, but rather extracts the universal properties that emerge from their interactions. By effectively “zooming out” and disregarding microscopic details, researchers can identify fundamental characteristics – such as critical exponents and scaling functions – that govern the system’s behavior regardless of the material or precise conditions. This allows for broad generalizations and predictions about diverse physical systems, revealing underlying connections and simplifying the analysis of otherwise intractable problems. The Scaling Limit, therefore, acts as a lens through which the essential physics of a system can be revealed, independent of its particular realization.

The emergence of Domain Walls represents a crucial aspect of the system’s behavior following spontaneous symmetry breaking. These walls aren’t merely defects, but rather fundamental excitations – localized disruptions between regions of differing order. Their formation is a direct consequence of the system settling into a ground state that lacks the symmetry present in the initial Hamiltonian. Importantly, the density and behavior of these Domain Walls dictate many of the system’s macroscopic properties; they influence how quantum information is stored and propagated, and contribute significantly to the overall energy landscape. Studying these walls provides insight into the nature of the phase transition and reveals how local order emerges from a globally symmetric starting point, acting as the primary means by which the system organizes itself into a new, broken-symmetry state.

The emergence of domain walls – boundaries between regions of differing symmetry – is intricately connected to the system’s quantum properties. Investigations reveal a direct relationship between the behavior of these walls and measures of quantum entanglement, specifically entanglement asymmetry, which quantifies the imbalance of entanglement across the system. Crucially, the Quantum Fisher Information – a measure of sensitivity to infinitesimal changes in a quantum state – exhibits a non-zero value that scales proportionally with the system size. This indicates that the presence of domain walls enhances the system’s sensitivity to external perturbations and signifies the potential for increasingly precise measurements as the system grows, suggesting a fundamental link between symmetry-breaking, quantum information, and metrological precision within the studied phenomena.

Observations reveal a linear increase in transverse magnetization over time, a crucial indicator of macroscopic quantum superpositions within the system. This observation signifies that the system isn’t settling into a single, definite state, but exists as a combination of multiple states simultaneously – a hallmark of quantum mechanics typically observed at the microscopic level. The sustained, linear scaling suggests this superposition isn’t a transient phenomenon, but a stable, emergent property of the system’s collective behavior. This challenges classical intuition, where macroscopic objects are expected to possess definite properties, and points towards the realization of genuine quantum effects on a larger scale, potentially opening avenues for novel quantum technologies and a deeper understanding of the quantum-to-classical transition.

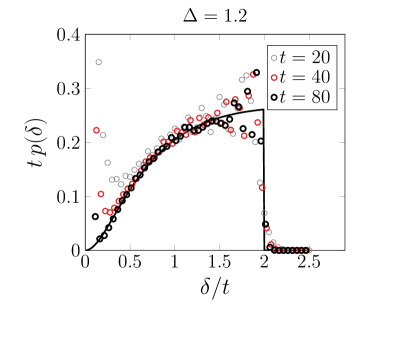
The probability of finding two domain walls separated by a distance δ is composed of a time-independent contribution from bound states and a scaling limit representing scattering states, as validated by comparison with the underlying continuous distribution.

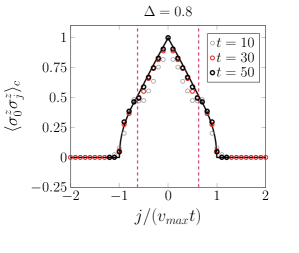
Tracing the Flow of Information: Correlations, Light Cones, and the Future of Quantum Dynamics

Analyzing correlation functions provides a detailed map of interconnectedness within the system following a sudden change, known as a quench. These functions quantify how much the state of one part of the system influences another, revealing a network of relationships that extends and evolves over time. By calculating these functions for various spatial separations, researchers can reconstruct the way information propagates – how disturbances or signals travel through the system. A strong correlation indicates a significant link, suggesting that the two parts are entangled or strongly interacting, while a weak correlation implies a more distant or independent relationship. The resulting correlation map is therefore crucial for understanding the system’s collective behavior and its response to external perturbations, providing insights into emergent phenomena and long-range order.

Reduced Density Matrix (RDM) analysis reveals that the correlations arising within a quenched system are not simply a snapshot of initial conditions, but are deeply shaped by the system’s inherent scaling limit and its dynamic response to the sudden change. The scaling limit, essentially how the system behaves at large distances or long times, dictates the form of these correlations – whether they exhibit power-law decay, exponential suppression, or more complex behavior. Simultaneously, the specific manner in which the system reacts to the quench – whether it equilibrates rapidly or oscillates for an extended period – significantly alters the spatial and temporal structure of these correlations. Consequently, understanding both the system’s fundamental scaling properties and its post-quench dynamics is crucial for interpreting the observed correlation patterns and discerning the underlying physics driving the system’s evolution. $RDM$ analysis, therefore, provides a powerful lens through which to investigate the interplay between static properties and dynamic responses in correlated quantum systems.

The extent of interactions within a quantum system following a rapid change, or ‘quench’, isn’t instantaneous; instead, information propagation is fundamentally limited by what is known as the LightCone. This concept, borrowed from relativity, dictates that no influence can travel faster than the maximum speed allowed within the system – effectively creating a boundary beyond which correlations cannot form. Imagine a disturbance at a single point; the LightCone visualizes the furthest reach of that disturbance over time. Consequently, measurements of correlations between distant parts of the system will only show significant relationships if those parts lie within this expanding cone, with correlations diminishing rapidly outside it. The shape and expansion rate of the LightCone, therefore, directly constrain the spatial and temporal extent of any observed entanglement or mutual information, providing a crucial tool for understanding how information disseminates and structures itself in the wake of a quantum event.

Observations reveal that the Quantum Fisher Information, a measure of sensitivity to infinitesimal changes in a quantum state, diminishes over time following a characteristic $1/t$ decay. This rate of decay signifies a gradual loss of quantum coherence within the system; as the Quantum Fisher Information decreases, the ability to precisely determine the system’s parameters-and therefore its quantum nature-is correspondingly reduced. This isn’t merely a loss of signal, but a fundamental erosion of the quantum correlations that define the system’s unique behavior, suggesting a transition towards a more classical state as time progresses. The proportionality to $1/t$ indicates this loss isn’t abrupt, but a slow, persistent fading of quantum information, providing insight into the system’s long-term dynamics and eventual thermalization.

The study of asymmetry measures in quantum systems, as demonstrated by this work on the dual XXZ spin chain, reveals a humbling truth about the limits of theoretical constructs. It echoes Hannah Arendt’s observation that “the extreme in its essence-corruption, evil, worldliness-has a disturbing quality: it wants to appear reasonable.” Just as models attempt to rationalize the complex behavior of quantum systems, they are perpetually vulnerable to the unforeseen – the breakdown of coherence, the emergence of domain walls, or the transition from integrable to non-integrable regimes. The paper’s exploration of macroscopic quantum superpositions and their sensitivity to asymmetry serves as a reminder that even the most rigorous mathematical framework can only approximate reality, susceptible to vanishing beyond the event horizon of true complexity.

What Lies Beyond the Horizon?

The demonstrated persistence of macroscopic coherence in the dual XXZ spin chain, even amidst the complexities of non-integrable perturbations, suggests a fragility in the very notion of objective reality as it pertains to quantum systems. Current quantum gravity theories suggest that inside the event horizon – here, the emergent domain walls separating charge sectors – spacetime ceases to have classical structure. The measurable asymmetries, quantified through tools such as Quantum Fisher Information, may then be less a description of physical properties and more an artifact of the observer’s limited access to information.

It is crucial to acknowledge that everything discussed remains mathematically rigorous but experimentally unverified. Future investigations must address the limitations of the Bethe Ansatz, particularly its applicability to genuinely chaotic systems. The scaling limit, while providing valuable insights, may obscure crucial details relevant to physical observation. Furthermore, a rigorous examination of the decoherence rates induced by realistic environmental interactions is essential, lest the observed coherence prove to be an idealized construct.

Perhaps the most pressing question concerns the universality of these findings. Do these entanglement asymmetries represent a fundamental property of quantum systems undergoing local quenches, or are they specific to the chosen model? The answer, it is suspected, will not illuminate the universe, but rather reveal the boundaries of the questions that can be meaningfully asked.

Original article: https://arxiv.org/pdf/2602.15969.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/