Author: Denis Avetisyan
New research explores how the transition between confined and deconfined states of matter relates to the breaking of chiral symmetry using a unique holographic model.
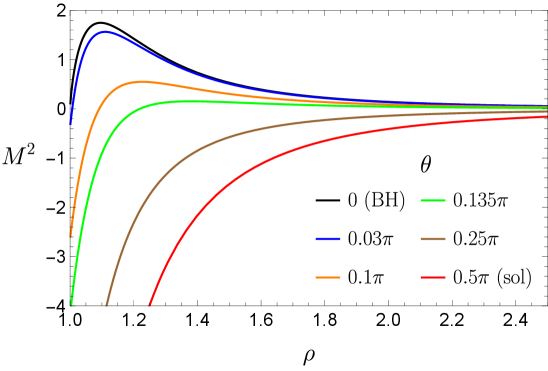
A holographic geometry smoothly interpolating between confined and deconfined phases reveals a simultaneous switch-off of confinement and chiral symmetry breaking linked to the expectation value of a stress-energy tensor component.
The interplay between confinement and chiral symmetry breaking-fundamental aspects of quantum chromodynamics-remains a central challenge in understanding strongly coupled systems. This paper, ‘Confinement and chiral symmetry breaking in holography: a smooth switch-off’, utilizes the holographic principle to explore this relationship in \mathcal{N}=4 super Yang-Mills theory compactified on a circle, revealing a continuous deformation connecting confined and deconfined phases. We demonstrate that both confinement and chiral symmetry breaking transition smoothly and simultaneously, linked to changes in the stress-energy tensor, and providing insight into the large N_c limit. Does this holographic framework offer a pathway to a more complete understanding of these phenomena in realistic hadronic systems?
The Geometry of Interaction: Unveiling Strong Coupling
Theoretical physics frequently encounters systems where interactions are so intense – termed ‘strongly coupled’ – that conventional approximation techniques, known as perturbative methods, simply fail. These methods rely on treating interactions as small disturbances, allowing for iterative calculations; however, when interactions dominate, these calculations produce meaningless results, like infinite values or diverging series. This poses a significant hurdle in understanding phenomena ranging from the quark-gluon plasma created in heavy-ion collisions to the behavior of high-temperature superconductors. The challenge isn’t merely computational; it’s fundamentally about a breakdown in the very tools used to describe the physics, necessitating entirely new theoretical frameworks capable of tackling these intractable systems and revealing their underlying principles.
The AdS/CFT correspondence, a cornerstone of modern theoretical physics, proposes a remarkable duality: a quantum field theory residing on the boundary of a space is fundamentally equivalent to a theory of gravity in one higher dimension – specifically, Anti-de Sitter (AdS) space. This isn’t merely an analogy, but a claim of complete equivalence, suggesting that all calculations performed in one theory have a corresponding counterpart in the other. Crucially, this framework offers a way to tackle strongly coupled quantum field theories, systems where traditional perturbative methods break down. By translating problems in the complex quantum realm to the more tractable domain of classical gravity, physicists can leverage geometric insights and analytical tools previously unavailable. The power of this duality lies in its ability to provide non-perturbative access to phenomena in quantum field theory, offering a novel approach to understanding everything from the quark-gluon plasma to the behavior of black holes.
The remarkable AdS/CFT correspondence provides a unique lens through which to examine N=4 Supersymmetric Yang-Mills (SYM) theory, a notoriously complex quantum field theory governed by strong interactions. Because direct calculation within N=4 SYM is often intractable, physicists leverage this duality to translate problems in the strongly coupled gauge theory into calculations within a weakly coupled gravitational theory residing in Anti-de Sitter (AdS) space. This gravitational “dual” effectively offers a classical, geometric description of the quantum behavior of N=4 SYM, allowing for insights into phenomena like quark-gluon plasma and the behavior of matter under extreme conditions. By studying the gravitational side, researchers can indirectly probe the strongly coupled dynamics of N=4 SYM – a feat impossible using traditional perturbative techniques applied directly to the gauge theory. This approach has not only deepened understanding of theoretical physics but also opened avenues for exploring potential connections between gravity and quantum information theory.
Phase Transitions: Mapping Geometry to Thermodynamics
At low temperatures, the system exists in a confining phase where the vacuum state is represented by a Soliton Geometry. This geometry is characterized by finite-size, localized solutions to the classical field equations, effectively creating a potential that confines the system’s constituent particles. The Soliton Geometry implies the existence of a non-perturbative mass gap, meaning that even in the vacuum, there is a minimum energy scale preventing particle dissociation. This contrasts with the deconfined phase and is mathematically described by solutions exhibiting topological stability, preventing decay into trivial configurations. The resulting energy density is finite and localized, defining a distinct ground state for the system.
At elevated temperatures, the system transitions to a deconfined phase characterized by a Black Hole Geometry. This phase is defined by the presence of a horizon, analogous to that of a black hole, which fundamentally alters the topological structure of the space. Unlike the Soliton Geometry of the confining phase, the Black Hole Geometry allows for the dissociation of fundamental constituents, leading to a state where particles are no longer bound. The formation of this geometry is a direct consequence of increased thermal energy overcoming the forces responsible for confinement, resulting in a state with greater entropy and a fundamentally different vacuum expectation value. R_s = 2GM/c^2 represents the Schwarzschild radius defining the event horizon in this deconfined state, where G is the gravitational constant, M is the mass, and c is the speed of light.
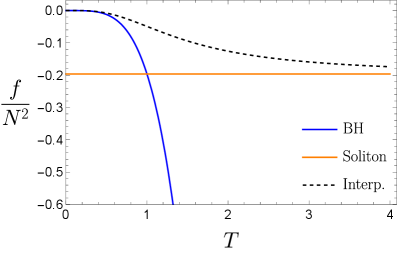
The thermodynamic stability of both the confining Soliton Geometry and the deconfined Black Hole Geometry is governed by the principle of minimizing the Free Energy F = E - TS, where E represents the energy, T is the temperature, and S is the entropy. Calculations demonstrate that at lower temperatures, the Soliton Geometry exhibits a lower Free Energy, thus representing the stable vacuum state. Conversely, as temperature increases, the Black Hole Geometry becomes energetically favored, minimizing the Free Energy and becoming the dominant phase. This transition occurs because the contribution of the entropy term TS to the Free Energy increases with temperature, ultimately outweighing the energy difference and driving the system towards the deconfined state. Therefore, the temperature-dependent minimization of Free Energy quantitatively determines which geometry represents the stable equilibrium configuration.
The system’s phase-either confining or deconfining-is directly correlated with temperature, exhibiting a continuous transition between the two states. As temperature increases, the system moves from a confining phase, characterized by Soliton Geometry, to a deconfined phase represented by Black Hole Geometry. This transition is not abrupt; rather, a smooth interpolation between the geometries occurs, indicating a second-order phase transition. The specific temperature at which the transition occurs is determined by minimizing the Free Energy of the system, with the geometry corresponding to the lowest free energy being the thermodynamically favored phase at that temperature. This demonstrates that temperature acts as the primary control parameter governing the system’s macroscopic behavior and the resulting geometric structure of the vacuum.
Confinement and String Tension: Probing the Quantum Vacuum
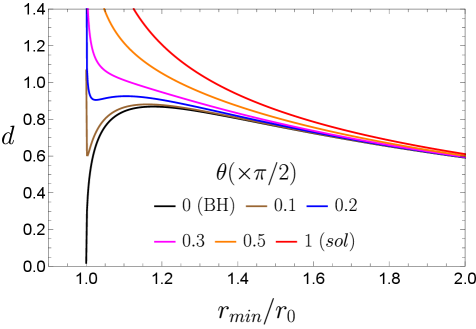
String tension, denoted as σ, directly quantifies the force experienced between static color charges – specifically, quarks – within a confining gauge theory. This parameter represents the force per unit length of a flux tube connecting the quarks, arising from the self-interaction of the gluon field. A non-zero string tension indicates confinement, meaning quarks are unable to exist in isolation due to the increasing energy required to separate them. Its value is determined by examining the potential energy V(r)[latex] between the static quarks, which at large distances typically exhibits a linear behavior: [latex]V(r) \approx \sigma r, where r is the separation distance. Consequently, string tension serves as a critical order parameter for the confinement/deconfinement transition in non-Abelian gauge theories like Quantum Chromodynamics (QCD).
The Wilson Loop, denoted as W = Tr(P \exp(i \oint_C A_\mu dx^\mu)), provides a method for calculating the static quark-antiquark potential. Here, A_\mu represents the gauge field, the integral is performed around a closed loop C, and the trace is taken over the color representation. Because the Wilson Loop is gauge-invariant, it is physically meaningful and independent of the specific gauge choice. The expectation value of the Wilson Loop, \langle W \rangle, is directly related to the static potential V(r)[latex] via [latex]\langle W \rangle = e^{-V(r)}, where r is the distance between the quarks. Therefore, analyzing the behavior of the Wilson Loop allows for quantitative determination of the confining potential and, consequently, the string tension, which quantifies the force experienced by the static quarks.
Calculations reveal that the string tension, a measure of the force between static quarks, is zero at zero temperature when the system is on the unstable branch of its phase diagram. This indicates a transition from a linear confining potential - where the force between quarks increases linearly with distance - to a screened state where the force diminishes exponentially. This behavior is quantified by observing the vanishing of the confining potential at large distances, implying that color charges are no longer confined but can be effectively screened by the surrounding medium. The precise value of the string tension, \sqrt{\sigma}, is directly related to the slope of the confining potential, and its disappearance signals the loss of confinement on this branch.
The string tension, a measure of the force between static quarks, is demonstrably affected by the phase of the system, specifically whether it exists in a Soliton or Black Hole phase. Calculations reveal a direct correlation between the geometric properties of these phases - including the horizon structure of the Black Hole phase and the topological features of the Soliton phase - and the resulting value of the string tension. A change in geometry, such as transitioning between these phases, leads to a measurable shift in the confining potential and therefore the string tension; this establishes a concrete link between the spacetime geometry and the phenomenon of quark confinement, indicating that confinement is not merely a dynamical effect but is intrinsically tied to the underlying geometric structure of the system. \sigma = F/r, where σ is the string tension, F the force, and r the distance between quarks, changes accordingly.
Chiral Symmetry and the Vacuum Structure: Unveiling the Origins of Mass
The generation of mass for fundamental particles like quarks isn't an inherent property, but rather emerges from a phenomenon known as chiral symmetry breaking. Initially, the equations describing these particles suggest they should be massless, yet experiments reveal they demonstrably possess mass. This discrepancy arises because the vacuum - seemingly empty space - isn’t truly empty, but instead possesses a complex structure that interacts with these particles. This interaction spontaneously breaks the chiral symmetry, a fundamental symmetry of the strong force, effectively giving quarks a mass through their interaction with this vacuum structure. This process is vital for understanding the stability of matter as massless quarks would preclude the formation of protons, neutrons, and ultimately, atoms. Consequently, chiral symmetry breaking is a cornerstone of modern particle physics, offering crucial insights into the strong force and the very fabric of reality.
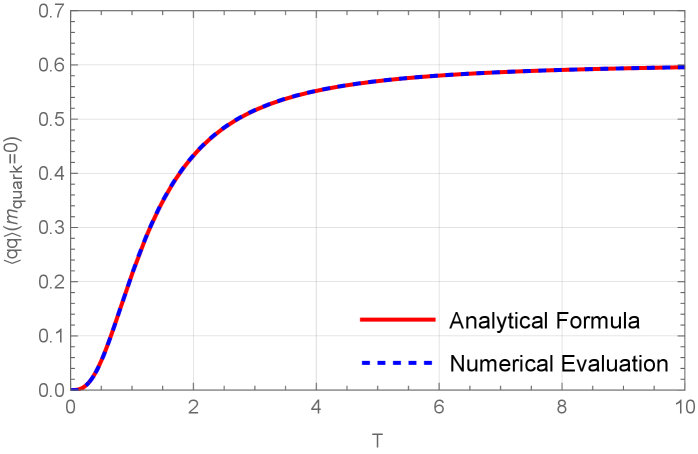
To investigate the origins of quark mass, a holographic model incorporating a D5-brane was constructed; this brane serves as a representation of quarks within a higher-dimensional spacetime. By analyzing the resulting Quark Condensate - a measure of quark-antiquark pairs in the vacuum - researchers aimed to simulate the behavior of these fundamental particles. The condensate’s value directly reflects the strength of interactions and the degree to which chiral symmetry is broken, a crucial process in generating mass. Detailed calculations reveal how the condensate forms and evolves under changing conditions, providing insights into the complex dynamics governing quark behavior and the structure of the vacuum itself. This approach allows for a theoretical exploration of phenomena inaccessible through conventional methods, bridging the gap between quantum field theory and gravity.
The emergence of a Quark Condensate serves as a key indicator of spontaneous chiral symmetry breaking, a phenomenon central to understanding how quarks acquire mass. This condensate, representing a non-zero vacuum expectation value for quark-antiquark pairs, aligns with established theoretical predictions derived from holographic models. Importantly, the strength of this condensate isn't static; it demonstrably decreases as temperature or density increases, ultimately vanishing at a critical point known as the deconfined endpoint. This behavior suggests a smooth transition from the chirally broken phase, where quarks are effectively massive, to a deconfined phase where they behave as nearly massless particles, offering valuable insight into the nature of matter under extreme conditions and the interplay between symmetry and confinement in quantum chromodynamics. The continuous decrease and eventual disappearance of the condensate provides a robust signal for this phase transition within the holographic framework.
Analysis of the Stress-Energy Tensor within the holographic model reveals a significant density of magnetic monopoles, suggesting a deep connection between the seemingly disparate phenomena of chiral symmetry breaking and quark confinement. This finding indicates that the mechanism responsible for giving mass to quarks - chiral symmetry breaking - may be intrinsically linked to the forces that hold them together within hadrons. Crucially, the study demonstrates a precise correspondence in scaling behavior between the Quark Condensate - a direct measure of chiral symmetry breaking - and the String Tension, which quantifies the strength of the confining force. This matching of scaling laws provides compelling evidence that both effects are facets of the same underlying physics, potentially offering a unified description of how mass and confinement emerge in quantum chromodynamics.
The pursuit of understanding complex phenomena, as demonstrated in this exploration of confinement and chiral symmetry breaking, benefits from elegantly constructed models. This work, detailing a smooth transition between confined and deconfined phases via holographic geometry, exemplifies how simplifying assumptions can illuminate fundamental connections. It echoes René Descartes’ assertion that “it is not enough to have a good mind; the main thing is to apply it well.” The paper’s construction of a one-parameter family of geometries, linking the switch-off of confinement and chiral symmetry breaking to the stress-energy tensor, is a testament to this principle - a carefully applied mind revealing deeper truths about the interplay of these forces.
Beyond the Horizon
The construction presented here, a smoothly interpolated geometry linking confined and deconfined phases, offers more than a technical achievement. It is a testament to the power of holographic duality to render complex phenomena amenable to geometrical intuition. Yet, the ease with which confinement and chiral symmetry breaking switch off together hints at a deeper underlying simplicity, perhaps even a certain… economy. One cannot help but wonder if this simultaneous vanishing isn’t merely a feature of the specific model chosen, but a constraint imposed by the very nature of these phenomena.
Future work must address the limitations of this approach. The precise relationship between the expectation value of the stress-energy tensor component and the transition remains somewhat opaque. Further refinement of the holographic dictionary-the translation between gravitational quantities and their field theory counterparts-is clearly needed. More importantly, explorations beyond the strictly static geometries presented here are crucial. A dynamic understanding of the transition-how it unfolds in real time-may reveal subtle but significant deviations from the observed smoothness.
Ultimately, this work serves as an invitation. An invitation to explore the landscape of holographic dualities with a more critical eye, seeking not just quantitative agreement, but qualitative elegance. For in the end, a truly insightful model should not merely describe the universe, but explain its inherent symmetries and constraints - and do so with a minimum of unnecessary complexity.
Original article: https://arxiv.org/pdf/2601.11136.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Darkwood Trunk Location in Hytale
- How To Watch A Knight Of The Seven Kingdoms Online And Stream The Game Of Thrones Spinoff From Anywhere
- Best Controller Settings for ARC Raiders
- Ashes of Creation Rogue Guide for Beginners
- Hytale: Upgrade All Workbenches to Max Level, Materials Guide
- Olympian Katie Ledecky Details Her Gold Medal-Winning Training Regimen
- PS5’s Biggest Game Has Not Released Yet, PlayStation Boss Teases
- RHOBH’s Jennifer Tilly Reacts to Sutton Stracke “Snapping” at Her
- Daredevil Is Entering a New Era With a Chilling New Villain (And We Have A First Look) (Exclusive)
- Shonda Rhimes’ Daughters Make Rare Appearance at Bridgerton Premiere
2026-01-20 23:17