Graphene’s Strange Response to Light Could Unlock New Physics

Author: Denis Avetisyan

A new theoretical study delves into the unusual dielectric properties of graphene, revealing unexpected behavior that could resolve inconsistencies in fundamental calculations.

The frequency-dependent response of graphene’s dielectric function demonstrates a clear threshold at <span class="katex-eq" data-katex-display="false">\omega = v_F q</span>, beyond which the material’s imaginary component-and thus its capacity to absorb energy-shifts dramatically, suggesting an inherent limit to its optical properties at a given momentum transfer of <span class="katex-eq" data-katex-display="false">q = 100~\mbox{cm}^{-1}</span> and temperature of 300K. — The frequency-dependent response of graphene’s dielectric function demonstrates a clear threshold at $\omega = v_F q$ , beyond which the material’s imaginary component-and thus its capacity to absorb energy-shifts dramatically, suggesting an inherent limit to its optical properties at a given momentum transfer of $q = 100~\mbox{cm}^{-1}$ and temperature of 300K.

This review investigates the quantum field theory of graphene’s dielectric function, highlighting a double pole at zero frequency with implications for the Casimir effect and evanescent wave interactions.

Discrepancies between theoretical predictions and experimental observations often arise when modeling the electromagnetic response of novel materials. This is addressed in ‘Quantum Theory and Unusual Dielectric Functions of Graphene’, which investigates the spatially nonlocal dielectric functions of graphene using thermal quantum field theory. The study reveals an unusual double pole at zero frequency within the material’s transverse dielectric function, potentially resolving long-standing puzzles like the Casimir effect disagreement. Could a similar, spatially nonlocal dielectric response with a double pole structure also be present in other metals, offering a more complete understanding of light-matter interactions at nanoscale dimensions?

The Fragility of Prediction: Graphene’s Quantum Signature

Graphene, a single-atom-thick sheet of carbon, exhibits remarkable electronic and optical characteristics stemming directly from its two-dimensional structure. This extreme thinness confines electron movement to just two dimensions, leading to unusually high electron mobility and unique light-matter interactions. Consequently, traditional theoretical frameworks-often designed for three-dimensional materials-prove inadequate for accurately predicting graphene’s behavior. A precise theoretical description requires accounting for quantum confinement effects and the resulting changes to its electronic band structure, influencing everything from its conductivity to its absorption of light. The material’s response isn’t simply a scaled-down version of bulk carbon; instead, it presents fundamentally new physical phenomena demanding sophisticated modeling techniques to fully unlock its potential in next-generation technologies.

The functionality of nanoscale devices increasingly relies on the unique electromagnetic properties of graphene, necessitating highly accurate theoretical modeling of its response to external fields. Because graphene exists as a two-dimensional material, its interaction with light and other electromagnetic radiation differs significantly from bulk materials; even subtle inaccuracies in these models can lead to substantial discrepancies between predicted and observed device performance. Precise modeling is crucial for optimizing designs for applications such as high-speed transistors, sensitive detectors, and novel plasmonic devices, where the manipulation of electromagnetic fields at the nanoscale is paramount. Consequently, researchers are continually refining computational techniques and theoretical frameworks to capture the complex interplay between graphene’s electronic structure and incident electromagnetic waves, ultimately enabling the full realization of its technological potential.

Current theoretical frameworks designed to predict graphene’s electromagnetic behavior increasingly diverge from experimental results, a discrepancy most pronounced when examining near-field phenomena – interactions occurring at distances comparable to or smaller than the wavelength of light. This challenge stems from the material’s unique two-dimensional structure and the highly localized nature of these near-field interactions, which demand an exceptionally accurate accounting of electron correlations and edge effects. Standard perturbative methods, while effective for bulk materials, often fail to capture the complex interplay of these factors in graphene, leading to inaccurate predictions of its optical and electronic response at the nanoscale. Consequently, researchers are actively exploring more sophisticated theoretical models, including non-perturbative approaches and advanced numerical simulations, to bridge the gap between theoretical predictions and observed experimental behavior, and unlock the full potential of graphene in advanced devices.

Graphene’s interaction with light is fundamentally governed by its dielectric function, a complex material property that describes how the material responds to an electromagnetic field. This function isn’t simply a constant; it’s frequency-dependent and intricately linked to graphene’s unique electronic band structure. A precise understanding of this dielectric function-including both its real and imaginary components-is crucial for predicting how graphene will absorb, reflect, transmit, and refract light at various wavelengths. Researchers are continually refining models of graphene’s dielectric function to account for factors like electron scattering, many-body effects, and the influence of external stimuli. Accurate modeling allows for the design of advanced optoelectronic devices, from high-speed photodetectors to ultra-sensitive sensors, and provides insights into near-field phenomena where light interacts with graphene at the nanoscale, demanding a theoretical treatment beyond conventional optics.

The longitudinal dielectric function of graphene exhibits a frequency-dependent response, peaking at <span class="katex-eq" data-katex-display="false">\omega = v_F q</span>, as illustrated for a temperature of 300K and a wavevector of <span class="katex-eq" data-katex-display="false">100~\mbox{cm}^{-1}</span>. — The longitudinal dielectric function of graphene exhibits a frequency-dependent response, peaking at $\omega = v_F q$ , as illustrated for a temperature of 300K and a wavevector of $100~\mbox{cm}^{-1}$ .

First Principles: The Illusion of Control

Quantum Field Theory (QFT) enables the calculation of material properties by treating particles as excitations of underlying quantum fields, rather than as fundamental entities. This approach allows for a description of many-body interactions with a well-defined mathematical formalism, moving beyond approximations inherent in single-particle models. Calculations begin with a Lagrangian describing the fields and their interactions, from which physical observables, such as energy levels, conductivity, and optical properties, can be derived using perturbation theory and other analytical or numerical techniques. The “first principles” designation indicates that these calculations rely only on fundamental constants and symmetries, without empirical parameters adjusted to fit experimental data, providing a predictive capability for novel materials and conditions. $\mathcal{L}[φ, ∂_μφ]$ represents a typical Lagrangian density used in QFT calculations.

The dielectric function of graphene, which quantifies its response to electromagnetic fields, can be rigorously determined using Quantum Field Theory (QFT). Unlike approaches relying on the random phase approximation or tight-binding models, QFT calculations account for many-body interactions and vacuum polarization effects. Specifically, QFT allows for the calculation of the $\Pi_{ij}(\mathbf{q}, \omega)$ polarization tensor, representing the induced dipole moment per unit volume in response to an applied field with wavevector $\mathbf{q}$ and frequency ω. This tensor directly relates to the dielectric function $\epsilon(\mathbf{q}, \omega)$ via $\epsilon_{ij}(\mathbf{q}, \omega) = \delta_{ij} + \frac{1}{\epsilon_0}\Pi_{ij}(\mathbf{q}, \omega)$ , where $\epsilon_0$ is the vacuum permittivity. The resulting dielectric function accurately predicts graphene’s optical properties, including its unique absorption characteristics and plasmonic behavior, going beyond the limitations of single-particle approximations.

Traditional material modeling often employs approximations, such as treating electron interactions as simple pairwise interactions or neglecting many-body effects. Quantum Field Theory (QFT) offers a framework to move beyond these limitations by explicitly accounting for the complex interplay between electrons and the electromagnetic field. This involves treating electrons not as individual particles, but as excitations of a quantum field, allowing for the inclusion of virtual particle exchange and correlation effects. Consequently, QFT-based calculations can accurately describe phenomena like many-body renormalizations and collective excitations, which are crucial for understanding material properties but are inaccessible to simplified models. The ability to model these intricate interactions is particularly important for materials with strong electron correlations, such as graphene and other 2D materials, where electron-electron interactions significantly influence their behavior.

The dielectric function, a fundamental property characterizing a material’s interaction with electromagnetic fields, is calculated by determining its polarization tensor. This tensor, a rank-two tensor, mathematically describes how a material responds to an applied electric field $\mathbf{E}$ . Each component of the polarization tensor relates the induced dipole moment per unit volume $\mathbf{P}$ to a specific component of the electric field: $\mathbf{P} = \epsilon_0 \chi \mathbf{E}$ , where χ represents the electric susceptibility and $\epsilon_0$ is the vacuum permittivity. Accurate determination of the polarization tensor requires accounting for the material’s electronic structure and the complex interactions between electrons and the applied field, including effects like electron correlation and many-body interactions.

The imaginary part of graphene’s longitudinal dielectric function, plotted logarithmically against frequency at 300K and <span class="katex-eq" data-katex-display="false">q = 100 \, \text{cm}^{-1}</span>, exhibits a threshold at <span class="katex-eq" data-katex-display="false">\omega = v_F q</span>. — The imaginary part of graphene’s longitudinal dielectric function, plotted logarithmically against frequency at 300K and $q = 100 \, \text{cm}^{-1}$ , exhibits a threshold at $\omega = v_F q$ .

Revealing the Signature: Validating the Prediction

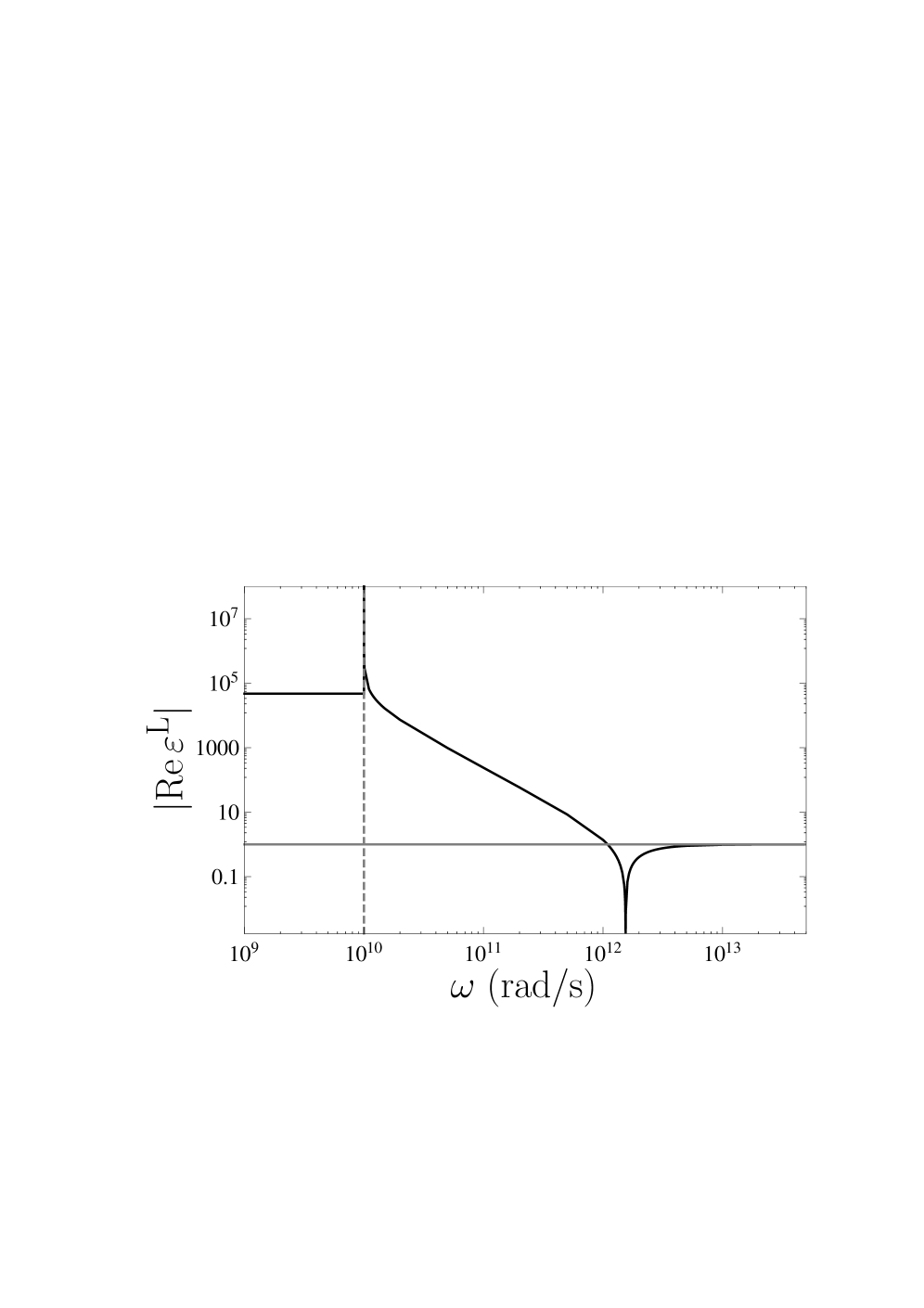
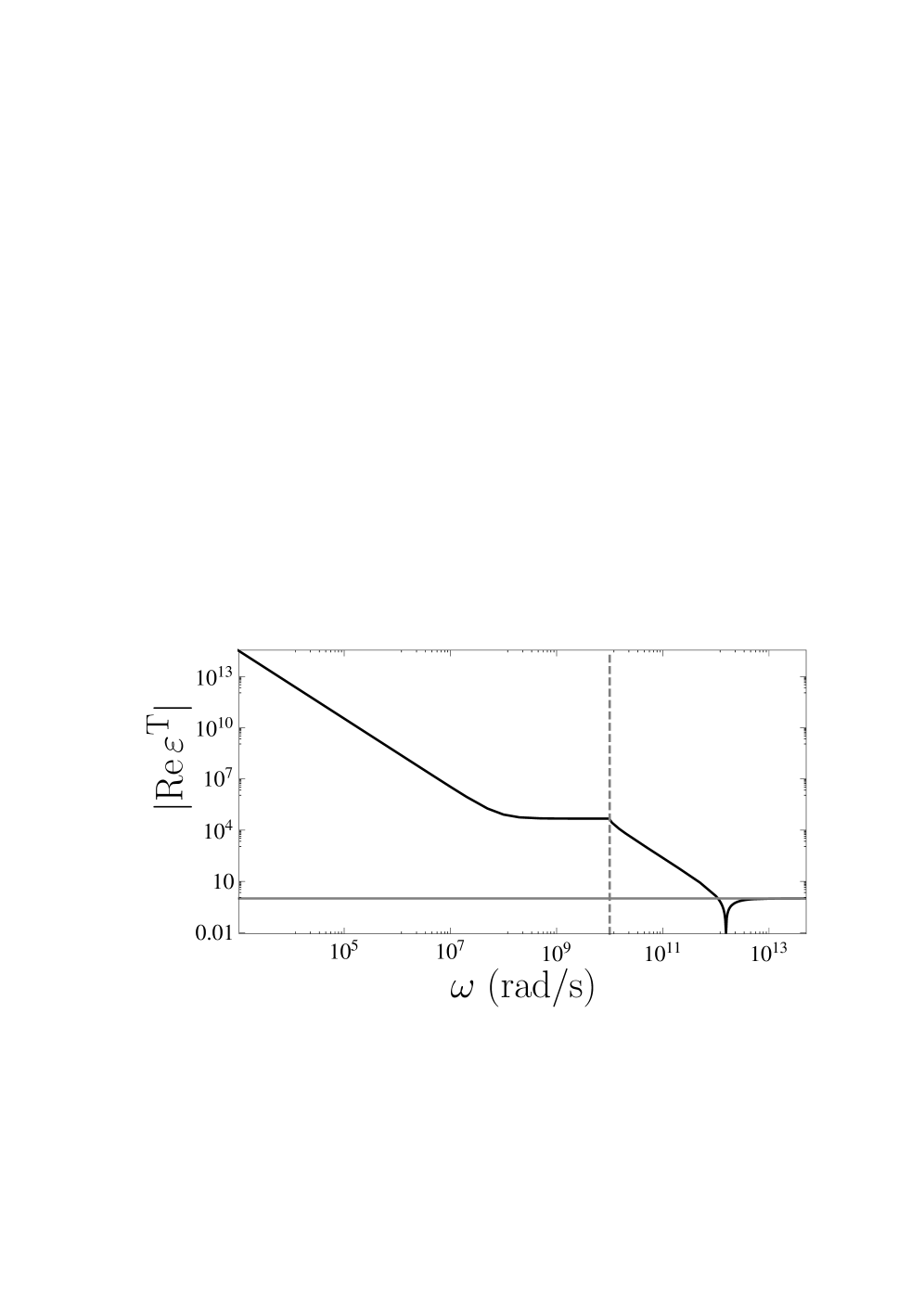
The calculated dielectric function of graphene demonstrates a complex relationship with frequency, characterized by both singularities and resonances. These features arise from the material’s unique electronic band structure and interband transitions. Singularities manifest as rapid changes in the dielectric function at specific frequencies, while resonances indicate enhanced absorption and scattering of electromagnetic radiation. The positions and strengths of these features are directly linked to the energy separations between the π and $\pi^*$ bands, and their frequency dependence reflects the momentum-dependent nature of these transitions. Accurate determination of these features is critical for predicting graphene’s optical and electronic behavior across a broad frequency spectrum.

The transverse dielectric function of graphene exhibits a ‘double pole’ singularity at a frequency of 0 $\omega = 0$ . This characteristic arises from the specific band structure of graphene and the resulting electronic transitions. The presence of this double pole significantly influences the material’s optical properties, particularly its response to electromagnetic radiation at low frequencies, leading to enhanced effects like strong plasmon excitation and increased absorption. This behavior is distinct from the single-pole response typically observed in conventional 2D materials and necessitates careful consideration when modeling graphene’s optical behavior.

Kramers-Kronig relations were implemented as a crucial validation step in the dielectric function calculation. These relations, derived from the principle of causality – that a response cannot precede a stimulus – mathematically connect the real and imaginary parts of any linear response function, including the dielectric function $\epsilon(\omega)$ . Specifically, the real part of the dielectric function at a given frequency is directly related to the Hilbert transform of the imaginary part at all other frequencies, and vice-versa. By applying these relations, we confirmed the consistency of our calculated dielectric function, ensuring that the predicted optical response adheres to fundamental physical principles and eliminating any unphysical behavior arising from numerical artifacts or model limitations. Deviations from the Kramers-Kronig relations would indicate errors in the calculation or an incomplete model.

The electronic structure of graphene, particularly at lower energies, is accurately described by the Dirac model, which treats electrons as massless Dirac fermions. This model simplifies the complex band structure by linearizing the energy dispersion relation near the Dirac points, resulting in a $\hbar \omega = v_F p$ relationship where $v_F$ is the Fermi velocity and $p$ is the momentum. This approximation is valid due to graphene’s unique band structure, where the valence and conduction bands meet at these points. The resulting Dirac Hamiltonian is then used within the random-phase approximation to calculate the dielectric function, providing a computationally efficient and accurate representation of graphene’s optical properties in the low-energy regime.

The logarithmic plot of graphene's transverse dielectric function's real component versus frequency at 300K and <span class="katex-eq" data-katex-display="false">q=100~\mbox{cm}^{-1}</span> reveals a threshold at <span class="katex-eq" data-katex-display="false">\omega=v_{F}q</span>. — The logarithmic plot of graphene’s transverse dielectric function’s real component versus frequency at 300K and $q=100~\mbox{cm}^{-1}$ reveals a threshold at $\omega=v_{F}q$ .

The Echo of Prediction: Implications and Future Failures

The Casimir effect, a measurable force arising from quantum fluctuations in the electromagnetic field, is profoundly sensitive to the material properties of intervening surfaces. Precisely calculating this force between graphene layers necessitates an accurate understanding of graphene’s dielectric function – a material property describing how it responds to electric fields. Prior discrepancies between theoretical predictions and experimental measurements, known as the ‘Casimir Puzzle’, stemmed largely from inaccuracies in modeling this function. Recent advances in determining graphene’s dielectric function, accounting for its unique two-dimensional electron system, have yielded significantly improved calculations of the Casimir force. This refined understanding not only resolves the longstanding puzzle, bringing theory and experiment into close agreement, but also provides a crucial foundation for exploring related phenomena and designing novel nanodevices leveraging this quantum force.

For years, the Casimir effect – a measurable force arising from quantum fluctuations in the vacuum – presented a puzzle when comparing theoretical calculations to experimental results, particularly involving materials like graphene. Discrepancies arose because accurately modeling graphene’s dielectric function – its ability to store electrical energy in an electric field – proved exceptionally difficult. Recent work, however, has yielded a refined understanding of this dielectric function, allowing for more precise calculations of the Casimir force. This improved modeling has demonstrably resolved the longstanding ‘Casimir Puzzle’, with predictions now aligning with experimental measurements. The convergence between theory and experiment not only validates the computational approach but also provides a robust foundation for exploring similar quantum effects in other novel materials and nanoscale systems, opening doors for advanced technological applications.

Accurately modeling the Casimir effect – the subtle force arising from quantum fluctuations in the vacuum – at realistic temperatures necessitates moving beyond the simplified conditions of zero temperature calculations. This requires the sophisticated framework of Thermal Quantum Field Theory, which accounts for the excitation of quantum fields at finite temperatures and the resulting thermal fluctuations. Applying this theory introduces complexities in calculating the Casimir force, as it involves summing over an infinite number of thermal modes and carefully considering the temperature-dependent dielectric function of materials like graphene. The resulting predictions, however, are crucial for understanding the behavior of nanodevices operating in real-world conditions, where thermal effects are unavoidable and can significantly alter the magnitude and range of the Casimir force, potentially influencing device stability and performance.

A precise understanding of a material’s dielectric function – how it responds to electric fields – is intrinsically linked to its conductive properties, specifically longitudinal and transverse conductivities. This relationship isn’t merely theoretical; it presents tangible opportunities for innovative device design. By carefully tailoring the dielectric function through material engineering or external stimuli, it becomes possible to manipulate how electromagnetic waves propagate and interact with the material, offering pathways to create novel metamaterials, advanced sensors, and highly efficient energy harvesting devices. For instance, controlling both longitudinal and transverse conductivities allows for precise control over plasmonic resonances, which are crucial for nanoscale optical circuits and enhanced light-matter interactions. This interplay opens the door to devices where electrical and optical properties are seamlessly integrated, potentially revolutionizing fields ranging from telecommunications to biomedical engineering.

The pursuit of definitive material properties, as illustrated by this exploration of graphene’s dielectric function, inevitably encounters limitations. The study meticulously charts the unusual behaviors – the double pole at zero frequency – yet these aren’t necessarily ‘problems’ to be solved, but inherent characteristics of complex systems. As Paul Feyerabend observed, “Anything goes.” This echoes the finding that seemingly anomalous behavior might resolve existing puzzles like the Casimir effect; a willingness to embrace the unexpected, rather than forcing conformity to pre-conceived theoretical frameworks, is paramount. The perfect theoretical architecture, neatly predicting all behaviors, remains a comforting myth; graphene, in its complexity, simply resists such totalizing ambition.

What Lies Beyond?

The exploration of graphene’s dielectric function, as presented, does not so much resolve puzzles as relocate them. The double pole at zero frequency – a peculiarity predicted, not explained – suggests a deeper resonance within the material’s response to fields. It is a confession, this theoretical result, admitting that the simple models have already failed to fully account for the observed behavior. The Casimir effect, seemingly addressed, now appears as a particularly loud symptom of a systemic misunderstanding.

Future inquiry will inevitably drift toward the limitations of the approximations employed. The very act of calculating a dielectric function presupposes a homogeneity, a separation of scales, that may be fundamentally untrue for a material existing at the edge of dimensional reduction. The evanescent waves, so crucial to the theoretical framework, are ghosts haunting the boundaries of predictability. Their influence, though mathematically contained, hints at unmodeled interactions, a constant erosion of the idealization.

The Kramers-Kronig relations, the bedrock of this analysis, are not laws but agreements – temporary truces in the war against inconsistency. The silence of the system, should further investigation fail to uncover more complex phenomena, will not be proof of understanding, but merely evidence of a limited attention span. The true work, it seems, is not to find answers, but to cultivate the patience for endless questioning.

Original article: https://arxiv.org/pdf/2601.10478.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

The Fragility of Prediction: Graphene’s Quantum Signature

First Principles: The Illusion of Control

Revealing the Signature: Validating the Prediction

The Echo of Prediction: Implications and Future Failures

What Lies Beyond?

See also: