Harnessing the Quantum Nature of Light and Matter at the Nanoscale

Author: Denis Avetisyan

A new theoretical framework clarifies the fundamental interactions between light and matter in nanophotonic systems, revealing regimes of exceptionally strong coupling.

Polariton dispersion reveals a complex interplay between light and matter, where the coupling of excitons and photons-illustrated by the <span class="katex-eq" data-katex-display="false">\Omega_{k_\parallel}</span> relationship-creates hybrid light-matter quasiparticles whose electronic and photonic character-quantified by <span class="katex-eq" data-katex-display="false">\eta_{\mathbf{k}_\parallel}^{\mathrm{el}}</span> and <span class="katex-eq" data-katex-display="false">\eta_{\mathbf{k}_\parallel}^{\mathrm{ph}}</span>-is strongly dependent on momentum, ultimately influencing the population of plasmons in the ground state as described by the anomalous Hopfield coefficient <span class="katex-eq" data-katex-display="false">|x_{\mathbf{k}_\parallel}|^2</span> and its asymptotic behavior in the quasistatic limit <span class="katex-eq" data-katex-display="false">k_\parallel \gg \omega_p/c</span>. — Polariton dispersion reveals a complex interplay between light and matter, where the coupling of excitons and photons-illustrated by the $\Omega_{k_\parallel}$ relationship-creates hybrid light-matter quasiparticles whose electronic and photonic character-quantified by $\eta_{\mathbf{k}_\parallel}^{\mathrm{el}}$ and $\eta_{\mathbf{k}_\parallel}^{\mathrm{ph}}$ -is strongly dependent on momentum, ultimately influencing the population of plasmons in the ground state as described by the anomalous Hopfield coefficient $|x_{\mathbf{k}_\parallel}|^2$ and its asymptotic behavior in the quasistatic limit $k_\parallel \gg \omega_p/c$ .

This review details a microscopic quantum description of surface plasmon polaritons using the Power-Zienau-Woolley representation to explore ultrastrong coupling and refine our understanding of light-matter interactions.

Conventional descriptions of light-matter interactions at metal-dielectric interfaces often rely on approximations that obscure fundamental quantum behavior. This work, ‘Microscopic quantum description of surface plasmon polaritons: revealing intrinsic ultrastrong light-matter coupling’, develops a rigorous quantum theory of surface plasmon polaritons using the Power-Zienau-Woolley representation, demonstrating that these systems inherently operate in an ultrastrong coupling regime. This framework not only recovers established results for localized and propagating plasmonic excitations, but also predicts unconventional ground-state quantum fluctuations controllable via refractive index. Could this deeper understanding of quantum plasmonics pave the way for novel nanophotonic devices and quantum technologies?

The Limits of Classical Pictures

The Drude model, a cornerstone of classical electromagnetism, successfully describes the macroscopic behavior of conductors but falters when applied to nanoscale light-matter interactions. This limitation arises from its treatment of electrons as a free gas subject to collisions, neglecting the quantum mechanical effects that dominate at reduced dimensions. Specifically, the model inadequately captures energy dissipation mechanisms, such as Landau damping, which stem from the interaction of energetic electrons with the underlying electron sea. At the nanoscale, these quantum effects become significant, leading to deviations from Drude’s predictions and necessitating a more sophisticated framework to accurately model plasmonic phenomena and other light-matter couplings. The classical picture simply lacks the necessary nuance to account for the collective, quantum-driven behavior observed in these systems, hindering the design and optimization of nanoscale optical devices.

The behavior of electrons in materials isn’t simply the sum of individual particle actions; instead, collective phenomena emerge from the intricate interplay between countless electrons. Accurately representing these interactions necessitates abandoning the simplifications of semi-classical models, which treat electrons as individual particles subject to averaged potentials. A robust quantum framework is essential because it inherently accounts for electron correlation – the ways in which electrons influence each other’s behavior – and wave-like properties. These quantum effects become particularly pronounced at the nanoscale, where electron confinement and surface interactions dominate. $\Psi(r_1, r_2, ..., r_N)$ , the many-body wavefunction describing the system, encapsulates the correlations between all $N$ electrons, offering a far more realistic, though computationally challenging, picture of material behavior than classical approximations allow. This detailed understanding is pivotal for predicting and controlling the optical and electronic properties of materials, especially in areas like plasmonics and metamaterials where collective electron oscillations dictate material response.

The ability to accurately model plasmonic resonances is paramount, as these collective oscillations of electrons at the interface between metals and light directly influence a burgeoning field of technological applications. From highly sensitive biosensors capable of detecting single molecules to the development of metamaterials with unprecedented optical properties, the manipulation of these resonances is key. Precise modeling allows researchers to tailor the interaction of light with matter at the nanoscale, optimizing device performance and enabling functionalities unavailable with traditional materials. This requires moving beyond simple approximations and embracing the complexities of quantum electrodynamics to fully capture the behavior of light and electrons in these systems, ultimately unlocking the full potential of plasmonics for advanced technologies.

The plasmonic frequency sum rule, illustrated for a metallo-dielectric interface supporting a plasmonic mode at frequency <span class="katex-eq" data-katex-display="false">\omega_{\mu}</span>, demonstrates a complementary relationship with its inverted structure characterized by frequency <span class="katex-eq" data-katex-display="false">\tilde{\omega}_{\mu}</span>. — The plasmonic frequency sum rule, illustrated for a metallo-dielectric interface supporting a plasmonic mode at frequency $\omega_{\mu}$ , demonstrates a complementary relationship with its inverted structure characterized by frequency $\tilde{\omega}_{\mu}$ .

Beyond Perturbation: A More Complete Picture

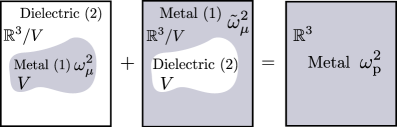
The Power-Zienau-Woolley (PZW) representation is a non-perturbative quantum mechanical formalism specifically designed for modeling electromagnetic interactions with materials at interfaces. Unlike approaches relying on perturbation theory, the PZW method directly solves Maxwell’s equations with appropriate boundary conditions, treating both the electromagnetic field and the material’s response on equal footing. This is achieved through the use of the Green tensor, which describes the electromagnetic field generated by a given current density, and the application of Helmholtz decomposition to separate the field into its static and dynamic components. Solutions to the Laplace equation are then employed to satisfy the required boundary conditions at the interface, enabling accurate calculation of induced currents and fields, even in strongly coupled regimes where perturbative methods fail.

The PZW representation utilizes the $\mathbf{G}$ Green tensor to describe the electromagnetic field generated by a given current density. This tensor satisfies the dyadic Green’s function equation and is crucial for calculating field enhancements near interfaces. The electromagnetic field is then decomposed using Helmholtz decomposition, separating it into a conservative (gradient) component and a solenoidal (curl) component, which simplifies analysis. Solutions to the Laplace equation, $\nabla^2 \phi = 0$ , are employed to determine the scalar and vector potentials, ultimately enabling accurate calculation of the fields and their interaction with electron densities at the interface, without requiring simplifying assumptions about the strength of the interaction.

The Power-Zienau-Woolley (PZW) representation facilitates the analysis of light-matter interactions beyond the limitations of perturbative approaches. Traditional methods often rely on weak coupling assumptions, restricting their accuracy when electromagnetic fields strongly interact with electron densities. The PZW formalism, however, provides a non-perturbative framework allowing for the investigation of strongly coupled regimes where these perturbative expansions fail. This capability is crucial for accurately modeling and controlling plasmonic phenomena, including surface-enhanced Raman scattering and localized surface plasmon resonance, as it accounts for the full interaction between light and collective electron oscillations without approximation. This allows for predictive modeling of systems exhibiting significant light-matter coupling and opens possibilities for designing novel plasmonic devices with enhanced functionality.

A spherical metallic nanoparticle of radius <span class="katex-eq" data-katex-display="false">a</span> with a frequency-dependent dielectric function <span class="katex-eq" data-katex-display="false">\varepsilon_{1}(\omega) = \varepsilon_{\in fty} - \omega^{2}_{p} / \omega^{2}</span> embedded in a dielectric medium <span class="katex-eq" data-katex-display="false">\varepsilon_{2}</span> exhibits closed-loop transverse <span class="katex-eq" data-katex-display="false">\mathbf{P}_{\perp}</span> and diverging longitudinal <span class="katex-eq" data-katex-display="false">\mathbf{P}_{\parallel}</span> polarization fields for its fundamental localized plasmon mode. — A spherical metallic nanoparticle of radius $a$ with a frequency-dependent dielectric function $\varepsilon_{1}(\omega) = \varepsilon_{\in fty} - \omega^{2}_{p} / \omega^{2}$ embedded in a dielectric medium $\varepsilon_{2}$ exhibits closed-loop transverse $\mathbf{P}_{\perp}$ and diverging longitudinal $\mathbf{P}_{\parallel}$ polarization fields for its fundamental localized plasmon mode.

Collective Excitations: The Birth of Polaritons

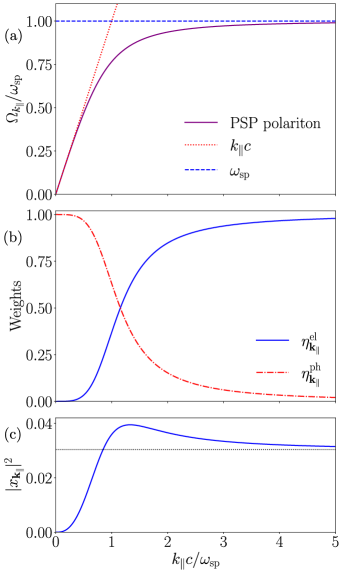
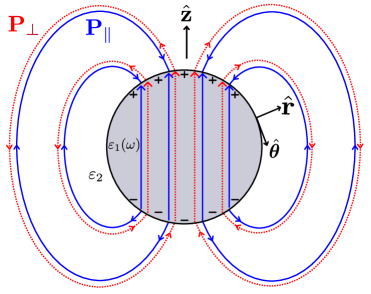
Surface plasmon polaritons (SPPs) are fundamentally hybrid electromagnetic modes that originate from the coherent interaction of photons with the free electron gas at the interface between a metal and a dielectric material. This strong coupling results in a collective oscillation of electrons, termed a plasmon, which is then coupled to the electromagnetic field of light, creating the SPP. The resulting excitation possesses characteristics of both light and electron oscillations, exhibiting an electric field that is bound to the interface and decays exponentially away from it. The frequency and wavevector of SPPs are determined by both the properties of the metal and dielectric, and their dispersion relation-the relationship between frequency and wavevector-differs significantly from that of free-space photons, enabling sub-diffraction light manipulation.

The Plane Wave Expansion (PZW) representation rigorously describes surface plasmon polaritons (SPPs) by decomposing the electromagnetic field into a superposition of plane waves. This approach allows for the consistent treatment of both localized surface plasmons (LSPs) – supported by nanoscale metallic structures – and propagating SPPs which exist at smooth metal-dielectric interfaces. By solving Maxwell’s equations with appropriate boundary conditions using the PZW method, one obtains the dispersion relation $\omega(k)$ which dictates the relationship between angular frequency ω and wavevector $k$ for SPPs. This dispersion relation, and the associated propagation length or decay constant, fully characterizes the SPP’s behavior and is fundamental for analyzing and predicting their response in plasmonic devices and structures.

The dispersion relation, which maps the frequency of SPPs to their wavevector, dictates how light propagates and is confined at the metal-dielectric interface; deviations from free-space light propagation are key to nanoscale control. Simultaneously, the decay length-the distance over which the SPP amplitude diminishes-directly impacts the propagation distance and thus the size and efficiency of plasmonic devices. Accurate characterization and control of both the dispersion relation and decay length, which are material and geometry-dependent, are therefore essential for optimizing device performance; for example, shorter decay lengths enable stronger field confinement but limit propagation distance, while manipulating the dispersion relation allows for subwavelength focusing and enhanced light-matter interactions. Device design often involves trade-offs between these parameters, necessitating precise fabrication and characterization techniques to achieve desired functionalities.

The ground-state population of bulk plasmons decreases with increasing mode order for both a metallic sphere and its complementary cavity <span class="katex-eq" data-katex-display="false">\epsilon_2 = 1</span> and <span class="katex-eq" data-katex-display="false">\epsilon_\in fty = 1</span>, converging to the flat interface limit. — The ground-state population of bulk plasmons decreases with increasing mode order for both a metallic sphere and its complementary cavity $\epsilon_2 = 1$ and $\epsilon_\in fty = 1$ , converging to the flat interface limit.

Beyond Coupling: A New Regime of Interaction

The transition to the ultrastrong coupling regime signifies a fundamental shift in how light and matter interact. Traditionally, light and matter are treated as separate entities, with light perturbing the material’s properties. However, when the strength of this interaction overwhelms the inherent energy scales within the material itself – specifically, exceeding the energy required to excite the material – this distinction blurs. The system no longer behaves as simply light interacting with matter, but rather as a fundamentally hybridized state. This isn’t merely a stronger version of typical light-matter interaction; it’s a qualitatively different phenomenon where the very definition of excitation becomes ambiguous, paving the way for entirely new physical properties and potential technological applications. $\hbar g > \hbar \omega_0$ , where $g$ is the coupling strength and $\omega_0$ the bare energy level, defines this critical threshold.

The interaction of light and matter, when sufficiently intense, gives rise to quasiparticles known as polaritons – fundamentally hybrid entities possessing characteristics of both photons and material excitations. These are not merely photons dressed by matter, but genuinely new states with dramatically altered spectral properties; energy levels are significantly reshaped, and the very definition of absorption and emission becomes blurred. Unlike traditional excitations, polaritons exhibit a mixed light-matter nature, allowing for strong interactions and collective behavior at relatively low densities. This hybridization leads to phenomena such as enhanced light-matter interaction, modified dispersion relations, and the potential for novel optoelectronic devices capitalizing on these unique characteristics. The study of polaritons represents a shift in how light and matter are considered, moving beyond separate entities to a unified description of coupled systems.

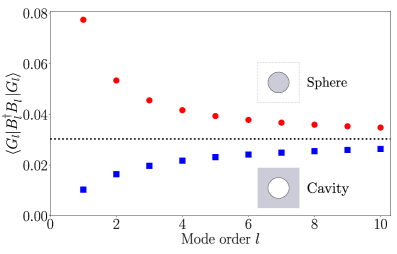
Rabi splitting, observed as the distinct separation of energy levels in spectroscopic measurements, serves as a key indicator of robust light-matter interaction and directly confirms the creation of polariton states – quasiparticles that are hybrid light-matter excitations. Recent modeling of plasmon-photon systems reveals these systems inherently operate within the ultrastrong coupling regime, a condition where the interaction strength becomes comparable to the energy of the system itself. Notably, the simulations demonstrate a finite population of plasmons remaining in the ground state – approximately 0.03 – even at zero excitation, a characteristic feature distinguishing ultrastrong coupling from its weaker counterpart, strong coupling, and highlighting the profound modification of the system’s fundamental properties.

A metal-dielectric interface is modeled with a metallic region (1) exhibiting a Drude dielectric function <span class="katex-eq" data-katex-display="false">\varepsilon_1(\omega) = \varepsilon_\in fty - \omega_p^2/\omega^2</span> and a dielectric region (2) with a positive dielectric constant <span class="katex-eq" data-katex-display="false">\varepsilon_2 > 0</span>, with the unit vector <span class="katex-eq" data-katex-display="false">\mathbf{N}</span> normal to the interface and pointing into the dielectric. — A metal-dielectric interface is modeled with a metallic region (1) exhibiting a Drude dielectric function $\varepsilon_1(\omega) = \varepsilon_\in fty - \omega_p^2/\omega^2$ and a dielectric region (2) with a positive dielectric constant $\varepsilon_2 > 0$ , with the unit vector $\mathbf{N}$ normal to the interface and pointing into the dielectric.

The Limits of Perfection: A Question of Loss

The functionality of plasmonic devices is intrinsically linked to the management of energy loss, primarily through two key mechanisms: Ohmic losses and radiative damping. Omic losses arise from the resistance encountered by the accelerated electrons within the metal, converting kinetic energy into heat and limiting the propagation length of surface plasmons. Radiative damping, conversely, stems from the emission of photons as the oscillating electrons radiate energy, effectively shortening the lifetime of the plasmonic excitation. Both phenomena contribute to a reduction in signal strength and overall device efficiency; a model demonstrates a bulk plasmon population of $3.0 \times 10^{-2}$ , and a frequency shift of $\omega_p$ . Consequently, a thorough understanding and mitigation of these dissipative processes are paramount for realizing high-performance plasmonic technologies, influencing design choices and material selection to maximize energy confinement and signal amplification.

A thorough comprehension of energy dissipation – stemming from both Ohmic losses and radiative damping – is paramount to the effective design of plasmonic systems. These losses fundamentally limit the efficiency with which devices can manipulate light and transfer energy, impacting performance metrics such as signal strength and operational speed. Precisely quantifying the origin and magnitude of these losses allows researchers to tailor material properties, refine device geometries, and ultimately maximize energy confinement and propagation lengths. The model demonstrates a bulk plasmon population of $3.0 \times 10^{-2}$ , and a frequency shift of $\omega_p$ . Such optimization is not merely theoretical; it directly translates to improved functionality in diverse applications, including highly sensitive biosensors, efficient solar energy harvesting, and the development of novel quantum technologies reliant on coherent plasmon manipulation.

Current research endeavors are heavily invested in mitigating energy dissipation within plasmonic systems to substantially prolong the lifespan of plasmonic excitations. Recent modeling indicates a significant bulk plasmon population – registering at $3.0 \times 10^{-2}$ – alongside a measurable frequency shift denoted as $\omega_p$ , highlighting key parameters for optimization. Successfully minimizing these losses isn’t merely an academic pursuit; it directly unlocks the potential for breakthroughs in diverse fields. Enhanced plasmonic performance promises more sensitive and accurate sensors, dramatically improved efficiency in energy harvesting technologies, and the realization of novel quantum technologies reliant on coherent and long-lived quantum states. These advancements hinge on innovative material design and structural engineering aimed at reducing both Ohmic and radiative damping effects, ultimately paving the way for a new generation of plasmon-based devices.

The pursuit of increasingly refined models for light-matter interaction, as demonstrated in this microscopic quantum description of surface plasmon polaritons, feels… familiar. They’ll call it nanophotonics and raise funding, of course. But the core principle remains unchanged: elegant theories invariably collide with the messy reality of production. James Maxwell himself observed, “Science is a series of approximations, each one building upon the errors of the last.” This paper, with its Power-Zienau-Woolley representation and focus on ultrastrong coupling, is merely the latest, more complex approximation. It’s a beautiful, mathematically rigorous approximation, undoubtedly, but one destined to become tomorrow’s tech debt when someone inevitably tries to simulate it at scale. The documentation, naturally, will lie about the computational cost.

Where Do We Go From Here?

This rigorous application of the Power-Zienau-Woolley representation to surface plasmon polaritons delivers a mathematically satisfying description of ultrastrong coupling. The inevitable question becomes: what problems will arise when someone tries to build this? The theoretical elegance neatly sidesteps the manufacturing tolerances, material imperfections, and sheer messiness of real-world nanophotonics. Expect a flurry of papers attempting to reconcile these idealizations with fabrication realities – papers that will, predictably, introduce new parameters to explain why the theory doesn’t quite match the experiment. If code looks perfect, no one has deployed it yet.

The exploration of the quasistatic regime, while valuable, highlights a limitation. Most applications don’t operate in the quasistatic regime. The next step will be extending this framework to incorporate full retardation effects and dynamical behavior, which will undoubtedly complicate the already substantial mathematical machinery. This pursuit of increasing accuracy often yields diminishing returns, trading theoretical completeness for practical tractability. It’s a familiar pattern.

Ultimately, this work provides a foundation-another layer in the stack. A beautiful foundation, perhaps, but still just a layer. The true test will be whether it enables genuinely novel devices or merely becomes another expensive way to complicate everything. The field will advance, of course. It always does. The more interesting question is whether that advancement will translate into something demonstrably useful, or simply a more refined understanding of why things don’t work as predicted.

Original article: https://arxiv.org/pdf/2601.11297.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/