Author: Denis Avetisyan
A new framework leverages quantum information inequalities to constrain the behavior of complex materials far from equilibrium.
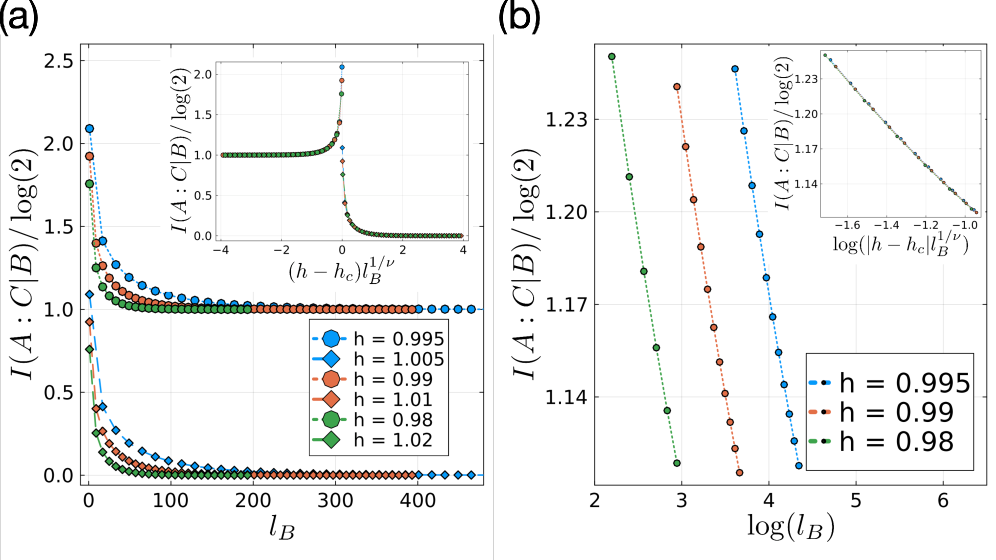
![The study demonstrates that conditional mutual information <span class="katex-eq" data-katex-display="false">I(l|l_B,p)</span> collapses onto a universal scaling function <span class="katex-eq" data-katex-display="false">f[(p-p_c)l_B^{1/\nu}]</span> with critical exponent <span class="katex-eq" data-katex-display="false">\nu=1</span> and critical point <span class="katex-eq" data-katex-display="false">p_c=1</span>, indicating a robust phase transition governed by the system’s parameters and reflected in the corresponding renormalization group flow.](https://arxiv.org/html/2602.04961v1/x2.png)
This review demonstrates how conditional mutual information can be used to map the renormalization group flow and assess the stability of nonequilibrium phases of matter.
Establishing robust criteria for stability in systems far from equilibrium remains a central challenge in condensed matter physics. In the article ‘Constraints on stability and renormalization group flows in nonequilibrium matter’, we demonstrate that quantum information inequalities, specifically bounds on conditional mutual information, provide novel constraints on renormalization group flows and phase stability. This approach reveals a non-perturbative link between information-theoretic quantities and the emergence of distinct phases, predicting, for instance, that fixed points with lower correlations are inherently more stable. Could these information-theoretic tools offer a unifying framework for understanding stability across diverse nonequilibrium systems, from classical symmetry-broken states to purely quantum phenomena?
Beyond Equilibrium: Unveiling Hidden Order
Conventional descriptions of matter often center on phases defined at equilibrium – stable, well-defined states characterized by minimal free energy. However, this approach overlooks the prevalence of mixed states in realistic systems. Unlike pure quantum states, which exist in a single, definite configuration, mixed states represent a probabilistic blend of multiple quantum possibilities. This is particularly crucial in systems interacting with their environment or driven far from thermal equilibrium, where energy exchange and constant interaction prevent the attainment of true equilibrium. Consequently, a complete understanding of material behavior necessitates acknowledging these mixed states, as they govern the properties of a vast range of physical phenomena-from the dynamics of open quantum systems to the behavior of materials under non-equilibrium conditions-that are inaccessible through traditional equilibrium-based analyses.
Characterizing complex phases of matter demands a shift beyond considering only simple, pairwise interactions between constituents; true understanding requires mapping the intricate web of correlations that emerge within these systems. Traditional methods often fall short because they presume interactions are limited to pairs, failing to capture the influence of multiple components acting in concert. To address this, researchers are increasingly turning to tools like Conditional Mutual Information (CMI), a measure that quantifies the information shared between two parts of a system, given knowledge of a third. CMI(A;B|C) effectively reveals how much knowing about component ‘A’ tells one about ‘B’, after accounting for what is already known from ‘C’. This allows for the detection of correlations that are not simply the sum of individual pairings, unveiling emergent properties and providing a more complete picture of the system’s underlying organization and behavior, particularly in strongly correlated materials and non-equilibrium states.
Conventional approaches to characterizing phases of matter often falter when confronted with systems deviating from strict equilibrium, revealing limitations in their ability to capture the full complexity of these states. Traditional methods, built upon assumptions of thermalization and well-defined order parameters, struggle to account for the intricate correlations and long-range entanglement present in non-equilibrium systems. Consequently, a paradigm shift is occurring, with researchers increasingly turning to information theory as a robust alternative. This framework, leveraging concepts like entropy, mutual information, and particularly Conditional\,Mutual\,Information\,(CMI), provides the necessary tools to quantify correlations beyond simple pairwise interactions and to characterize the emergent properties of these complex, often disordered, phases. By focusing on the information content of the system, rather than solely on energetic considerations, this new approach offers a more complete and accurate description of matter existing far from equilibrium, opening avenues for understanding phenomena in areas like quantum materials and driven quantum systems.
The behavior of many physical systems deviates significantly from the idealized conditions of thermal equilibrium, demanding a shift in theoretical approaches. Systems constantly interacting with their environment – known as open quantum systems – or those driven far from equilibrium by external forces, routinely exist in non-equilibrium states. These states are not adequately described by traditional methods focused on equilibrium properties; instead, understanding their dynamics requires considering the system’s full probability distribution and its evolution over time. This is particularly relevant in fields like quantum information processing, where maintaining coherence in a quantum system necessitates grappling with its unavoidable interaction with the surrounding environment, and in the study of biological systems, which are inherently non-equilibrium and driven by energy flows. Recognizing the prevalence and importance of these states is therefore crucial for advancing a more complete and realistic picture of the physical world.
Decoding Phase Transitions: A New Lens
The Renormalization Group (RG) flow is a technique used to investigate the phases and phase diagrams of systems exhibiting strong interactions. Unlike traditional approaches that rely on perturbation theory or mean-field approximations, the RG flow employs information-theoretic constraints – specifically, principles derived from information theory – to systematically analyze the system’s behavior across different length scales. This involves iteratively integrating out degrees of freedom, effectively ‘coarse-graining’ the system and revealing its essential characteristics. By imposing constraints based on quantities like the conditional mutual information I(X;Y|Z), the RG flow can determine fixed points corresponding to different phases and map out the phase boundaries separating them, even in scenarios where analytical solutions are unavailable. This methodology is particularly valuable for studying systems with many interacting components where conventional techniques fail due to the complexity of correlations.
The Renormalization Group (RG) flow, when constrained by the Conditional Mutual Information (CMI), provides a rigorous method for establishing bounds on system observables and pinpointing critical points. CMI, a measure of information shared between system variables beyond what is known from other variables, functions as a key constraint during the RG transformation. By enforcing that CMI remains non-negative throughout the coarse-graining process, the RG flow restricts the possible behaviors of the system. This constraint allows for the derivation of upper and lower bounds on quantities like correlation lengths and critical exponents, and importantly, it provides a means to identify fixed points of the RG flow which correspond to critical points in the system’s phase diagram. The non-negativity of CMI therefore serves as a selection principle, filtering out unphysical or unstable solutions and converging on the relevant critical behavior.
Traditional methods for analyzing phase transitions, such as mean-field theory and perturbative expansions, often struggle with systems exhibiting strong correlations due to the infinite number of interacting degrees of freedom or the divergence of perturbation series. These approaches typically rely on assumptions of weak interactions or local order, which break down in strongly correlated systems like those near critical points or exhibiting non-Fermi liquid behavior. The Renormalization Group flow approach circumvents these limitations by focusing on universal behavior and employing information-theoretic constraints-specifically, the use of Conditional Mutual Information CMI-to derive bounds on system behavior without explicitly solving for all interactions. This allows for the analysis of systems where traditional methods fail to converge or provide accurate predictions, effectively enabling the characterization of complex correlated phases and critical phenomena.
The Renormalization Group (RG) flow operates by systematically reducing the complexity of a system through a process of coarse-graining. This involves integrating out degrees of freedom at short distances, or high energies, effectively blurring out microscopic details that are not essential to the large-scale, macroscopic behavior. By repeatedly applying this procedure, the RG flow generates a sequence of simplified models that capture the dominant interactions and symmetries. This simplification allows for the identification of universal features – properties that remain consistent regardless of the specific microscopic details. Irrelevant details, those that diminish in importance with increasing length scales, are effectively eliminated, leaving only the essential parameters governing the system’s critical behavior and phase transitions.
![Using an alternate geometry, the critical mutual information (CMI) exhibits data collapse according to the scaling ansatz <span class="katex-eq" data-katex-display="false">I=f[(p-p_{c})l^{1/
u}]</span> with <span class="katex-eq" data-katex-display="false">p_{c}=0.109</span> and <span class="katex-eq" data-katex-display="false">
u=1.5</span>, characterizing the transition to symmetry-broken superfluidity.](https://arxiv.org/html/2602.04961v1/x7.png)
Disorder’s Dance: Unveiling Symmetry Breaking
The Random Bond Ising Model is a statistical mechanics model used to investigate the Strongly-Weakly Spontaneously Symmetry Breaking (SWSSB) transition, a type of phase transition distinct from conventional continuous or discrete transitions. In this model, each bond between spins is assigned a random value, introducing disorder into the system. This disorder alters the nature of the symmetry breaking, leading to a transition where the order parameter appears discontinuously even though the underlying Hamiltonian possesses a continuous symmetry. The model’s simplicity allows for analytical and numerical investigations of SWSSB, providing a controlled environment to study the critical behavior and scaling properties associated with this unique type of phase transition, and serving as a benchmark for understanding more complex disordered systems.
The Nishimori line in the Random Bond Ising Model represents a specific parameter regime – defined by the external magnetic field h and the bond disorder J – where analytical calculations become significantly simplified. This line is characterized by the property that the probability distribution of the magnetization is symmetric around zero, even in the presence of a non-zero external field. Consequently, calculations of physical observables, such as the free energy and magnetization, can be performed using replica symmetry, avoiding the complexities associated with replica symmetry breaking which are typically required for disordered systems. The location of the Nishimori line is determined by the relationship between the external field and the distribution of the random bonds, and it serves as a crucial tool for understanding the critical behavior of the model near the phase transition.
Investigation of the Random Bond Ising Model in the vicinity of the Nishimori line allows for the precise determination of critical exponents that characterize the Strongly-Weakly Spontaneously Symmetry Breaking (SWSSB) transition. Calculations demonstrate that the correlation length exponent, ν, associated with the diverging spatial correlations near the critical point, is equal to 1.5. This value is obtained through analysis of scaling functions and finite-size scaling techniques applied to simulations and theoretical calculations performed near the Nishimori line, providing a key parameter in understanding the universality class of the SWSSB transition in this disordered system. Furthermore, analysis along the Nishimori line simplifies calculations and offers a tractable pathway to determine other critical exponents and scaling functions relevant to the phase transition.
The Strongly-Weakly Spontaneously Symmetry Breaking (SWSSB) transition in the Random Bond Ising Model arises from a competition between the random, non-uniform bonds and the ferromagnetic interactions between spins. This interplay dictates the model’s phase diagram, characterized by a disordered phase at high temperatures and a partially ordered phase at low temperatures. Quantitative analysis has pinpointed a critical point, denoted as p_c = 0.109 , which represents the threshold beyond which long-range order emerges despite the presence of disorder. This critical point defines the boundary between the disordered and partially ordered phases and is crucial for understanding the system’s collective behavior as it transitions between these states.
![The critical mutual information (CMI) for the transition from trivial to SWSSB in two dimensions scales with parameter <i>p</i> for varying values of <span class="katex-eq" data-katex-display="false">l_B</span>, exhibiting data collapse when analyzed using the scaling ansatz <span class="katex-eq" data-katex-display="false">I(A:C|B)=f[(p-p_c)l_B^{1/\nu}]</span> with <span class="katex-eq" data-katex-display="false">p_c = 0.109</span> and <span class="katex-eq" data-katex-display="false">\nu = 1.5</span>.](https://arxiv.org/html/2602.04961v1/x4.png)
Beyond the Model: Echoes in Reality
The analytical techniques and conceptual framework established within this study are not limited to the specifics of the Random Bond Ising Model; instead, they represent a broadly applicable toolkit for investigating a diverse array of disordered systems. These methods, centered around understanding the interplay between disorder and correlation, can be readily adapted to analyze systems exhibiting similar characteristics – including those found in spin glasses, disordered quantum systems, and even certain aspects of neural networks. The emphasis on identifying and characterizing critical behaviors, such as the critical disorder strength and associated anomalous dimensions, provides a powerful approach for unraveling the complex interplay of interactions and randomness in any system where disorder plays a significant role in shaping emergent phenomena. This extends the impact beyond condensed matter physics, offering potential insights into fields dealing with complex, disordered landscapes and their associated phase transitions.
The critical properties revealed by this research, particularly the calculated value of the critical mutual information (CMI) and the demonstrated limitations of conventional analytical techniques, resonate strongly with challenges in both quantum information theory and materials science. A precise understanding of CMI is crucial for quantifying entanglement and correlation in quantum systems, informing the development of robust quantum computing and communication protocols. Similarly, in materials science, the framework provides insights into the behavior of disordered materials near critical points, where subtle correlations dictate macroscopic properties. The demonstrated inadequacy of standard perturbative methods highlights the need for novel approaches to characterize these complex systems, potentially leading to the design of materials with tailored functionalities and enhanced performance. This work suggests that accurately capturing the interplay of disorder and correlation is paramount for advancing both fields, and opens avenues for applying these techniques to a broader range of correlated systems.
Continued investigation should extend these analytical techniques to systems exhibiting more intricate interactions and geometries, potentially revealing novel phases and transitions not captured by simpler models. A crucial avenue for future work lies in rigorously examining the role of ultraviolet (UV) finiteness – ensuring the theory remains well-defined at all energy scales – as violations could significantly alter predicted critical behavior. Specifically, exploring how finite-size effects and higher-order corrections impact the observed critical exponents and the calculated critical dimension will be essential for validating the robustness of these findings. Moreover, adapting these methods to study systems far from equilibrium could provide insights into dynamical phenomena and the emergence of complexity in correlated materials, offering a path towards understanding phenomena like glass formation and the behavior of quantum spin liquids.
This research establishes a novel framework for investigating phases that exist far from equilibrium, particularly within systems where interactions between components-known as correlated systems-give rise to complex, emergent behaviors. Through rigorous analysis, the study reveals that the Spin-Wave Symmetry-Breaking (SWSSB) phase exhibits an anomalous dimension of 2, indicating a unique scaling behavior not captured by traditional models. Critically, the framework pinpoints a Central Manifold Instability (CMI) value of \log 2 precisely at the transition between phases, providing a quantifiable marker for this critical point and offering insights into the system’s susceptibility to fluctuations and the emergence of order. This precise determination of the CMI value, coupled with the identified anomalous dimension, signifies a powerful new tool for characterizing these complex phases and understanding the fundamental principles governing their behavior.
The pursuit, as demonstrated in this exploration of nonequilibrium systems, isn’t merely about charting established paths but actively probing their limits. One concludes: ‘Nothing in life is to be feared, it is only to be understood.’ This sentiment echoes the methodology presented-deconstructing established renormalization group flows using quantum information inequalities. The paper doesn’t simply accept stability; it actively tests it, leveraging concepts like conditional mutual information to reveal underlying constraints. Every identified limit, every breach of expected behavior, is a philosophical confession of imperfection in our understanding of these complex systems-a testament to the power of reverse-engineering reality itself. The meticulous application of information theory reveals that the boundaries of stability aren’t absolute, but rather defined by the flow of information within the system.
Beyond Equilibrium: Charting the Unknown
The application of quantum information inequalities to the notoriously messy realm of nonequilibrium systems feels less like a solution and more like a calculated provocation. This work doesn’t solve the problem of understanding emergent behavior; it instead introduces a new set of constraints, demanding a stricter accounting of informational flows. The renormalization group, a tool built on the assumption of slowly varying parameters, now faces a sharper blade – the limits imposed by conditional mutual information. The question isn’t whether these constraints will always hold, but where, and why they break down. Those failures, after all, will likely reveal the most interesting physics.
The focus on Markov length as a key parameter suggests a natural path forward. But to truly reverse-engineer these systems, a deeper understanding of the relationship between information loss, symmetry breaking, and the emergence of phases is required. Convex decomposition, while powerful, feels like a first approximation. A more complete picture will demand tools that can handle the inherently nonlinear and potentially chaotic nature of information scrambling in strongly driven systems.
Ultimately, this isn’t about finding the ‘correct’ framework. It’s about systematically dismantling existing assumptions. The pursuit of equilibrium is a convenient fiction. The real universe doesn’t care about simplicity; it thrives in the gaps, the exceptions, the places where the rules are stretched to their breaking point. And it is in those broken pieces that the most surprising discoveries await.
Original article: https://arxiv.org/pdf/2602.04961.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Get the Bloodfeather Set in Enshrouded
- Gold Rate Forecast
- 10 Movies That Were Secretly Sequels
- Uncovering Hidden Order: AI Spots Phase Transitions in Complex Systems
- These Are the 10 Best Stephen King Movies of All Time
- One of the Best EA Games Ever Is Now Less Than $2 for a Limited Time
- Best Controller Settings for ARC Raiders
- Best Werewolf Movies (October 2025)
- USD JPY PREDICTION
- 4 TV Shows To Watch While You Wait for Wednesday Season 3
2026-02-06 20:54