Author: Denis Avetisyan
New research leverages Bayesian statistics to refine our understanding of the ultra-dense matter residing within neutron stars, revealing the limits of current observational constraints.
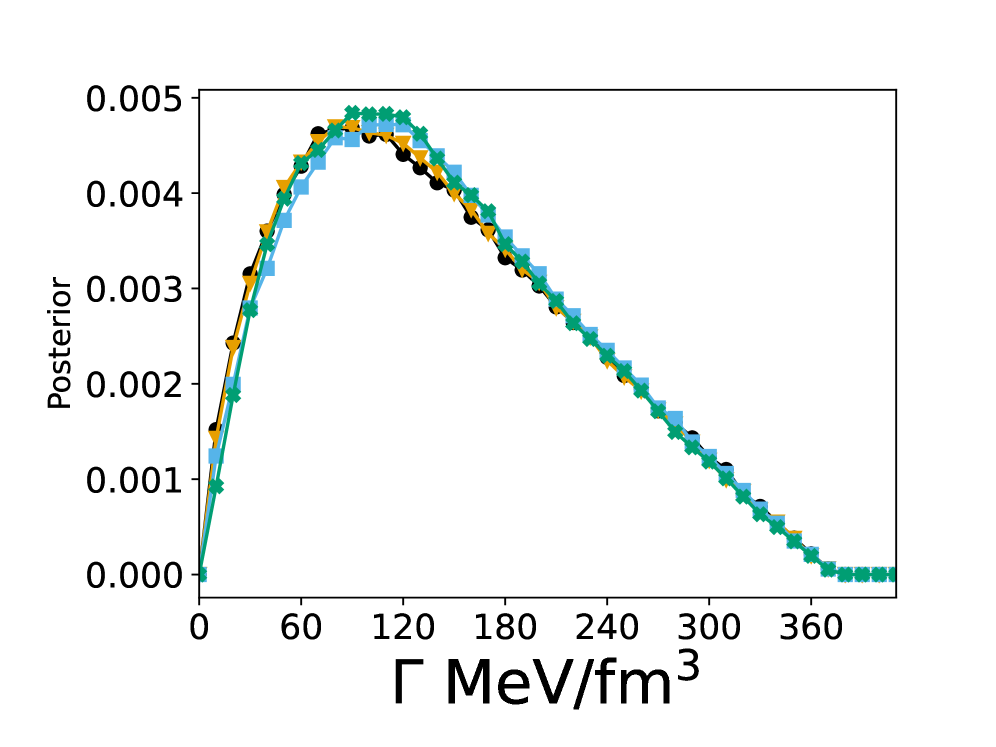
Bayesian inference constrains the equation of state of neutron star matter, highlighting the need for precise measurements to probe the hadron-quark crossover and the properties of quark matter.
The extreme densities within neutron stars present a fundamental challenge to our understanding of nuclear physics and quantum chromodynamics. This research, ‘Bayesian Constraints on the Neutron Star Equation of State with a Smooth Hadron-Quark Crossover’, employs Bayesian inference to constrain the equation of state governing matter at these densities, exploring a scenario with a smooth transition between hadronic and quark matter phases. Our analysis, utilizing gravitational-wave data, NICER observations, and theoretical consistency checks, reveals that current data primarily constrain the low-to-intermediate density behavior of neutron stars, yielding a most probable radius of R_{1.4}\sim eq 11.5-{13}.0 km. To what extent will next-generation precision radius measurements unlock the secrets of high-density matter and definitively reveal the presence – and properties – of quark matter within these stellar remnants?
The Density of Doubt: Probing Extreme Matter
Neutron stars represent the densest observable form of matter in the universe, offering an unparalleled natural laboratory for physicists. These stellar remnants pack the mass of one to two suns into a sphere roughly the size of a city – a density exceeding that of atomic nuclei. No terrestrial facility can replicate these conditions; even the most powerful particle colliders fall short of the extreme pressures found within a neutron star’s core. Consequently, observations of these objects – through electromagnetic radiation, gravitational waves, and potentially neutrinos – provide the only means to probe the behavior of matter at densities 10^{17} kg/m3 and beyond. This extreme environment tests the limits of nuclear physics, challenging existing models and potentially revealing new states of matter governed by exotic interactions.
The determination of a neutron star’s mass and radius, coupled with increasingly accurate measurements of its moment of inertia, presents a formidable challenge to current theoretical models of matter at ultra-high densities. Existing equations of state, which attempt to describe the relationship between pressure and density within these stellar remnants, frequently fail to simultaneously accommodate observed values for all three parameters. Discrepancies suggest that the extreme pressures within neutron stars may give rise to exotic forms of matter, such as hyperons, quarks, or even condensates, not fully accounted for in standard nuclear physics. Consequently, each new precise measurement serves as a crucial constraint, forcing refinement – or even complete revision – of the underlying physics that governs the behavior of matter under conditions unattainable in any terrestrial laboratory. The ongoing pursuit of these measurements promises to unlock profound insights into the fundamental nature of nuclear forces and the ultimate structure of matter itself.
The equation of state (EOS) describes the relationship between pressure, temperature, and density within matter, and at the crushing densities found in neutron stars – exceeding 10^{17} kg/m^3 – this relationship becomes extraordinarily complex. Determining the EOS is therefore paramount to understanding the fundamental forces governing nuclear interactions, as it dictates how neutrons and protons behave when squeezed beyond the limits achievable in terrestrial laboratories. Current theoretical models predict a wide range of possible EOS, influencing the star’s structure and stability, and ultimately impacting predictions for observable properties like radius and mass. Precise measurements from neutron star observations, particularly gravitational wave detections and X-ray burst analyses, provide critical constraints on these models, offering a unique window into the strong nuclear force and potentially revealing exotic states of matter beyond ordinary nuclei, such as hyperons or quark-gluon plasmas.
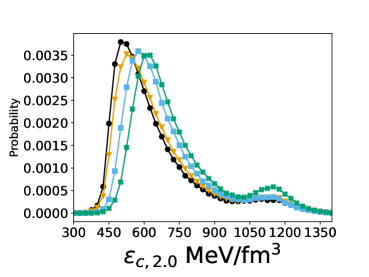
Constructing Reality: Building a Comprehensive Equation of State
The Hadronic Matter Equation of State (EOS) provides an accurate description of nuclear matter at baryon densities below the saturation density, approximately \rho_0 \approx 0.16 \text{ fm}^{-3} . This model relies on effective nuclear interactions and nucleon-nucleon scattering data to predict the pressure, energy density, and composition of matter consisting primarily of hadrons – protons, neutrons, and their excited states. A critical parameter informing this EOS is the Nuclear Symmetry Energy (NSE), which quantifies the energy cost associated with isospin asymmetry in nuclear systems. The NSE, typically expressed as E_{sym}(\rho) , is density-dependent and significantly influences the properties of neutron-rich matter, such as that found in neutron stars and core-collapse supernovae. Precise determination of the density dependence of E_{sym}(\rho) remains an active area of research, as it directly impacts predictions from the Hadronic Matter EOS.
At sufficiently high densities, typically exceeding those found in neutron star cores, nuclear matter is theorized to undergo a phase transition to quark matter. This transition involves the deconfinement of quarks and gluons, previously bound within hadrons. Describing this state requires a novel Equation of State (EOS) fundamentally different from the Hadronic Matter EOS. A key property governing quark matter is the Trace Anomaly, quantified as \Theta = \frac{m_q}{m_s} , where m_q represents the light quark mass and m_s the strange quark mass. The magnitude of the Trace Anomaly influences the pressure-density relationship and, consequently, the macroscopic properties of neutron stars, such as their mass-radius relationship and stability. Accurate modeling of the quark matter EOS, including the effects of the Trace Anomaly, remains a significant challenge in nuclear astrophysics.
A comprehensive Equation of State (EOS) Meta-Model necessitates a smooth transition between the Hadronic Matter EOS, valid at lower densities, and the Quark Matter EOS applicable at extreme densities. This is achieved through a parameterized crossover region, avoiding a sharp phase transition and maintaining thermodynamic consistency. Current observational constraints, derived from heavy-ion collision experiments and neutron star observations, indicate this crossover occurs within an energy density range of approximately 4-6ε₀, where ε₀ represents the saturation density of symmetric nuclear matter. The precise shape and parameters of this crossover are crucial for accurately modeling the behavior of matter under extreme conditions and are subject to ongoing research and refinement.
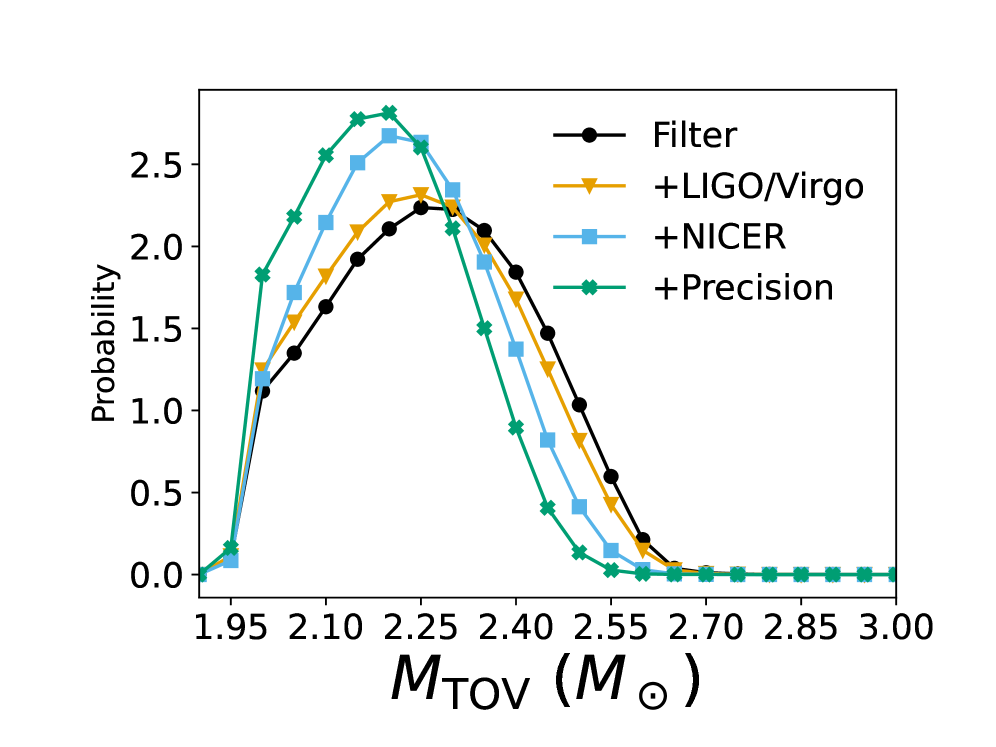
The Weight of Evidence: Bayesian Inference for Dense Matter Physics
Bayesian analysis offers a robust framework for determining the parameters defining the Equation of State (EOS) of dense matter. This statistical approach integrates pre-existing theoretical or experimental knowledge, expressed as a prior probability distribution, with observational data obtained from Neutron Star (NS) observations – including mass-radius relationships, gravitational wave signals, and tidal deformability. The method systematically updates the prior beliefs based on the evidence from NS observations, yielding a posterior probability distribution that represents the refined understanding of EOS parameters and their associated uncertainties. This contrasts with frequentist approaches by providing a full probability distribution over model parameters rather than single best-fit values, allowing for a more complete assessment of model reliability and predictive power.
The likelihood function, central to Bayesian inference, serves as a quantitative measure of how well a specific Equation of State (EOS) model aligns with available observational data from neutron stars. This function, denoted as L(\theta|D), where θ represents the EOS parameters and D the observed data (e.g., mass and radius measurements), assigns a probability to the parameters given the observations. A higher likelihood value indicates greater compatibility between the model and the data. During parameter estimation, the likelihood function is maximized – or, equivalently, its negative logarithm is minimized – to identify the parameter values that best explain the observed neutron star properties. This process effectively weighs different EOS models based on their ability to reproduce the empirical evidence, guiding the Bayesian analysis toward the most plausible parameter space.
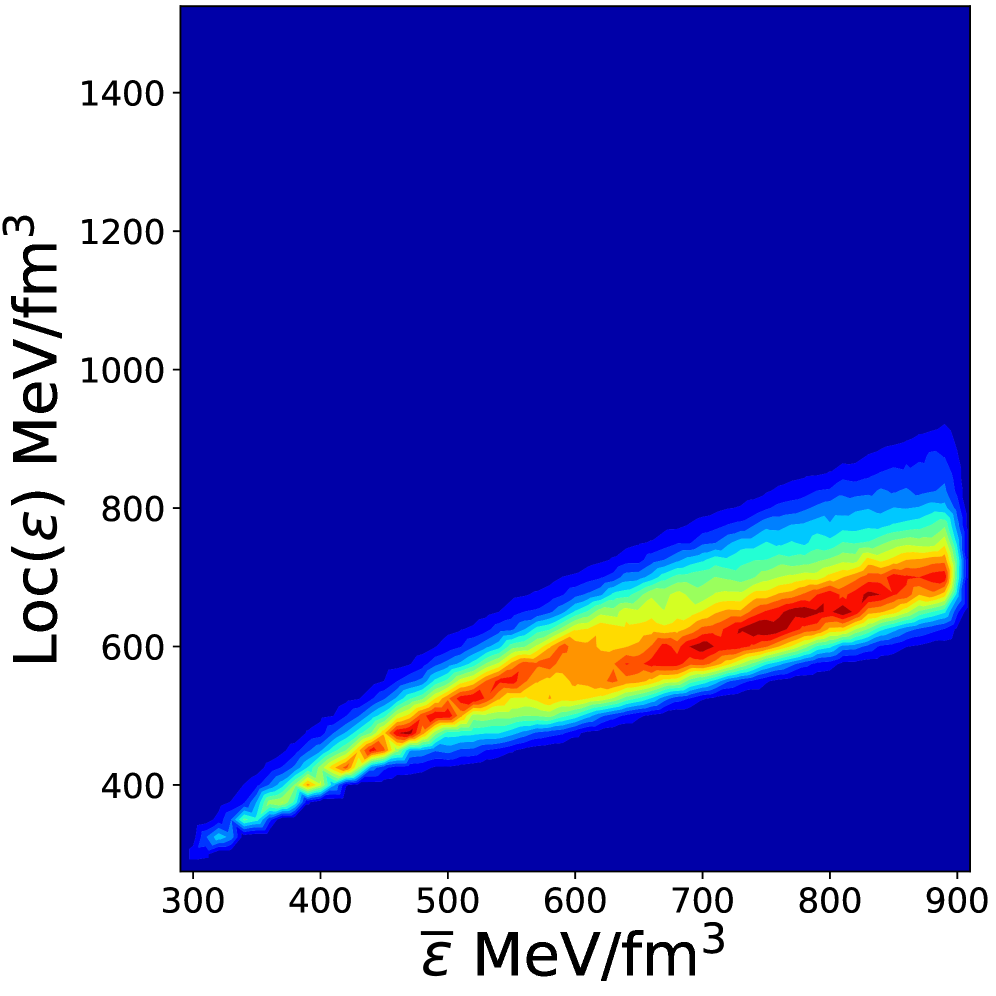
The posterior distribution, generated through Bayesian analysis of the Equation of State (EOS) parameters, represents the probability distribution of those parameters after incorporating both pre-existing knowledge – the prior – and new information derived from Neutron Star observations. This updated distribution allows for a quantifiable assessment of parameter uncertainty. Current analysis of this posterior distribution indicates the width of the crossover region – the area where the EOS transitions between different phases of dense matter – is constrained to approximately 0.5-1ε₀, where ε₀ represents a characteristic energy scale for the transition. This narrowing of the crossover region provides improved constraints on the underlying physics governing the behavior of matter at extreme densities.
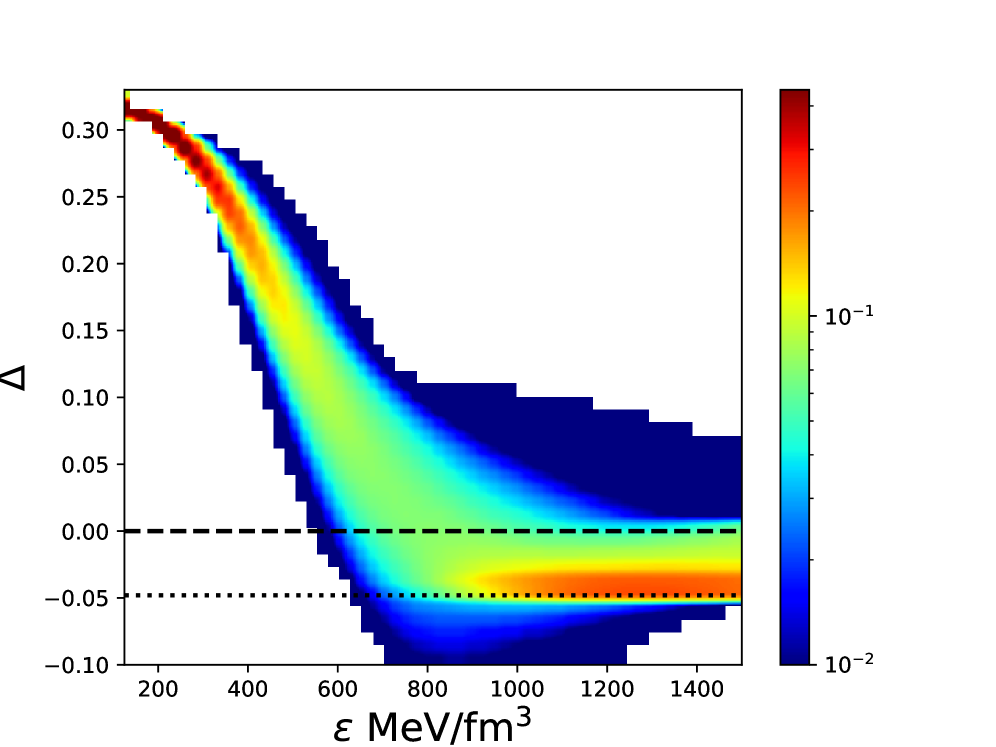
The Sound of Limits: Constraining the Crossover with Speed of Sound
The speed of sound within ultra-dense matter, such as that found in neutron stars, provides a crucial window into its fundamental properties. This velocity isn’t simply about audible tones; it directly reflects how resistant the material is to compression – its stiffness – and how readily it responds to pressure changes. A higher speed of sound indicates a stiffer equation of state (EOS) , meaning a greater pressure increase is needed for a given density change. Conversely, a slower speed suggests greater compressibility. Because the EOS dictates the relationship between pressure and density throughout a neutron star, precisely measuring or constraining the speed of sound at different densities allows scientists to map out the internal structure and composition of these extreme objects, distinguishing between different theoretical models and gaining insights into the behavior of matter under conditions unattainable on Earth.
The precise nature of the transition between hadronic matter and the hypothesized quark matter at extreme densities within neutron stars remains a significant challenge in nuclear physics. Recent research demonstrates that incorporating constraints on the speed of sound within dense matter provides a powerful means of refining the parameters governing this crossover. The speed of sound, directly linked to the equation of state (EOS), acts as a sensitive indicator of compressibility and stiffness; by limiting its maximum value – current models suggest approximately 0.5 – researchers can effectively narrow the range of acceptable EOS models and, consequently, better define the crossover parameters. This approach allows for a more focused exploration of the conditions under which the transition occurs, ultimately improving the accuracy of predictions regarding neutron star properties and the behavior of matter under the most extreme conditions in the universe.
A precise understanding of the equation of state (EOS) of dense matter relies heavily on statistical methods that incorporate observational constraints. Recent studies leverage Bayesian inference – a powerful technique for updating probabilities based on new evidence – to refine EOS models by considering the speed of sound within neutron stars. This approach doesn’t simply assume a likely EOS, but rather assesses the probability of different EOS models given the observed constraints, particularly the maximum permissible speed of sound. Current research indicates that accepted models generally converge on a maximum speed of sound around 0.5, serving as a critical parameter in narrowing the range of possible EOS scenarios. Consequently, this combined methodology yields a more robust and reliable determination of the EOS, directly influencing calculations of neutron star properties such as mass, radius, and tidal deformability, and offering deeper insights into the behavior of matter at extreme densities.
The pursuit of a definitive equation of state for neutron stars, as detailed in this research, echoes a fundamental challenge in all theoretical endeavors. Like attempting to map the ocean’s depths, each model – whether based on hadronic or quark matter assumptions – is inherently limited by the available data and the assumptions embedded within its framework. As Mary Wollstonecraft observed, “The mind should not be suffered to stagnate; it should be perpetually supplied with new objects to excite its activity.” This holds true for physics; continuous refinement through Bayesian inference, acknowledging the uncertainties inherent in probing extreme densities, is vital. Current observations, the study reveals, primarily constrain the low-to-intermediate density behavior, a reminder that even the most sophisticated instruments offer only a partial glimpse beyond the event horizon of the unknown.
What Lies Beyond the Horizon?
This investigation, employing Bayesian inference to map the equation of state for dense matter, reveals a familiar truth: constraints tighten where observations accumulate, and speculation reigns in the unexplored. The current limits primarily delineate the behavior of matter at lower-to-intermediate densities, a region already touched by terrestrial experiments and decades of astrophysical observation. Any extrapolation towards the truly exotic – the quark matter posited at the core – remains tentative, a construction built on theoretical scaffolding. The trace anomaly, a subtle signal of changing fundamental interactions, offers a potential probe, but its unambiguous detection demands a precision that currently eludes detection.
It is crucial to remember that any model simplification – whether concerning the hadron-quark crossover or the speed of sound within these dense environments – requires strict mathematical formalization. The elegance of a solution should not overshadow the rigor of its derivation. The pursuit of ever more accurate measurements is, of course, paramount. However, one must acknowledge the inherent limitations of any observational program. A black hole doesn’t merely consume data; it highlights the boundaries of knowledge.
Future progress will likely hinge not only on refinements in astrophysical observations-gravitational waves from neutron star mergers, for instance-but also on a deeper understanding of the underlying quantum chromodynamics. The connection between thermodynamics and gravitation, illuminated by Hawking radiation, serves as a constant reminder: any theoretical framework, no matter how compelling, is ultimately a transient structure, potentially vanishing beyond the event horizon of observational verification.
Original article: https://arxiv.org/pdf/2602.06696.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Avengers: Doomsday Trailer – Top 10 Most Anticipated Reveals
- Where Winds Meet has skills inspired by a forgotten 20-year-old movie, and it’s absolutely worth watching
- Gold Rate Forecast
- 5 Great Psychological Thrillers Nobody Talks About
2026-02-09 16:17