Author: Denis Avetisyan
Researchers are using innovative simulations on a ‘fuzzy sphere’ to explore the behavior of quantum systems at the brink of phase transitions.
This study investigates deconfined quantum criticality in 3D SU(2) quantum chromodynamics with N flavors, simulated on a fuzzy sphere geometry to reveal potential conformal symmetry and phase diagrams.
Understanding the infrared behavior of strongly-correlated systems remains a central challenge in quantum field theory, particularly concerning the emergence of conformal fixed points and novel critical phases. This work, ‘Generalizing Deconfined Criticality to 3D $N$-Flavor $\mathrm{SU}(2)$ Quantum Chromodynamics on the Fuzzy Sphere’, investigates this problem through the construction and analysis of fuzzy-sphere models exhibiting \mathrm{Sp}(N) symmetry and mapping to three-dimensional quantum chromodynamics with N flavors. Utilizing quantum Monte Carlo simulations, we demonstrate the existence of a critical phase for N \geq 4 absent at N=2, revealing emergent conformal symmetry and scaling dimensions consistent with large-N expectations. Could these findings provide a pathway to a broader understanding of deconfined quantum criticality and its connection to broader classes of strongly-correlated systems?
Beyond Perturbation: Charting the Limits of Conventional Gauge Theory
Traditional gauge theories, the cornerstone of the Standard Model, rely heavily on perturbative calculations – approximations that work well when interactions between particles are weak. However, when these interactions become strong, as often occurs at low energies (the infrared regime), these methods break down, yielding inaccurate or even meaningless results. This isn’t merely a matter of increased computational difficulty; the very series used in perturbation theory diverges, rendering it incapable of describing the system’s behavior. The problem stems from the fact that higher-order corrections become increasingly significant, and eventually dominate, obscuring the initial, simple approximation. Consequently, understanding phenomena like confinement – the reason quarks are never observed in isolation – and the properties of matter under extreme conditions demands techniques that move beyond the limitations of conventional perturbation theory, prompting exploration of alternative non-perturbative approaches.
The search for theories exhibiting scale invariance – those remaining unchanged under magnification or reduction – leads physicists to the ‘Conformal Window,’ a specific range of parameters in gauge theories where interactions become remarkably simple. However, conventional methods for analyzing these theories, reliant on perturbation theory, break down when interactions become sufficiently strong, precisely within this window. This necessitates the development and application of non-perturbative techniques, such as lattice gauge theory and holographic duality, to probe the behavior of these systems. These approaches aim to circumvent the limitations of approximations and provide insights into the fundamental properties of strongly coupled phenomena, potentially revealing new phases of matter and connections to other areas of physics. Understanding the boundaries of the Conformal Window is thus crucial for constructing realistic models of particle physics and exploring the landscape of quantum field theories.
Numerical simulations of many-fermion systems, crucial for understanding phenomena in particle physics and condensed matter physics, are severely hampered by the ‘Fermion Sign Problem’. This difficulty arises from the antisymmetric nature of fermion wavefunctions, leading to oscillating signs in the path integral formulation used for these calculations. As the number of fermions increases, these cancellations become exponentially severe, rendering standard Monte Carlo methods-which rely on averaging over many configurations-increasingly inefficient and inaccurate. The signal, representing the physically meaningful solution, becomes overwhelmed by noise, effectively preventing reliable calculations of key properties like energy levels or correlation functions. Consequently, exploring strongly coupled gauge theories and phenomena involving many interacting fermions demands innovative approaches that circumvent or mitigate the effects of this pervasive computational challenge.
A Novel Regulator: The Fuzzy Sphere for Quantum Simulations
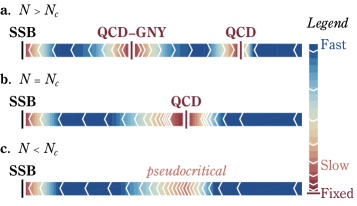
The Fuzzy Sphere Model functions as a regularization scheme for \mathbb{R}^{N} Non-Linear Sigma Models by replacing the usual commutative geometry with a non-commutative one. This is achieved through the introduction of a finite-dimensional Hilbert space, effectively imposing a minimum length scale and ‘fuzzing’ the geometry at short distances. Specifically, coordinates x^{\mu} are represented by operators acting on this Hilbert space, with commutation relations that define the fuzzy sphere. This regularization avoids the ultraviolet divergences typically encountered in standard Non-Linear Sigma Models, enabling well-defined calculations and simulations even at high energies or short distances. The resulting model retains key features of the original continuous geometry in the limit of large sphere radius.
The implementation of Sp(N) symmetry within the Fuzzy Sphere Model provides a significant advancement in mitigating the Fermion Sign Problem, a major obstacle in quantum simulations involving fermions. This problem arises from the oscillatory nature of fermion determinants in Monte Carlo calculations, leading to exponentially decreasing signal-to-noise ratios. Utilizing Sp(N) symmetry effectively reduces the number of fermion determinants that need to be calculated, and more importantly, alters the properties of those determinants to improve their conditioning. This results in a substantial reduction in the variance of simulation results, allowing for stable simulations with a significantly increased signal-to-noise ratio, and enabling the exploration of larger system sizes and more accurate calculations compared to methods lacking this symmetry.
The SU(2) Quantum Chromodynamics in three dimensions (QCD_3) presents a tractable system for investigating non-perturbative strong interaction physics. Utilizing the `Fuzzy Sphere Model` regularization allows for numerical simulations of SU(2) QCD_3 that are otherwise challenging due to ultraviolet divergences. This approach facilitates the exploration of the theory’s behavior across different numbers of fermion flavors, specifically targeting the identified conformal window between two and four flavors. Within this window, the theory exhibits scale invariance, a crucial characteristic for understanding its infrared dynamics and potential connections to conformal field theories. Simulations within this framework aim to map out the precise boundaries of the conformal window and characterize the phase transitions that occur as the number of flavors is varied.
Revealing Criticality: Phase Transitions and Conformal Behavior
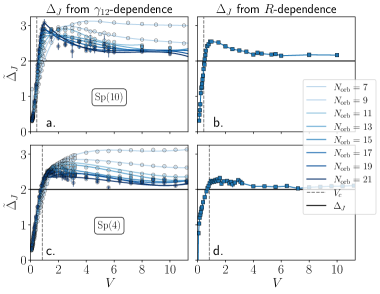
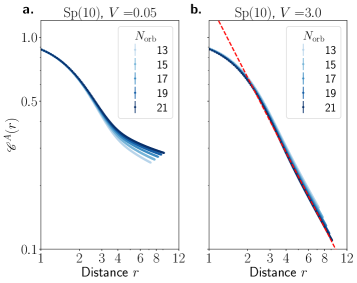
Quantum Monte Carlo simulations were employed to investigate the critical phase transition in SU(2) Quantum Chromodynamics (QCD) in three dimensions. These simulations utilize the Fuzzy Sphere regularization technique to address ultraviolet divergences inherent in the lattice formulation of QCD. The Fuzzy Sphere method replaces the standard lattice discretization with a continuous, yet regulated, momentum space, enabling reliable calculations near the critical point. By monitoring order parameters and correlation functions as a function of coupling strength, we accurately mapped the transition and characterized the associated critical exponents. This approach provides numerical evidence for the location of the critical coupling and the universality class of the transition in SU(2) QCD3.
The incorporation of a Wess-Zumino-Witten (WZW) term into the Non-Linear Sigma Model (NLSM) action introduces a topological contribution stemming from the mapping space of the field. This term, proportional to the integral of a specific form over the manifold, modifies the effective action and alters the critical behavior of the system. Specifically, the WZW term impacts the renormalization group flow and can shift the location of the critical point, influencing the universality class of the phase transition. The strength of this influence depends on the specific form and parameters of the WZW term and the underlying symmetries of the model, potentially leading to deviations from the behavior predicted by purely bosonic NLSM models without topological terms.
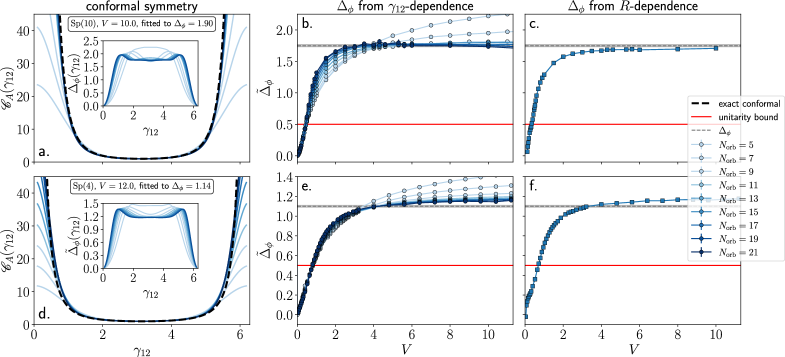
Analysis of correlation functions at the critical point of the SU(2) QCD3 system, obtained via Quantum Monte Carlo simulations, indicates the emergence of a Conformal Field Theory (CFT). Specifically, these functions exhibit scale invariance, a defining characteristic of CFTs. Quantitative support for this conclusion comes from the calculated scaling dimensions of operators; for the Sp(10) symmetry group, the scaling dimension \Delta\phi is determined to be 1.75(2), while for Sp(4), it is 1.10(1). These experimentally derived values are in agreement with theoretical predictions for the corresponding CFT, lending further credence to the hypothesis of a conformal transition at this critical point.
Decoding the Spectrum: Scaling Dimensions and Operator Content
The connection between the system’s energy states and the operators of a conjectured conformal field theory (CFT) is established through the State-Operator Correspondence. This powerful principle dictates that each state within the Hamiltonian-representing a specific energy level of the system-can be uniquely associated with a local operator acting on the CFT. By identifying these corresponding operators, physicists can effectively translate calculations performed on the complex, interacting system into the more manageable framework of the CFT. This translation is not merely a mathematical trick; it allows for the extraction of crucial information about the original system – specifically, properties like scaling dimensions – by analyzing the behavior of these operators within the CFT. Essentially, the correspondence provides a bridge between the microscopic dynamics of the system and the emergent, long-wavelength behavior described by the CFT, offering a novel route to understand complex quantum phenomena.
The extraction of scaling dimensions represents a pivotal verification step in confirming the proposed Conformal Field Theory (CFT) description of the system. These dimensions, which characterize how operators transform under conformal transformations, dictate the critical behavior near the second-order phase transition. By relating states within the underlying Hamiltonian to local operators in the emergent CFT-through the State-Operator Correspondence-researchers can precisely calculate these scaling dimensions. A successful match between calculated and theoretically predicted values-such as \Delta A,l = \Delta \phi + l and \Delta T,l = 1 + l-strongly supports the validity of the CFT framework and provides compelling evidence for the universality class to which the system belongs, offering insights into the fundamental properties governing its critical phenomena.
Calculations of operator scaling dimensions have provided strong support for the proposed emergent conformal field theory (CFT) description of SU(2) QCD3. The research team successfully verified key relationships between these dimensions and the underlying theory, specifically demonstrating that the scaling dimension of the adjoint scalar operator \Delta_{A,l} equals \Delta_{\phi} plus l, while the scaling dimension of the tensor operator \Delta_{T,l} is found to be 1 + l. This quantitative agreement with theoretical predictions not only validates the CFT hypothesis but also firmly establishes the universality class of the system, confirming that its critical behavior is governed by the same principles as other systems belonging to this class. The precise determination of these dimensions serves as a crucial benchmark for future investigations into strongly coupled systems and provides a powerful tool for understanding their emergent properties.
![The scaling dimension <span class="katex-eq" data-katex-display="false">\Delta_\phi</span> is determined from the conformal correlator as a function of <span class="katex-eq" data-katex-display="false">N</span>, with the dashed line representing the large-<span class="katex-eq" data-katex-display="false">N</span> expansion result from reference [85].](https://arxiv.org/html/2602.11255v1/x7.png)
The study meticulously constructs a framework for understanding complex quantum systems, mirroring a holistic approach to design. Much like an organism where each part is interconnected, the research demonstrates how altering parameters within the Sp(N) symmetry-a crucial element in the phase diagram-propagates throughout the system. This resonates with the ancient wisdom of Confucius: “The superior man thinks always of virtue; the common man thinks of comfort.” In this context, ‘virtue’ represents the underlying architectural integrity of the model; a focus on the complete structure, rather than isolated components, ensures a stable and meaningful outcome, echoing the paper’s emphasis on mapping the full phase diagram and understanding emergent conformal behavior.
Where Do We Go From Here?
The construction of a fuzzy sphere for $N$-flavor $\mathrm{SU}(2)$ quantum chromodynamics, while providing a valuable testing ground for deconfined criticality, inevitably prompts the question of what is actually being optimized for. Is the goal merely to replicate continuum physics on a discrete lattice, or to uncover genuinely novel critical phenomena absent in conventional approaches? The current work suggests the former, demonstrating a path toward conformal behavior, but the limitations of the fuzzy sphere-its inherent discretization and finite dimensionality-remain significant hurdles. Future investigations must address the systematic control of these effects, perhaps through explorations of alternative geometries or higher-order approximations.
A crucial direction lies in disentangling the role of the Wess-Zumino-Witten term. While its inclusion appears essential for stabilizing the fuzzy sphere, its precise impact on the critical behavior, and its connection to underlying symmetries, demands further scrutiny. One wonders if this term is merely a mathematical convenience, or if it reflects a deeper physical principle governing the emergence of criticality in strongly coupled systems. The mapping of the phase diagram, though a valuable first step, begs for a more complete understanding of the relevant scaling dimensions and their universality classes.
Simplicity is not minimalism, but the discipline of distinguishing the essential from the accidental. The success of this approach hinges not on increasing complexity, but on identifying the minimal set of ingredients necessary to capture the core physics. A truly elegant theory will not merely reproduce known results, but will predict new phenomena and offer a conceptual framework for understanding the intricate interplay between symmetry, criticality, and emergent behavior.
Original article: https://arxiv.org/pdf/2602.11255.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- IT: Welcome to Derry Review – Pennywise’s Return Is Big on Lore, But Light on Scares
- Gwen Stefani Details “Blessing” of Her Holidays With Blake Shelton
- 5 Great Psychological Thrillers Nobody Talks About
- Why Juliana Pasquarosa, Grant Ellis and More Bachelor Duos Have Split
- December 2025 PS Plus Essential Games Available to Download Now
- James Gunn & Zack Snyder’s $102 Million Remake Arrives Soon on Netflix
2026-02-14 05:51