Mapping the Logic of Equations

Author: Denis Avetisyan

---

A new approach uses geometric principles to reveal hidden structures within mathematical reasoning systems.

This review explores the construction of a latent space for equational theories using finite model theory and techniques inspired by machine learning.

Despite the foundational role of equational theories in mathematical logic, visualizing their relationships and inherent structure has remained a significant challenge. This paper, ‘The Latent Space of Equational Theories’, addresses this by constructing a latent space where each theory is positioned according to its statistical behavior on finite magmas, drawing on techniques from finite model theory and machine learning. We demonstrate that this approach reveals surprisingly well-defined chains of logical implication, offering a geometric perspective on reasoning itself. Could this latent space provide new insights into the complexity and categorisation of mathematical systems?

---

Foundations: The Essence of Equational Systems

Algebraic structures, from the familiar groups and rings to more esoteric constructions, all share a common foundation in the study of magmas – sets paired with a single binary operation. This seemingly simple concept serves as the most general algebraic framework; every algebraic structure is, at its core, a magma with additional axioms imposed. Considering a set S and a binary operation \circ, a magma (S, \circ) requires no further constraints, allowing for an expansive range of possibilities. Consequently, understanding magmas is crucial, as it provides the bedrock upon which more complex algebraic systems are built, influencing fields like abstract algebra, computer science, and even theoretical physics through applications in areas like automata theory and coding.

Equational theories offer a precise language for describing algebraic structures by focusing on the relationships between operations, expressed as equations. Rather than defining a structure through its elements and their actions, these theories specify the fundamental laws that govern those operations-for instance, the commutative law x <i> y = y </i> x or the associative law (x <i> y) </i> z = x <i> (y </i> z). This approach allows mathematicians to characterize an entire class of algebraic systems – like groups, rings, or lattices – simply by stating the equations that must hold true for its operations. Consequently, equational theories provide a powerful tool for establishing connections between different algebraic structures, revealing underlying similarities and differences, and ultimately building a comprehensive understanding of their relationships.

The comprehensive investigation into the relationships between equational theories required overcoming substantial computational hurdles. Establishing which theories logically imply others – a task seemingly simple in principle – quickly escalates in complexity with each additional theory considered. Researchers employed a systematic methodology to navigate this expansive landscape, meticulously analyzing 4694 distinct equational theories to chart their interdependencies. This exhaustive mapping wasn’t merely an exercise in enumeration; it demanded efficient algorithms and substantial computing resources to determine the precise implications between these algebraic structures, ultimately revealing a detailed network of connections within the field and providing a foundational resource for future research.

Ordering the Landscape: The Implication Preorder

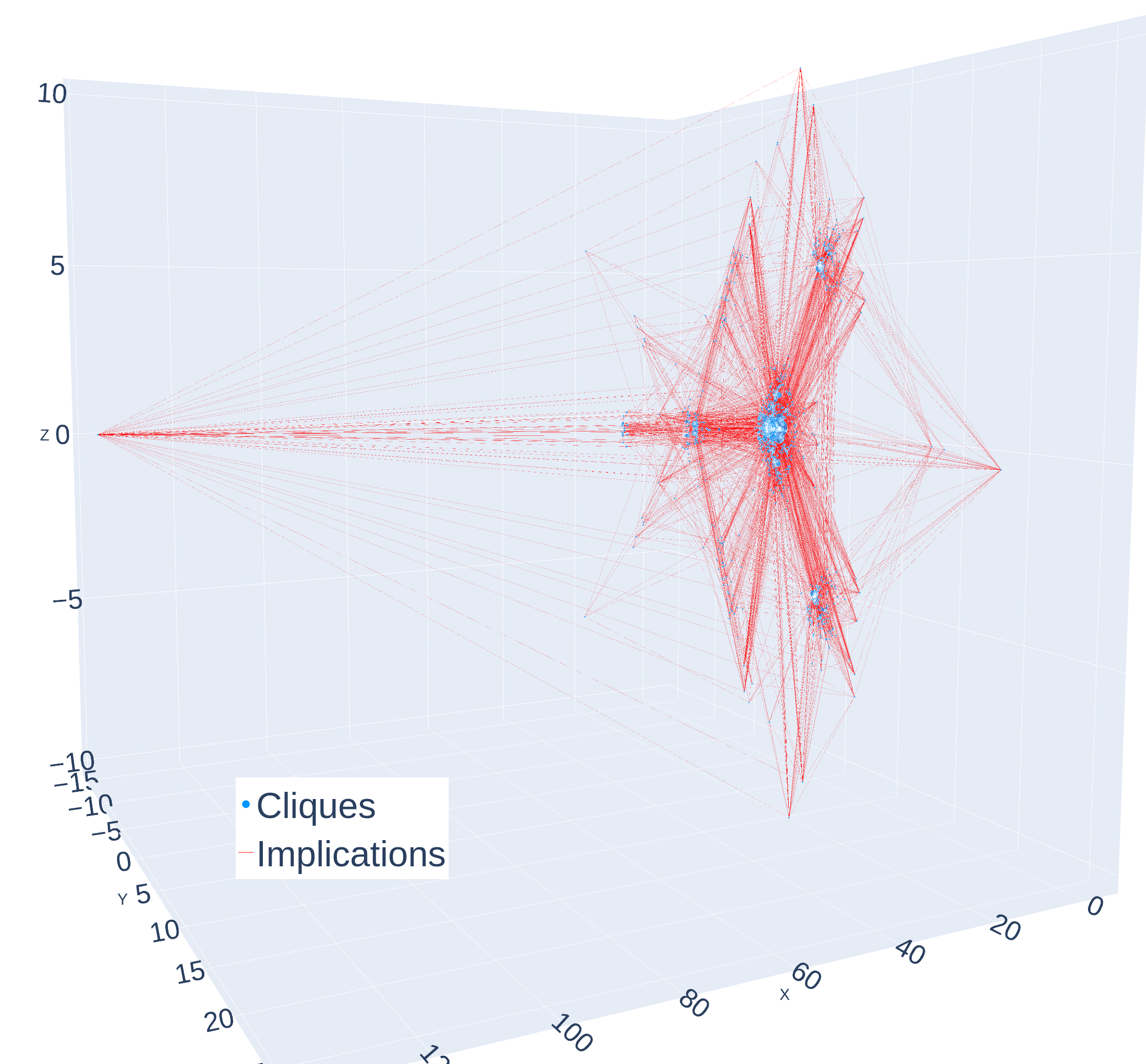
The Equational Theories Project culminated in the construction of the Implication Preorder, a comprehensive mapping of relationships between 4694 distinct equational theories. This involved a systematic analysis to determine which theories logically imply others, effectively establishing a partial order based on logical consequence. Each theory within the set was evaluated relative to all others, identifying instances where the axioms of one theory necessitate the truth of another. The resulting preorder provides a formal framework for comparing and contrasting these theories, revealing underlying connections and dependencies within the field of equational reasoning.

The Implication Preorder provides a structured framework for analyzing the relationships between equational theories, realized as a directed graph with 1415 vertices. Each vertex represents a distinct equational theory, and directed edges denote implication – a relationship where the consequences of one theory are contained within another. The “modulo reversibility” designation indicates that edges representing trivially reversible implications have been consolidated to reduce redundancy in the graph’s representation. This graph facilitates the systematic exploration of the space of equational theories, allowing researchers to identify hierarchies and dependencies between different algebraic systems and their defining equations.

The implication graph, constructed as part of the Equational Theories Project, comprises 4824 edges. Each edge represents a demonstrable implication between two equational theories following a simplification process; that is, one theory logically entails another after redundant equations have been removed. This edge count reflects the connections established between theories within the broader implication preorder, and is calculated modulo reversibility – meaning that if theory A implies theory B, the reverse implication (B implies A) is not necessarily represented as a separate edge to avoid redundancy in the graph’s representation of relationships.

Revealing Structure: Stone Pairings and Latent Spaces

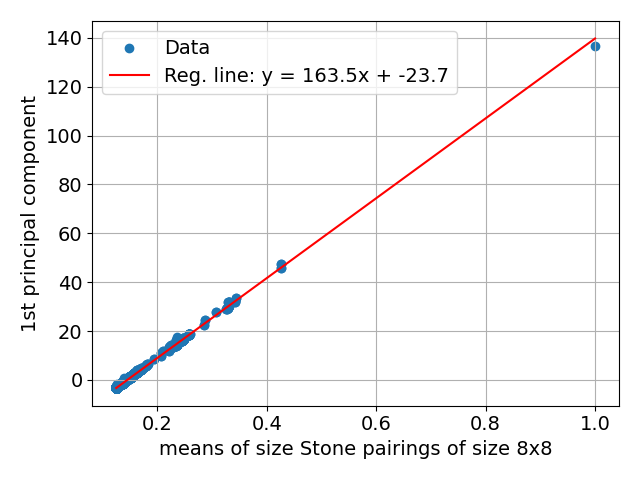
Stone pairings offer a method for assessing the truth of implications between equational theories by treating these theories as probability distributions over models. Specifically, a Stone pairing consists of a pair of probability measures, one defined on models of the first theory and the other on models of the second. An implication from the first theory to the second – stating that every model of the first also satisfies the second – is valid if and only if the support of the first measure is contained within the support of the second. This probabilistic approach allows for a quantifiable assessment of implication validity, moving beyond purely syntactic considerations and enabling the use of statistical methods to analyze relationships between equational theories. The pairing effectively maps models of one theory into the probability space of the other, allowing for a formal comparison.

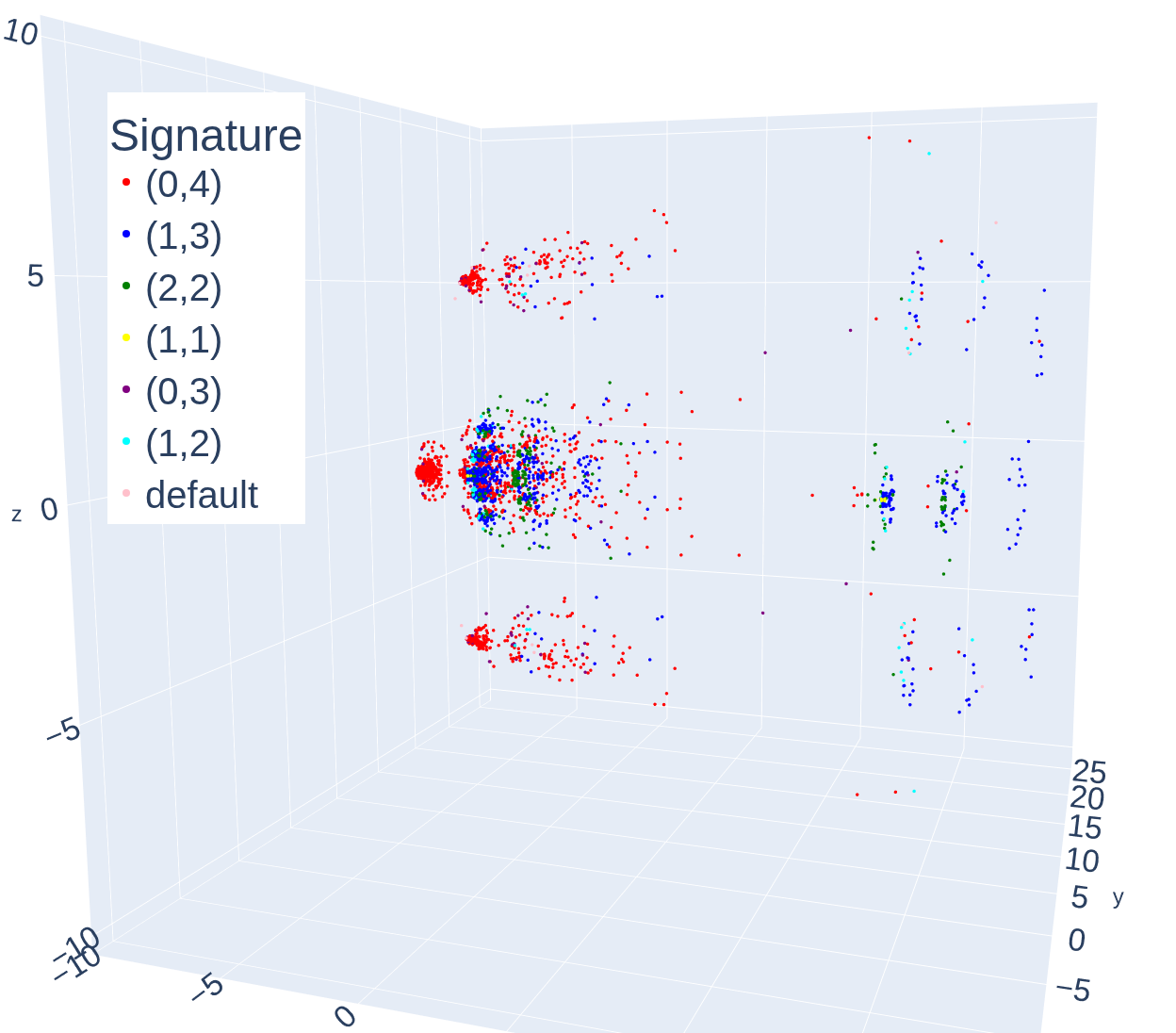
Stone pairings facilitate the definition of a feature space representing equational theories, where each dimension corresponds to the evaluation of a pairing on a Stone space. Crucially, this feature space can be reduced in dimensionality to a Latent Space while preserving key relationships between theories. This reduction is achieved by representing each theory not by the full vector of pairing evaluations, but by a lower-dimensional projection that captures the most significant variations in behavior. The resulting Latent Space allows for efficient comparison and analysis of equational theories based on their structural properties, effectively mapping complex relationships into a more manageable and interpretable form. The dimensions of this Latent Space represent principal components derived from the original feature space, capturing the directions of greatest variance in theory behavior.

Principal Component Analysis (PCA) is applied to the latent space of equational theories to facilitate both visualization and quantitative analysis. By reducing the dimensionality of the space while preserving variance, PCA enables the projection of high-dimensional theory representations onto a lower-dimensional subspace, typically two or three dimensions, suitable for plotting. Empirical results demonstrate that theories proven to be equivalent – meaning they satisfy the same equations – consistently cluster in close proximity within this reduced space. The tightness of these clusters provides a visual and measurable indication of the degree of similarity between theories, offering a means to assess equivalence and compare the relative complexity of different equational systems.

Unveiling the Essence: Features and Insights

The inherent complexity of equational theories – systems of equations and their logical consequences – isn’t simply a qualitative assessment, but a feature quantifiable through analysis of their ‘latent space’. Researchers have demonstrated that properties of ‘Stone pairings’ – a fundamental concept in logic connecting syntax and semantics – can serve as effective metrics. Specifically, the expectation and variance of these pairings within a theory reveal crucial information about its structure; a higher variance suggests a more diverse and potentially intricate set of relationships, while expectation indicates a central tendency in the theory’s logical consequences. This approach moves beyond intuitive judgements of complexity, offering a rigorous, data-driven means to compare and contrast different equational theories and understand the landscape of formal systems with increasing precision.

The complexity of an equational theory isn’t simply about the number of equations it contains, but rather how intricately those equations interrelate – a nuance captured by its ‘Signature’. This metric moves beyond simple counting by quantifying the structural richness of the theory, providing a more granular understanding of its expressive power and potential for computational difficulty. A higher Signature value indicates a more complex landscape of logical consequences, suggesting a greater challenge in tasks like theorem proving or model checking. Researchers are leveraging this measure to map the space of equational theories, identifying regions of high and low complexity, and ultimately gaining insights into the inherent limits of equational reasoning itself. By analyzing the Signature, it becomes possible to predict the difficulty of solving problems within a given theory and to develop more efficient algorithms for automated reasoning.

The Implication Preorder, a fundamental structure in equational theory, reveals nuanced relationships through the lens of atomic, reversible, and strict implications. Analysis demonstrates that reversible implications, representing a specific type of logical consequence, exhibit significantly shorter average edge lengths – just 0.69 – within this preorder. This contrasts sharply with atomic implications, averaging 5.29, and strict implications, which reach an average of 7.17. The substantial difference in edge length suggests that reversible implications represent a more tightly constrained and localized form of dependency within the theory, offering a quantifiable measure of how directly one equation follows from another and providing insight into the inherent structure and complexity of the equational system itself.

The pursuit of a ‘latent space’ for equational theories, as detailed in the paper, feels remarkably akin to distilling essence from complexity. One might observe, as Ken Thompson famously stated, “Sometimes it’s better to keep the whole thing simple.” The authors navigate a dense landscape of implication graphs and finite model theory, attempting to map reasoning flows into a geometrically interpretable space. It’s a bold endeavor-reducing abstract logical relationships to quantifiable dimensions-and the success hinges on a ruthless commitment to parsimony. They aren’t simply adding layers of abstraction; they’re actively seeking what can be removed without losing the core truth, a hallmark of mature design. The elegance lies not in what’s included, but in what’s left out.

Further Directions

The construction detailed herein offers a topology, not a terminus. The latent space, while demonstrably revealing of equational theory structure, remains a high-dimensional artifact. Future work must address dimensionality reduction-not merely as a computational convenience, but as a means of discerning genuinely salient features of logical consequence. The current reliance on Stone pairing, while elegant, presents a bottleneck. Alternative encodings, perhaps leveraging advances in graph neural networks, warrant exploration.

A persistent question concerns scalability. While the methodology functions on theories of moderate complexity, its application to large, industrial-strength equational systems – those governing, for instance, hardware verification or compiler optimization – remains unproven. A successful extension would require a shift from exhaustive enumeration towards approximation techniques, accepting a degree of imprecision in exchange for tractability.

Ultimately, the value of this work lies not in the latent space itself, but in the possibility of treating logical reasoning as a geometric phenomenon. To fully realize this potential requires a blurring of boundaries-between logic, statistics, and machine learning-and a willingness to abandon the pretense of absolute truth in favor of useful approximations.

---

Original article: https://arxiv.org/pdf/2601.20759.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

• Best Controller Settings for ARC Raiders

• Ashes of Creation Rogue Guide for Beginners

• Donkey Kong Country Returns HD version 1.1.0 update now available, adds Dixie Kong and Switch 2 enhancements

• Sega Insider Drops Tease of Next Sonic Game

• DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]

• 32 Kids Movies From The ’90s I Still Like Despite Being Kind Of Terrible

• Neverness to Everness ‘Co-Ex Test’ sign-ups now available

• 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)

• Fantasista Asuka launches February 12

• The Festive Pottery Throw Down 2025 line-up: Meet the celebrities

2026-01-29 12:39