Neutrino Secrets at the Quantum Limit

Author: Denis Avetisyan

A new analysis reveals the fundamental precision limits for measuring neutrino properties and uncovering the origins of matter-antimatter asymmetry.

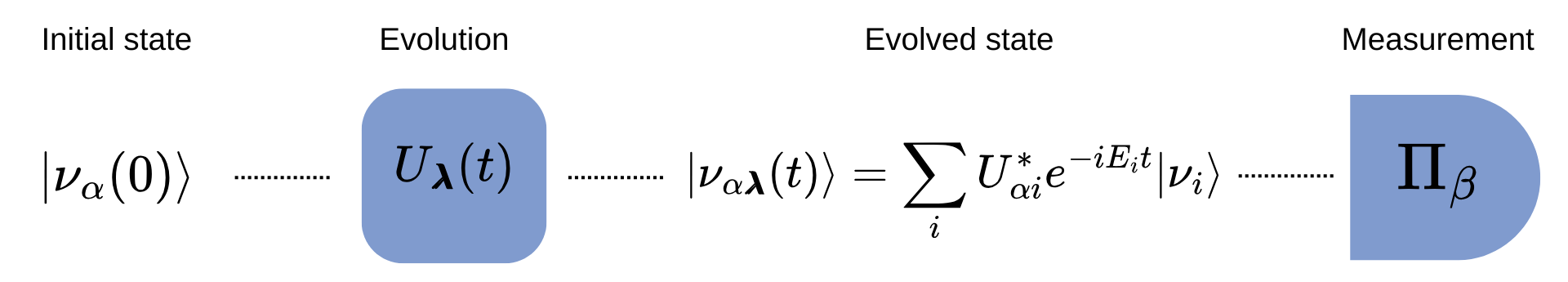
Neutrino flavor evolution, governed by parameters <span class="katex-eq" data-katex-display="false">\bf{\lambda}</span>, transforms a prepared neutrino state into a superposition of eigenstates, enabling a quantum metrology protocol where final flavor detection reveals insights into the oscillation process over time <span class="katex-eq" data-katex-display="false">t</span>. — Neutrino flavor evolution, governed by parameters $\bf{\lambda}$ , transforms a prepared neutrino state into a superposition of eigenstates, enabling a quantum metrology protocol where final flavor detection reveals insights into the oscillation process over time $t$ .

Quantum estimation theory is applied to neutrino oscillation experiments to determine optimal strategies for measuring mixing parameters and CP violation.

Despite ongoing advancements in precision measurements, fundamental limits on determining neutrino properties remain elusive. In ‘Quantum Estimation Theory Limits in Neutrino Oscillation Experiments’, we employ quantum metrology to investigate the ultimate precision achievable in extracting the parameters governing neutrino oscillations, focusing on the information content of currently accessible flavor measurements. Our analysis reveals that while these measurements approach optimality for determining mixing angles, the sensitivity to CP violation is intrinsically limited and significantly lower, though not yet constrained by experimental uncertainties. Can strategic experimental designs and future facilities overcome these quantum bounds and unlock a more complete understanding of neutrino properties and the matter-antimatter asymmetry in the universe?

The Elusive Nature of Neutrino Mass

For decades, neutrinos were theorized to be massless particles, traveling at the speed of light. However, experiments beginning in the late 20th century revealed a surprising phenomenon: neutrino oscillation. This peculiar behavior involves neutrinos changing “flavor” – morphing between electron, muon, and tau types – as they travel. Such transformations are only possible if neutrinos possess mass, albeit incredibly small. This discovery fundamentally altered the Standard Model of particle physics, which originally predicted neutrinos to be massless. The observation of neutrino oscillation provides compelling evidence that the Standard Model is incomplete, and necessitates further investigation into the nature of these elusive particles and the potential for physics beyond what is currently understood. The implication is that neutrinos aren’t simply elementary particles, but may have complex properties and interactions yet to be fully unveiled.

The phenomenon of neutrino oscillation isn’t merely a curious observation, but a pivotal key to a complete understanding of the universe’s fundamental building blocks. For decades, the Standard Model of particle physics – the prevailing theory describing known particles and forces – predicted neutrinos to be massless. However, experimental evidence of neutrino oscillation definitively demonstrates that neutrinos do possess mass, necessitating an extension to the Standard Model. This extension isn’t simply a patch; it opens pathways to explore physics beyond our current comprehension. Understanding the precise mechanisms driving this oscillation – including the subtle differences in neutrino types and their mixing – could reveal the origins of matter-antimatter asymmetry in the universe, hint at the existence of sterile neutrinos, and potentially connect to other unresolved mysteries like dark matter. Therefore, continued investigation into neutrino oscillation isn’t just about confirming existing theories, but about forging a new, more complete picture of reality.

Determining the precise values of parameters governing neutrino oscillation presents a substantial challenge to modern physics, demanding both ingenious experimental designs and sophisticated theoretical models. While the mixing angles – which describe the probability of a neutrino changing ‘flavor’ – have been relatively well constrained, estimating the CP-violating phase $\delta_{CP}$ remains significantly more difficult. This phase is crucial because it hints at an asymmetry between matter and antimatter, a key discrepancy in understanding the universe’s evolution. Experiments such as long-baseline neutrino oscillation setups and those utilizing intense neutrino beams are continually refined to amass sufficient data and reduce uncertainties in $\delta_{CP}$ measurements, pushing the boundaries of detector technology and data analysis techniques in the quest to reveal this fundamental aspect of neutrino behavior and its implications for physics beyond the Standard Model.

Fisher information (FI) for idealized flavor measurement, calculated for muon (anti)neutrino beams as a function of L/E, reveals sensitivity to <span class="katex-eq" data-katex-display="false"> \theta_{23} </span> and <span class="katex-eq" data-katex-display="false"> \theta_{13} </span> parameters, with variations observed under different <span class="katex-eq" data-katex-display="false"> \delta_{CP} </span> values and for experimental setups corresponding to T2K/T2HK (L=295 km, 0.6 GeV) and ESSνSB (L=360 km, 0.25 GeV), as compared to the quantum Fisher information (QFI). — Fisher information (FI) for idealized flavor measurement, calculated for muon (anti)neutrino beams as a function of L/E, reveals sensitivity to $\theta_{23}$ and $\theta_{13}$ parameters, with variations observed under different $\delta_{CP}$ values and for experimental setups corresponding to T2K/T2HK (L=295 km, 0.6 GeV) and ESSνSB (L=360 km, 0.25 GeV), as compared to the quantum Fisher information (QFI).

Mapping the Neutrino Mixing Matrix

The Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix, analogous to the Cabibbo-Kobayashi-Maskawa (CKM) matrix for quarks, is a 3×3 unitary matrix that describes the probability amplitudes for a neutrino of a specific flavor (electron, muon, or tau) to oscillate into another flavor. This matrix contains four independent parameters: three mixing angles $\theta_{12}$ , $\theta_{13}$ , and $\theta_{23}$ , and one CP-violating phase $\delta_{CP}$ . Additionally, the mass-squared differences $\Delta m_{21}^2$ and $\Delta m_{32}^2$ are required to fully characterize neutrino oscillation, though these are not elements within the PMNS matrix itself. The PMNS matrix therefore provides a complete mathematical framework for understanding and predicting neutrino oscillation probabilities, linking flavor eigenstates to mass eigenstates and quantifying the degree of mixing.

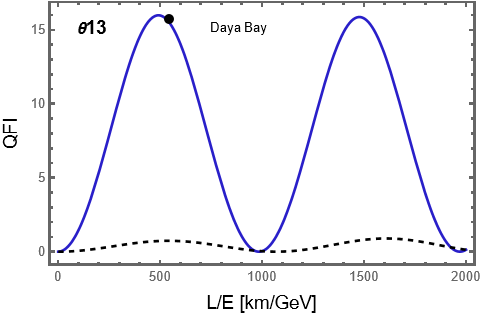
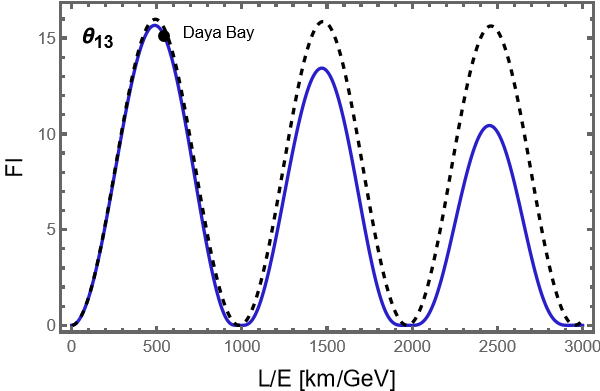
Reactor experiments, prominently exemplified by Daya Bay, determine neutrino mixing angles by monitoring the flux of electron antineutrinos produced in nuclear reactor fission. These experiments leverage the well-understood characteristics of reactor $\overline{\nu}_e$ emission and utilize segmented detectors to measure the energy spectrum of the antineutrinos. By precisely measuring the rate of disappearance of $\overline{\nu}_e$ as a function of distance from the reactor core, these experiments can extract the mixing angle $\theta_{13}$ with high statistical significance. The relatively clean signal and systematic uncertainties associated with reactor antineutrino fluxes contribute to the precision achieved in these measurements, providing critical input for the global analysis of neutrino oscillation parameters.

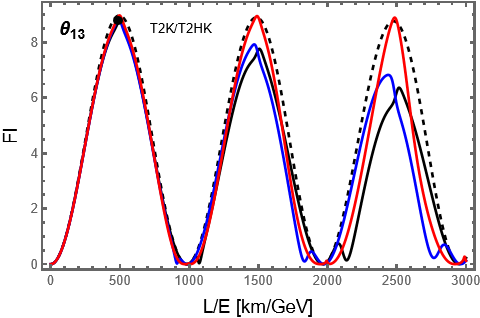
Long-baseline neutrino experiments, notably T2K and the proposed Hyper-Kamiokande (T2HK), utilize beams primarily composed of muon neutrinos to investigate Charge-Parity (CP) violation in the leptonic sector. CP violation manifests as a difference in the oscillation probabilities of neutrinos versus antineutrinos. Measuring the CP-violating phase, $\delta_{CP}$ , is statistically more difficult with muon neutrino beams compared to electron neutrino beams. This is because the initial muon neutrino beam is produced from pion decay, and subsequent neutrino interactions in the far detector are less sensitive to $\delta_{CP}$ than the electron appearance channel observed in reactor experiments; therefore, significantly larger detector exposures and higher beam intensities are required to achieve comparable statistical precision in determining $\delta_{CP}$ .

The sensitivity to <span class="katex-eq" data-katex-display="false"> heta_{12}</span> (a) and <span class="katex-eq" data-katex-display="false"> heta_{13}</span> (b) for an electron antineutrino beam is shown, with oscillation probability (multiplied by 5 in a and 15 in b) overlaid for KamLAND (180 km, 3.6 MeV) and Daya Bay (1.64 km, 3 MeV) reactor experiments. — The sensitivity to $heta_{12}$ (a) and $heta_{13}$ (b) for an electron antineutrino beam is shown, with oscillation probability (multiplied by 5 in a and 15 in b) overlaid for KamLAND (180 km, 3.6 MeV) and Daya Bay (1.64 km, 3 MeV) reactor experiments.

The Limits of Precision: A Quantum Perspective

Quantum Estimation Theory (QET) is a mathematical formalism used to calculate the fundamental limits of precision with which parameters governing a quantum system can be estimated. Unlike classical estimation where precision is limited by statistical fluctuations and noise, QET leverages the principles of quantum mechanics – superposition and entanglement – to determine the maximum possible information obtainable from a given quantum state about an unknown parameter. This is achieved by defining quantities, such as the Quantum Fisher Information $F_Q$ , which quantify the sensitivity of the quantum state to infinitesimal changes in the parameter being estimated. The resulting bounds, like the Cramer-Rao Bound, provide a benchmark against which experimental precision can be evaluated, and guide the development of optimal measurement strategies to approach these theoretical limits.

The Quantum Fisher Information (QFI) serves as the theoretical upper bound on the precision achievable when estimating a parameter. It quantifies the maximum amount of information about that parameter that can be extracted from a given quantum state. In the context of neutrino oscillation parameters, the QFI for $\theta_{23}$ is approximately 15, indicating a significantly higher potential precision compared to the parameter $\delta_{CP}$ . This disparity demonstrates that, theoretically, $\theta_{23}$ can be determined with substantially greater accuracy than $\delta_{CP}$ using optimal quantum measurement strategies; however, experimental limitations will invariably result in precision values below these QFI limits.

The Cramer-Rao Bound (CRB) is a fundamental limit in parameter estimation, mathematically derived from the Fisher Information. Specifically, the CRB states that the variance of any unbiased estimator of a parameter is lower bounded by the inverse of the Fisher Information; expressed as $Var(\hat{\theta}) \ge \frac{1}{I(\theta)}$ , where $\hat{\theta}$ is the estimator and $I(\theta)$ represents the Fisher Information. This bound is crucial because it defines the best possible precision achievable by any estimator, regardless of its complexity. Consequently, the CRB serves as a benchmark against which the performance of practical estimators can be evaluated, allowing researchers to determine how close experimental measurements are to the theoretical limits of precision and guiding the development of improved estimation strategies.

The classical effective Fisher information for flavor detection, <span class="katex-eq" data-katex-display="false">F_{\\nu,\\overline{\\nu}}(\\delta_{CP})</span>, varies with <span class="katex-eq" data-katex-display="false">\delta_{CP}</span> and is maximized when optimized over the first oscillation period (black solid curve), while peaks in the second oscillation period (blue dash-dotted curve) show reduced sensitivity compared to evaluation at the first peak (red long-dashed curve). — The classical effective Fisher information for flavor detection, $F_{\\nu,\\overline{\\nu}}(\\delta_{CP})$ , varies with $\delta_{CP}$ and is maximized when optimized over the first oscillation period (black solid curve), while peaks in the second oscillation period (blue dash-dotted curve) show reduced sensitivity compared to evaluation at the first peak (red long-dashed curve).

Beyond Point-Like Particles: The Future of Neutrino Physics

Conventional descriptions of neutrinos often treat them as point-like particles with definite momenta, yet the very nature of quantum mechanics dictates an inherent uncertainty in these properties – a spread described by a wave packet. Recent theoretical work demonstrates that accurately modeling neutrinos as these extended wave packets is crucial for resolving decoherence effects arising from neutrino propagation and interactions. These effects, previously neglected in many precision measurements, can subtly alter oscillation probabilities and introduce systematic errors. By incorporating wave packet descriptions, researchers can significantly improve the accuracy of experiments designed to probe fundamental neutrino properties, such as masses, mixing angles, and $CP$ violation. This refined approach ensures that experimental results more faithfully reflect the underlying physics, pushing the boundaries of what can be learned from these elusive particles.

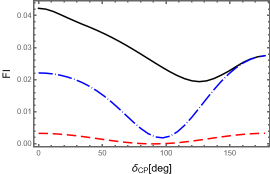
The forthcoming European Spallation Source neutrino facility (ESSνSB) represents a significant leap forward in the pursuit of understanding charge-parity (CP) violation in the neutrino sector. This next-generation facility will utilize an unprecedented 5 MW proton beam impinging on a target, generating an intense neutrino beam. Innovative technologies, including a highly efficient target station and a novel horn system, are being developed to maximize neutrino flux and beam purity. These advancements will allow ESSνSB to probe neutrino oscillations with exceptional precision, specifically targeting the second oscillation maximum where sensitivity to the $\delta_{CP}$ parameter – a crucial component in explaining the matter-antimatter asymmetry in the universe – is optimized. By dramatically increasing the statistics available for neutrino interaction measurements, ESSνSB promises to either confirm or refute current theoretical models and potentially unveil new physics beyond the Standard Model.

Current investigations into neutrino oscillation-the process by which these elusive particles change “flavor”-seek to precisely determine the parameter $\delta_{CP}$ , a crucial component in explaining the observed matter-antimatter asymmetry in the universe. Achieving this requires a synergistic approach, pairing sophisticated theoretical frameworks with next-generation experimental facilities like the European Spallation Source neutrino facility (ESSνSB). Importantly, focusing measurements on the second oscillation maximum-a point where neutrino oscillation probabilities exhibit heightened sensitivity-promises to significantly amplify the ability to discern $\delta_{CP}$ . This strategy allows researchers to overcome inherent limitations in current data and potentially resolve long-standing mysteries surrounding neutrino properties and their role in shaping the cosmos, ultimately providing insights into why matter dominates over antimatter in the observable universe.

Reactor experiments probing an electron antineutrino beam reveal the distributions of <span class="katex-eq" data-katex-display="false">F_{\overline{\nu}_{e}}(\theta_{12})</span> and <span class="katex-eq" data-katex-display="false">H_{\overline{\nu}_{e}}(\theta_{12})</span> (a) and <span class="katex-eq" data-katex-display="false">F_{\overline{\nu}_{e}}(\theta_{13})</span> and <span class="katex-eq" data-katex-display="false">H_{\overline{\nu}_{e}}(\theta_{13})</span> (b) when <span class="katex-eq" data-katex-display="false">\delta_{CP} = \delta_{CP}^{(\mathrm{NO})}</span>. — Reactor experiments probing an electron antineutrino beam reveal the distributions of $F_{\overline{\nu}_{e}}(\theta_{12})$ and $H_{\overline{\nu}_{e}}(\theta_{12})$ (a) and $F_{\overline{\nu}_{e}}(\theta_{13})$ and $H_{\overline{\nu}_{e}}(\theta_{13})$ (b) when $\delta_{CP} = \delta_{CP}^{(\mathrm{NO})}$ .

The pursuit of precision in neutrino oscillation experiments, as detailed in the study, highlights a familiar tension: the limits imposed by inherent uncertainty. One might observe that, as Mary Wollstonecraft stated, “It is time to try the method of reason.” This isn’t simply a call for logical thought, but an acknowledgment that any measurement, even one employing the sophisticated tools of quantum metrology, is subject to bounds – the Cramér-Rao bound being a prime example. The paper demonstrates that while flavor measurements approach these theoretical limits, discerning CP violation-a key to understanding matter-antimatter asymmetry-demands a more nuanced approach. The design of experiments, therefore, isn’t about finding truth, but about strategically minimizing the scope of potential falsehood, iteratively refining models against observed data.

Where Do We Go From Here?

The application of quantum estimation theory, as demonstrated, reveals a somewhat predictable truth: parameter estimation isn’t simply about collecting more data. It’s about how that data is collected. While current experimental designs appear reasonably efficient for determining neutrino mixing angles – approaching the fundamental limits dictated by the Cramér-Rao bound – the pursuit of CP violation measurements exposes a starker reality. Achieving precision isn’t a matter of incremental improvement, but of fundamentally rethinking experimental strategies. The notion that simply increasing exposure will solve the problem is, statistically speaking, naive.

Future work must move beyond idealized scenarios. The analysis hinges on precise knowledge of systematic uncertainties, an assumption rarely met in practice. A thorough investigation of how realistic detector effects – energy resolution, acceptance, and misidentification rates – degrade performance is crucial. Furthermore, the emphasis on specific oscillation peaks suggests a potential trade-off; optimizing for CP violation might necessitate sacrificing precision in other parameters. A holistic optimization, accounting for the interplay between all relevant observables, remains a significant challenge.

Ultimately, the utility of these theoretical limits resides not in their attainment – a feat unlikely given the complexities of real-world experiments – but in their power to guide experimental design. If a claimed measurement exceeds these bounds, skepticism is warranted. Replication, as always, will be the ultimate arbiter. The pursuit of neutrino properties, it seems, will continue to be a testament to the enduring tension between theoretical elegance and experimental messiness.

Original article: https://arxiv.org/pdf/2602.16534.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

The Elusive Nature of Neutrino Mass

Mapping the Neutrino Mixing Matrix

The Limits of Precision: A Quantum Perspective

Beyond Point-Like Particles: The Future of Neutrino Physics

Where Do We Go From Here?

See also: