Quantum Magic’s Reach: How Resources Spread Through Complex Systems

by

Author: Denis Avetisyan

New research reveals the mechanisms governing the propagation of quantum ‘magic’-a vital resource for computation-within systems governed by specific dynamics.

The growth of magic-quantified by $W(t)$-under random brickwork Clifford circuits demonstrates a consistent relationship with entanglement and operator spreading velocities, exhibiting an upper bound defined by [Eq. (S10)] and remaining unaffected by boundary conditions or specific unitary choices within the studied architecture, as evidenced by analysis across $10^2$ circuit realizations with negligible error.
The growth of magic-quantified by $W(t)$-under random brickwork Clifford circuits demonstrates a consistent relationship with entanglement and operator spreading velocities, exhibiting an upper bound defined by [Eq. (S10)] and remaining unaffected by boundary conditions or specific unitary choices within the studied architecture, as evidenced by analysis across $10^2$ circuit realizations with negligible error.

This study establishes bounds on the rate of magic dissemination under unitary Clifford dynamics, linking its spread to both entanglement growth and operator spreading.

Quantifying and controlling quantum resources remains a central challenge in realizing fault-tolerant quantum computation, despite the conserved nature of ‘magic’-a non-stabilizer property vital for universal quantum computation. In ‘Magic spreading under unitary Clifford dynamics’, we investigate the spatiotemporal dynamics of locally injected magic within Clifford circuits, revealing a ballistic spreading governed by entanglement velocity. Through a bipartite magic gauge, we establish operationally relevant length scales characterizing magic delocalization and rigorously demonstrate how these scales bound its dissemination rate. How might understanding this interplay between magic, entanglement, and operator spreading inform the development of more robust quantum error correction strategies and unlock deeper insights into quantum many-body dynamics?

The Fragility of Quantum Advantage

Quantum computation’s potential surpasses what can be achieved through entanglement alone; while entanglement facilitates correlations between qubits, it’s insufficient for creating the full range of quantum operations needed for universal computation. This necessitates the introduction of ‘magic states’, highly non-classical states-like the $T$ state-that effectively allow for the implementation of non-Clifford gates. These gates, unlike Clifford gates, cannot be efficiently simulated on classical computers and are essential for achieving quantum speedup. Without these magic states, a quantum computer is limited to tasks that a classical computer could perform with similar resources, thus hindering its power. The creation, preservation, and manipulation of these states represent a significant challenge in building practical, fault-tolerant quantum computers, as they are inherently fragile and susceptible to noise.

Quantum error correction, a cornerstone of practical quantum computing, typically employs stabilizer codes to shield fragile quantum information from environmental noise. However, these codes, while effective at correcting errors that arise from simple bit flips or phase flips, fundamentally struggle with the creation and manipulation of magic states – essential quantum states required for universal quantum computation. The very nature of stabilizer codes-their reliance on commuting operators-prevents them from efficiently implementing the non-Clifford gates needed to generate these magic states, creating a bottleneck in scaling quantum computers. This limitation isn’t a matter of simply adding more qubits; it’s an inherent constraint of the error correction scheme itself, forcing researchers to explore alternative approaches that can propagate and utilize magic states without sacrificing fault tolerance, such as incorporating dedicated hardware or novel encoding strategies.

The pursuit of scalable, fault-tolerant quantum computation faces a significant hurdle: the efficient implementation of universal quantum operations requires resources beyond simple entanglement – specifically, ‘magic states’. While stabilizer codes excel at protecting quantum information from common errors, they prove inadequate for manipulating these crucial magic states without destroying the very properties that make them powerful. This limitation directly impedes the ability to build larger, more complex quantum computers, as the resources needed to prepare and process magic states grow rapidly with system size. Consequently, a substantial body of research is now focused on developing novel techniques – including methods to distill, propagate, and efficiently utilize magic – to overcome this bottleneck and unlock the full potential of quantum computation.

Unitary distillation concentrates magic from a pure state by applying a Clifford unitary to a subsystem and an external system, resulting in a magic state on the external system.
Unitary distillation concentrates magic from a pure state by applying a Clifford unitary to a subsystem and an external system, resulting in a magic state on the external system.

Beyond Entanglement: Characterizing Quantum Magic

Quantum magic, as a resource, is fundamentally defined by non-Gaussianity, a property distinguishing quantum states from those describable by classical probability distributions. Gaussian states represent the maximum amount of correlations achievable with classical resources; therefore, any deviation from Gaussianity indicates the presence of genuinely quantum features. Specifically, non-Gaussianity signifies correlations that cannot be replicated through classical means, and it is this departure from classicality that enables tasks impossible with classical systems. The degree of non-Gaussianity is quantifiable and directly relates to the amount of ‘magic’ present in a quantum state, effectively serving as a signature for its quantum advantage. States exhibiting non-Gaussianity necessarily possess some degree of quantumness beyond simple entanglement, allowing for the exploration of resources unavailable in classical computation and communication.

Linear magic length provides a quantifiable metric for the spatial range of non-classical correlations, specifically ‘magic’, within a quantum system. This length is determined by identifying the maximum distance over which a state’s magic remains demonstrably non-zero; beyond this distance, the influence of the magic diminishes to a negligible level. Calculation involves analyzing the decay of magic as a function of spatial separation, typically achieved through partitioning the system and assessing the remaining magic in each subsystem. A larger linear magic length indicates a greater capacity for influencing spatially separated components, implying a more robust and extended form of non-classicality, while a shorter length suggests a localized effect. This measure is crucial for understanding the practical limitations of utilizing magic for quantum information processing tasks, where spatial distribution and connectivity are key considerations.

Rényi entropy, a generalization of the von Neumann entropy, provides a quantifiable measure of entanglement beyond the limitations of characterizing only pure states. Specifically, it allows for the assessment of entanglement in mixed states commonly encountered alongside ‘magic’ – non-Gaussian correlations. The $R_{\alpha}$ Rényi entropy, calculated as $R_{\alpha} = \frac{1}{1-\alpha} \log_{2} Tr(\rho^{\alpha})$, where $\rho$ is the density matrix and $\alpha$ is a positive real number, offers a parameterizable approach to detecting and quantifying entanglement even when traditional entanglement measures fail. Analysis of Rényi entropy alongside metrics for ‘magic’ reveals whether the observed non-Gaussianity arises solely from entanglement or represents a genuinely distinct resource, thereby clarifying the relationship and potential separability of these quantum properties.

Magic length scales are determined by the extent of mutually-irreducible, minimal-length subsystems from which magic can be extracted from a quantum state.
Magic length scales are determined by the extent of mutually-irreducible, minimal-length subsystems from which magic can be extracted from a quantum state.

Simulating the Flow of Magic and Quantum Chaos

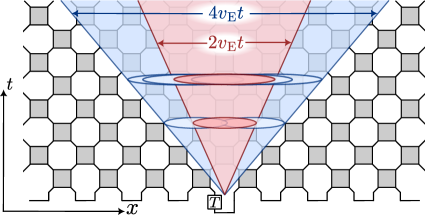
The self-dual kicked Ising circuit (SDKIFCircuit) serves as a computationally feasible model for investigating the propagation of magic in quantum systems. This circuit, a driven, discrete-time quantum system, exhibits characteristics allowing for analytical and numerical study of out-of-equilibrium dynamics. Its self-duality simplifies calculations and provides a robust framework for tracking the spread of non-conservation laws – represented here as ‘magic’ – within the system. Specifically, the SDKIFCircuit allows researchers to observe and quantify how initial localized magic disperses over time, facilitating the measurement of key velocities like the butterfly and entanglement velocities that govern its propagation. The tractability of the SDKIFCircuit, compared to more complex systems, makes it an ideal platform for validating theoretical predictions about the dynamics of magic and its relationship to quantum chaos.

Simulations of the self-dual kicked Ising circuit demonstrate the propagation of magic, quantified by the evolution of linear magic length, denoted as $W(t)$. Analysis indicates that the growth of this linear magic length is not unbounded, and is constrained by the combined rates of information dispersal and entanglement. Specifically, the simulations show that $W(t) ≤ 2(v_Bt + 2v_Et)$, where $v_B$ represents the butterfly velocity and $v_E$ represents the entanglement velocity. This inequality establishes an upper limit on the rate at which magic can spread within the modeled system, linking it directly to the velocities of these two fundamental quantum processes.

The propagation of magic within the self-dual kicked Ising circuit is directly linked to the principles of quantum chaos, specifically through the concept of the butterfly velocity ($v_B$). This velocity quantifies the rate at which initial perturbations, or information – and consequently, magic – disperse throughout the system. The maximum velocity at which magic can spread, denoted as $v_{W_{max}}$, is fundamentally constrained by the butterfly velocity and the entanglement velocity ($v_E$), and is mathematically defined as $v_{W_{max}} = v_B + 2v_E$. This relationship indicates that the entanglement velocity contributes to the overall spread, effectively doubling its influence on the maximum achievable velocity of magic propagation beyond the initial dispersal rate dictated by the butterfly velocity.

In a noisy quantum circuit, injected magic spreads at the entanglement velocity, defining a region beyond which further operations cannot reduce quantum resourcefulness, with the boundary of this region expanding at twice that velocity.
In a noisy quantum circuit, injected magic spreads at the entanglement velocity, defining a region beyond which further operations cannot reduce quantum resourcefulness, with the boundary of this region expanding at twice that velocity.

Architecting for Magic: Circuit Design and Quantum Advantage

Unitary Clifford circuits represent a cornerstone in the effort to simulate quantum systems, providing a relatively simple framework for exploring quantum dynamics. However, these circuits possess an inherent limitation: they struggle to generate and sustain what physicists refer to as ‘magic’ – the ability to perform computations that are impossible for classical computers. This deficiency stems from the circuits’ restricted set of allowed operations, which prevents them from fully exploiting the potential of quantum superposition and entanglement. While capable of modeling certain quantum phenomena, the inability to reliably create and maintain ‘magic’ ultimately restricts the computational power achievable with purely Clifford-based circuits, motivating research into methods for augmenting their capabilities and unlocking more complex quantum simulations.

The capacity of unitary Clifford circuits to perform complex quantum simulations is fundamentally limited by their ability to sustain ‘magic’ – the non-classical resources crucial for quantum speedup. Researchers have discovered that strategically inserting identity gates – operations that do nothing to the quantum state – into these circuits can surprisingly enhance their magical capabilities. This ‘identity doping’ effectively alters the circuit’s structure, creating pathways that allow magic to be generated and preserved for longer durations. By carefully controlling the placement and density of these identity gates, it becomes possible to bolster the circuit’s resilience against decoherence and error, leading to more robust and powerful quantum computations. The process doesn’t introduce new resources, but rather optimizes the existing ones, demonstrating a novel method for extracting greater computational potential from established quantum architectures.

The efficiency with which quantum computations can be performed hinges on the rate at which logical operators – the building blocks of quantum algorithms – shrink during processing. Researchers have identified a critical timescale, denoted as $t^ = L/(2v_{W_{max}}) = L/(6v_E)$, which governs this dynamic. This timescale represents a threshold; when operations occur faster than $t^$, the system’s ability to harness and propagate ‘magic’ – the resource enabling quantum speedup – significantly improves. Essentially, exceeding this rate allows for more robust and efficient quantum information processing, as the delicate quantum states required for computation are better preserved and manipulated, ultimately enhancing computational power and opening pathways to more complex algorithms. Understanding and optimizing operations relative to this timescale is therefore paramount for building practical and scalable quantum computers.

Channel capacity, as a proxy for quantum magic preservation, remains near one for fill fractions up to 0.5 under random brickwork Clifford circuits with identity doping, but rapidly decays to zero beyond that threshold, indicating a loss of quantum coherence.
Channel capacity, as a proxy for quantum magic preservation, remains near one for fill fractions up to 0.5 under random brickwork Clifford circuits with identity doping, but rapidly decays to zero beyond that threshold, indicating a loss of quantum coherence.

The study meticulously charts how ‘magic’-a resource vital for universal quantum computation-disseminates through a quantum system, revealing a complex interplay between entanglement and operator growth. This propagation isn’t simply about distance, but rather how information-and the potential for computation-expands within the system’s structure. As Richard Feynman observed, “The difficulty lies not so much in developing new ideas as in escaping from old ones.” This sentiment resonates with the research, which challenges intuitive notions of locality and demonstrates how magic’s spread is governed by a dynamic, holistic process. The bounds established on magic dissemination aren’t limitations, but rather fundamental characteristics of the system’s architecture, echoing the principle that structure dictates behavior.

The Horizon of Magic

The study of magic’s dissemination, as presented, reveals a familiar truth: the propagation of any resource-information, energy, or, in this case, non-stabilizer states-is not merely a question of localized growth. It is a systemic process. One cannot simply inject ‘magic’ into a circuit without considering the entire architecture of entanglement and operator spread. Attempting to accelerate this propagation without understanding the constraints imposed by unitary dynamics is akin to attempting to enlarge a vein without fortifying the heart. The system will ultimately resist, and the resource will dissipate or become inaccessible.

Future work must address the interplay between these dynamics and the specific codes employed. Stabilizer codes, while offering a degree of protection, inherently limit the expression of magic. Exploring the boundaries of this limitation-the point at which code structure actively hinders the beneficial spread of non-stabilizer states-is crucial. Furthermore, the linear magic length, while a useful metric, offers only a snapshot of a potentially far more complex, non-linear reality.

The question, then, is not simply how to maximize the rate of magic spread, but how to sculpt the underlying structure to facilitate its natural flow. This requires a shift in perspective, from viewing quantum error correction as a shield against noise, to viewing it as a framework for resource management-a living architecture where the health of the whole dictates the vitality of its parts.

Original article: https://arxiv.org/pdf/2511.21487.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-11-29 20:29