Author: Denis Avetisyan
New research reveals that observing quantum systems can dramatically accelerate their natural tendency to restore symmetry, challenging conventional understandings of relaxation dynamics.
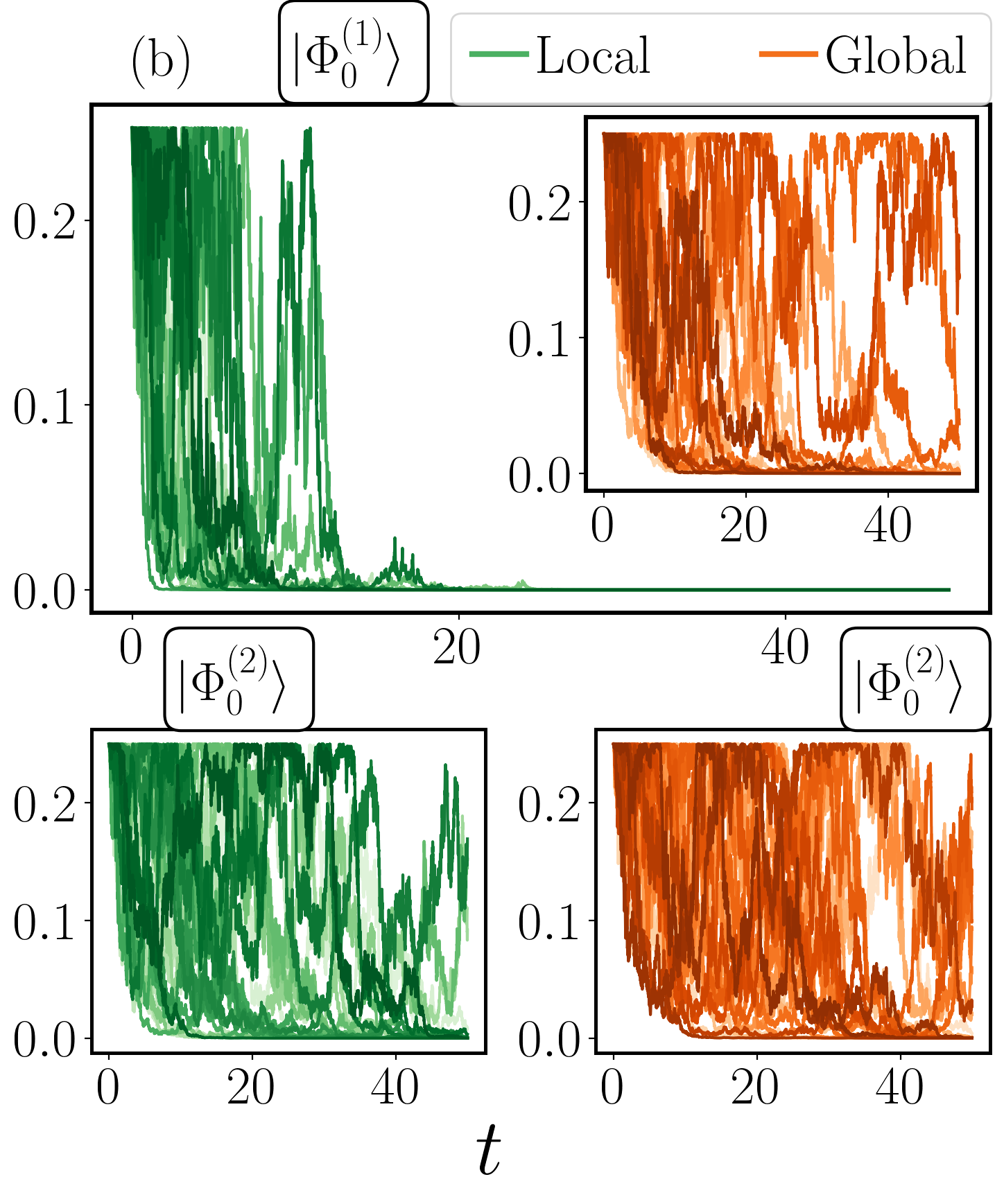
Continuous measurement of open quantum systems influences the timescale of U(1) symmetry restoration, with initial state and measurement type playing critical roles.
Relaxation dynamics in open quantum systems are often understood through the lens of global system properties, yet the role of measurement in shaping these dynamics remains nuanced. This work, ‘Measurement induced faster symmetry restoration in quantum trajectories’, investigates how continuous measurement can actively influence the restoration of U(1) symmetry in quantum trajectories, demonstrating that the timescale of symmetry restoration is state-dependent, with distant charge sectors relaxing faster. We find that local monitoring can further accelerate this process compared to global measurements, offering a potential pathway to control relaxation. Could strategically designed measurement schemes provide a means to engineer desired symmetry properties in complex quantum systems?
Quantum Entanglement: A System’s Delicate Dance with Observation
The inherent difficulty in modeling open quantum systems stems from the inescapable entanglement between the system of interest and its surrounding environment. Unlike isolated quantum entities, these systems continuously exchange energy and information, leading to decoherence – the loss of quantum properties like superposition and entanglement. Accurately capturing this dynamic interplay requires tracing over the environmental degrees of freedom, a computationally expensive and often intractable task. This leads to a proliferation of approximations, each with limitations that can significantly impact the fidelity of simulations and predictions. The challenge isn’t merely mathematical complexity; it’s a fundamental consequence of quantum mechanics, where observation – or, in this case, environmental interaction – fundamentally alters the system’s behavior. Consequently, a complete and accurate description of open quantum systems remains a central, ongoing pursuit in theoretical physics and quantum engineering.
Simulating the behavior of open quantum systems-systems that inevitably interact with their surroundings-presents a significant hurdle for physicists and engineers. Conventional methods for tackling this complexity frequently necessitate compromises; either the resulting simulations are computationally expensive, demanding prohibitive resources, or they employ approximations that diminish the reliability of the predicted outcomes. These approximations, while enabling progress, often involve simplifying the environment or the interaction between the system and its surroundings, potentially obscuring crucial details of the quantum dynamics. For instance, techniques like the Born-Markov approximation assume a weak system-environment coupling and short environmental correlation times, conditions not always met in realistic scenarios. Consequently, achieving both accuracy and computational feasibility remains a central challenge in the study of open quantum systems, impacting the development of quantum technologies and fundamental investigations into decoherence and dissipation.
The pursuit of mastering open quantum systems isn’t merely an academic exercise; it represents a critical pathway toward realizing the full potential of emerging quantum technologies. These systems, constantly interacting with-and therefore influenced by-their surroundings, underpin the functionality of proposed quantum computers, sensors, and communication networks. Accurate modeling of these interactions is essential to mitigate decoherence-the loss of quantum information-and to engineer robust, reliable devices. Beyond technological applications, a deeper understanding of open quantum systems also promises to resolve long-standing puzzles in fundamental physics, offering insights into the quantum-to-classical transition, the nature of measurement, and even the behavior of complex biological systems where quantum effects may play a significant role. The ability to predict and control these systems, therefore, holds the key to unlocking both groundbreaking technologies and a more complete picture of the universe itself.
Quantum Trajectories: Unraveling the System’s Hidden Pathways
The \text{QuantumTrajectory} method addresses the challenges of solving the \text{QuantumMasterEquation} by interpreting the equation’s probabilistic description as an ensemble of individual, time-dependent trajectories. Instead of calculating average system behavior directly, this approach simulates numerous possible quantum states evolving in time, each weighted by a probability derived from the master equation. Each trajectory represents a potential history of the system, conditioned on a specific measurement outcome at each time step. This unraveling allows for a detailed examination of the system’s dynamics, revealing information inaccessible through traditional master equation solutions that only provide population-level averages. The resulting trajectories are stochastic due to the inherent probabilistic nature of quantum mechanics and the continuous measurement process.
Continuous measurement, in the context of quantum mechanics, involves repeatedly measuring a system observable without collapsing the wavefunction entirely after each measurement. This differs from traditional, discrete measurements which provide only information about the system at specific times. By tracking the evolution of the system conditioned on the continuous stream of measurement results, researchers can gain access to detailed, real-time information about the system’s dynamics. This allows for analysis beyond ensemble-averaged behaviors, revealing fluctuations and correlations that would otherwise be obscured. The data obtained from continuous measurement is used to reconstruct the system’s wavefunction at each time step, providing a trajectory-based understanding of its evolution and enabling investigation of non-classical phenomena.
Implementation of continuous monitoring within the `QuantumTrajectory` method is achieved through techniques such as `QuantumStateDiffusion` and the `QuantumJumpProcess`. `QuantumStateDiffusion` represents the continuous measurement as a diffusion process in the space of density matrices, effectively updating the quantum state based on incoming information; this method does not exhibit abrupt changes in the wavefunction. Conversely, the `QuantumJumpProcess` models measurement as a series of instantaneous projections onto eigenstates of the measured observable, leading to discrete jumps in the wavefunction and accounting for the probabilistic nature of quantum measurement. Both techniques allow for the unraveling of the `QuantumMasterEquation` but differ in how they represent the continuous acquisition of information about the system.
The selection between GlobalMonitoring and LocalMonitoring in continuous measurement protocols is dictated by the properties of the observable being measured. GlobalMonitoring considers the entire system state when determining measurement outcomes, appropriate when the observable depends on correlations across the entire system. Conversely, LocalMonitoring focuses only on the portion of the system state directly interacting with the measurement apparatus, suitable for observables that are localized or depend only on a specific subsystem. This distinction impacts the form of the stochastic unraveling; GlobalMonitoring generally leads to more complex trajectories reflecting system-wide effects, while LocalMonitoring provides a simplified representation focused on the measured region, and is computationally less expensive.
Symmetry’s Dance: Breaking and Restoring Order in Quantum Realms
Quantum systems frequently possess symmetries, mathematically represented by operators that commute with the system’s Hamiltonian. A key example is the \hat{N} or `NumberOperator`, which corresponds to the conservation of particle number. These symmetries directly imply the existence of conserved quantities, such as total energy or particle number, and contribute to the system’s stability by restricting the possible states it can occupy. The eigenvalues of these symmetry operators define “number sectors” within the Hilbert space, effectively partitioning the system into distinct, non-interacting subspaces. Consequently, understanding these symmetry operators and their associated conserved quantities is crucial for predicting and analyzing the behavior of quantum systems.
External perturbations to a quantum system can induce \text{SymmetryBreaking}, a process where the initial symmetries of the system’s Hamiltonian are no longer conserved. These perturbations, which can take various forms such as applied fields or interactions with an external environment, modify the system’s energy landscape and alter its eigenstates. Consequently, quantities previously conserved, governed by symmetry operators like the \text{NumberOperator}, are no longer constant. This change in symmetry can manifest as alterations to the system’s physical properties, including its density profile, and can drive transitions to new, distinct quantum states. The extent and nature of the symmetry breaking are dependent on the strength and type of the applied perturbation, as well as the system’s inherent characteristics.
Continuous measurement of a quantum system can fundamentally alter its symmetry properties, leading to distinct phase transitions. Specifically, the PurificationTransition arises when measurement projects the system onto a subspace with reduced symmetry, effectively “purifying” a specific state. Conversely, the ZenoPhaseTransition occurs when frequent measurements effectively freeze the system’s evolution, stabilizing a particular state and altering its symmetry compared to free evolution. These transitions are not simply observations of pre-existing changes; the measurement process itself drives the symmetry alteration, demonstrating a strong interplay between observation and system dynamics.
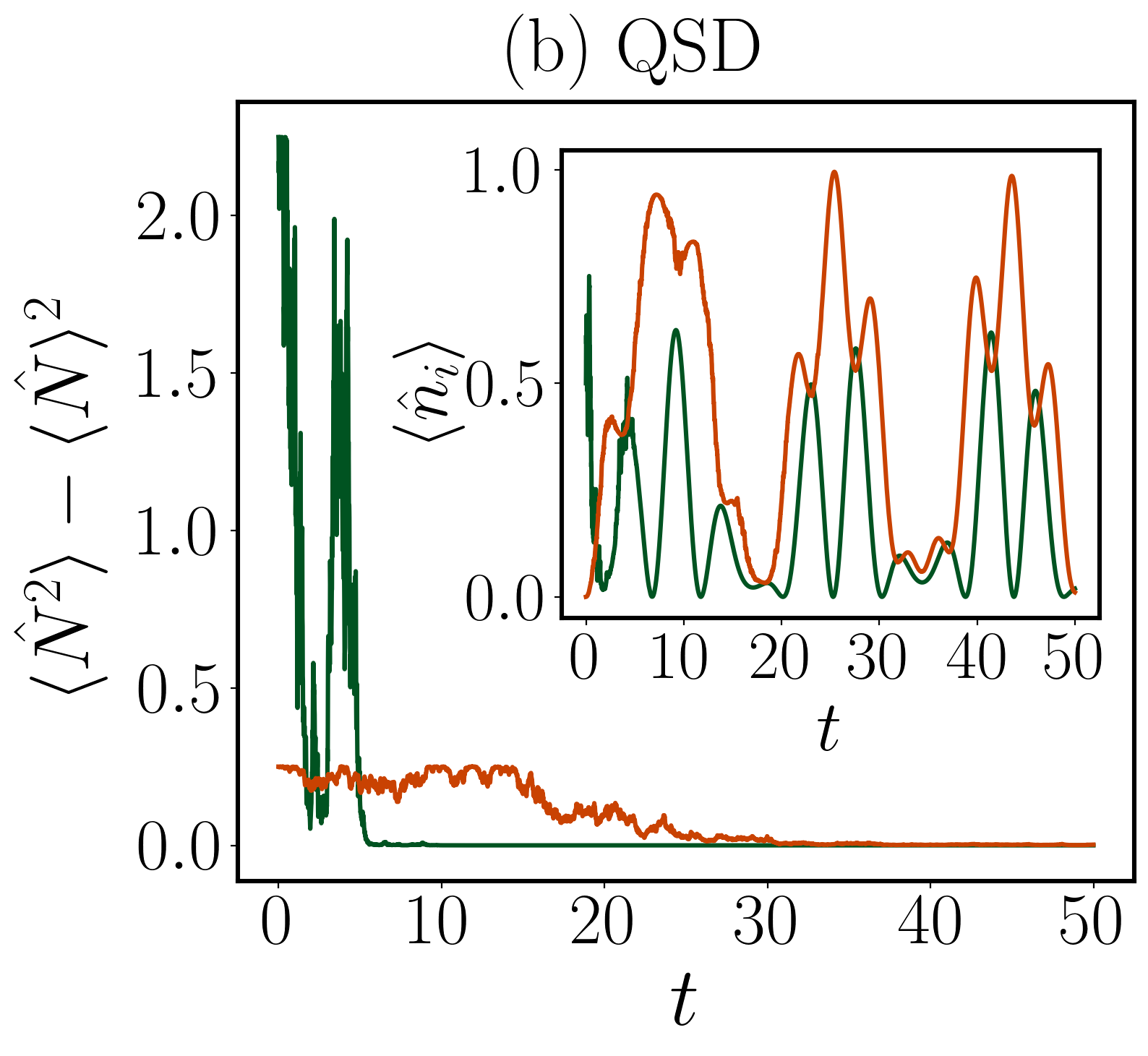
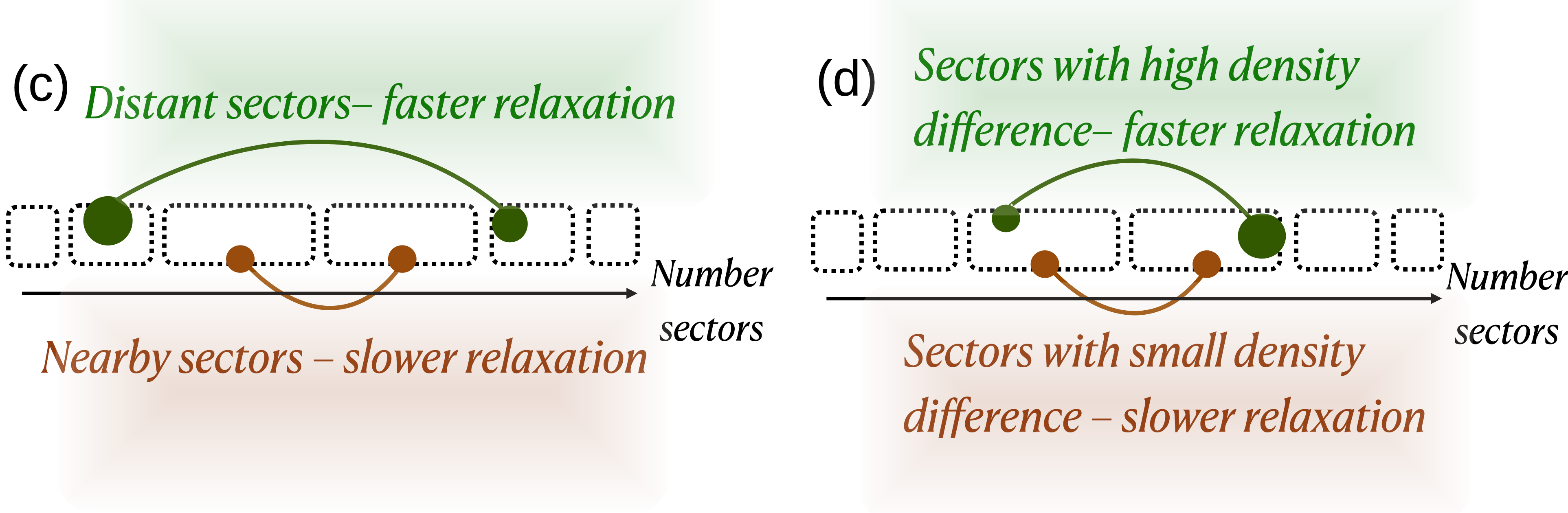
Symmetry restoration in quantum systems, observed as changes in the \DensityProfile, occurs as the system evolves over time. Our simulations demonstrate that the timescale for this restoration is inversely proportional to the separation between different number sectors of the system. Larger separations between these sectors-defined by the eigenvalues of the \NumberOperator-result in slower symmetry restoration, while smaller separations facilitate a more rapid return to a symmetric state. This relationship provides a quantitative measure for predicting the dynamics of symmetry recovery following a perturbation or symmetry-breaking event.
Accelerated Evolution: When Observation Reshapes the Quantum Timeline
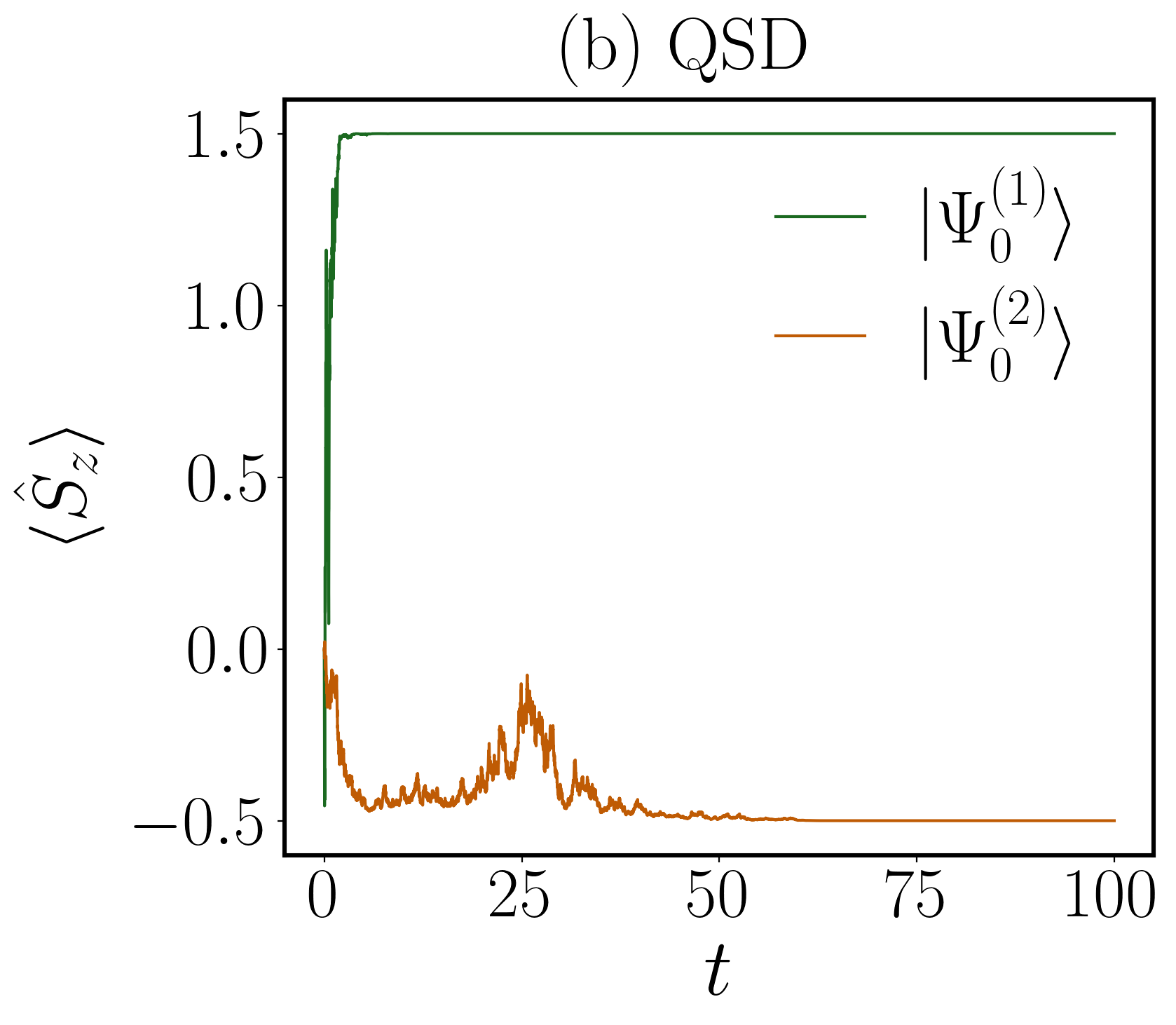
Systems subjected to continuous measurement exhibit a striking tendency to return to equilibrium at a significantly faster rate than their isolated counterparts. This phenomenon, termed ‘FasterRelaxation’, arises because the act of measurement effectively introduces a constant source of information about the system’s state, nudging it towards the most probable configuration. Unlike isolated systems which evolve according to their inherent dynamics, measured systems are continually ‘reset’ by the measurement process, suppressing fluctuations and accelerating the decay of initial conditions. The effect isn’t merely observational; the measurement actively participates in shaping the system’s evolution, acting as a persistent, albeit weak, driving force towards equilibrium. This is particularly pronounced when considering systems with internal symmetries, where measurement can selectively stabilize certain states and accelerate the restoration of those symmetries, fundamentally altering the relaxation pathway compared to a scenario devoid of external observation.
The rate at which a quantum system returns to equilibrium is deeply connected to both the act of measurement and the system’s initial condition, particularly concerning its symmetry. Research demonstrates that states initially far from equilibrium-those exhibiting a significant separation between what are known as ‘number sectors’-undergo faster symmetry restoration when subjected to continuous observation. This acceleration isn’t merely a consequence of measurement in general, but is linked to the system’s inherent structure; greater initial asymmetry implies a more pronounced drive toward restoring balance. Analysis of entropy asymmetry provides a quantifiable measure of this effect, revealing that the larger the initial separation between number sectors, the quicker the system reorganizes itself toward a symmetrical state, effectively expedited by the ongoing process of measurement.
The evolution of entanglement within a quantum system serves as a sensitive indicator of its journey towards, or deviation from, equilibrium. As a system undergoes dynamic processes – such as accelerated relaxation due to continuous measurement – shifts in its entanglement structure are often observed. These `EntanglementTransitions` aren’t merely passive consequences; they actively signal the non-equilibrium state, revealing how correlations between quantum constituents are being reshaped by external influences or internal dynamics. A sudden change in the degree or type of entanglement can therefore pinpoint moments of significant change, indicating that the system is not yet settled into a stable, predictable configuration. Analyzing these transitions offers valuable insight into the underlying mechanisms driving the system’s behavior and confirms its departure from a state of thermal equilibrium, where entanglement would typically reach a steady, minimal value.
The XX Hamiltonian serves as a crucial theoretical framework for investigating the interplay between measurement and accelerated relaxation dynamics. This model, which accounts for interactions and the magnetic moment within the system, demonstrates that the method of observation significantly impacts the rate of symmetry restoration. Investigations into initial states, such as |Φ₀(1)⟩, reveal a compelling phenomenon: local monitoring consistently accelerates the return to equilibrium faster than global monitoring techniques. This suggests that focusing measurements on specific, localized aspects of the system enhances the disruption of initial imbalances and facilitates a more rapid restoration of symmetry, offering insights into how observation itself can actively shape the evolution of quantum systems.
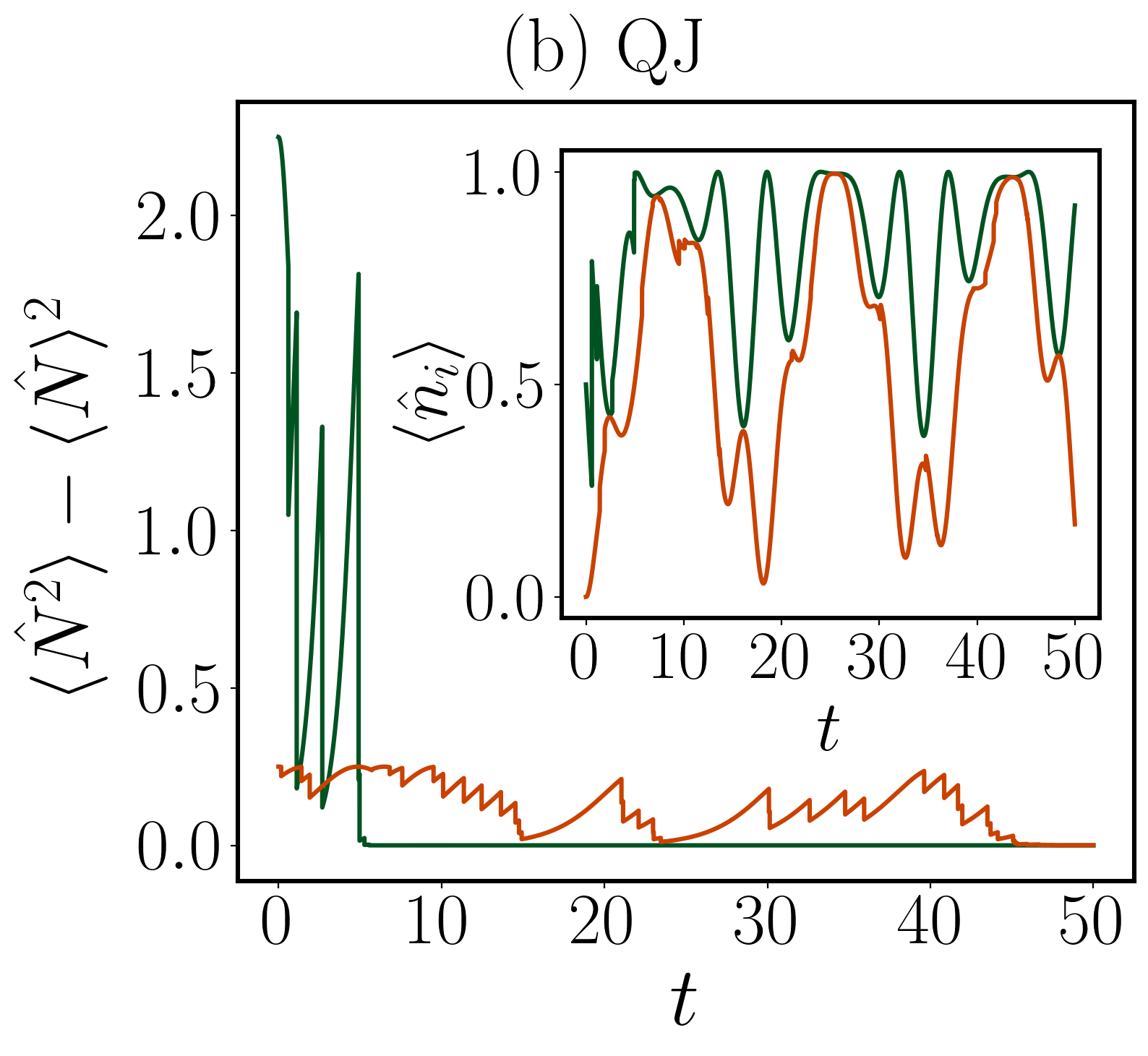
The research into quantum trajectories reveals a system eager to be prodded, its restoration of U(1) symmetry demonstrably influenced by the very act of observation. This echoes a fundamental principle articulated by Marcus Aurelius: “Everything we hear is an echo of an unspoken thought.” Just as the quantum system’s symmetry isn’t a fixed property but a response shaped by measurement backaction, so too are perceptions colored by internal states. The study highlights that localized measurements accelerate symmetry restoration, suggesting the system isn’t passively awaiting equilibrium but actively responding to stimuli-a dynamic interplay between observer and observed, mirroring the ceaseless internal dialogue shaping understanding.
Pushing the Boundaries
The observed acceleration of symmetry restoration via measurement in quantum trajectories isn’t merely a curious speed-up; it’s an invitation to disassemble established intuitions. If relaxation dynamics are so pliable under observation, what other ostensibly fundamental timescales are similarly contingent? The dependence on initial state-the faster decay of distant number sectors-hints at a hidden geometry within the Hilbert space, a landscape where the cost of restoration isn’t uniform. This suggests the possibility of engineering initial states specifically designed to exploit these vulnerabilities, effectively ‘pre-weakening’ the system for faster manipulation.
However, the current work primarily explores the ‘how’ of acceleration, leaving the ‘why’ largely untouched. Is the measurement backaction truly altering the underlying dynamics, or is it simply revealing a pre-existing, hidden relaxation pathway? Furthermore, the distinction between local and global measurements, while demonstrated, begs the question of optimal measurement strategies. A truly comprehensive understanding demands exploring measurement schemes that dynamically adapt based on the system’s evolving state-a feedback loop pushing the boundaries of quantum control.
Ultimately, this research isn’t a destination, but a provocation. If one can manipulate the very timescales governing quantum behavior, the implications extend far beyond relaxation dynamics. It forces a re-evaluation of the bedrock assumptions about predictability and control in open quantum systems-a necessary dismantling if one intends to truly understand, and ultimately engineer, reality.
Original article: https://arxiv.org/pdf/2601.18458.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Donkey Kong Country Returns HD version 1.1.0 update now available, adds Dixie Kong and Switch 2 enhancements
- Ashes of Creation Rogue Guide for Beginners
- Sega Insider Drops Tease of Next Sonic Game
- When to Expect One Piece Chapter 1172 Spoilers & Manga Leaks
- Fantasista Asuka launches February 12
- AAA Ubisoft Games Now $6 for Limited Time
- Best Werewolf Movies (October 2025)
- 10 Movies That Were Secretly Sequels
- All 6 Takopi’s Original Sin Episodes, Ranked
2026-01-28 01:22