Author: Denis Avetisyan
New research delves into the complex viscous properties of quark matter, revealing how its resistance to flow changes as it transitions between different states.
This study investigates the behavior of bulk and shear viscosity in quark matter using the PNJL model to characterize its response near the QCD phase transition and critical endpoint.
Understanding the transport properties of dense hadronic matter remains a significant challenge in high-energy physics, particularly concerning the viscous behavior near phase transitions. This work, ‘Bulk viscosity of quark matter across the QCD phase transitions’, investigates the temperature and density dependence of bulk and shear viscosities in quark matter utilizing a kinetic theory approach within the 2+1 flavor Polyakov-loop improved Nambu-Jona-Lasinio (PNJL) model. Calculations reveal a strong correlation between viscosity and the QCD phase structure, with enhanced values near chiral and first-order transitions and a surprising peak originating from the chiral crossover of strange quarks. How do these findings refine our understanding of hydrodynamic evolution in heavy-ion collisions and the properties of compact astrophysical objects?
The Echo of Creation: Unveiling the Primordial Fluid
The universe, moments after the Big Bang and recreated in modern experiments, briefly hosted a state of matter unlike any seen in everyday experience: the Quark-Gluon Plasma (QGP). Normally, quarks and gluons – the fundamental constituents of protons and neutrons – are confined within these particles by the strong force. However, when heavy ions, such as gold or lead nuclei, are collided at near-light speeds, the tremendous energy density overwhelms this confinement. This creates a fleeting, extraordinarily hot and dense environment where quarks and gluons become deconfined, existing as a plasma free to move independently. The resulting QGP is not simply a gas of free particles, but a complex, strongly interacting fluid, offering a unique window into the behavior of matter under extreme conditions and providing vital tests of the fundamental theory governing the strong force – Quantum Chromodynamics.
The creation of the Quark-Gluon Plasma (QGP) offers a unique window into the fundamental strong force, described by the theory of Quantum Chromodynamics (QCD). QCD predicts that at extremely high temperatures and densities, such as those created in heavy-ion collisions, matter undergoes a phase transition, liberating quarks and gluons from their confinement within hadrons. Precisely characterizing the QGP’s properties – its temperature, density, and viscosity – provides stringent tests of QCD’s predictions in a non-perturbative regime, where traditional calculations become exceedingly difficult. Discrepancies between experimental observations of the QGP and theoretical expectations derived from QCD would necessitate refinements to the theory, potentially revealing new physics beyond the Standard Model and deepening the understanding of how matter behaves at its most fundamental level. Therefore, investigations into the QGP are not merely about observing a new state of matter, but about validating – or challenging – the very foundations of the strong force.
Recent investigations into the Quark-Gluon Plasma (QGP) reveal a startling characteristic: it flows with remarkably little resistance, behaving as a nearly perfect fluid. Conventional theoretical models predicted a hot, dense plasma would exhibit high viscosity – essentially, internal friction – hindering its flow. However, experiments at facilities like the Relativistic Heavy Ion Collider and the Large Hadron Collider demonstrate the QGP possesses a shear viscosity to entropy density ratio incredibly close to the theoretical minimum, suggesting it flows more readily than any known substance. This unexpected fluidity challenges established understandings of strongly interacting matter and necessitates refinements to models describing the fundamental forces at play within the QGP, offering physicists a unique window into the nature of matter at extreme temperatures and densities.
Characterizing the quark-gluon plasma (QGP) demands precise measurement of its transport coefficients, notably shear and bulk viscosity, which dictate how the QGP flows and responds to stress. These coefficients aren’t merely descriptive; they are fundamentally linked to the QGP’s underlying properties, such as temperature and energy density, offering a window into the strong force described by Quantum Chromodynamics. Investigating these viscosities is exceptionally challenging because the QGP exists for only a fleeting moment, but scientists employ sophisticated techniques – analyzing the collective flow of particles created in heavy-ion collisions – to infer these crucial parameters. A surprisingly low shear viscosity, suggesting the QGP behaves as an almost ‘perfect fluid’, has been observed, prompting ongoing research to reconcile experimental findings with theoretical predictions and deepen understanding of matter under extreme conditions.
Modeling the Primordial Flow: Hydrodynamics and Transport
Hydrodynamic models are successfully employed to describe the collective behavior of the Quark-Gluon Plasma (QGP) created in heavy-ion collisions. These models treat the QGP as a fluid and utilize transport coefficients – parameters quantifying a fluid’s response to external stimuli – to characterize its flow properties. Key transport coefficients include shear viscosity η, bulk viscosity ζ, and thermal conductivity κ. The equations of motion for this fluid, incorporating these coefficients, predict features of the observed QGP evolution, such as anisotropic flow and momentum distributions. The ability of hydrodynamic simulations to reproduce experimental data strongly suggests that the QGP behaves, at least to a good approximation, as a strongly coupled fluid rather than a weakly interacting gas.
Determining the transport coefficients of the Quark-Gluon Plasma (QGP), specifically shear η and bulk ζ viscosity, presents a significant theoretical obstacle due to the strongly interacting nature of the medium. These coefficients are not simply material properties but are temperature and density dependent, requiring calculations based on the underlying dynamics of quark and gluon interactions. Direct experimental measurement is also challenging, necessitating reliance on theoretical modeling and comparisons to hydrodynamic simulations. The complexity arises from the need to bridge the gap between microscopic collision dynamics and macroscopic fluid behavior, demanding sophisticated many-body calculations and approximations to accurately predict the QGP’s response to external stimuli and its internal flow characteristics. Furthermore, accurately calculating these coefficients requires precise knowledge of the equation of state and the interplay between various degrees of freedom within the QGP.
Kinetic theory establishes a formal link between the microscopic dynamics of particle interactions within the Quark-Gluon Plasma (QGP) and its macroscopic transport properties, such as viscosity and thermal conductivity. This is achieved by statistically averaging over the distribution functions of the constituent particles, allowing transport coefficients to be expressed in terms of scattering cross sections – a measure of the probability of particle interactions. Specifically, the Boltzmann equation, a central tenet of kinetic theory, provides a framework for calculating these coefficients by relating them to the collision integral, which directly incorporates the scattering cross sections and particle velocities. Therefore, accurate knowledge of the microscopic interactions, quantified through these cross sections, is essential for predicting the macroscopic behavior of the QGP as described by hydrodynamic models.
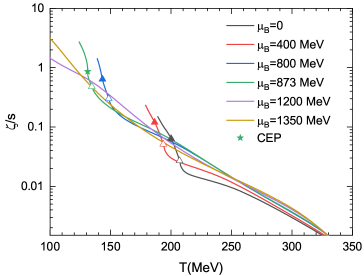
The Polyakov-Nambu-Jona-Lasinio (PNJL) model, when integrated within a Kinetic Theory approach, provides a means to estimate the masses and interaction strengths of quarks, parameters essential for calculating transport coefficients like viscosity. Recent research utilizing this framework indicates that the ratio of bulk viscosity ζ to shear viscosity η, expressed as the specific bulk viscosity \zeta/s , approaches zero at increasingly high temperatures. This finding is significant because it aligns with predictions from conformal field theory, which posits a near-zero bulk viscosity in the limit of a strongly coupled, nearly perfect fluid – a description increasingly considered applicable to the Quark-Gluon Plasma (QGP).
The Resistance to Compression: Bulk Viscosity and the Phase Transition
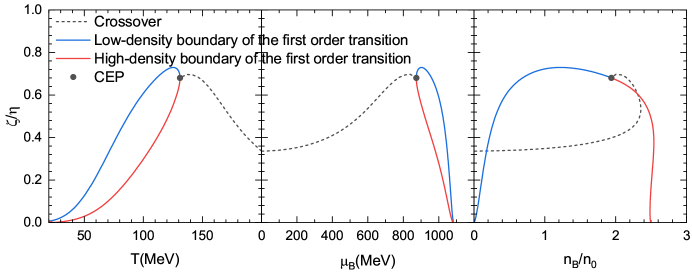
Bulk viscosity, denoted as ζ, quantifies a fluid’s resistance to compression or expansion under stress and is a critical parameter in modeling the Quark-Gluon Plasma (QGP). Within the QGP, fluctuations in energy density and pressure are substantial, and bulk viscosity governs the rate at which these fluctuations are damped or amplified. The QCD Phase Transition, representing the transition between hadronic matter and the QGP, significantly alters the thermodynamic properties of the system, directly influencing ζ. Specifically, changes in the equation of state and energy density during the phase transition contribute to a non-negligible bulk viscous pressure, impacting the QGP’s hydrodynamic evolution and collective flow characteristics. Therefore, accurately characterizing bulk viscosity is essential for understanding the QGP’s dynamic behavior and for interpreting experimental observations from heavy-ion collisions.
The Quark-Gluon Plasma (QGP)’s entropy density is directly modulated by the nature of the QCD Phase Transition. Different transition forms – including the Chiral Crossover and the Pion Mott Transition – result in varying degrees of entropy production and distribution within the QGP. As bulk viscosity ζ is fundamentally linked to the system’s ability to resist compression and is dependent on the energy density and pressure, changes in entropy density caused by the QCD Phase Transition directly influence the magnitude of ζ. Specifically, an increase in entropy density generally correlates with a higher bulk viscosity, and the specific type of transition dictates the magnitude and temperature dependence of this effect.
The trace anomaly, quantified as \theta(T) = \frac{1}{T} \in t d^4k \frac{k^2}{k^2 + m^2} f(k,T) , represents a deviation from the expected behavior of a conformal field theory and arises due to the mass scale introduced by Quantum Chromodynamics (QCD). This anomaly directly influences the bulk viscosity ζ through its contribution to the pressure tensor, altering the fluid’s resistance to compression or expansion. Specifically, the temperature dependence of the bulk viscosity is linked to the temperature dependence of the trace anomaly; as temperature decreases towards the QCD phase transition, the trace anomaly becomes larger and negative, increasing the magnitude of ζ. This connection implies that the bulk viscosity is not merely a constant but a dynamic property strongly correlated with the thermal state of the Quark-Gluon Plasma (QGP) and the underlying QCD dynamics.
Studies of the quark-gluon plasma (QGP) indicate that the ratio of bulk to shear viscosity \zeta/\eta exhibits a non-monotonic temperature dependence. Specifically, this ratio reaches maximum values in the vicinity of the chiral phase transition, surpassing those observed at the transition boundary for up, down, and strange quarks. However, as the temperature decreases and the system moves toward lower energy densities, \zeta/\eta rapidly diminishes, approaching a value of zero at extremely low temperatures. This behavior suggests a strong coupling between the QGP’s resistance to compression and the underlying chiral symmetry restoration or breaking mechanisms, with bulk viscosity becoming negligible in fully deconfined, low-temperature regimes.
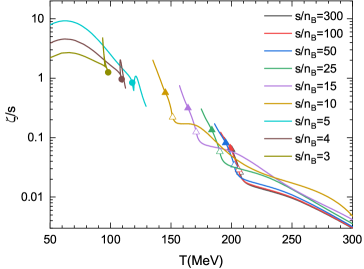
The Search for Stability: Mapping the Phase Diagram and the Critical Point
The search for the QCD Critical Endpoint continues with the Beam Energy Scan Phase II at the Relativistic Heavy Ion Collider (RHIC)-STAR. This experiment systematically varies the collision energy of heavy ions-gold nuclei, specifically-to map out the region of the QCD phase diagram where ordinary matter transitions to the Quark-Gluon Plasma (QGP). By meticulously analyzing the collision products at different energies, researchers seek evidence of dramatic changes in particle production-signatures indicating the proximity to the Critical Endpoint. This endpoint represents a point of inflection in the phase transition between hadronic matter and the QGP, potentially shifting from a smooth crossover to a first-order phase transition. Precisely locating this endpoint is vital, as it will refine understanding of the strong nuclear force and the properties of matter under extreme temperatures and densities, mirroring conditions shortly after the Big Bang.
Precisely locating the Critical Endpoint and characterizing the nature of the quark-gluon plasma (QGP) phase transition are fundamental to fully understanding the QGP’s properties. The transition from hadronic matter to the QGP isn’t simply a shift between states; it could be a smooth crossover, a first-order phase transition with a distinct boundary, or something more complex. Classifying this transition using the Halperin-Hohenberg scheme – which defines universality classes based on the symmetry breaking patterns and critical exponents – allows physicists to predict the QGP’s behavior near the critical point. Determining the correct universality class has profound implications for understanding the QGP’s transport coefficients, such as viscosity and thermal conductivity, and ultimately, the early universe’s evolution – because the conditions present shortly after the Big Bang are thought to have created a similar state of matter. A clear classification allows for precise theoretical predictions that can be rigorously tested against experimental data, driving a deeper comprehension of this exotic state of matter.
The evolution of the Quark-Gluon Plasma (QGP), a state of matter existing at extraordinarily high temperatures, isn’t random; it follows predictable pathways dictated by the principle of constant entropy, visualized as isentropic trajectories. These trajectories represent paths in a multi-dimensional space of thermodynamic variables – temperature, pressure, energy density, and baryon chemical potential – where entropy remains unchanged. By mapping the QGP’s journey along these constant-entropy lines, physicists gain crucial insights into its behavior and can connect initial conditions of the collision to the final observed state. Understanding these trajectories is vital because the QGP isn’t simply cooling; it’s transitioning through different phases, and the precise path it takes is sensitive to the location of the critical endpoint and the nature of the phase transition, allowing researchers to test theoretical models and refine their understanding of strong interactions. S = const is the fundamental principle guiding this analysis, turning the complex evolution of the QGP into a more manageable and interpretable process.
The Kovtun-Son-Starinets (KSS) lower bound represents a significant theoretical constraint in the study of the quark-gluon plasma (QGP). This bound, derived from hydrodynamic principles and incorporating the concept of causality, posits a minimum value for the ratio of shear viscosity η to entropy density s ; specifically, \frac{\eta}{s} \geq \frac{1}{4\pi} . Researchers utilize this benchmark to evaluate the validity of various theoretical models attempting to describe the QGP’s behavior, comparing predicted values of \eta / s against this established lower limit. Experimental data, particularly from heavy-ion collision experiments at facilities like RHIC and the LHC, strives to constrain the value of this ratio, with current findings suggesting the QGP is a nearly perfect fluid, exhibiting viscosities remarkably close to this theoretical minimum. This comparison between theory and experiment not only validates hydrodynamic approaches to understanding the QGP but also provides insight into the fundamental properties of strongly coupled matter.
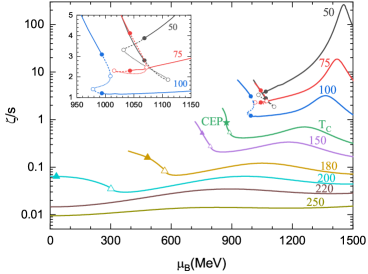
The study of quark matter’s viscosities reveals a system acutely sensitive to its internal state, much like any complex structure experiencing transition. This sensitivity to phase changes-the shift between hadronic matter and the Quark-Gluon Plasma-echoes a fundamental principle of existence. As John Dewey observed, “Education is not preparation for life; education is life itself.” Similarly, the evolution of quark matter, as modeled by the PNJL model, isn’t merely a prelude to a final state; the viscous behaviors are the manifestation of the system’s ongoing adaptation and response to changing conditions. The distinct behaviors near the critical endpoint highlight how systems reveal their truest nature during moments of transformation.
What Lies Ahead?
The investigation into transport coefficients, specifically bulk and shear viscosity within quark matter, reveals less a definitive answer and more a refinement of the questions. The PNJL model, while a useful construct, remains an approximation – a snapshot of a flowing system. Uptime is merely temporary; the model’s limitations become increasingly apparent when probing the nuances of the QCD phase structure. The sensitivity of these viscosities to the phase transition is not surprising; all boundaries introduce impedance. What remains is the challenge of mapping this impedance across the entire phase diagram, acknowledging that any such map is necessarily incomplete.
The search for the critical endpoint, and the associated non-equilibrium dynamics, demands a move beyond static calculations. Stability is an illusion cached by time. Future efforts must address the time-dependent behavior of these transport coefficients, exploring how they evolve as the system traverses the phase boundary. Hydrodynamic simulations, informed by more realistic equations of state, will be crucial. Yet even these simulations will only approximate the truth – a complete understanding remains asymptotic.
Ultimately, the study of quark matter is an exercise in acknowledging inherent limitations. Latency is the tax every request must pay. Each calculation, each simulation, introduces a delay, a distortion of the underlying reality. The goal is not to eliminate this latency, but to understand its origins and minimize its impact, accepting that a perfectly accurate depiction of this complex system is, and will remain, beyond reach.
Original article: https://arxiv.org/pdf/2601.10126.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Darkwood Trunk Location in Hytale
- How To Watch A Knight Of The Seven Kingdoms Online And Stream The Game Of Thrones Spinoff From Anywhere
- Best Controller Settings for ARC Raiders
- Hytale: Upgrade All Workbenches to Max Level, Materials Guide
- Ashes of Creation Rogue Guide for Beginners
- Olympian Katie Ledecky Details Her Gold Medal-Winning Training Regimen
- Daredevil Is Entering a New Era With a Chilling New Villain (And We Have A First Look) (Exclusive)
- RHOBH’s Jennifer Tilly Reacts to Sutton Stracke “Snapping” at Her
- Francia Raisa Reacts to Selena Gomez’s Wedding to Benny Blanco
- The Rip Ending Explained: Who’s The Traitor (And What Those Tattoos Are About) In Ben Affleck And Matt Damon Thriller
2026-01-19 05:00