Quarkonium in Motion: How Magnetic Fields Drive State Transitions

by

Author: Denis Avetisyan

New research details the dynamic behavior of quarkonium states as they respond to changing magnetic fields, revealing the crucial role of sweep rate and field shape.

The study demonstrates that a triangular magnetic-field pulse induces measurable Stückelberg oscillations-interference between amplitudes from two avoided crossings in the adiabatic energies <span class="katex-eq" data-katex-display="false">E_{\pm}(t)</span>-resulting in a final transition probability that aligns with predictions from the Landau-Zener-Stückelberg (LZS) theory as a function of pulse duration <span class="katex-eq" data-katex-display="false">t_{max}</span>.
The study demonstrates that a triangular magnetic-field pulse induces measurable Stückelberg oscillations-interference between amplitudes from two avoided crossings in the adiabatic energies E_{\pm}(t)-resulting in a final transition probability that aligns with predictions from the Landau-Zener-Stückelberg (LZS) theory as a function of pulse duration t_{max}.

This study employs multi-channel Landau-Zener Hamiltonians to investigate nonadiabatic transitions and Stückelberg interference in magnetized charmonium systems.

The behavior of hadrons in strong magnetic fields remains incompletely understood, particularly concerning the dynamics at avoided level crossings. This work, ‘Landau-Zener-Stückelberg-Majorana dynamics of magnetized quarkonia,’ investigates these nonadiabatic transitions in charmonium by employing a multi-channel Landau-Zener Hamiltonian to model the system’s evolution under time-dependent magnetic fields. Our analysis reveals that the sweep rate and field profile significantly influence occupation probabilities, exhibiting both Landau-Zener transitions and Stückelberg interference effects. How do these findings inform our understanding of the real-time evolution of magnetized strongly-interacting matter and potentially guide future lattice QCD simulations?

Unveiling Charmonium: A Window into the Strong Force

Charmonium, a composite particle consisting of a charm quark and its antiquark counterpart, offers physicists a unique window into the realm of quantum chromodynamics (QCD), the theory governing the strong nuclear force. Because charmonium is not subject to the same complexities as hadrons containing lighter quarks, it provides a relatively clean system for testing QCD predictions. The energy levels and decay patterns of charmonium are exquisitely sensitive to the details of the strong interaction, allowing researchers to map the underlying forces with unprecedented precision. By meticulously studying its properties-including its mass spectrum and transition rates-scientists can validate theoretical models and refine O(α_s) calculations, ultimately deepening understanding of how quarks and gluons bind together to form matter.

Charmonium, a composite particle consisting of a charm quark and its antiquark counterpart, presents a unique opportunity to rigorously test the predictions of quantum chromodynamics (QCD), the theory describing the strong nuclear force. By subjecting charmonium to precisely controlled external magnetic fields, physicists can probe the intricate interplay between its internal structure and the fundamental forces governing quark interactions. Deviations from theoretical predictions, observed through the analysis of charmonium’s response to these fields, would signal the need for refinements to QCD or potentially hint at new physics beyond the Standard Model. This sensitivity arises because the strong force, unlike electromagnetism, does not diminish with distance, making charmonium an ideal system for exploring the non-perturbative regime of QCD where calculations are exceptionally challenging and experimental validation is paramount.

Investigations into charmonium – a bound state of charm and anticharm quarks – utilize time-dependent magnetic fields to induce transitions between its distinct energy levels. These transitions aren’t simple jumps, but rather complex dynamics accurately modeled by multi-channel Landau-Zener Hamiltonians. This framework accounts for the coupling between different quantum states as the magnetic field changes, allowing physicists to predict the probability of transitioning from one energy level to another. Crucially, the Landau-Zener Hamiltonian provides a means to study non-adiabatic transitions, where the system doesn’t remain in its initial state throughout the field change, offering a powerful tool to map the energy landscape of charmonium and test the predictions of quantum chromodynamics. The precision of these calculations enables detailed comparisons with experimental data, refining understanding of strong interactions at a fundamental level.

The multi-channel LZ Hamiltonian, fitted to the quark-model spectrum and detailed in Table 1, accurately reproduces both low-lying and higher excited states-including additional avoided crossings-as the number of channels increases.
The multi-channel LZ Hamiltonian, fitted to the quark-model spectrum and detailed in Table 1, accurately reproduces both low-lying and higher excited states-including additional avoided crossings-as the number of channels increases.

The Landau-Zener Framework: A Mechanism for Transition

The Landau-Zener transition describes the probability of a quantum system transitioning between two adiabatic energy eigenstates when subjected to a time-dependent perturbation. This non-adiabatic process occurs when the instantaneous energy gap between the states closes, and the system cannot remain in the initial state due to the rate of change of the perturbation. Unlike adiabatic processes where the system remains in the instantaneous ground state, the Landau-Zener transition predicts a finite probability of transitioning to the excited state, dependent on factors such as the energy gap size and the rate of change of the external field. This mechanism is crucial for understanding phenomena in diverse physical systems, including molecular spectroscopy, quantum computing, and condensed matter physics, where external fields or other time-dependent influences drive transitions between quantum states.

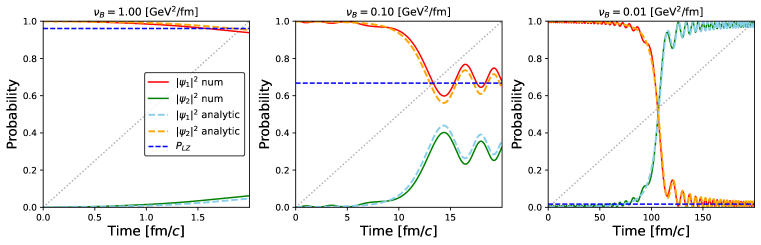
The probability of a Landau-Zener transition is acutely dependent on both the rate of change of the external field, denoted as ν_{eff}, and the magnitude of the energy gap, Δ, between the initial and final quantum states. Experimental observation of this sensitivity involves systematically varying the sweep rate while monitoring transition probabilities; slower sweep rates generally favor adiabatic passage and suppressed transitions, whereas faster rates promote non-adiabatic transitions. Furthermore, specific sweep rates can induce coherent oscillations in the transition probability as the system repeatedly traverses the avoided crossing, demonstrating a clear relationship between the rate, energy gap, and the resulting transition dynamics. The parameter λ = Δ²/|ν_{eff}| encapsulates this dependence, with larger values indicating a higher probability of remaining in the initial state during the sweep.

The Landau-Zener model relies on a time-dependent Hamiltonian to describe the system’s evolution, typically expressed with a two-level structure and a coupling term representing the interaction between states. A crucial parameter in determining the probability of non-adiabatic transitions is λ = \frac{\Delta^2}{|\nu_{eff}|}, where Δ represents the energy gap between the two levels and ν_{eff} is the effective sweep rate of the external field. A small value of λ indicates a high probability of transition, meaning the system is more likely to undergo a non-adiabatic transition, while a large value suggests adiabatic behavior. The accurate construction of this Hamiltonian and the precise determination of these parameters are essential for quantitatively predicting the transition probability and understanding the system’s response to external perturbations.

Numerical solutions of the time-dependent Schrödinger equation closely match the analytic Landau-Zener prediction-marked by the blue dashed line-despite a difference in initial conditions that prevents the analytic solution from capturing pre-crossing oscillations.
Numerical solutions of the time-dependent Schrödinger equation closely match the analytic Landau-Zener prediction-marked by the blue dashed line-despite a difference in initial conditions that prevents the analytic solution from capturing pre-crossing oscillations.

Beyond Simple Transitions: The Role of Interference

Avoided crossings occur in systems where two or more energy eigenstates become degenerate, but are prevented from actually crossing due to non-zero coupling between the states. This coupling introduces a repulsive force, creating a gap in the potential energy surface and altering the energy level trajectories. The magnitude of this gap is directly proportional to the strength of the coupling; stronger coupling results in a larger avoided crossing region. These features are critical because they significantly modify the system’s dynamics near the avoided crossing, influencing transition probabilities and requiring consideration beyond simple diabatic approximations. The potential energy surface, therefore, is not characterized by true intersections but rather by these repulsive interactions which dictate the system’s evolution.

Stückelberg interference arises from the coherent superposition of different pathways a system can take during a rapid passage through an avoided crossing. The standard Landau-Zener (LZ) formula calculates transition probabilities based on a single pathway, assuming only one possible route for the system to evolve. However, when an avoided crossing is present, the wavefunction splits and evolves along both the upper and lower branches before recombining. This interference between these pathways leads to oscillations in the transition probability as a function of parameters like pulse duration or the velocity of the system. Consequently, the actual transition probability deviates from the prediction of the LZ formula, exhibiting enhancements or suppressions dependent on the phase accumulated along each path; the overall effect is a modification of the transition probability that must be accounted for to accurately describe the system’s dynamics.

Combining Landau-Zener and Stückelberg interference effects provides a more complete model of non-adiabatic transitions than either approach alone. The standard Landau-Zener formula calculates transition probabilities based on the velocity and coupling strength at the avoided crossing; however, it neglects the oscillatory interference arising from multiple reflections between the potential energy surfaces. This interference, quantified by the Stückelberg effect, becomes significant when the pulse duration is comparable to the time it takes to traverse the avoided crossing region. Accurately accounting for both effects allows for precise modeling of transition probabilities as a function of pulse duration, which is critical for controlling the system’s dynamics and predicting experimental outcomes. Specifically, the sensitivity of transition probabilities to pulse duration is enhanced by the interplay between the Landau-Zener tunneling and the Stückelberg oscillations.

Diabatic probabilities <span class="katex-eq" data-katex-display="false">P_{\rm dia}[J/\psi]</span> reveal Stückelberg interference and sensitivity to the parameter <span class="katex-eq" data-katex-display="false">\gamma_{P}[fm/cc]</span> in a two-channel model initialized with <span class="katex-eq" data-katex-display="false">\psi=(1,0)^{T}</span>.
Diabatic probabilities P_{\rm dia}[J/\psi] reveal Stückelberg interference and sensitivity to the parameter \gamma_{P}[fm/cc] in a two-channel model initialized with \psi=(1,0)^{T}.

Shaping the Quantum Landscape: Field Profiles and System Response

The manipulation of quantum states relies heavily on precisely tailored time-dependent magnetic fields, with researchers employing a diverse range of profiles to induce transitions between energy levels. These fields aren’t simply switched on or off; instead, profiles like linear ramps – providing a consistent rate of change – are contrasted with the sharper, more localized effects of Gaussian pulses. Furthermore, exponential decays offer a unique dynamic, mimicking natural relaxation processes and enabling investigations into transient quantum phenomena. The specific shape of the applied field dramatically alters the probability of these transitions, influencing the final quantum state achieved and providing a powerful tool for controlling and exploring the intricacies of quantum systems – a capability vital for advancements in quantum computing and materials science.

The manner in which an external magnetic field changes over time demonstrably influences the likelihood of quantum transitions and the ultimate state the system settles into. A slowly varying field, for instance, favors adiabatic transitions – a smooth evolution where the system remains in its instantaneous eigenstate – while a rapid, abrupt change promotes non-adiabatic transitions, potentially exciting the system to higher energy levels or inducing interlevel crossings. This sensitivity stems from the time-dependent Schrödinger equation, where the rate of change in the Hamiltonian – dictated by the field profile – directly affects the transition probability amplitudes. Consequently, tailoring the field’s temporal shape – whether employing a linear ramp, a \text{sech}^2 pulse, or an exponential decay – becomes a powerful tool for steering the system’s quantum evolution and selectively populating desired states, impacting phenomena like Landau-Zener tunneling and Rabi oscillations.

The ability to correlate specific time-dependent magnetic field profiles with resulting quantum state transitions unlocks a pathway to manipulate a system’s evolution with remarkable precision. Researchers find that by carefully tailoring these fields-whether employing linear ramps, Gaussian pulses, or exponential decays-they can not only steer the system towards desired quantum states, but also thoroughly investigate its inherent properties. This level of control is further substantiated by the successful application of multi-channel Landau-Zener Hamiltonians, which accurately model the observed dynamics and provide a theoretical framework for predicting and optimizing transitions. Consequently, these investigations not only deepen the understanding of quantum phenomena but also lay the groundwork for advanced quantum technologies reliant on precise state control and manipulation.

The two-channel model demonstrates avoided crossings driven by linear ramps, Gaussian decays, and Gaussian pulses-representing single and double passages-with arrows indicating the direction of time evolution along the magnetic-field trajectories.
The two-channel model demonstrates avoided crossings driven by linear ramps, Gaussian decays, and Gaussian pulses-representing single and double passages-with arrows indicating the direction of time evolution along the magnetic-field trajectories.

The study meticulously details the dynamics of quarkonia under fluctuating magnetic fields, revealing a complexity that echoes a broader principle of scientific inquiry. As Paul Feyerabend observed, “Anything goes.” This isn’t a call for chaos, but rather an acknowledgement that rigid adherence to a single methodology can stifle understanding. The researchers’ approach – constructing multi-channel Landau-Zener Hamiltonians to model nonadiabatic transitions – demonstrates a willingness to employ diverse theoretical tools to navigate the intricacies of the system. The sensitivity of occupation probabilities to sweep rate, as highlighted in the article, reinforces the idea that observation itself is an intervention, and the ‘rules’ governing these transitions are context-dependent. This flexibility is not a weakness, but a testament to the power of adaptable thinking in unraveling complex phenomena.

Beyond the Sweep

The treatment of magnetized quarkonia, while elegantly framed within a multi-channel Landau-Zener formalism, inevitably highlights the limitations inherent in simplifying complex quantum systems. Each parameter chosen-the precise form of the magnetic field, the discretization of the continuum, the selection of initial states-represents a tacit acknowledgement of unmodeled physics. Future iterations must address the sensitivity of these results to such choices, perhaps through a systematic exploration of parameter space or the development of more robust, field-free benchmarks.

A particularly intriguing, yet largely untouched, area concerns the interplay between Stückelberg interference and decoherence. The presented framework meticulously calculates interference probabilities, but the realistic environment within a quark-gluon plasma – or even within a heavy-ion collision – will introduce decoherence mechanisms that erode these delicate effects. The question isn’t simply whether interference can occur, but whether it is observable, and what information it might reveal amidst the noise.

Ultimately, the pursuit of a truly predictive theory demands a move beyond the adiabatic approximation. While the Landau-Zener framework offers valuable insight, it is, by its very nature, a description of transitions between states. A more complete picture requires a fully time-dependent solution of the Schrödinger equation, a computationally demanding task, but one that might reveal subtle, yet crucial, features of quarkonium dynamics currently obscured by the approximations employed.

Original article: https://arxiv.org/pdf/2512.24072.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-01-03 12:21