Relaxing Gravity: How String Theory Fields Could Break the Rules

Author: Denis Avetisyan

New research uses dynamical systems to explore how the evolution of a fundamental field in string theory impacts the equivalence principle-a cornerstone of general relativity.

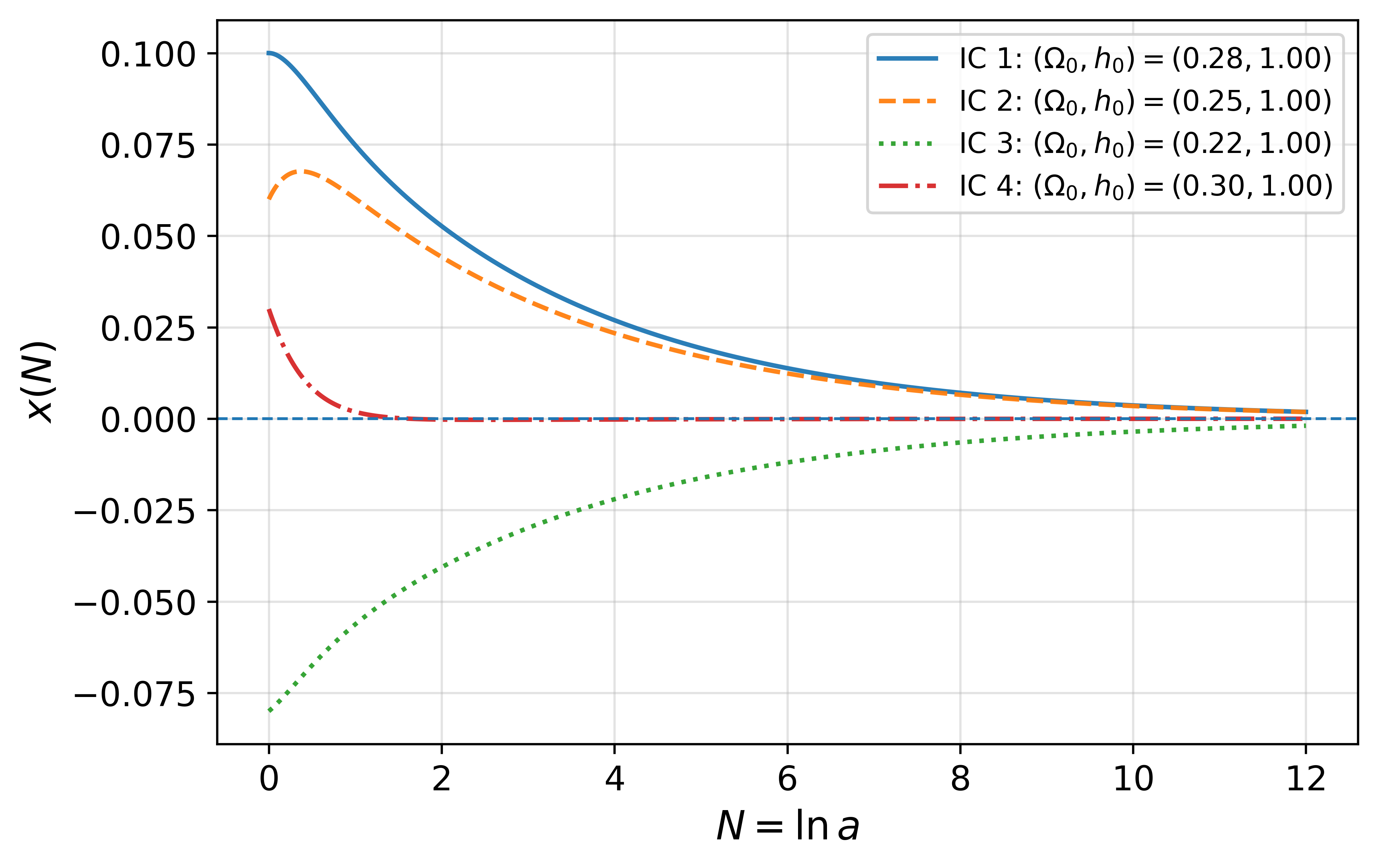
The evolution of a dimensionless scalar displacement, <span class="katex-eq" data-katex-display="false">\frac{\phi-\phi_{\ast}}{M_{\rm Pl}}</span>, consistently dampens and relaxes towards zero as expressed by <span class="katex-eq" data-katex-display="false">N = \ln a</span>, indicating a progressive suppression of composition-dependent fifth forces and deviations from the equivalence principle within the Damour-Polyakov regime, where ambient matter coupling scales proportionally to this displacement. — The evolution of a dimensionless scalar displacement, $\frac{\phi-\phi_{\ast}}{M_{\rm Pl}}$ , consistently dampens and relaxes towards zero as expressed by $N = \ln a$ , indicating a progressive suppression of composition-dependent fifth forces and deviations from the equivalence principle within the Damour-Polyakov regime, where ambient matter coupling scales proportionally to this displacement.

This paper develops a dynamical systems framework to demonstrate how the cosmological relaxation of a dilaton field in string theory controls deviations from the equivalence principle, linking it to potentially measurable effects in gravity.

The equivalence principle, a cornerstone of general relativity, faces subtle challenges in modified gravity theories predicting scalar-tensor interactions. This is explored in ‘A dynamical systems approach to studying the equivalence principle in dilaton gravity’, which utilizes dynamical systems methods to investigate cosmological relaxation and its impact on deviations from this principle. By analyzing a string-inspired dilaton cosmology within the Damour-Polyakov regime, we demonstrate that the late-time evolution of the dilaton field directly controls the magnitude of fifth-force effects and thus measurable violations of the equivalence principle. Can these phase-space techniques offer a robust framework for connecting cosmological dynamics to precision tests of gravity and ultimately constrain fundamental parameters of modified gravity theories?

The Universe’s Hidden Dial: Introducing the Dilaton

Theoretical frameworks beyond established particle physics, most notably string theory, posit the existence of scalar fields that permeate the universe – among these, the dilaton stands out as a particularly intriguing possibility. Unlike force-carrying particles like photons or gluons, scalar fields possess a value at every point in space, and the dilaton is hypothesized to interact with all other matter and energy. Crucially, this interaction isn’t through the traditional forces, but via a modification of spacetime itself – a conformal rescaling that subtly alters distances and timescales. The implications are profound, potentially uniting gravity with the other fundamental forces by providing a dynamic component to the gravitational constant and offering a pathway to explore quantum gravity. While yet unobserved, the dilaton represents a compelling theoretical link between the seemingly disparate realms of particle physics and cosmology, prompting ongoing research into its possible detection and role in the universe’s evolution.

The concept of a dilaton field offers a compelling pathway to investigate potential refinements to Einstein’s theory of general relativity. This scalar field doesn’t directly gravitate in the traditional sense, but instead interacts with all matter and energy through a process called conformal rescaling – effectively altering the size and shape of spacetime without changing angles. This unique coupling allows physicists to explore scenarios where gravity isn’t solely described by the curvature of spacetime, as in general relativity, but is modulated by the dilaton’s value at each point in space and time. Consequently, the dilaton provides a theoretical framework for examining alternative gravitational models and testing the limits of our current understanding, potentially revealing new physics at extreme energy scales or in the early universe. By manipulating the dilaton field within theoretical models, researchers can investigate how fundamental constants might vary and explore the implications for cosmology and particle physics.

The intricate coupling between the dilaton field and matter doesn’t simply refine general relativity; it challenges a foundational tenet of gravitational physics – the Equivalence Principle. This principle, asserting the universality of free fall regardless of an object’s composition, underpins much of modern physics. However, the dilaton’s influence introduces a dependence on the specific properties of matter. Different materials will effectively experience slightly altered gravitational interactions due to their varying couplings to the dilaton field, potentially leading to measurable deviations in their free-fall rates. While experimental tests have, thus far, strongly upheld the Equivalence Principle, the dilaton framework provides a theoretical avenue for its subtle violation, demanding ever-more-precise experiments to probe the boundaries of this fundamental law and potentially reveal new physics beyond Einstein’s theory.

Mapping the Cosmos: The FLRW Framework

Dynamical systems methods are utilized to investigate the temporal evolution of the dilaton field within the context of a spatially flat Friedmann-Lemaître-Robertson-Walker (FLRW) universe. This approach involves representing the dilaton field’s behavior as a system of first-order differential equations, allowing for the analysis of its phase space and the identification of fixed points and attractors. The FLRW metric, defined as $ds^2 = -dt^2 + a^2(t) \delta_{ij} dx^i dx^j$ , provides the background spacetime within which the dilaton evolves, and the dynamical systems framework enables a systematic exploration of solutions to the governing equations that describe the dilaton’s influence on cosmological expansion.

The Friedmann-Lemaître-Robertson-Walker (FLRW) framework facilitates the analysis of cosmological solutions by representing their evolution within a phase space. This phase space is constructed using relevant dynamical variables, allowing for a geometric visualization of possible universe trajectories. By mapping the behavior of the dilaton field – a scalar field influencing gravitational interactions – within this space, we can determine its relationship to the cosmic scale factor, which dictates the universe’s expansion rate. Specific trajectories and fixed points in the phase space correspond to different cosmological scenarios, and their stability reveals whether the universe will expand, contract, or remain static. The dilaton’s interaction with the expansion is thus quantified by observing its movement and evolution within this phase-space structure, providing insights into the dynamics of the universe and the nature of gravity.

The evolution of the dilaton field is governed by the Scalar Equation, a second-order differential equation determining its temporal behavior within the FLRW metric. Analysis of this equation reveals a suppression of deviations from the equivalence principle as the scalar field displacement, denoted by x, approaches zero. Specifically, it is demonstrated that $x(N) \rightarrow 0$ as N, representing a cosmic time coordinate, increases. This indicates that, over time, the dilaton field settles towards a minimum, effectively minimizing any violation of the equivalence principle and aligning the model with established physics in the late universe.

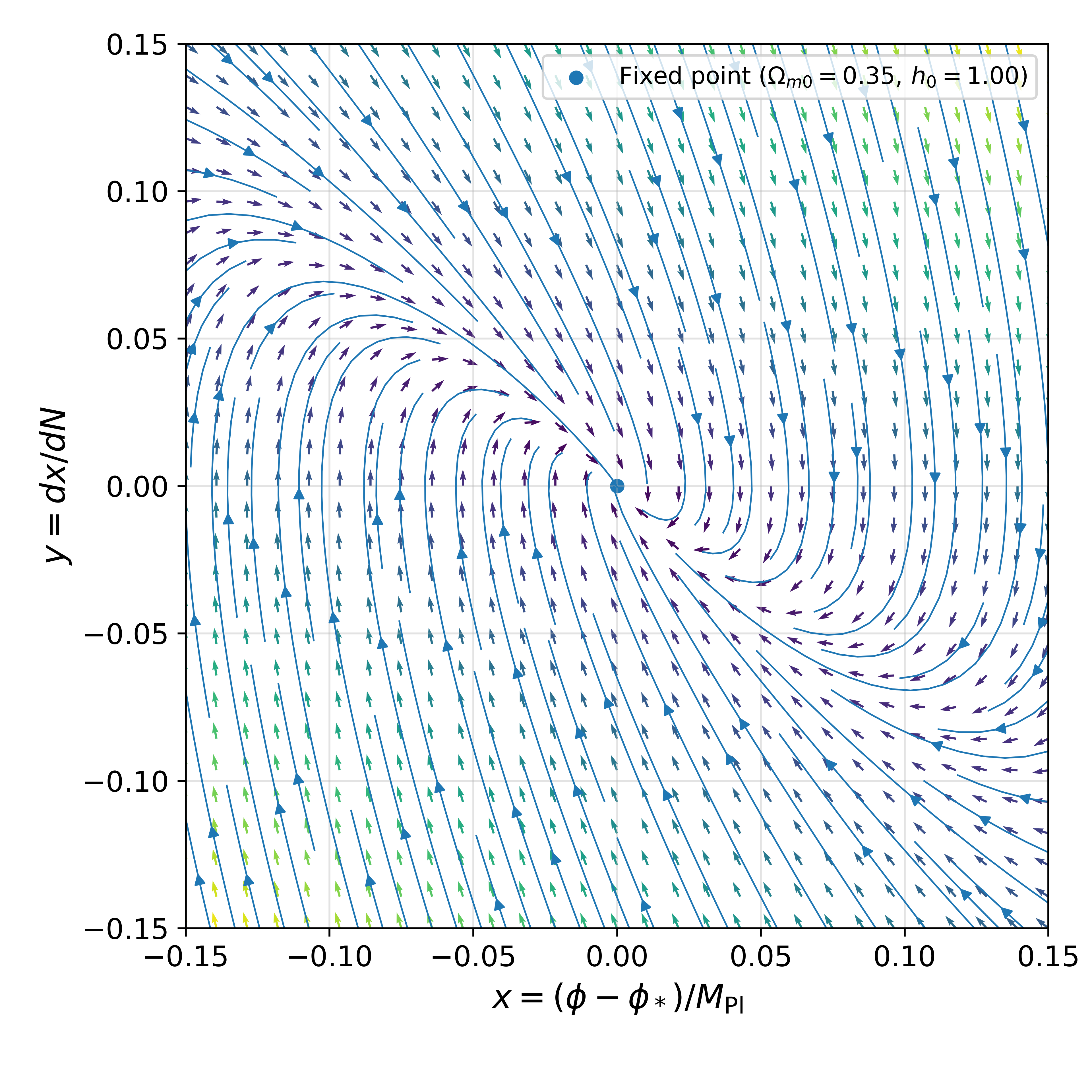
Phase portraits of the linearized Damour-Polyakov system reveal that the least-coupling configuration corresponds to a fixed point at <span class="katex-eq" data-katex-display="false">(0,0)</span>, and its behavior is sensitive to the background matter fraction <span class="katex-eq" data-katex-display="false">\Omega_{m0}</span> (0.25 and 0.32 shown). — Phase portraits of the linearized Damour-Polyakov system reveal that the least-coupling configuration corresponds to a fixed point at $(0,0)$ , and its behavior is sensitive to the background matter fraction $\Omega_{m0}$ (0.25 and 0.32 shown).

The Allure of Stability: The Least-Coupling Point

The Damour-Polyakov expansion is a perturbative technique used to analyze the behavior of the dilaton field in string theory when it couples weakly to matter fields. This expansion is particularly effective near a least-coupling point, defined as a configuration where the dilaton’s interaction with matter is minimized – effectively approaching a fixed point in the renormalization group flow. The method involves expanding physical quantities, such as the effective potential or correlation functions, in terms of $e^{\phi}$ , where φ represents the dilaton field. By systematically including higher-order terms in this expansion, one can obtain increasingly accurate approximations of the dilaton’s dynamics and assess the stability of the resulting cosmological solution, even in regimes where direct calculations are intractable. The power of this technique lies in its ability to provide a controlled approximation scheme for analyzing strongly coupled systems by leveraging the weak coupling limit achievable at the least-coupling point.

The Damour-Polyakov expansion enables the calculation of Jacobian eigenvalues, $λ\pm$ , which directly govern the stability and relaxation rate of the dilaton field. Analysis reveals that the real parts of both eigenvalues, Re( $λ\pm$ ), are negative. A negative real component for both eigenvalues signifies a stable fixed point, indicating that perturbations around this point will decay over time, and the dilaton field will converge towards this stable configuration rather than oscillate or diverge. This stability is crucial for determining the long-term behavior of the dilaton and its influence on cosmological solutions.

Analysis of the Jacobian eigenvalues $\lambda_{\pm}$ provides insight into the long-term behavior of the dilaton field. A negative real component for both eigenvalues, as observed (Re( $\lambda_{\pm}$ ) < 0), indicates that perturbations around the least-coupling point are damped, resulting in the dilaton field relaxing towards a stable fixed point. Conversely, positive or zero real components would suggest instability or oscillatory behavior. This stabilization of the dilaton field is crucial because its value directly influences the effective gravitational constant and other cosmological parameters, thereby impacting the overall evolution and characteristics of the resulting Cosmological Solution.

Whispers of a Fifth Force: Implications and Observables

The existence of a non-zero dilaton field, coupled with a breakdown of the Universal Coupling principle, predicts the potential emergence of a Fifth Force – a fundamental interaction beyond the currently established four. This force wouldn’t interact with all matter equally, but rather would couple differently based on composition, leading to subtle deviations in gravitational experiments. Precision measurements, such as those examining the equivalence principle – the idea that all objects fall at the same rate regardless of mass – become crucial testing grounds. Researchers hypothesize that violations of this principle, even at extremely small scales, could reveal the presence of this Fifth Force, offering a pathway to probe physics beyond the Standard Model and potentially unlocking insights into the nature of dark energy and modified gravity. Detecting this force requires extremely sensitive instrumentation capable of measuring minute variations in gravitational interactions, pushing the boundaries of experimental physics.

The behavior of a dilaton field, and its subtle interactions with matter, are profoundly shaped by the chosen coordinate system used to describe them. Physicists often employ two primary frameworks: the Jordan Frame and the Einstein Frame. In the Jordan Frame, the dilaton appears as a dynamic scalar field directly influencing gravitational coupling, potentially altering the effective gravitational constant. Conversely, the Einstein Frame transforms the dilaton into a field that doesn’t directly affect gravity, but instead manifests as a curvature of spacetime itself, requiring a redefinition of the metric. Understanding these frame-dependent descriptions is crucial because observables – like the strength of a potential Fifth Force – will differ significantly depending on which frame is used for calculations and experimental interpretation; effectively, the dilaton’s coupling to matter isn’t an intrinsic property, but rather a relational one defined by the observer’s perspective within spacetime.

The theoretical implications of a varying dilaton field extend to a potentially observable Fifth Force, and researchers have quantified its expected contribution to experimental measurements. Specifically, the deviation of gravitational force between objects is predicted to scale proportionally to $\alpha_{env} v^2$ , where $\alpha_{env}$ represents the strength of the dilaton’s coupling to matter and $v$ signifies the relative velocity between the interacting masses. This relationship translates to a measurable difference in the ratio of gravitational to inertial mass – expressed as (mg(p)/min – 1) – offering a direct pathway for experimental verification. Precision tests, such as torsion balance experiments or those utilizing advanced atomic interferometry, could thus detect this subtle deviation and provide crucial evidence for or against the existence of a non-zero dilaton field and the associated Fifth Force.

The pursuit of understanding dilaton gravity, as detailed in this work, reveals a humbling truth about theoretical constructs. It’s a venture into regimes where established principles, like the equivalence principle, aren’t immutable laws, but rather approximations valid within a limited scope. As Richard Feynman observed, “The first principle is that you must not fool yourself – and you are the easiest person to fool.” This investigation, employing dynamical systems to trace the evolution of the dilaton field, acknowledges the potential for these approximations to break down. The study demonstrates how the field’s relaxation-or lack thereof-dictates deviations from expected gravitational behavior, reminding one that even the most refined models are susceptible to vanishing beyond the event horizon of reality, much like simplified models becoming ‘pocket black holes’ when confronted with the abyss of cosmological scales.

Where Do We Go From Here?

This work, employing dynamical systems to probe the equivalence principle within dilaton gravity, reveals a landscape both mathematically compelling and deeply unsettling. The Damour-Polyakov mechanism, as explored here, suggests that deviations from general relativity are not merely theoretical curiosities, but potentially observable consequences of a relaxing scalar field. Yet, the very act of constructing such a model necessitates simplification – a reduction of complexity that, while mathematically tractable, may obscure fundamental aspects of the underlying physics. Any such reduction requires strict mathematical formalization, lest the model become a self-deceiving exercise in elegant formalism.

Future investigations must confront the limitations inherent in treating the dilaton as a classical field. A full quantum treatment, connecting the dilaton’s evolution to Hawking radiation and other quantum gravitational effects, remains a formidable challenge. Moreover, the cosmological relaxation of the dilaton is predicated on specific initial conditions; exploring the robustness of this assumption, and the potential for alternative relaxation mechanisms, is crucial.

Ultimately, this line of inquiry serves as a potent reminder: a model, however sophisticated, is merely a map, not the territory. The true nature of gravity, and its connection to the deeper structure of spacetime, may lie beyond the reach of any current theoretical framework. The event horizon, in this context, is not just a boundary in spacetime, but a limit to knowledge itself.

Original article: https://arxiv.org/pdf/2601.20156.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

The Universe’s Hidden Dial: Introducing the Dilaton

Mapping the Cosmos: The FLRW Framework

The Allure of Stability: The Least-Coupling Point

Whispers of a Fifth Force: Implications and Observables

Where Do We Go From Here?

See also: