Author: Denis Avetisyan
A new physics-informed approach leverages the unique properties of radar coherence to reliably identify subtle changes in terrain materials, even in challenging conditions.
Research demonstrates coherence-aware methods consistently outperform intensity-based techniques for terrain material change detection using integral equation modeling and robust statistical analysis.
Detecting subtle terrain material changes in radar imagery remains challenging due to noise and decorrelation effects. This research, presented in ‘Physics-Informed Anomaly Detection of Terrain Material Change in Radar Imagery’, investigates physics-informed approaches to enhance change detection performance. Results demonstrate that incorporating interferometric coherence and robust statistical measures significantly improves the identification of material alterations-shifts in permittivity, roughness, or moisture-particularly in the presence of non-Gaussian clutter. Can these coherence-aware techniques be further refined to enable robust and reliable terrain change monitoring in real-world applications?
Unveiling Change: The Foundation of Critical Observation
The ability to discern alterations in terrain composition through radar data is increasingly vital for a range of critical applications. Beyond simply mapping landscapes, this technology underpins effective disaster monitoring, allowing for rapid assessment of landslides, flood inundation, and volcanic activity. Environmental assessment also benefits significantly; tracking deforestation, glacial retreat, and desertification relies on the precise identification of material changes over time. Furthermore, infrastructure monitoring – detecting subsidence or structural damage – and resource management, such as tracking mineral extraction or agricultural land use, are all fundamentally dependent on the reliable detection of these shifts in terrain characteristics. Consequently, advancements in this field directly contribute to enhanced preparedness, mitigation efforts, and informed decision-making across numerous sectors.
Conventional techniques for identifying landscape alterations using radar imagery face significant challenges due to the intrinsic limitations of the technology. Radar signals are naturally susceptible to noise – random fluctuations that obscure true changes – and variability stemming from factors like atmospheric conditions and the surface roughness of the terrain. This often results in false positives, where the system incorrectly flags an area as changed when it hasn’t, or, conversely, missed events, failing to detect actual alterations on the ground. Consequently, researchers continually strive to develop more robust algorithms capable of distinguishing genuine changes from these confounding factors, ensuring reliable data for critical applications such as disaster response and environmental monitoring.
Modeling the Signal: A Physics-Informed Approach
Radar backscatter is fundamentally governed by the interaction of electromagnetic waves with a surface, a process heavily dependent on both the physical characteristics of that surface and the dielectric properties of its constituent materials. Surface roughness, specifically variations in height relative to the radar wavelength, dictates the degree of scattering – smoother surfaces tend to exhibit specular reflection, while rougher surfaces cause diffuse scattering. Simultaneously, the complex permittivity \epsilon = \epsilon' - j\epsilon'' of the material, comprising a real component representing energy storage and an imaginary component representing energy loss, influences the strength and phase of the returned signal. Variations in permittivity, due to material composition or moisture content, directly affect the radar cross-section and contribute to differences in backscatter intensity. Consequently, accurate modeling of radar returns requires precise characterization of both surface topography and material dielectric constants.
Integral Equation Models (IEM) formulate the radar return problem as an integral equation relating the observed scattered field to the terrain’s dielectric properties and surface geometry. These models, derived from Maxwell’s equations, avoid explicit boundary condition application by expressing the field as a superposition of currents induced on the scattering surface. Common IEM formulations include the Electric Current Method (ECM) and the Magnetic Current Method (MCM), each offering computational advantages depending on the radar frequency and terrain characteristics. The solution to the integral equation, typically obtained through numerical methods like the Method of Moments (MoM), yields the induced currents, which are then used to calculate the scattered field and ultimately the radar return signal; this allows for a direct connection between measurable terrain parameters – such as roughness, slope, and dielectric constant – and the resulting radar backscatter.
Accurate forward models are critical components in radar remote sensing, enabling the prediction of radar return signals given specific terrain and material properties. These models are frequently implemented using Monte Carlo simulation due to the complexity of accurately representing scattering phenomena; this method involves simulating the paths of numerous radar pulses as they interact with the surface, accounting for variations in incidence angle, polarization, and surface characteristics. By generating a statistically representative distribution of return signals, Monte Carlo techniques allow for the estimation of expected radar responses and facilitate the differentiation of true signal from random noise, improving the accuracy of terrain characterization and target detection. The fidelity of these models directly impacts the reliability of radar-based analyses, particularly in scenarios involving complex terrain or heterogeneous dielectric properties.
Robust Statistics for Reliable Anomaly Detection
Radar data frequently exhibits heavy-tailed clutter distributions, meaning the probability of observing extreme values is significantly higher than predicted by traditional Gaussian models. This characteristic poses a challenge for standard statistical techniques, such as those relying on the assumption of normally distributed noise, because these methods underestimate the likelihood of outliers. Consequently, outlier detection performance degrades, leading to increased false alarm rates and reduced sensitivity to weak signals. The deviation from Gaussianity is often caused by non-Rayleigh fading multipath, digital modulation interference, and anomalous propagation conditions, all contributing to the presence of high-amplitude clutter returns that are not adequately accounted for by conventional statistical approaches.
Robust covariance estimators address limitations of sample covariance matrices when dealing with datasets containing outliers or non-Gaussian distributions. Traditional covariance estimation is highly sensitive to these factors, leading to inaccurate representations of data spread and potentially poor detection performance. Tyler’s M-Estimator, a specific robust estimator, minimizes a different cost function than the standard method, reducing the influence of extreme values. This is achieved through iterative weighting of data points, down-weighting those considered outliers during each iteration. Consequently, the resulting covariance matrix provides a more stable and reliable estimate of data scatter in the presence of noise and anomalies, improving the accuracy of subsequent statistical analyses such as Mahalanobis distance calculations.
The RX Detector utilizes the Mahalanobis distance as its primary metric for anomaly detection, quantifying the distance between a data point and the expected distribution based on estimated covariance. To mitigate the impact of outliers and non-Gaussian noise commonly found in radar data, the RX Detector employs robust covariance estimation techniques. This approach calculates a \chi^2 statistic based on the Mahalanobis distance and compares it to a predefined threshold. By using a robust covariance estimator, the threshold is more stable and less susceptible to being influenced by extreme values, thereby reducing the false alarm rate compared to detectors relying on traditional covariance matrices.
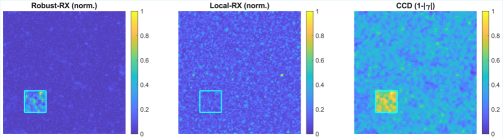
Validating Performance: Addressing System-Level Effects
Speckle noise is an inherent characteristic of Synthetic Aperture Radar (SAR) imagery, originating from the coherent processing of backscattered signals. This granular interference pattern appears as random variations in brightness and is fundamentally linked to the wavelength of the radar and the surface characteristics of the observed area. Critically, the magnitude of speckle noise is inversely proportional to the number of independent looks; increasing the number of looks-through multiple imaging passes or signal averaging-reduces the variance of the speckle, but does not eliminate it entirely. This relationship means that while more looks improve image quality by decreasing speckle’s influence on feature detection, algorithms must still account for residual speckle effects to avoid false positives in change detection or anomaly identification.
Coherent Change Detection (CCD) leverages the phase difference between two Synthetic Aperture Radar (SAR) images – known as interferometric coherence – to identify areas of change; however, the accuracy of CCD is significantly impacted by speckle noise, an inherent characteristic of radar imagery. Speckle manifests as random variations in backscatter and reduces coherence, potentially leading to false positive change detections. Therefore, successful implementation of CCD necessitates careful consideration of system parameters such as wavelength, polarization, and baseline separation, as these factors directly influence coherence and, consequently, the sensitivity and reliability of change detection results. Mitigation strategies often involve multi-looking techniques or filtering to reduce speckle, but these must be balanced against a reduction in spatial resolution.
Unsupervised Auto-Encoders (AE) represent a data-driven methodology for anomaly detection that relies on learning a compressed representation of normal system behavior. The effectiveness of AE models is directly correlated with the quantity and quality of training data; insufficient or biased data can lead to poor generalization and reduced detection capability. Furthermore, given the inherent speckle noise present in Synthetic Aperture Radar (SAR) imagery, pre-processing techniques or architectural modifications within the AE are necessary to mitigate the impact of this noise and prevent it from being misinterpreted as anomalous behavior. Proper handling of speckle is crucial for achieving reliable anomaly detection performance with AE-based systems.
Monte Carlo simulations were conducted to evaluate the performance of various change detection methodologies. Results indicated that coherence-centric methods – specifically Coherent Change Detection (CCD) and a simple score-level fusion of coherence information – consistently outperformed intensity-based detectors, namely RX and Local-RX. This superiority was quantified through Area Under the Receiver Operating Characteristic curve (ROC-AUC) and Area Under the Precision-Recall curve (PR-AUC) metrics, where CCD and score-level fusion achieved the highest values. These metrics demonstrate that coherence-centric approaches exhibit improved discrimination between actual changes and noise, leading to more accurate detection capabilities compared to methods relying solely on signal intensity.
Evaluation metrics from Monte Carlo simulations indicate that Coherent Change Detection (CCD) and a score-level fusion of CCD with other methods yielded the highest F1 scores when the Probability of False Alarm (PFA) was fixed at 10-3. The F1 score, calculated as the harmonic mean of precision and recall, provides a balanced measure of a detector’s performance. Achieving the highest F1 score at this PFA level demonstrates that CCD and the score-level fusion approach offer superior detection capability compared to the intensity-based detectors tested, specifically RX and Local-RX, under the defined experimental conditions.
The research highlights a critical aspect of signal processing: the necessity of understanding underlying physical models to achieve robust detection. This aligns with John Dewey’s assertion that, “Education is not preparation for life; education is life itself.” Just as a comprehensive education requires understanding foundational principles, this work demonstrates that coherence-aware change detection, grounded in an integral equation model, provides a more ‘living’ and accurate representation of terrain material changes than methods solely reliant on intensity. The consistent outperformance in non-Gaussian clutter underscores that algorithmic choices are never neutral; they embody assumptions about the world and, therefore, carry social consequences-in this case, improved accuracy in environmental monitoring and terrain analysis.
Where Do We Go From Here?
The demonstrated efficacy of coherence-aware change detection, while promising, merely reframes a more fundamental question: what constitutes ‘change’ itself? This work rightly prioritizes the detection of material property shifts, but neglects to interrogate the inherent assumptions embedded within that very definition. Optimizing for sensitivity to terrain alteration, without considering the ecological or anthropogenic contexts driving those alterations, feels like a refinement of a tool without a clear understanding of its ultimate purpose.
Future efforts must move beyond signal processing gains and grapple with the complexities of interpretation. Robust statistical methods, while valuable for mitigating noise, cannot resolve ambiguity in intent. A pixel flagged as ‘changed’ represents not an objective truth, but a probabilistic assertion, susceptible to the biases of the modeling choices made. The pursuit of ever-finer detection thresholds risks amplifying trivial variations while obscuring meaningful trends, effectively automating a form of hyper-vigilance divorced from contextual understanding.
Ultimately, the field’s trajectory hinges on acknowledging that algorithmic bias is not a bug, but a mirror reflecting the values – or lack thereof – encoded within the system. Transparency is the minimum viable morality, yet it is insufficient. A truly progressive approach demands a critical examination of what is being optimized for, why, and for whom – questions that extend far beyond the realm of integral equation models and interferometric coherence.
Original article: https://arxiv.org/pdf/2602.15618.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- How to Get to Heaven from Belfast soundtrack: All songs featured
- 10 Best Anime to Watch if You Miss Dragon Ball Super
- 10 Most Memorable Batman Covers
- Ashes of Creation Mage Guide for Beginners
- How to Froggy Grind in Tony Hawk Pro Skater 3+4 | Foundry Pro Goals Guide
- Wife Swap: The Real Housewives Edition Trailer Is Pure Chaos
- The USDH Showdown: Who Will Claim the Crown of Hyperliquid’s Native Stablecoin? 🎉💰
- 7 Best Animated Horror TV Shows
- The Best Members of the Flash Family
2026-02-18 19:13