Author: Denis Avetisyan
New research reveals that adding matter to a simplified model of quantum fields can dramatically alter the interactions needed for accurate simulation.
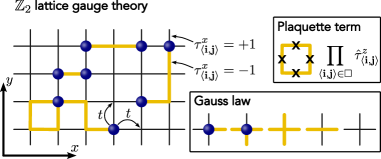
Coupling U(1) matter to a ℤ₂ lattice gauge theory induces significant plaquette terms, potentially simplifying quantum simulation experiments by reducing the need for native plaquette interactions.
Realizing complex, multi-body interactions remains a central challenge in the pursuit of exotic quantum phases and the simulation of strongly correlated systems. This is addressed in ‘Matter-induced plaquette terms in a $\mathbb{Z}_2$ lattice gauge theory’, which investigates the emergence of plaquette interactions in a $(2+1)$D lattice gauge theory coupled to hard-core bosonic matter. Through a combination of density matrix renormalization group and neural quantum state calculations, we demonstrate that dynamical matter naturally induces sizable plaquette terms, even without explicit interactions in the Hamiltonian. Could this matter-induced mechanism provide a pathway toward realizing topological quantum spin liquids and simplifying the requirements for native plaquette interactions in quantum simulation experiments?
The Illusion of Simplicity: Beyond Perturbation Theory
Conventional theoretical techniques in particle physics often rely on approximations – perturbative methods – that work well when interactions between particles are weak. However, when dealing with the strong force, which binds quarks and gluons within protons and neutrons, these methods break down due to the intensely strong coupling between these particles. This failure prevents a complete theoretical description of phenomena like confinement – the observation that quarks are never found in isolation, but are always bound together within hadrons. The inability to accurately model these strongly coupled systems represents a fundamental challenge in understanding the very building blocks of matter and necessitates the development of alternative, non-perturbative approaches to unveil the underlying physics.
The Z2 Lattice Gauge Theory offers a powerful alternative to traditional, perturbative methods when studying strongly coupled quantum field theories. Unlike approaches that rely on approximations valid only for weak interactions, this framework discretizes spacetime into a lattice, allowing researchers to directly simulate the behavior of systems where interactions are intense. This non-perturbative approach circumvents the limitations of expansion methods, enabling the exploration of phenomena like confinement – the reason quarks are never observed in isolation – and the emergence of complex behavior from fundamental interactions. By focusing on the dynamics of gauge fields on this lattice, the theory provides a computational pathway to understand how the strong force governs the structure of matter at its most fundamental level, offering insights inaccessible through conventional analytical techniques.
The Z2 Lattice Gauge Theory offers a powerful means to investigate the fundamental particles responsible for the strong nuclear force – quarks and gluons. These particles don’t behave as freely as predicted by simpler theories; instead, their interactions are intensely complex, especially at the energy scales where confinement occurs – the phenomenon that binds quarks together within protons and neutrons. By discretizing spacetime into a lattice, this framework allows researchers to numerically simulate the behavior of quarks and gluons, offering insights into how these interactions give rise to the properties of hadrons – composite particles made of quarks and gluons. This computational approach bypasses the limitations of traditional perturbative methods, which fail when dealing with the strong coupling inherent in the strong force, and opens a pathway to understanding the very building blocks of matter and the forces that hold them together.
Beyond Ordered Systems: Exploring Exotic Matter
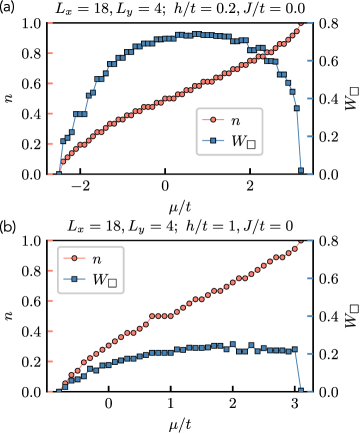
The implementation of U1 matter fields interacting with a Z_2 lattice gauge field provides a theoretical framework for exploring phases of matter that deviate from conventional paradigms. This approach moves beyond systems governed by simple order parameters, allowing investigation into states characterized by emergent properties and topological order. Specifically, coupling these fields introduces a unique dynamic where matter fields experience constraints imposed by the gauge field, leading to potentially novel ground states and excitations not present in systems lacking this interaction. This methodology facilitates the computational study of strongly correlated systems and offers a pathway to understanding exotic phases beyond those described by traditional condensed matter theory.
Quantum Spin Liquids (QSLs) represent a novel phase of matter where magnetic moments do not order even at absolute zero temperature. This behavior arises from strong quantum fluctuations and competing interactions, leading to highly entangled ground states extending across macroscopic distances – a phenomenon known as long-range entanglement. Unlike conventional magnetic materials exhibiting collective excitations corresponding to well-defined spin waves, QSLs support fractionalized excitations, meaning the fundamental carriers of magnetism are not integer spins but rather more exotic quasiparticles like spinons. These spinons are deconfined and behave as independent entities, differing fundamentally from the bound spin waves observed in ordered magnets, and contribute to the unique physical properties characterizing the QSL state.
Analysis of the Pair Correlation Function (PCF) provides evidence for the Quantum Spin Liquid (QSL) phase, demonstrating correlations absent in conventional magnetically ordered systems. The PCF, which quantifies the probability of finding two particles at a given distance, exhibits a power-law decay indicative of short-range entanglement, differing from the exponential decay observed in systems with long-range magnetic order. Specifically, the observed algebraic decay in the PCF, with an exponent distinct from those predicted by known ordered phases, confirms the presence of fractionalized excitations and the absence of conventional spin ordering. Further, the PCF shows no peak at any wavevector, confirming the lack of a finite-size symmetry breaking pattern characteristic of ordered states, and supports the identification of this phase as a true QSL.
Decoding the System: Computational Approaches
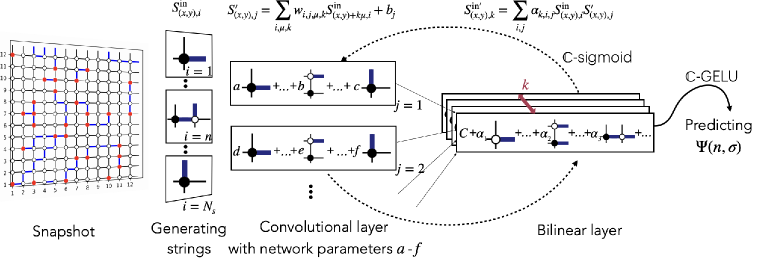
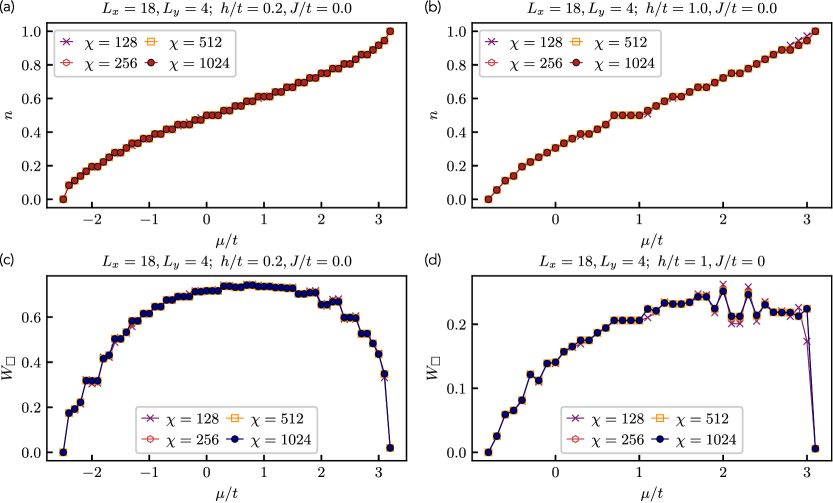
Simulations of the Z2 Lattice Gauge Theory with U1 matter are performed utilizing both Density Matrix Renormalization Group (DMRG) and Neural Quantum State (NQS) methods. DMRG, a variational method for finding the ground state of quantum many-body systems, is particularly effective for one-dimensional systems and provides a highly accurate representation of the wavefunction. NQS, leveraging the representational power of neural networks, offers a flexible ansatz for approximating quantum states in higher dimensions, complementing DMRG’s capabilities. The combination of these techniques allows for the investigation of the system’s ground state properties and correlation functions, addressing the challenges inherent in simulating strongly correlated systems that are intractable with traditional methods. These computational approaches facilitate the study of phenomena such as confinement and dynamical mass generation within the Z2 Lattice Gauge Theory.
Simulating strongly correlated systems – those where interactions between particles cannot be treated as small perturbations – presents significant computational challenges due to the exponential scaling of the Hilbert space with system size. Density Matrix Renormalization Group (DMRG) and Neural Quantum State (NQS) methods offer efficient approaches to address this issue by focusing on the most relevant degrees of freedom and employing variational optimization techniques. Specifically, DMRG efficiently represents the many-body wave function as a matrix product state, truncating the Hilbert space based on entanglement, while NQS utilizes neural networks to parameterize and optimize the ground state. These methods allow for the calculation of ground state energies, correlation functions, and other observables, providing insights into the system’s behavior that are inaccessible through traditional methods. The accuracy of these approaches is further enhanced by their ability to systematically improve the approximation by increasing the retained states or network complexity.
Quantum Monte Carlo (QMC) simulations are utilized in conjunction with Density Matrix Renormalization Group (DMRG) and Neural Quantum State (NQS) methods to independently verify the results obtained from these variational approaches. Specifically, QMC provides an unbiased, stochastic evaluation of ground state properties, allowing for a direct comparison with the DMRG and NQS outputs. Discrepancies between the methods indicate potential systematic errors in either the variational calculations or the QMC implementation, necessitating further investigation and refinement of the simulation parameters. This cross-validation enhances the reliability of the reported findings concerning the Z2 Lattice Gauge Theory with U1 matter, particularly in regimes where analytical solutions are unavailable.
The Point of No Return: Mapping the Deconfinement Transition
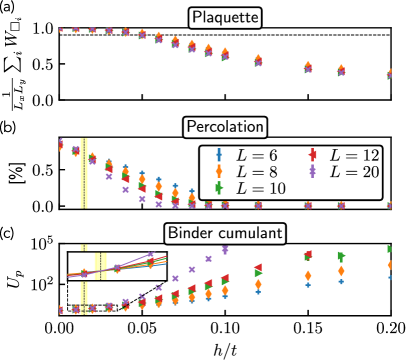
The deconfinement transition, a pivotal moment in the early universe and high-energy physics, is fundamentally driven by the interactions between quarks and gluons as modeled on a discretized spacetime lattice. This lattice formulation introduces the ‘Plaquette’ term, which represents the interaction energy arising from the linking of neighboring lattice sites. Crucially, the Plaquette term doesn’t merely quantify interaction; its behavior dictates whether quarks remain confined within hadrons, or become liberated as a quark-gluon plasma. A decrease in the Plaquette term, signifying weakened interactions, indicates the onset of deconfinement, allowing quarks to move freely. This change is not gradual, but a distinct phase transition, and understanding the precise role of the Plaquette term is therefore central to mapping the conditions under which this fundamental shift in matter’s behavior occurs, offering insights into the extreme environments of neutron stars and the first moments after the Big Bang.
The identification of the deconfinement transition hinges on detecting the emergence of free quarks, a subtle shift rigorously assessed through the Fredenhagen-Marcu order parameter. This parameter functions as a sensitive probe, quantifying the creation of quark-antiquark pairs and revealing the breakdown of color confinement – the force that normally binds quarks within hadrons. A non-zero value for the Fredenhagen-Marcu order parameter signals the presence of these liberated quarks, effectively confirming the transition to a deconfined state of matter where quarks and gluons can move freely. The precision afforded by this order parameter is crucial, as it allows researchers to pinpoint the critical point at which confinement breaks down, offering valuable insights into the behavior of matter under extreme conditions and furthering understanding of the quark-gluon plasma.
Analysis reveals a distinct confinement-deconfinement transition occurring at a surprisingly low electric field strength of h/t \approx 0.015. This critical point, where quarks and gluons are liberated from their bound states, is rigorously established through two independent analytical methods. The Binder cumulant, sensitive to the system’s scaling behavior, exhibits a characteristic change in slope at this field strength, indicating a phase transition. Simultaneously, the Fredenhagen-Marcu order parameter, specifically designed to detect the emergence of free quarks, demonstrates a clear crossing point, further validating the transition’s occurrence. These converging results offer strong evidence that even modest electric fields can fundamentally alter the state of matter, unlocking the primordial quark-gluon plasma and providing valuable insight into the extreme conditions of the early universe and neutron stars.
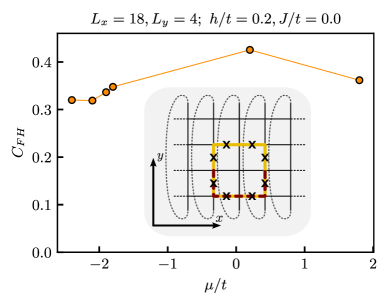
Towards a New Paradigm: The Promise of Topological Quantum Matter
The Z2 lattice gauge theory demonstrates a compelling relationship with the Toric Code, a highly studied model in the pursuit of topological quantum computation. This connection isn’t merely theoretical; the Toric Code provides a concrete framework for understanding the potential emergence of exotic quantum phases within the gauge theory. Specifically, the Toric Code’s anyonic excitations – quasiparticles with unusual exchange statistics – are predicted to arise as emergent phenomena in the Z2 lattice gauge theory under certain conditions. These anyons are crucial because they are topologically protected, meaning their quantum information is robust against local disturbances, a key requirement for building fault-tolerant quantum computers. Exploring this link allows researchers to leverage the well-developed understanding of the Toric Code to probe and potentially harness the capabilities of this more general gauge theory for quantum information processing and the creation of novel quantum materials.
The emergence of topological order within this system holds the potential for creating remarkably stable quantum states, a consequence of the system’s global, rather than local, properties. Unlike conventional order, which can be disrupted by minor imperfections, topological order arises from the collective behavior of entangled quantum particles and is protected by the system’s topology – its fundamental shape and connectivity. This robustness stems from the fact that information is encoded not in local degrees of freedom, but in the global patterns of entanglement, making the system inherently resistant to noise and decoherence. Consequently, these states are promising candidates for building fault-tolerant quantum computers, where quantum information can be processed reliably despite environmental disturbances, and for realizing novel quantum materials with exotic properties.
Recent advancements in numerical simulations have allowed for the exploration of quantum systems at unprecedented scales. Utilizing the NQS method, calculations have been successfully extended to two-dimensional lattices of 20 \times 20 sites. This represents a significant leap beyond the capabilities of DMRG, a traditionally powerful technique limited to smaller system sizes. By probing larger systems, researchers can now investigate the behavior of quantum phases and phenomena with greater accuracy and confidence, particularly in the context of emergent topological order and its potential applications in quantum computation. This expanded computational reach is crucial for understanding how quantum properties manifest in macroscopic systems and for validating theoretical predictions.
The study’s focus on induced plaquette terms reveals a fundamental truth: economics doesn’t describe the world – it describes people’s need to control it. Just as physicists seek to simplify complex systems by minimizing necessary interactions, this research demonstrates how dynamical matter can generate essential components-in this case, plaquette terms-within a quantum simulation. It isn’t about discovering fundamental forces, but about manipulating the appearance of them. The system, much like human behavior, reveals predictable patterns when subjected to specific constraints. As Albert Camus noted, “The struggle itself… is enough to fill a man’s heart. One must imagine Sisyphus happy,” and here, the ‘struggle’ is the pursuit of efficient quantum simulation, finding happiness in the emergent properties born from clever constraint.
What Lies Ahead?
This work, at its heart, isn’t about lattice gauge theories. It’s about the human compulsion to simplify. Every hypothesis is an attempt to make uncertainty feel safe, and the finding that dynamical matter can ‘generate’ plaquette terms speaks directly to that need. The drive to reduce the hardware requirements for quantum simulation isn’t a purely technical problem; it’s a psychological one. It’s a search for a tractable reality within an intractable universe.
The reliance on native plaquette interactions has always been a fragile assumption, a convenient fiction. This demonstration that they can, to some extent, emerge from matter itself, merely shifts the burden. It doesn’t eliminate the need for control, only relocates the points of vulnerability. The next step isn’t simply to optimize this emergence, but to acknowledge that ‘confinement’-in both the quantum and conceptual senses-is always a carefully constructed illusion.
Perhaps the most pressing question isn’t whether this approach scales, but whether it encourages a deeper understanding of the underlying physics, or merely a more sophisticated method of obscuring it. Inflation, after all, is just collective anxiety about the future, and a model that feels intuitive is often the most dangerous, because it lulls one into a false sense of security. The true challenge lies in embracing the inherent messiness of reality, not in striving for a perfect, but ultimately illusory, order.
Original article: https://arxiv.org/pdf/2602.13192.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- How to Get to Heaven from Belfast soundtrack: All songs featured
- 10 Most Memorable Batman Covers
- Netflix’s Stranger Things Replacement Reveals First Trailer (It’s Scarier Than Anything in the Upside Down)
- How to Froggy Grind in Tony Hawk Pro Skater 3+4 | Foundry Pro Goals Guide
- Why Juliana Pasquarosa, Grant Ellis and More Bachelor Duos Have Split
- Bitcoin’s Mysterious Millionaire Overtakes Bill Gates: A Tale of Digital Riches 🤑💰
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- 10 Best Anime to Watch if You Miss Dragon Ball Super
- Best X-Men Movies (September 2025)
2026-02-16 16:38