Simulating Quantum Fields with Ultracold Atoms

by

Author: Denis Avetisyan

Researchers demonstrate a promising pathway to quantum simulate 2+1D quantum electrodynamics using tunable optical lattices and trapped atoms.

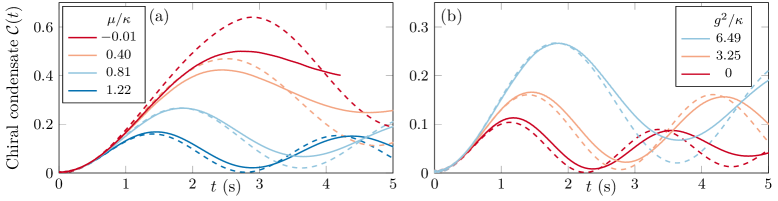
Numerical simulations explore the dynamic evolution of chiral condensates in a proposed quantum simulator of the (2+1)-dimensional spin-1 quantum liquid magnet, demonstrating how manipulation of the staggering potential δ - ranging from 79.49 to 79.64 Hz - and the electric field energy <span class="katex-eq" data-katex-display="false">g^2</span>, achieved through coordinated adjustments to both on-site interactions <span class="katex-eq" data-katex-display="false">U</span> and δ, influences the system’s response to quenching from the vacuum state on an infinite cylinder with a width of two matter sites.
Numerical simulations explore the dynamic evolution of chiral condensates in a proposed quantum simulator of the (2+1)-dimensional spin-1 quantum liquid magnet, demonstrating how manipulation of the staggering potential δ – ranging from 79.49 to 79.64 Hz – and the electric field energy g^2, achieved through coordinated adjustments to both on-site interactions U and δ, influences the system’s response to quenching from the vacuum state on an infinite cylinder with a width of two matter sites.

The study benchmarks a quantum simulation of the 2+1D spin-1 U(1) quantum link model, leveraging the Bose-Hubbard model and confirming gauge invariance.

Simulating quantum field theories on near-term quantum devices remains a significant challenge, particularly in higher spatial dimensions. This work, ‘Towards $2+1$D quantum electrodynamics on a cold-atom quantum simulator’, proposes a feasible scheme for realizing a $(2+1)$-dimensional U$(1)$ lattice gauge theory using a spin-$1$ truncation within a cold-atom platform. By mapping the theory onto a bosonic computational basis stabilized by a quantum Zeno-effect-driven gauge protection mechanism and implementing it via a tilted optical superlattice Bose-Hubbard model, we demonstrate faithful real-time dynamics and preservation of gauge constraints using infinite matrix product state simulations. Could this approach pave the way for exploring more complex phenomena in higher-dimensional quantum electrodynamics with accessible experimental resources?

The Inevitable Limits of Approximation

Gauge theory, the cornerstone of the Standard Model of particle physics, successfully describes fundamental forces and the interactions of elementary particles. Beyond its role in the Standard Model, this theoretical framework extends to explain a vast array of emergent phenomena, from the properties of superfluids to the behavior of quarks and gluons in extreme conditions. However, a significant obstacle arises when attempting to make precise, quantitative predictions – particularly in the realm of ‘non-perturbative’ calculations. These calculations, essential for understanding strong interactions where forces aren’t weak enough to allow for simple approximations, are computationally intractable using traditional methods. The inherent complexity stems from the strong coupling constants governing these interactions, rendering standard perturbative expansions unreliable and necessitating alternative, more sophisticated approaches to unravel the intricacies of strongly coupled systems.

Lattice Gauge Theory provides a unique, computationally intensive approach to solving problems in quantum chromodynamics and other gauge theories, traditionally intractable through analytical methods. This technique fundamentally reimagines spacetime not as a continuous entity, but as a four-dimensional grid – a lattice – allowing for the discretization of quantum fields. By representing fields at discrete points, complex interactions can be translated into manageable numerical calculations performed on high-performance computers. This discretization transforms the mathematical challenge of solving differential equations into an algebraic one, enabling physicists to simulate the behavior of quarks and gluons, and thereby explore the strong force with unprecedented detail. Though demanding in terms of computational resources, LGT offers a pathway to understanding non-perturbative regimes of gauge theories, offering insights into phenomena like confinement and the properties of hadrons.

Lattice Gauge Theory, while promising for calculating the properties of strongly interacting matter, encounters a significant hurdle when simulating conditions with non-zero baryon density – the so-called ‘Sign Problem’. Monte Carlo methods, essential for these calculations, rely on generating configurations weighted by a Boltzmann factor, but at finite density, this factor becomes complex. Consequently, the simulations suffer from cancellations, leading to exponentially decreasing signal-to-noise ratios and rendering meaningful calculations intractable. This severely restricts the exploration of phenomena such as neutron star interiors, the quark-gluon plasma created in heavy-ion collisions, and the behavior of matter under extreme conditions, as these systems inherently involve finite baryon density and require a robust understanding of strongly coupled dynamics.

The persistent challenges posed by the Sign Problem in Lattice Gauge Theory have spurred significant investigation into novel computational strategies. Researchers are actively exploring alternative mathematical formulations of quantum chromodynamics, seeking to circumvent the issue of complex phase cancellations that plague standard Monte Carlo simulations. These efforts include investigations into different discretization schemes, improved sampling algorithms, and even completely new theoretical frameworks, such as complex Langevin dynamics and tensor networks. The goal is to develop methods capable of reliably simulating strongly coupled systems at finite baryon density – a crucial step toward understanding the behavior of matter under extreme conditions, like those found in neutron stars and heavy-ion collisions, and ultimately refining the Standard Model of particle physics.

Numerical simulations of quenches in a (2+1)-dimensional spin-1 quantum spin liquid model demonstrate the evolution of the chiral condensate, matching the behavior of a Bose-Hubbard simulator across varying staggering potentials δ from 79.39 to 79.54 Hz.
Numerical simulations of quenches in a (2+1)-dimensional spin-1 quantum spin liquid model demonstrate the evolution of the chiral condensate, matching the behavior of a Bose-Hubbard simulator across varying staggering potentials δ from 79.39 to 79.54 Hz.

Recasting the Problem: A Many-Body Approach

The Hamiltonian Formulation of Lattice Gauge Theory (LGT) diverges from the conventional approach by recasting the problem as a quantum many-body system amenable to techniques used in condensed matter physics. Traditional LGT relies on path integral methods to calculate physical observables, which encounter significant computational challenges – notably the sign problem – when simulating systems at non-zero chemical potential or finite density. By representing the gauge fields as dynamical variables within a Hamiltonian framework, this formulation avoids direct reliance on path integrals and instead describes the system’s evolution in terms of operators acting on a Hilbert space. This allows for the application of established quantum many-body methods, such as diagonalization, quantum Monte Carlo, or variational techniques, to study non-equilibrium dynamics and static properties of strongly coupled gauge theories.

Traditional Lattice Gauge Theory (LGT) calculations rely on path integrals, which become computationally intractable when simulating systems at finite density due to the “sign problem” – the exponential growth of complex phases canceling out contributions to the integral. The Hamiltonian formulation of LGT circumvents this issue by reformulating the theory as a quantum many-body problem, directly operating on Hilbert space. This avoids the need for path integration and associated complex phase cancellations, allowing for simulations of systems with non-zero baryon or isospin chemical potential – a critical capability for studying dense matter physics, such as that found in neutron stars or in heavy-ion collisions. While computationally demanding in its own right, this approach offers a potential pathway to overcoming the limitations imposed by the sign problem in conventional LGT.

The Quantum Link Model (QLM) represents a fundamental shift in how gauge fields are treated within the Hamiltonian formulation of Lattice Gauge Theory. Instead of continuous variables, the gauge field – typically represented by a link variable U_{\mu}(x) – is discretized and mapped onto a finite-dimensional Hilbert space using spin operators. Specifically, each link connecting lattice sites is associated with an operator acting on this space, effectively quantizing the gauge field. These spin operators satisfy local gauge symmetry constraints, ensuring the model retains the essential physics of the original gauge theory. The dimension of the Hilbert space associated with each link is a free parameter, often denoted as ‘d’, and determines the level of discretization. By representing the gauge field with these discrete degrees of freedom, the QLM transforms the problem into a quantum many-body system amenable to numerical simulation using techniques developed for condensed matter physics.

Implementing the Quantum Link Model (QLM) necessitates significant computational resources due to the exponential scaling of the Hilbert space with system size; specifically, each link in the lattice is represented by a spin operator requiring multiple quantum bits for its description. This complexity arises from the need to accurately represent the quantum dynamics of the gauge fields themselves. However, this computational cost unlocks the potential to simulate strongly correlated quantum systems – those where interactions between particles are dominant and traditional perturbative methods fail. These systems, prevalent in areas like high-temperature superconductivity and quark-gluon plasma, are inaccessible to many conventional lattice gauge theory approaches due to the sign problem, which the Hamiltonian formulation aims to circumvent by operating within a well-defined Hilbert space.

Bridging Theory and Experiment: A Matter of Correspondence

The Quantum Lattice Model (QLM) demonstrates a direct correspondence with the Bose-Hubbard Model (BHM), a fundamental framework in condensed matter physics describing interacting bosonic particles arranged on a lattice. The BHM, typically expressed as H = -J \sum_{\langle i,j \rangle} (b^{\dagger}_i b_j + b^{\dagger}_j b_i) + \frac{U}{2} \sum_i n_i(n_i - 1), defines a system where bosons hop between lattice sites with amplitude J and experience on-site interaction strength U. Mapping the QLM onto the BHM allows for the translation of QLM parameters to equivalent BHM parameters, enabling the study of complex quantum phenomena through a well-established theoretical lens. This correspondence facilitates predictions about the QLM’s behavior by leveraging the extensive analytical and numerical tools developed for the BHM, and conversely, provides a platform for experimentally verifying BHM predictions through the QLM.

Mapping the Quantum Lattice Model (QLM) onto a physical system enables researchers to investigate its dynamic properties through experimentation. Ultracold atom experiments provide a controlled environment for simulating the QLM, allowing for observation of time evolution and emergent phenomena. By precisely controlling the parameters of the atomic system – such as lattice spacing and interaction strengths – researchers can directly probe predictions made by the QLM. This experimental validation is crucial for verifying the model’s accuracy and for gaining a deeper understanding of the underlying physics, offering insights not readily accessible through purely theoretical approaches. The ability to observe and quantify the dynamics of the QLM in a real-world system strengthens the model’s predictive power and informs further theoretical development.

The Bose-Hubbard Model (BHM) necessitates controlled, short-range interactions between bosons residing on a lattice. These interactions can be physically implemented using ultracold atoms by leveraging dipole-dipole interactions. Specifically, through techniques such as Feshbach resonances and external magnetic fields, the scattering length between atoms can be tuned, directly controlling the strength of the contact interaction which effectively mimics the on-site interaction term U in the BHM. Furthermore, by employing optical lattices formed by interfering laser beams, a periodic potential is created, confining the atoms and establishing the lattice structure required by the model. The tunneling amplitude J is then determined by the depth of the optical lattice and the atomic mass.

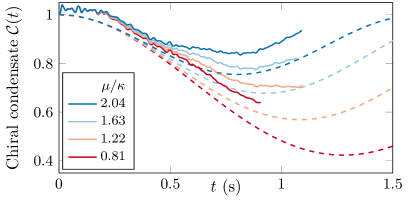
Ultracold atom systems, implemented within optical superlattices, provide a highly controlled experimental platform for validating the predictions of the Quantum Lattice Model (QLM). These superlattices are created using interfering laser beams, forming a periodic potential that confines the atoms and effectively creates an artificial lattice structure. Crucially, the experimental setup is engineered to maintain a gauge violation of less than 0.1% throughout the duration of the quantum simulation. This high degree of gauge symmetry preservation is achieved through precise control of the laser parameters and careful minimization of external perturbations, ensuring the fidelity of the experimental results to the theoretical predictions derived from the QLM. The system allows for detailed observation and quantitative comparison with theoretical models of quantum many-body physics.

Beyond Simulation: Towards a Unified Understanding

The power of these computational explorations resides not solely within the confines of particle physics, but extends into diverse areas of condensed matter research. Simulations originally designed to probe the behavior of fundamental forces are now revealing unexpected connections to exotic states of matter, such as quantum spin liquids and the fractional quantum Hall effect – systems where collective behavior gives rise to emergent gauge fields. This cross-disciplinary application demonstrates the unifying power of theoretical frameworks; the same mathematical tools used to describe interactions between elementary particles are proving remarkably adept at characterizing complex quantum phenomena in materials. Consequently, advancements in simulating high-energy physics are providing new avenues for understanding and potentially engineering novel quantum materials with tailored properties, highlighting a synergistic relationship between seemingly disparate fields of scientific inquiry.

The profound mathematical framework of gauge theories, initially developed to describe fundamental forces in high-energy physics, extends far beyond that realm to illuminate the behavior of complex materials. These theories provide a surprisingly effective lens through which to understand emergent phenomena in condensed matter systems, notably including exotic states like Quantum Spin Liquids and the Fractional Quantum Hall Effect. In Quantum Spin Liquids, magnetic moments avoid conventional ordering even at absolute zero, exhibiting fractionalized excitations governed by emergent gauge fields. Similarly, the Fractional Quantum Hall Effect, observed in two-dimensional electron gases subjected to strong magnetic fields, arises from the collective behavior of electrons forming quasiparticles with fractional charge and obeying peculiar statistics – a direct consequence of emergent gauge interactions. The ability of gauge theories to capture these seemingly disparate phenomena underscores their fundamental role in describing collective behavior and emergent order in a wide range of physical systems.

The creation of artificial gauge fields within ultracold atom systems presents a novel pathway for investigating complex quantum phenomena previously confined to theoretical models. These systems, leveraging the precise control afforded by laser and magnetic trapping techniques, allow researchers to mimic the behavior of particles interacting through fundamental forces, but in a readily observable and tunable environment. Specifically, this approach facilitates the study of exotic states of matter like Quantum Spin Liquids and the Fractional Quantum Hall Effect – materials exhibiting collective quantum behavior and fractionalized excitations. By directly observing the dynamics of these simulated gauge fields and their associated emergent phenomena, scientists are gaining unprecedented insights into the fundamental principles governing condensed matter physics and potentially unlocking new avenues for materials design and quantum technologies.

Recent investigations into quenched dynamics reveal nuanced behaviors between Quantum Lattice Models (QLM) and Bose-Hubbard Models (BHM). Simulations demonstrate a qualitative similarity in their responses when initiated from a vacuum state – a condition of minimal excitation. However, a marked divergence emerges when the quench originates from a charge-proliferated state, indicating a sensitivity to initial conditions. This deviation manifests as a correction to the effective mass of the system, attributable to the influence of forbidden sites within the lattice. Quantitative analysis estimates this correction to be -2J²(1/(7δ+Ρ) + 3/(-δ+Ρ) + 6/(-9δ+Ρ)), where parameters δ and Ρ define characteristics of the lattice and interactions. This finding highlights the critical role of initial state preparation and lattice geometry in controlling the emergent dynamics of these coupled quantum systems.

The pursuit of simulating complex physical systems, as demonstrated in this work with 2+1D quantum electrodynamics, echoes a fundamental truth about all structures. Just as time provides the medium for observing the evolution of a quantum simulation-with deployment marking a specific point on its timeline-systems themselves are subject to the inevitable passage of time. Henry David Thoreau observed, “Time is but the stream I go a-fishing in.” This notion resonates with the study’s approach to benchmarking the quantum simulator against the target gauge theory; it’s an attempt to understand a system’s behavior not as a static entity, but as a dynamic process unfolding within the constraints of its own internal ‘chronicle’, much like the logging inherent in monitoring the simulation’s progress.

What Lies Ahead?

This work, like any attempt to sculpt the ephemeral, reveals as much about the limitations of the tools as the nature of the substance. The demonstrated correspondence between simulated gauge fields and the target theory is a noteworthy calibration, but calibration is not mastery. The inherent challenge remains: these systems do not strive for perfect emulation, but for graceful aging. The question isn’t whether the simulation can perfectly become quantum electrodynamics, but how predictably it degrades from it.

Future iterations will undoubtedly focus on scaling-increasing lattice size, extending simulation times. However, a more subtle path lies in embracing the imperfections. Exploring the emergent phenomena born from the discrepancies-the ‘noise’ in the system-may prove more fruitful than chasing an asymptotic ideal. Sometimes observing the process of decay, the manner in which order surrenders to entropy, is better than trying to indefinitely postpone it.

Ultimately, this approach, like all quantum simulations, is a mapping-a translation. The fidelity of the translation is relevant, but the true test will be whether the resulting ‘text’ reveals something new about the original language. The system learns to age gracefully; the art lies in learning to read the wrinkles.

Original article: https://arxiv.org/pdf/2602.04948.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-07 00:16