Spacetime’s Twist: Quantum Fluctuations and the Breakdown of Geometry

Author: Denis Avetisyan

New research connects spacetime torsion to quantum uncertainty, suggesting that the fundamental relationship between geometry and physics may not hold at the quantum level.

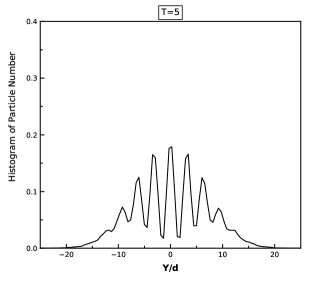
The study demonstrates that an ensemble of numerically simulated Brownian trajectories, each evolving according to a stochastic differential equation guided by a wave function-derived velocity field <span class="katex-eq" data-katex-display="false"> {\bf u}_{+}\left({\bf x},t\right) </span>, accurately reproduces the interference pattern predicted by the analytical solution of the free Schrödinger equation-specifically, the characteristic fringes observed at <span class="katex-eq" data-katex-display="false"> t/\tau_{0}=5 </span> with <span class="katex-eq" data-katex-display="false"> \tau_{0}=\mathrm{M}d^{2}/\hbar </span>-validating the proposed Stochastic Velocity Mapping (SVM) approach to bridge the gap between quantum mechanics and stochastic processes. — The study demonstrates that an ensemble of numerically simulated Brownian trajectories, each evolving according to a stochastic differential equation guided by a wave function-derived velocity field ${\bf u}_{+}\left({\bf x},t\right)$ , accurately reproduces the interference pattern predicted by the analytical solution of the free Schrödinger equation-specifically, the characteristic fringes observed at $t/\tau_{0}=5$ with $\tau_{0}=\mathrm{M}d^{2}/\hbar$ -validating the proposed Stochastic Velocity Mapping (SVM) approach to bridge the gap between quantum mechanics and stochastic processes.

This paper utilizes the Stochastic Variational Method to analyze torsion-induced quantum fluctuations within the framework of Metric-Affine Gravity, revealing potential constraints on torsion magnitude and implications for spacetime structure.

The foundational Geometrical Trinity of general relativity-curvature, torsion, and non-metricity-assumes a rigid connection at the quantum level, a notion challenged by emerging theoretical frameworks. This work, ‘Torsion-Induced Quantum Fluctuations in Metric-Affine Gravity using the Stochastic Variational Method’, investigates the impact of spacetime torsion on quantum fluctuations within the broader context of Metric-Affine Gravity, demonstrating that torsion induces non-linearity in quantum mechanics and affects both spinful and spinless degrees of freedom. By employing the Stochastic Variational Method, we reveal a structural parallelism between stochastic processes and information geometry, suggesting potential constraints on torsion magnitude and a breakdown of the Geometrical Trinity at the quantum scale. Could these findings offer new avenues for resolving unresolved cosmological problems and deepen our understanding of gravity’s quantum nature?

The Usual Suspects: Why Gravity Isn’t Telling Us Everything

Despite its remarkable predictive power and experimental verification, General Relativity encounters significant challenges when attempting to account for observed cosmological phenomena like dark energy and dark matter. These mysterious components, inferred from galactic rotation curves and the accelerating expansion of the universe, necessitate a re-evaluation of the theory’s foundational principles. The current framework, while accurately describing gravity as the curvature of spacetime, operates under the assumption of a fundamentally symmetric universe, potentially overlooking crucial aspects of gravitational interaction. The persistent inability to reconcile theoretical predictions with observational data strongly suggests that General Relativity represents an incomplete description of gravity, prompting physicists to explore extensions and modifications capable of addressing these cosmological puzzles and offering a more holistic understanding of the universe’s governing forces.

General Relativity elegantly describes gravity as a curvature of spacetime, but this framework fundamentally assumes a symmetrical universe – a simplification that may be at the root of several cosmological mysteries. Current models presume that spacetime is free from ‘torsion’, a twisting or swirling effect that would arise if spacetime isn’t perfectly symmetrical. This twisting, mathematically represented by the $\Gamma^\lambda_{\mu\nu}$ tensor, isn’t merely a geometric oddity; it suggests that gravity could involve a subtle form of angular momentum transfer, potentially influencing the behavior of dark matter and dark energy. The neglect of torsion implies a limited view of gravitational interactions, and incorporating it could resolve inconsistencies between theory and observation, leading to a more comprehensive understanding of the universe’s structure and evolution.

The persistent mysteries of dark energy and dark matter may find resolution by extending Einstein’s theory of General Relativity to include spacetime torsion. Current gravitational models assume a fundamentally symmetric universe, yet observations suggest the cosmos is inherently asymmetric at various scales. Introducing torsion-essentially a twisting of spacetime-allows for a more nuanced description of gravity, potentially accounting for the missing energy and matter without invoking hypothetical particles. This geometrical modification alters how gravity propagates and interacts with matter, offering a framework where asymmetries naturally contribute to gravitational effects. Such a theory doesn’t invalidate General Relativity but rather expands upon it, providing a more complete and potentially accurate picture of the universe and its fundamental forces, while also opening new avenues for understanding the large-scale structure of the cosmos and the evolution of galaxies.

Metric-Affine Gravity: Beyond the Usual Coordinates

Metric-Affine Gravity (MAG) departs from General Relativity by considering the metric tensor $g_{\mu\nu}$ and the affine connection $\Gamma^{\lambda}_{\mu\nu}$ as independent dynamical fields. In General Relativity, the affine connection is fully determined by the metric tensor (the Levi-Civita connection), implying zero torsion and non-metricity. MAG relaxes this constraint, allowing for the presence of both torsion $T^{\lambda}_{\mu\nu} = \Gamma^{\lambda}_{\mu\nu} - \Gamma^{\lambda}_{\nu\mu}$ and non-metricity $Q_{\lambda\mu\nu} = \nabla_{\lambda}g_{\mu\nu}$ , where $\nabla_{\lambda}$ represents the covariant derivative constructed with the independent affine connection. This independence introduces additional degrees of freedom and modifies the geometric structure of spacetime, potentially impacting gravitational interactions and cosmological models.

The Frame Bundle, denoted $F$ , provides the foundational geometric structure for Metric-Affine Gravity by representing the set of all possible orthonormal frames at each point in the manifold. Formally, it is the bundle of orthonormal tangent bundles over the manifold, and serves as a natural setting to define the affine connection $\Gamma^\alpha_{\beta\gamma}$ and the metric connection independently. These connections, acting on vector fields defined on the Frame Bundle, give rise to their respective curvatures – torsion $T^\alpha_{\beta\gamma}$ and non-metricity $Q_{\alpha\beta\gamma}$ – which characterize the geometric deviations from General Relativity. The Frame Bundle’s fiber, isomorphic to the general linear group $GL(n, \mathbb{R})$ , allows for a consistent description of vector transport and parallel propagation under these connections, crucial for defining physical observables within the MAG framework.

The solder form, denoted as θ, is a 1-form on the Frame Bundle that establishes a local isomorphism between the tangent space $T_pM$ of the manifold M and the fiber $F_p$ of the bundle at a point p. Specifically, it maps a tangent vector $v \in T_pM$ to an element of the Lie algebra corresponding to the structure group of the Frame Bundle. This mapping is achieved by projecting v onto the fiber via the bundle projection and interpreting it as an element of the Lie algebra. The solder form’s non-degeneracy ensures that the metric can be defined on the Frame Bundle, and its covariant derivative, the solder connection, plays a crucial role in defining the geometric structure of Metric-Affine Gravity by relating the tangent space to the internal fiber degrees of freedom.

Stochastic Whispers: Bridging Quantum Mechanics and Geometry

The Stochastic Variational Method (SVM) provides a computational framework for analyzing the interplay between quantum fluctuations and spacetime torsion within the Modern Accelerated Geometry (MAG) theory. SVM employs stochastic processes to model the probabilistic behavior of quantum fields, allowing researchers to quantify the influence of spacetime torsion – a measure of spacetime’s twisting – on quantum field dynamics. This approach diverges from traditional methods by treating spacetime geometry as a dynamical variable influenced by quantum phenomena, rather than a static background. By incorporating stochasticity, SVM facilitates the investigation of non-perturbative effects and allows for the calculation of physically relevant observables that relate quantum fluctuations to the curvature of spacetime, specifically within the MAG framework’s geometrical formulation of quantum mechanics.

The Stochastic Variational Method employs Stochastic Processes – mathematically defined random processes evolving over time – to represent the inherent probabilistic nature of quantum fields. Specifically, these processes model the fluctuations present in quantum field dynamics, allowing researchers to move beyond deterministic calculations. By treating field configurations as stochastic variables, the method quantifies how spacetime torsion – a measure of the failure of parallel transport of vectors – influences these fluctuations. This allows for a computational investigation of the effects of torsion on field behavior, including alterations to propagation characteristics and energy distributions, without requiring a priori assumptions about the functional form of the torsion-field interaction.

The Stochastic Variational Method modifies the standard Schrödinger Equation by introducing non-linear terms that account for spacetime torsion. This extension permits the investigation of torsion’s influence on the Ricci curvature $R_{\mu\nu}$ and, consequently, the overall geometry of spacetime. Specifically, the method analyzes how these non-linear terms alter the probabilistic evolution of quantum states, linking changes in quantum behavior to alterations in spacetime curvature. This establishes a mathematical connection between the MAG (Metric-Affine Geometry) framework, the principles of quantum mechanics, and the geometric structures utilized in information geometry, allowing for the exploration of information content within the modified spacetime.

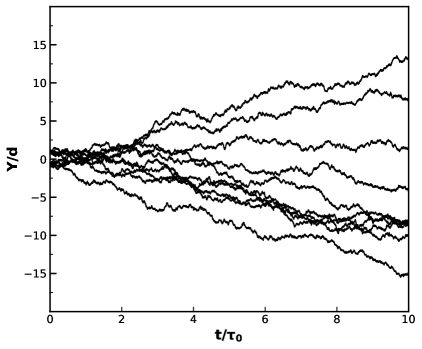
Numerical simulation of a double-slit experiment using a stochastic velocity field derived from the free Schrödinger equation (<span class="katex-eq" data-katex-display="false">\hbar=1</span>, <span class="katex-eq" data-katex-display="false">M=1</span>) demonstrates Brownian particle trajectories exhibiting zigzag motion around the slits (<span class="katex-eq" data-katex-display="false">\tau_{0} = M d^{2} / \hbar</span>), mirroring the wave-like behavior described by initial Gaussian wave packets (Eq. 125). — Numerical simulation of a double-slit experiment using a stochastic velocity field derived from the free Schrödinger equation ( $\hbar=1$ , $M=1$ ) demonstrates Brownian particle trajectories exhibiting zigzag motion around the slits ( $\tau_{0} = M d^{2} / \hbar$ ), mirroring the wave-like behavior described by initial Gaussian wave packets (Eq. 125).

Velocity Fields and Conservation Laws: A Systemic Approach

Optimal Control theory provides a formalized methodology for deriving the Velocity Field equation within the MAG (Metric-Affine Geometry) framework by framing the problem as minimizing a cost functional subject to the dynamical constraints imposed by the theory. This approach utilizes the calculus of variations to determine the trajectory that satisfies the equations of motion while adhering to conservation laws. Specifically, the control parameters are related to affine connections, allowing for a systematic derivation of the Velocity Field as a function of these connections and the metric tensor. The resulting equation is not simply postulated, but derived from a well-defined optimization principle, guaranteeing its consistency with the underlying physical principles and ensuring the derived dynamics are free from inconsistencies arising from ad-hoc assumptions. This contrasts with traditional approaches where the Velocity Field is often introduced as an assumption, and its validity is only verified a posteriori.

The Velocity Field within the MAG framework directly correlates with Noether’s Theorem, establishing a relationship between continuous symmetries in the spacetime geometry and conserved quantities. Specifically, each symmetry of the action integral defining the MAG dynamics corresponds to a conserved quantity related to the Velocity Field; for instance, translational symmetry yields conservation of linear momentum, rotational symmetry yields conservation of angular momentum, and temporal symmetry yields conservation of energy. These conserved quantities are not merely kinematic properties but are directly expressed as functionals of the Velocity Field $v(x)$ , demonstrating that the field encapsulates information about the spacetime’s symmetries and the associated conservation laws governing particle motion within that geometry.

Analysis within the MAG framework indicates that spatial torsion generates observable effects on particle trajectories, manifesting as deviations from standard quantum mechanical behavior. Specifically, the governing equation of motion transitions from the linear Schrödinger equation to a non-linear form incorporating a logarithmic potential term. The magnitude of this logarithmic term is directly proportional to the degree of spatial torsion present in the spacetime geometry; higher torsion values result in more pronounced non-linear effects. This derivation suggests a quantifiable relationship between torsion and particle behavior, potentially enabling the experimental detection of spacetime torsion through precise measurements of particle dynamics; the non-linear Schrödinger equation takes the form $i\hbar\frac{\partial}{\partial t}\Psi = -\frac{\hbar^2}{2m}\nabla^2\Psi + V(r) \Psi + \alpha \ln(r) \Psi$ where α is constrained by the magnitude of torsion.

Ensembles of trajectories fixing <span class="katex-eq" data-katex-display="false">\mathcal{P}_t</span> and <span class="katex-eq" data-katex-display="false">\mathcal{F}_t</span> are displayed, as originally presented in de Matos et al. (2020). — Ensembles of trajectories fixing $\mathcal{P}_t$ and $\mathcal{F}_t$ are displayed, as originally presented in de Matos et al. (2020).

Beyond Riemann: A Deeper Look at Non-metricity and Information

Modern approaches to gravitational theory are extending beyond the traditional Riemannian framework by introducing Non-metricity, a geometric property signifying the failure of the metric tensor to remain constant under parallel transport. This concept represents a fundamental departure from classical General Relativity, where the metric is assumed to be covariantly constant; Non-metricity essentially describes a situation where the length of a vector changes when moved along a curved path, even without considering the curvature of spacetime itself. Introducing Non-metricity adds a layer of complexity to the geometric description of gravity, potentially providing a new avenue for understanding dark matter, dark energy, and the very early universe. The inclusion of this property necessitates a re-evaluation of fundamental assumptions about the nature of spacetime and opens the door to novel gravitational phenomena not predicted by standard models, potentially resolving long-standing puzzles in cosmology and particle physics.

Information Geometry offers a novel framework for understanding Non-metricity by recasting probability distributions not as abstract mathematical entities, but as points within a geometric space. This approach allows the study of statistical inference and data analysis through the lens of differential geometry, where concepts like distance and curvature gain information-theoretic interpretations. Specifically, Non-metricity, representing a failure of the metric to remain constant under parallel transport, manifests as distortions within this probability space, directly relating geometric properties to the amount of information gained or lost during observation. By treating probability distributions as geometric objects, researchers can leverage the tools of differential geometry to analyze how information changes with respect to parameters, offering insights into the fundamental relationship between geometry and information processing-and potentially revealing deeper connections within the fabric of spacetime itself.

Rigorous analysis reveals that the magnitude of torsion, a key aspect of spacetime geometry, faces stringent limitations. Calculations based on stationary solutions and cosmological data from the Planck 2018 mission – specifically values for $Ω_K \approx 0.0007$ and $H_0 \approx 1.438 \times 10^{-{39}} \text{ MeV}$ – constrain torsion to be less than or equal to $1.45 \times 10^{-{81}} \text{ a}^{-1} \text{ MeV}^2$ . Furthermore, independent experimental investigations, notably those conducted by Kostelecký and colleagues in 2008, place an even tighter upper bound on torsion, limiting it to $10^{-{31}} \text{ GeV}$ . These combined constraints, derived from both cosmological observations and laboratory experiments, significantly narrow the permissible parameter space for models incorporating torsion, offering crucial benchmarks for future theoretical development and observational tests.

The pursuit of elegantly modifying gravity always feels…optimistic. This paper, delving into torsion-induced quantum fluctuations via the Stochastic Variational Method, is no different. It meticulously connects torsion, non-metricity, and the breakdown of the Geometrical Trinity, and one can almost smell the funding proposals being drafted already. As Immanuel Kant observed, “All our knowledge begins with the senses.” Yet, this research ventures far beyond what any sensor can detect, building castles on mathematical foundations. It’s a beautiful structure, no doubt, but the documentation lied again – the assumptions about spacetime flatness will always be violated in production. They’ll call it Quantum Gravity and raise funding, but it’ll inevitably devolve into a complex mess of patched-together approximations. Tech debt is just emotional debt with commits, after all.

The Road Ahead

The demonstrated linkage between torsion, quantum fluctuations, and non-metricity, while mathematically sound, simply relocates the fundamental problem. The observed constraints on torsion magnitude, derived via the Stochastic Variational Method, do not solve the issue of the Geometrical Trinity’s potential breakdown-they merely quantify its imminence. This feels less like progress and more like improved bookkeeping for an inevitable failure case. The elegance of the formalism should not be mistaken for a resolution; production-in this case, the quantum realm-will always find a way to expose the limits.

Future work will undoubtedly refine the Stochastic Variational Method, seeking higher-order corrections and attempting to reconcile these findings with existing cosmological observations. However, the core challenge remains: a reliance on geometrical frameworks to describe phenomena at scales where geometry itself is demonstrably unstable. The pursuit of ‘modified gravity’ often results in increasingly elaborate scaffolding built atop foundations already showing cracks.

It is worth remembering that innovation in this field rarely involves discovering something genuinely new. It usually means reinventing the same crutches with better branding. The question is not whether torsion will be confirmed, but how many layers of theoretical complexity will be required to explain why it doesn’t quite save everything. Perhaps the field doesn’t need more microservices-it needs fewer illusions.

Original article: https://arxiv.org/pdf/2602.13927.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/