Author: Denis Avetisyan
New research leverages hypernuclear physics and Bayesian inference to refine our understanding of the forces governing ultra-dense matter inside neutron stars.
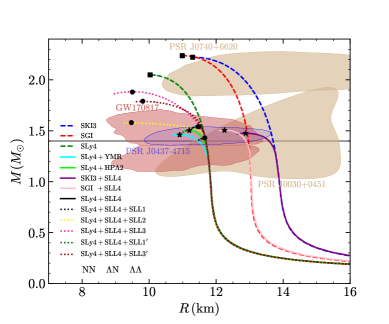
This study constrains the neutron star equation of state by investigating the role of three-body hyperon forces in both multi-Λ hypernuclei and the interiors of massive neutron stars.
The poorly constrained nature of hyperon interactions presents a significant challenge in modeling the behavior of ultra-dense matter found in neutron star interiors. This study, ‘Exploring Hyperon Skyrme Forces in Multi-Λ Hypernuclei and Neutron Star Matter’, employs a Bayesian analysis within the Skyrme Hartree-Fock framework to investigate two- and three-body forces between hyperons and nucleons, constrained by both hypernuclear data and astrophysical observations. Results demonstrate that incorporating three-body hyperon forces notably stiffens the equation of state, allowing for neutron stars up to 22% more massive, and reconciling theoretical models with observed \sim 2\,M_{\odot} neutron stars. How will continued refinement of these interactions further illuminate the fundamental properties of matter at extreme densities and compositions?
Unveiling the Secrets of Ultra-Dense Matter
Neutron stars represent an extreme state of matter, born from the gravitational collapse of massive stars and packing the mass of the sun into a sphere roughly the size of a city. This incredible density – exceeding that of an atomic nucleus – subjects matter to conditions unattainable in any terrestrial laboratory, pushing the boundaries of established physics. At these densities, the very fabric of spacetime is warped, and the fundamental interactions governing matter are drastically altered. Consequently, neutron stars serve as unique cosmic laboratories for testing theories of gravity and the strong nuclear force, offering crucial insights into the behavior of matter under the most extreme conditions imaginable. The study of these stellar remnants isn’t merely an exercise in astrophysics; it’s a probe into the fundamental nature of reality itself, challenging existing models and potentially revealing new physics.
Predicting the behavior of neutron stars demands a precise understanding of their internal composition, which is fundamentally tied to the Equation of State (EquationOfState) – a mathematical description relating pressure, density, and temperature within the star. Constructing an accurate EquationOfState for NeutronStarMatter presents a formidable challenge because the extreme densities – exceeding that of atomic nuclei – force matter into an uncharted territory where the conventional laws of physics are pushed to their limits. Theoretical models must account for interactions between neutrons, protons, and potentially more exotic particles, all while aligning with observational constraints gleaned from gravitational wave detections and electromagnetic observations. The difficulty arises not only from the complexity of these interactions, but also from the inherent uncertainties in extrapolating known physics to such extreme conditions, making the EquationOfState a key focus of ongoing research and a crucial stepping stone towards unraveling the mysteries of these cosmic enigmas.
Despite decades of research, current theoretical models of neutron star interiors fail to consistently align with observational data, creating what is known as the ‘HyperonPuzzle’. These models, designed to predict the behavior of matter at extreme densities, often overestimate the stiffness of neutron star matter when incorporating the expected presence of hyperons – exotic particles containing strange quarks. This discrepancy leads to predicted neutron star radii that are significantly larger than those inferred from X-ray observations of these celestial objects. The puzzle isn’t simply a matter of refining existing calculations; it suggests a potential gap in understanding the fundamental interactions between these particles at such extreme pressures, potentially requiring revisions to the underlying theories of nuclear physics or the consideration of previously unknown phenomena within neutron star cores. Resolving this inconsistency is critical, as it directly impacts the ability to accurately determine the Equation of State of NeutronStarMatter and, ultimately, to understand the behavior of matter under the most extreme conditions in the universe.
The extreme density within neutron stars necessitates the consideration of exotic particles beyond the familiar protons and neutrons. Hyperons, baryons containing strange quarks, are theorized to appear at these densities, fundamentally altering the star’s Equation of State – the relationship between pressure and density. However, incorporating hyperons into models presents substantial challenges. Their interactions with other particles are poorly constrained due to limited experimental data, and accurately predicting these interactions requires complex many-body calculations. Furthermore, the inclusion of hyperons can lead to a ‘softer’ Equation of State, potentially resolving discrepancies between theory and observation, but also raising the ‘HyperonPuzzle’ – the question of why these particles haven’t been more readily detected in observational data given their predicted abundance. Consequently, refining hyperon interaction models remains a critical frontier in understanding the behavior of matter at its densest form and accurately characterizing neutron star properties.
Modeling Strong Interactions: The Skyrme Force Approach
The Skyrme force is a density-dependent, non-relativistic effective interaction used to describe the strong nuclear force between nucleons. It provides a computationally tractable approach to modeling nuclear matter, relying on a two-body interaction term and density-dependent terms to account for many-body effects. This force, expressed mathematically as a sum of two-body interactions and three-body terms, allows for the calculation of the energy per nucleon in nuclear matter as a function of density. By adjusting the parameters within the Skyrme force, such as the effective mass and incompressibility, researchers can simulate the behavior of nuclear systems under extreme conditions, like those found in neutron stars or heavy-ion collisions. The success of the Skyrme force lies in its ability to reproduce key properties of finite nuclei and infinite nuclear matter with a relatively small number of parameters, making it a foundational tool in nuclear physics and astrophysics.
The Skyrme force, a non-relativistic effective theory of nuclear forces, requires parameterization to define specific interactions between nucleons. The SLy4 parameter set is frequently employed as a foundational model for calculations of nuclear matter properties due to its well-defined functional form and reasonably accurate reproduction of ground-state nuclear characteristics. This parameterization defines the strength and range of the effective nucleon-nucleon interaction, directly influencing the predicted Equation of State (EOS) of nuclear matter. By establishing a baseline EOS with SLy4, subsequent modifications and extensions-such as incorporating hyperons-can be assessed for their impact on the overall behavior of dense baryonic matter. The SLy4 parameter set provides a consistent framework for evaluating the contributions of various interaction terms to the total energy density and pressure of the system, ultimately informing our understanding of neutron stars and other high-density astrophysical objects.
Accurate modeling of hyperonic interactions requires modifications to the standard Skyrme force due to the unique characteristics of hyperons within nuclear matter. The SLL4 parameterization is specifically designed to address \Lambda N interactions, which differ from nucleon-nucleon interactions due to the weaker coupling of the Λ baryon. Standard Skyrme forces, like SLy4, do not adequately describe these interactions, leading to inaccuracies in the calculated Equation of State at densities where hyperons become relevant. SLL4 incorporates adjustments to the potential to better reflect the observed properties and scattering cross-sections of Λ nucleons, thereby improving the fidelity of dense matter simulations.
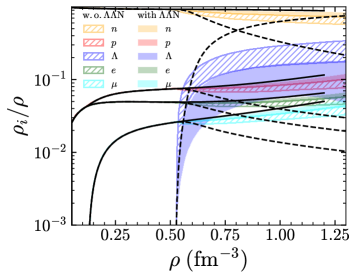
The Equation of State (EOS) in dense matter calculations is sensitive to more than just the strength of the nuclear force; the EffectiveMass of baryons, which is modified by interactions, plays a crucial role in determining macroscopic properties. Calculations employing the SLy4+SLL4 interaction parameter set, designed to model hyperonic interactions, indicate that hyperons begin to appear in nuclear matter at a density of 0.86 fm⁻³. This threshold density is directly influenced by the baryon EffectiveMass, highlighting the necessity of accurately accounting for interaction-induced mass modifications when constructing realistic EOS models for neutron stars and other dense astrophysical objects.
Constraining the Model: Evidence from Experiment and Inference
Hypernuclear experiments directly investigate the strong force interactions between hyperons – baryons containing strange quarks – and nucleons within the environment of an atomic nucleus. These experiments typically involve producing hypernuclei through the replacement of a nucleon with a hyperon, then observing the resulting energy shifts or decay patterns. Analysis of these observables, such as single-particle energies and lifetimes, provides quantitative constraints on the hyperon-nucleon and hyperon-hyperon interaction potentials. The experimental data is crucial because it offers an independent validation of theoretical models, which often rely on extrapolations from nucleon-nucleon scattering or chiral effective field theory, and allows for refinement of the Equation of State used to model neutron stars.
Hypernuclear experiments and multi-messenger astronomy observations provide independent, yet complementary, constraints on theoretical models describing dense matter. Hypernuclear data, derived from studying nuclei containing hyperons, directly probes the strong interaction between hyperons and nucleons within a nuclear environment. Multi-messenger astronomy, particularly observations of neutron star mergers via gravitational waves and electromagnetic radiation, offers insights into the equation of state of matter at extreme densities, exceeding those achievable in terrestrial laboratories. By comparing predictions from theoretical models – such as those describing hyperonic interactions – with the results of these experiments and observations, researchers can assess the validity of those models and refine their parameters. Discrepancies between model predictions and observational data indicate areas where the theoretical understanding of dense matter requires improvement, driving further research and model development.
Bayesian inference provides a statistical framework for updating parameters defining hyperonic interactions. This process integrates data from hypernuclear experiments – which directly measure hyperon-nucleon and hyperon-hyperon interactions – with prior theoretical constraints. By applying Bayes’ theorem, the method calculates a posterior probability distribution for each parameter, representing the likelihood of different parameter values given the observed evidence. This allows for a systematic refinement of interaction models, quantifying uncertainties, and improving the predictive capability of the Equation of State used to describe dense matter in neutron stars and other extreme astrophysical environments. The method effectively combines experimental observations with theoretical predictions, providing a robust approach to constraining the properties of hyperonic matter.
Bayesian inference techniques are utilized to assess the probability of various hyperonic interaction models when confronted with observational data, thereby refining the Equation of State (EoS) and improving its predictive capabilities. Analysis employing the SLy4+SLL4 EoS indicates the potential existence of hyperon stars with a calculated maximum mass of 2.03 – 0.03 + 0.01 solar masses (M_{\odot}). At this maximum mass, the corresponding stellar radius is determined to be 9.82 – 0.16 + 0.17 kilometers, representing a constrained parameter space for hyperon star characteristics based on current data and modeling.
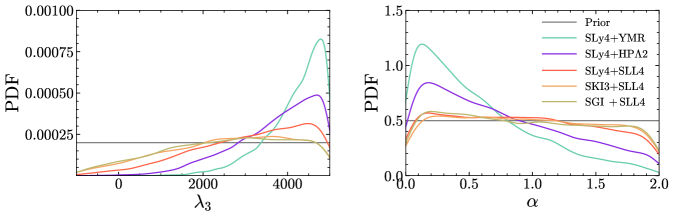
Implications for Neutron Star Physics and Beyond
Predicting the properties of neutron stars-their mass, radius, and how easily they deform under gravitational forces (tidal deformability)-hinges critically on a precise understanding of the matter within them, particularly the interactions between hyperons. These exotic particles, heavier cousins of protons and neutrons, are theorized to appear at the incredibly high densities found in neutron star cores. An accurate Equation of State, which describes the relationship between pressure and density, must incorporate the complex, many-body interactions between these hyperons to avoid discrepancies between theoretical models and observational data from gravitational wave detectors and X-ray telescopes. Without this precision, estimations of neutron star parameters remain uncertain, hindering the ability to probe the fundamental physics governing matter under the most extreme conditions in the universe and potentially masking the presence of even more exotic forms of matter.
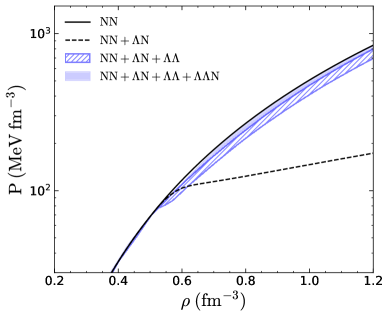
Accurate descriptions of nuclear matter at saturation density, and especially at the extreme densities found within neutron stars, require more than just pairwise interactions between nucleons. Three-body forces – interactions involving three nucleons simultaneously – represent a crucial component for a complete understanding, as they account for many-body effects not captured by simpler two-body potentials. Current models often struggle to reconcile theoretical predictions with observational constraints on neutron star properties, and discrepancies are frequently traced to an incomplete treatment of these three-body interactions. These forces subtly alter the energy landscape of dense nuclear matter, influencing the stability of hyperonic matter and impacting quantities like the equation of state, maximum neutron star mass, and tidal deformability. Ignoring or improperly modeling these effects can lead to significant errors in predicting the behavior of matter under such extreme conditions, hindering efforts to unlock the mysteries of these fascinating celestial objects.
The persistent “Hyperon Puzzle” extends far beyond neutron star interiors, touching upon fundamental symmetries governing matter at extreme densities. Current theoretical frameworks predict that hyperons – baryons containing strange quarks – should appear in the cores of massive neutron stars, softening the equation of state and limiting maximum masses. However, observations of stars exceeding these predicted limits necessitate a reevaluation of hyperon interactions and their impact on stellar structure. Resolving this discrepancy isn’t merely an astrophysical refinement; it probes the validity of Quantum Chromodynamics (QCD) under conditions unattainable in terrestrial experiments. Specifically, understanding how hyperons interact with each other and with nucleons tests the underlying symmetries of strong interactions and potentially reveals subtle violations, providing crucial insights into the nature of quark confinement and the emergence of hadronic matter. Ultimately, unraveling the Hyperon Puzzle could illuminate the behavior of matter at any extreme density, from the cores of neutron stars to the early universe, and potentially unveil previously unknown states of matter.
Investigations into neutron star mergers stand to reveal the crucial role hyperons play under the extreme pressures and densities present during these cataclysmic events. Recent analysis, utilizing the SLy4+SLL4 interaction, suggests a central density of 1.26 - 0.03 + 0.04 fm⁻³ at the maximum mass of a neutron star, providing a more precise constraint on the behavior of matter at these scales. Furthermore, this work narrows the range of possible values for the \Lambda\Lambda interaction parameter \lambda_0, indicating a predominantly attractive force between these particles. These findings not only refine current models of neutron star structure but also open the possibility of discovering novel, exotic states of matter – potentially including hyperonic matter or even more unconventional phases – that emerge under the immense pressures generated during neutron star mergers, pushing the boundaries of known physics.
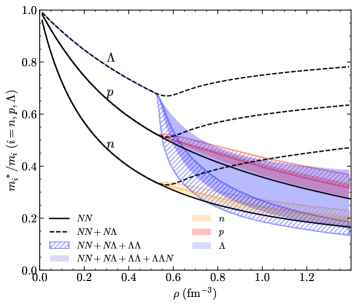
The investigation into hyperon interactions within multi-Λ hypernuclei and neutron star matter exemplifies a systematic approach to understanding complex systems. Just as Immanuel Kant stated, “Begin with the question: what may I know?” this study rigorously explores the limits of current knowledge regarding the equation of state of dense matter. By employing Skyrme forces and Bayesian inference, researchers dissect the contributions of three-body hyperon forces, revealing their significant role in supporting the existence of massive neutron stars. This methodical process-isolating variables, testing hypotheses, and refining understanding-mirrors the Kantian pursuit of knowledge through reason and observation, ultimately revealing the underlying patterns governing these extreme astrophysical phenomena.
The Road Ahead
The exploration of hyperon interactions, as presented, reveals a curious pattern: the necessity of three-body forces to reconcile theoretical models with observed neutron star masses. Yet, this reliance itself becomes a new challenge. Each parameter constrained within the Skyrme force framework simultaneously defines a multitude of others, creating a complex web of interdependence. The question isn’t merely whether these forces exist, but whether the chosen formalism adequately captures their underlying physics, or simply provides a convenient, albeit effective, parametrization.
Future investigations must move beyond simply fitting equations of state to data. A deeper exploration of the density-dependent behavior of these three-body terms is crucial. Are there emergent phenomena at play within the hypernuclear many-body system, subtly influencing the overall pressure and stability? Furthermore, the direct connection between laboratory hypernuclear experiments and the extreme conditions within neutron stars remains tenuous. Improved experimental probes, capable of accessing higher densities and momentum transfer, are essential to validate theoretical predictions.
Ultimately, this work highlights a familiar truth: every image – be it a hypernuclear spectrum or a neutron star observation – is a challenge to understanding, not just a model input. The search for the equation of state isn’t a quest for a single number, but an ongoing refinement of the patterns that govern matter at its most extreme.
Original article: https://arxiv.org/pdf/2602.03388.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- Ashes of Creation Rogue Guide for Beginners
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 28 Years Ago Today, The Simpsons Sparked Controversy With a 10/10 Episode Banned in Some Regions
- Travis Kelce Reveals He & Fiancée Taylor Swift Never Argue
- Which Stranger Things Character Are You, Based On Your Zodiac Sign?
2026-02-04 13:24