Taming Quantum Chaos with Magnetic Fields

Author: Denis Avetisyan

---

New research demonstrates how transverse magnetic fields can be used to control the scrambling of quantum information in chaotic systems.

This study reveals a connection between guiding-center motion in magnetic fields and the suppression of quantum chaos, utilizing out-of-time-order correlators to characterize scrambling dynamics.

The interplay between quantum chaos and external control remains a central challenge in understanding thermalization. This is addressed in ‘More on OTOCs and Chaos in Quantum Mechanics — Magnetic Fields’, which revisits thermal out-of-time-order correlators (OTOCs) in single-particle quantum systems subject to magnetic fields. Our analysis of stadium billiards reveals tunable control over scrambling dynamics, demonstrating a crossover from quantum chaos to magnetic rigidity and a distinct suppression of exponential growth when employing guiding-center coordinates. How do these findings inform our broader understanding of scrambling and the emergence of effective thermalization in increasingly complex quantum systems?

---

The Whispers of Disorder: Quantum Chaos and Initial Conditions

The shift from the predictable realm of quantum mechanics to the seemingly random behavior of classical physics isn’t abrupt, but a gradual transition characterized by what scientists call quantum chaos. Investigating this transition demands more than simply observing a system; it requires tools capable of quantifying the degree to which quantum states become disordered and unpredictable. Traditional methods, often successful with simple systems, falter when confronted with the complexity of many-body quantum systems where interactions scramble information in ways that defy classical intuition. Characterizing this ‘quantumness’ of chaos involves measuring how sensitive a quantum system is to initial conditions – a concept echoing the ‘butterfly effect’ of classical chaos – but adapted for the unique rules governing the quantum world. Ultimately, understanding quantum chaos isn’t just about observing disorder; it’s about developing the theoretical and experimental tools to precisely measure and map the boundary between quantum and classical behavior.

Characterizing the behavior of complex quantum systems presents a significant challenge because traditional analytical methods, designed for simpler scenarios, often fail to adequately capture the rapid and intricate scrambling of quantum information. This scrambling, where information about a quantum state spreads throughout the system, isn’t a simple diffusion but a fundamentally different process governed by the principles of quantum mechanics. Consequently, metrics used to describe classical chaos – such as Lyapunov exponents – become ineffective, providing little insight into the dynamics of these systems. The difficulty arises from the exponential growth of the Hilbert space with increasing system size, making it computationally intractable to track the evolution of information using conventional techniques. This limitation underscores the need for novel approaches capable of directly quantifying the rate and nature of this quantum scrambling, paving the way for a deeper understanding of the transition from quantum to classical behavior.

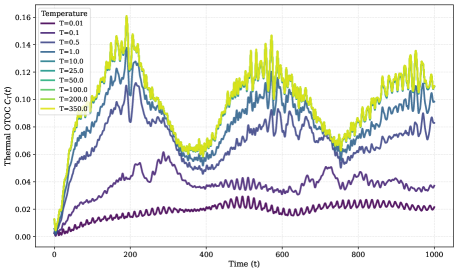
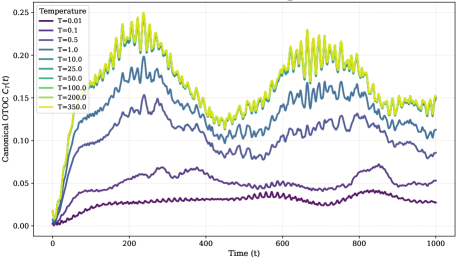
Characterizing the scrambling of quantum information, a hallmark of quantum chaos, demands a shift in measurement techniques beyond traditional correlation functions. Instead, investigations now focus on out-of-time-ordered correlations – quantities that reveal how information about an initial state is dispersed and becomes inaccessible over time. These correlations don’t measure whether two observables commute now, but rather whether they would have commuted if measured at different points in time, effectively probing the system’s memory of its past states. Measuring these correlations, often expressed as D(t) = \frac{1}{N} \sum_{i,j} \langle z_i(t) z_j(0) \rangle^2 , allows researchers to quantify the rate at which information spreads within a quantum system and provides a sensitive indicator of the transition from regular quantum behavior to the chaotic regimes seen in larger, more complex systems. This approach offers a powerful pathway to understand how quantum systems lose coherence and ultimately approach classicality.

Unveiling the Scrambling: Computational Tools for Quantum Chaos

The approach outlined by Hashimoto et al. establishes a key framework for calculating the Out-of-Time-ordered Correlation function (OTOC) within single-particle quantum systems. This formalism centers on expressing the OTOC as a time-ordered product of operators, which allows for its evaluation using Keldysh formalism and non-perturbative techniques. Specifically, the method relies on representing the time evolution operator as a path integral and employing a series expansion in terms of the interaction strength. This allows the OTOC to be related to the system’s Green’s functions, facilitating its computation and providing a means to quantify the rate of quantum chaos in these systems. The technique’s utility stems from its ability to move beyond perturbative approximations, offering insights into strongly-correlated single-particle dynamics.

The Hashimoto formalism for computing the Out-of-Time-ordered Correlation function (OTOC) relies on a specific structure of the underlying Hamiltonian. Introduction of external forces, notably magnetic fields, disrupts this structure by modifying the system’s dynamics and introducing non-trivial commutation relations. Specifically, the presence of a magnetic field leads to the quantization of electron orbits into Landau levels, altering the energy spectrum and necessitating modifications to the computational approach. The standard implementation of the formalism, designed for free particle systems, no longer directly applies due to the altered phase space and the increased complexity of evaluating the necessary commutators and time-evolved operators. This requires a reformulation of the calculations to account for the modified dynamics and the discrete energy levels arising from the external field.

The application of the Hashimoto formalism for Out-of-Time-Ordered Correlation (OTOC) calculations becomes complex in systems subject to external forces, specifically magnetic fields. These forces induce quantization of electron motion into discrete energy levels known as Landau levels. The energy separation between these levels, proportional to the magnetic field strength, fundamentally alters the system’s dynamics and spectral properties. Consequently, accurately computing OTOCs requires incorporating the discrete Landau level structure into the calculation, necessitating a modification of the original formalism to account for this quantization and its impact on the system’s response functions. Failure to do so will result in inaccurate predictions of the system’s chaotic behavior and quantum information scrambling properties, as the continuous energy spectrum assumption underpinning the initial formalism is no longer valid.

Mapping the Trajectory: Guiding Center Coordinates and OTOC Construction

Guiding center coordinates provide a means of simplifying the analysis of charged particle motion within magnetic fields by focusing on the trajectory of the particle’s guiding center – the average position around which the particle gyrates. Rather than directly tracking the particle’s position subject to the Lorentz force, this coordinate system effectively decouples the fast cyclotron motion from the slower drift motion induced by spatial gradients in the magnetic field \mathbf{B} and any external forces. Specifically, the coordinates describe the motion of the guiding center as if the particle experienced a reduced effective force, allowing for a clearer determination of particle trajectories and facilitating calculations of quantities like drift velocity and magnetization. This approach is particularly useful when the Larmor radius is small compared to the scale length of the magnetic field variations, enabling treatment of the cyclotron motion as an internal degree of freedom.

The Guiding Center Operator-valued Time-ordered product of observables (OTOC) is constructed using guiding center coordinates to simplify the analysis of charged particle dynamics in magnetic fields. Traditional OTOC calculations become significantly more complex due to the rapid oscillations associated with cyclotron motion; utilizing guiding center coordinates effectively averages over these high-frequency terms. This simplification allows for a clearer identification of the contributions from the slower, drift-scale dynamics, and facilitates the calculation of quantities such as the thermalization rate and quantum scrambling. The resulting Guiding Center OTOC directly reflects the semiclassical behavior of the guiding center and provides a more tractable framework for examining the system’s response to perturbations and external potentials.

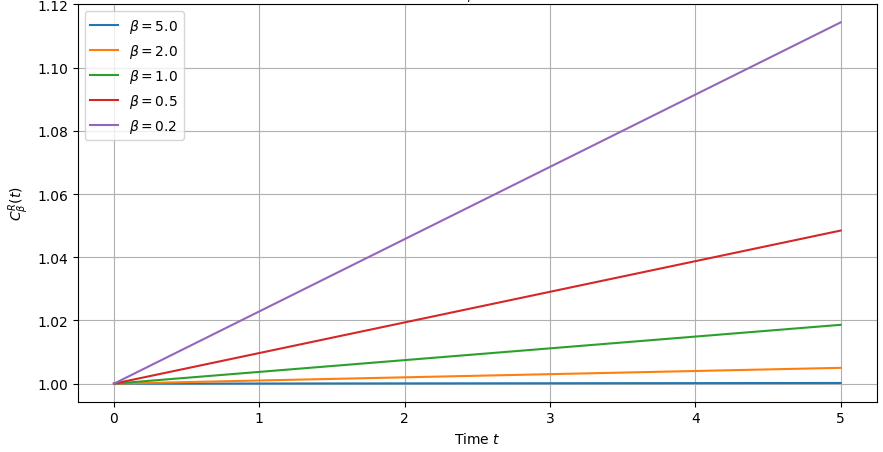
Analysis utilizing guiding center coordinates and the resulting Out-of-Time-Order Correlator (OTOC) exhibits a linear-in-time thermal growth rate, indicative of the effective semiclassical dynamics governing the guiding centers within a non-uniform potential. This linear growth stems from the adiabatic invariance of the magnetic moment, μ, which constrains the guiding center motion and prevents rapid scrambling. The observed rate directly corresponds to the drift velocity of the guiding centers in the potential gradient, providing a quantifiable measure of their dynamics and validating the semiclassical approximation in this context. Consequently, the OTOC serves as a diagnostic tool for characterizing the effective dynamics of charged particles subject to both magnetic and potential forces.

The Echo of Chaos: Lyapunov Exponents and the Limits of Prediction

Out-of-Time-Ordered Correlators (OTOCs) provide a powerful means of quantifying the sensitivity of a quantum system to initial conditions, ultimately revealing the rate at which infinitesimally close trajectories diverge – a value known as the Lyapunov exponent. This exponent doesn’t merely indicate the presence of chaos, but precisely measures its intensity; a larger Lyapunov exponent signifies a more rapid separation of trajectories and, consequently, a faster scrambling of information within the system. Essentially, it captures how quickly a tiny perturbation grows, transforming a nearly identical starting point into a dramatically different future state, and is therefore a defining characteristic of chaotic dynamics. The ability to extract this exponent from OTOCs offers a direct window into the underlying chaotic behavior, allowing researchers to characterize and compare the sensitivity of various quantum systems.

The presence of a positive Lyapunov exponent serves as a definitive signature of chaotic behavior within a dynamical system. This exponent doesn’t merely indicate chaos, but crucially, quantifies the rate at which nearby trajectories diverge – a measure of sensitivity to initial conditions. More intuitively, it describes how rapidly information about a small perturbation spreads throughout the system. A larger positive exponent signifies a faster scrambling of information, implying a more vigorous and efficient exploration of the system’s available states. This capability is not simply a mathematical curiosity; it has implications for understanding the limits of predictability and the fundamental mechanisms governing complex systems, from fluid turbulence to the behavior of quantum particles. The exponent, therefore, provides a powerful tool for characterizing and comparing the degree of chaos in diverse physical phenomena.

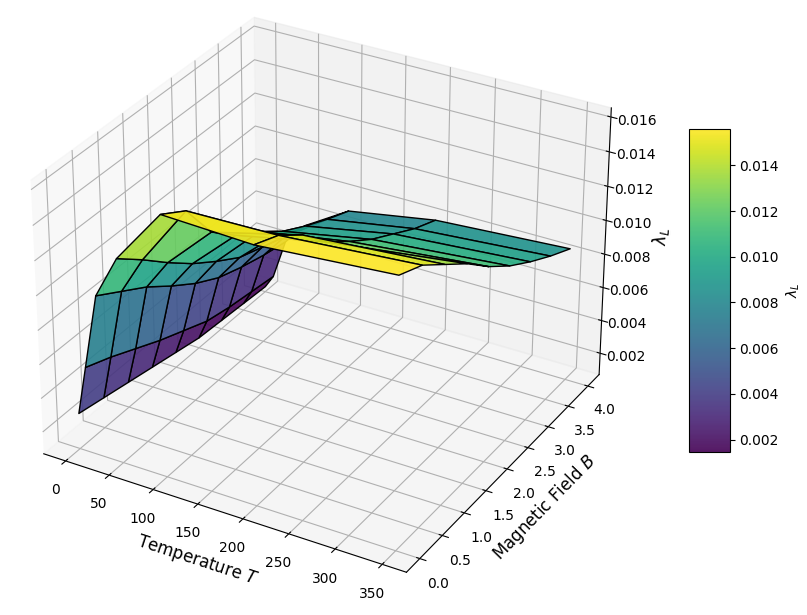
Recent research into quantum billiards-systems modeling particle behavior within confined spaces-reveals a fascinating control over quantum chaos through the application of transverse magnetic fields. These fields don’t simply suppress chaotic behavior; they orchestrate a delicate interplay between the natural chaos arising from the billiard’s boundaries and the confining influence of the magnetic force. This modulation is quantified by a newly identified Lyapunov-like exponent, which specifically measures the rate at which quantum information spreads-or “scrambles”-within the system during its initial evolution. The findings demonstrate that the strength of the magnetic field directly influences this scrambling rate, effectively tuning the degree of quantum chaos and offering insights into the fundamental dynamics of information dispersal in complex quantum systems.

The degree of chaotic behavior within the quantum billiard system is not static, but rather demonstrably sensitive to external conditions. Calculations reveal that the Lyapunov exponent-a key indicator of the rate at which trajectories diverge-fluctuates in response to both temperature and the strength of the applied magnetic field. At lower magnetic field strengths, the system exhibits robust chaotic growth, signified by a substantial positive Lyapunov exponent. However, as the magnetic field increases, this chaotic behavior is progressively suppressed; the Lyapunov exponent diminishes, indicating a transition towards more ordered dynamics. This tunability suggests a compelling interplay between boundary-induced chaos and the confining influence of the magnetic field, offering a mechanism to control the rate of information scrambling within the quantum system.

The study meticulously details how magnetic fields introduce a degree of order within the chaotic dynamics of quantum billiards, effectively tuning the scrambling of quantum information. This control over chaos, achieved through external parameters, echoes a sentiment articulated long ago by Epicurus: “It is not the pursuit of pleasure itself that is wrong, but the excessive pursuit of it.” Similarly, this research demonstrates that while chaos is a fundamental aspect of quantum systems, it isn’t an absolute; a measured application of magnetic fields, a form of ‘control’, can temper its intensity. The exploration of Lyapunov exponents and out-of-time-order correlators reveals a delicate balance, a reminder that even within seemingly random systems, underlying order-or a controllable degree of order-can be found.

Where Do We Go From Here?

This exploration of magnetic fields and quantum chaos, predictably, opens more questions than it closes. The demonstrated control over scrambling dynamics is not, of course, control in any meaningful sense. It is merely a shifting of parameters, a refined ability to lose track of things with greater precision. The connection between guiding-center motion and suppressed chaos is interesting, but it feels suspiciously like finding order in the inevitable drift toward entropy – a comforting illusion.

Future work will undoubtedly refine the tuning of these magnetic fields, perhaps seeking some elusive ‘sweet spot’ where chaos is not extinguished, but managed. This seems a futile endeavor. Black holes are the best teachers of humility; they show that not everything is controllable. The real challenge lies not in suppressing chaos, but in understanding the fundamental limits of predictability, even in systems as seemingly simple as a billiard table.

Theory is a convenient tool for beautifully getting lost. Perhaps the next step isn’t more precise calculations, but a deeper acceptance of the inherent unknowability of complex systems. The pursuit of order, after all, may be less about finding it, and more about enjoying the exquisite patterns that emerge from the void.

---

Original article: https://arxiv.org/pdf/2602.05322.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

• Best Controller Settings for ARC Raiders

• Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled

• 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)

• DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]

• Ashes of Creation Rogue Guide for Beginners

• Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!

• 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)

• 10 Most Brutal Acts Of Revenge In Marvel Comics History

• One Piece’s Anime Hit With Another Surprising Delay

• Star Trek 4’s Development Hell Just Got So Much Worse

2026-02-06 22:34