The Fabric of Reality: Scaling Laws and Quantum Spacetime

Author: Denis Avetisyan

A new theoretical framework proposes that spacetime isn’t fundamental, but emerges from the dynamics of scale measurements and quantum fluctuations.

Microscopic spacetime fluctuations exhibit directional dependence determined by the sign of <span class="katex-eq" data-katex-display="false">\bar{X}^{\alpha}_{0}</span>; when <span class="katex-eq" data-katex-display="false">\bar{X}^{\alpha}_{0}</span> is negative, fluctuations occur with a characteristic length scale defined by <span class="katex-eq" data-katex-display="false">\bar{X}^{\alpha}_{0}/2 < L_{-} \leq \bar{X}^{\alpha}_{0}</span> and <span class="katex-eq" data-katex-display="false">L_{+} \geq \bar{X}^{\alpha}_{0}</span>, reversing for positive values of <span class="katex-eq" data-katex-display="false">\bar{X}^{\alpha}_{0}</span>. — Microscopic spacetime fluctuations exhibit directional dependence determined by the sign of $\bar{X}^{\alpha}_{0}$ ; when $\bar{X}^{\alpha}_{0}$ is negative, fluctuations occur with a characteristic length scale defined by $\bar{X}^{\alpha}_{0}/2 < L_{-} \leq \bar{X}^{\alpha}_{0}$ and $L_{+} \geq \bar{X}^{\alpha}_{0}$ , reversing for positive values of $\bar{X}^{\alpha}_{0}$ .

This review details a scaling-based quantization approach to spacetime microstructure, exploring its connection to generalized uncertainty principles and discrete spacetime geometries.

The persistent challenge of reconciling general relativity with quantum mechanics necessitates novel approaches to understanding spacetime at the Planck scale. This is addressed in ‘Scaling-Based Quantization of Spacetime Microstructure’, which proposes a framework where spacetime geometry emerges from the dynamics of local scale factors rather than the metric itself. By formulating a scale-based quantization procedure utilizing a hierarchy of scale manifolds, the work demonstrates the emergence of spacetime discreteness and quantizes fluctuations as harmonic oscillators, yielding a microscopic description of zero-point energy. Could this approach offer a pathway towards resolving the cosmological constant problem and a consistent theory of quantum gravity?

Unveiling the Quantum Fabric: Spacetime’s Hidden Fluctuations

Contemporary physics largely relies on a depiction of spacetime as a smooth, continuous fabric, a concept that has proven remarkably successful in describing gravitational phenomena at observable scales. However, this model may be an approximation, obscuring a far more complex reality at the Planck scale – the smallest unit of length with physical meaning. At this level, quantum effects are predicted to induce significant fluctuations in the geometry of spacetime itself, potentially rendering the very notions of distance and time probabilistic rather than deterministic. These aren’t merely minor distortions; theoretical calculations suggest spacetime could be bubbling with quantum foam, a chaotic landscape of virtual black holes and wormholes constantly appearing and disappearing. Investigating these hypothesized fluctuations is crucial, as they represent a potential breakdown of general relativity and a gateway to a more complete understanding of gravity at its most fundamental level – a realm where the smooth spacetime continuum gives way to a granular, fluctuating quantum geometry.

If spacetime is indeed subject to fluctuations at the Planck scale, the very foundations of geometrical understanding require revision. Concepts traditionally considered absolute – distance, area, and volume – would become inherently uncertain, losing their fixed values and instead manifesting as probabilistic distributions. Consequently, the measurement of energy, intimately linked to spacetime through $E=mc^2$ , would also be affected, potentially leading to violations of energy conservation at extremely small scales. This isn’t merely a technical refinement; it suggests that the universe, at its most fundamental level, operates under principles drastically different from those currently described by general relativity and quantum field theory, demanding a new mathematical language to accurately represent reality and potentially resolving inconsistencies between these two pillars of modern physics.

The persistent challenges at the intersection of quantum mechanics and general relativity – notably the singularities within black holes and the initial conditions of the universe – may find resolution through a deeper understanding of spacetime fluctuations. Current theoretical frameworks struggle to reconcile the probabilistic nature of quantum phenomena with the deterministic geometry of gravity, leading to mathematical inconsistencies and physically unrealistic predictions. However, by incorporating the inherent ‘fuzziness’ of spacetime at the Planck scale – a scale where quantum effects dominate – physicists propose a pathway towards a consistent theory of quantum gravity. Such a framework doesn’t merely address technical difficulties; it fundamentally alters the landscape of cosmology, potentially offering explanations for dark energy, the origin of cosmic inflation, and the very nature of spacetime itself, moving beyond the classical picture of a smooth, continuous fabric to a dynamic, fluctuating entity.

To account for the inherent distortions predicted by spacetime fluctuations, a novel theoretical construct utilizing ‘Scale Factors’ has been developed. These factors, mathematically represented as localized deviations from unity, effectively model the minute stretching and compressing of spacetime at the Planck scale. Rather than treating spacetime as a rigid backdrop, this framework allows for a dynamic, probabilistic geometry where distances and durations are not absolute but are subject to these fluctuating scale factors. $\delta S$ represents the magnitude of these fluctuations, influencing calculations of energy density and gravitational interactions. By incorporating these scale factors into existing models, researchers aim to move beyond the limitations of classical general relativity and explore a more nuanced understanding of quantum gravity, potentially resolving inconsistencies between quantum mechanics and cosmology.

A Geometric Foundation: Mapping the Fluctuations

The proposed First-Order Manifold serves as the foundational geometric structure for modeling spacetime. This manifold is not a static entity; it incorporates locally varying ‘Scale Factors’ – dimensionless quantities denoted as $\lambda(x)$ – which represent deviations from a flat, undistorted spacetime. These scale factors are functions of spacetime coordinates $x$ and directly influence the metric tensor, effectively describing localized distortions in the geometry. The inclusion of these scale factors allows for a dynamic representation of spacetime, where the metric is not fixed but rather fluctuates based on the distribution of these localized distortions. This approach provides a geometric framework for investigating phenomena arising from spacetime irregularities.

The Scaled Metric is a fundamental component of the First-Order Manifold, serving to quantify both distances and curvatures within the modeled spacetime. Unlike a static metric which assumes fixed geometric properties, the Scaled Metric is dynamically adjusted by the Scale Factors, thereby accommodating local distortions. This means that the distance $dl$ between two infinitesimally close points is not simply determined by a constant tensor $g_{\mu\nu}$ , but by a tensor modified by these scale factors: $dl^2 = g_{\mu\nu}(x) \, dx^\mu dx^\nu + \text{scale factor corrections}$ . Consequently, curvature, as described by the Riemann curvature tensor, is also a fluctuating quantity dependent on the distribution of these Scale Factors, directly reflecting the dynamic and potentially inhomogeneous nature of spacetime as proposed by the model.

The Second-Order Manifold provides a geometric representation of the scale factor amplitudes generated by the First-Order Manifold. This manifold is not a spatial dimension, but rather a space defined by the possible values and rates of change of these scale factors – effectively, a parameter space describing the fluctuations in spacetime distortion. Each point on the Second-Order Manifold corresponds to a specific configuration of scale factor amplitudes across the First-Order Manifold. Its dimensionality is determined by the number of independent scale factors required to fully describe the spacetime distortions within the primary geometry; thus, it allows for the analysis of the dynamics of the scaling itself, rather than simply the scaled geometry. $\mathcal{M}_2$ is used to denote the Second-Order Manifold.

The Scaling Lagrangian, denoted as $L = L_0 + L_s$ , provides the dynamical description of the First- and Second-Order Manifolds. $L_0$ represents the Lagrangian for the base First-Order Manifold, governing its geometric evolution. $L_s$ is the Lagrangian for the scale factors, defined on the Second-Order Manifold, and incorporates terms representing the kinetic and potential energies associated with fluctuations in these scale factors. Specifically, $L_s$ is constructed to ensure the stability of the system and to model the interactions between spacetime distortions at different locations, thereby establishing a self-consistent framework for describing the dynamic behavior of the combined geometric structure.

The curves demonstrate that <span class="katex-eq" data-katex-display="false">\beta(L^{\alpha}(X^{\alpha}))</span> scales proportionally with <span class="katex-eq" data-katex-display="false">L^{\alpha}(X^{\alpha})</span> and <span class="katex-eq" data-katex-display="false">X^{\alpha}</span> when <span class="katex-eq" data-katex-display="false">\bar{X}^{\alpha}_{0}=0</span> and <span class="katex-eq" data-katex-display="false">|\bar{X}^{\alpha}_{0}|=1.6</span>. — The curves demonstrate that $\beta(L^{\alpha}(X^{\alpha}))$ scales proportionally with $L^{\alpha}(X^{\alpha})$ and $X^{\alpha}$ when $\bar{X}^{\alpha}_{0}=0$ and $|\bar{X}^{\alpha}_{0}|=1.6$ .

Dynamical Consequences: Reshaping the Equations of Reality

The Scaling Lagrangian introduces modifications to the standard model by incorporating scale factors that directly influence the definition of spacetime curvature. Specifically, the $Riemann \, Curvature \, Tensor$ and the $Christoffel \, Symbols$ – fundamental components in describing the geometry of spacetime – are altered through these scale factors. This modification implies that the gravitational interaction, as described by general relativity, is no longer fixed but becomes a dynamic quantity dependent on these scaling parameters. Consequently, the very fabric of spacetime is redefined, potentially leading to variations in gravitational effects and affecting the propagation of particles and light. These alterations necessitate a re-evaluation of established gravitational phenomena and introduce the possibility of scale-dependent gravitational constants.

Modifications to the $Klein-Gordon Equation$ and the $Dirac Equation$ are achieved through the introduction of scale factors, directly impacting the propagation of relativistic particles. These scale factors, denoted as $A(x)$ , are incorporated as multiplicative terms within the equations’ derivatives, effectively altering the spacetime metric experienced by the particles. Specifically, the standard derivative $\partial_{\mu}$ is replaced with $A(x)\partial_{\mu}$ , causing a rescaling of momentum and energy. This modification results in altered particle dispersion relations and modifies the predicted probabilities of particle interactions, potentially leading to observable deviations from standard model predictions and affecting phenomena such as vacuum decay rates and particle tunneling probabilities.

Adaptations to the $Geodesic Equations$ are necessary when considering spacetime subject to fluctuations introduced by scaling factors. Traditionally, these equations describe the paths of objects moving under the influence of gravity, assuming a static spacetime metric. However, with fluctuating spacetime, the metric becomes time-dependent, requiring modifications to the $Geodesic Equations$ to accurately predict trajectories. These modifications involve incorporating the time derivatives of the metric tensor into the equations, effectively accounting for the changing geometry of spacetime. Consequently, the paths of objects are no longer strictly geodesics in a static sense but rather curves influenced by the dynamic spacetime, leading to deviations from Newtonian or general relativistic predictions in scenarios with significant spacetime fluctuations.

Modal decomposition, when applied to fields influenced by scale factors, yields a quantization of field modes. This process decomposes the field into individual modes, each characterized by an eigenvalue $ω_i^2 = k_i/m_i$ . Here, $ω_i$ represents the frequency of the i-th mode, $k_i$ denotes a mode-specific constant related to the scale factor, and $m_i$ is a mass parameter associated with that mode. The eigenvalues directly determine the stability of the vacuum state; positive eigenvalues indicate stability, while negative eigenvalues suggest vacuum decay. Analysis of these quantized modes and their corresponding eigenvalues provides insight into the dynamic behavior of the spacetime fabric and its influence on relativistic fields.

Quantum Implications: Unveiling the Microscopic Structure

The conventional calculation of zero-point energy, a fundamental concept in quantum field theory, relies on an assumption of flat spacetime. However, this framework proposes that spacetime geometry is not static, but rather dynamically influenced by scale factor fluctuations at the Planck scale. This altered geometry significantly impacts the determination of zero-point energy, as the energy density associated with vacuum fluctuations is intimately linked to the volume of spacetime. Consequently, the standard formulas require modification to account for these fluctuations, leading to a revised estimate of the minimum energy state of the universe. The implications extend beyond theoretical considerations, potentially influencing cosmological models and our understanding of dark energy, as the effective cosmological constant is directly related to the calculated zero-point energy density. The framework, therefore, presents a novel approach to resolving the long-standing discrepancy between theoretical predictions and observed values of vacuum energy.

At the Planck scale, the very fabric of spacetime exhibits fluctuations, necessitating a revised approach to defining area. Researchers constructed a ‘Microscopic Area Operator’ to account for these quantum distortions, moving beyond a classical geometrical interpretation. This operator doesn’t simply measure area; it inherently incorporates the probabilistic nature of scale factor fluctuations – minute, yet significant, variations in the dimensions of space itself. By treating area as an operator, rather than a fixed value, the framework allows for a more accurate description of how area manifests at extremely small scales, effectively blurring the line between geometry and quantum mechanics. The resulting formulation is crucial for connecting the microscopic description of spacetime with macroscopic thermodynamic properties, such as the entropy of black holes, and is mathematically represented through considerations of $a_{iso}$ , the isotropic scale factor.

A significant outcome of this theoretical framework is its ability to replicate the $Bekenstein-Hawking$ entropy – the measure of a black hole’s disorder – directly from microscopic principles. By connecting the area of the event horizon to the statistical behavior of fundamental degrees of freedom, the calculations yield the established area law $S_{BH} = A/(4l_p^2)$ , where $A$ represents the horizon area and $l_p$ is the Planck length. This correspondence isn’t merely a mathematical coincidence; it suggests a deep connection between gravity, thermodynamics, and the quantum structure of spacetime, indicating that black hole entropy arises from the underlying microscopic area and its associated quantum states. The successful reproduction of this well-known result lends strong support to the validity of the approach and its potential to illuminate the quantum nature of gravity and black holes.

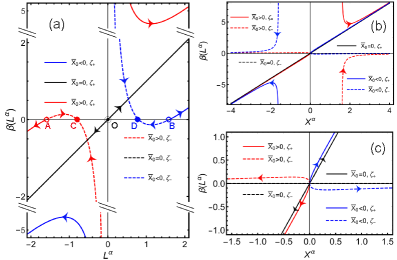
The behavior of this framework is fundamentally dictated by a ‘Scaling Renormalization Group’, which governs how scale factors change under magnification or reduction-essentially, how the system responds to changes in observation scale. This group’s action dictates the overall dynamics, leading to specific eigenvalues that characterize the scaling behavior in different directions. In a Euclidean space, the parallel eigenvalue is calculated as $λ∥ = D-1 a_{iso}^4$ , while the perpendicular eigenvalue is $λ⊥ = 3(D-1) a_{iso}^4$ , where ‘D’ represents the dimensionality of the space and $a_{iso}$ is an isotropic scale factor. These eigenvalues are not merely mathematical curiosities; they reveal how the system’s properties-like energy and entropy-transform as the scale of observation changes, ultimately connecting microscopic fluctuations to macroscopic thermodynamic laws.

Future Directions: Probing the Quantum Realm

The ‘Micro-Measurement’ framework establishes a novel theoretical approach to investigate the fundamental structure of spacetime at the incredibly small Planck scale. This methodology doesn’t rely on directly observing Planck-scale phenomena, which is currently beyond experimental capabilities, but instead utilizes mathematically defined scale functions to effectively ‘measure’ the fluctuations inherent in spacetime itself. By analyzing how these scale functions behave and interact, physicists can indirectly probe the quantum geometry of spacetime, revealing information about its granular structure and potential deviations from the smooth, continuous model described by classical general relativity. This allows researchers to move beyond traditional limitations and explore the very fabric of reality using purely theoretical tools, opening avenues for understanding quantum gravity and the nature of spacetime at its most fundamental level – where distances are approximately $1.6 \times 10^{-{35}}$ meters.

Detecting the subtle tremors of spacetime itself presents a significant challenge for future investigations, requiring innovative experimental approaches to verify predictions stemming from theoretical frameworks like the ‘Micro-Measurement’ approach. Researchers are actively exploring potential signatures of spacetime fluctuations – distortions at the Planck scale – through various avenues, including precision measurements of light propagation, searching for violations of Lorentz invariance, and analyzing the cosmic microwave background for non-Gaussianities. These investigations aim to identify minute deviations from established physical laws that could betray the quantum nature of spacetime, potentially revealing its granular structure. Successful detection would not only confirm the existence of these fluctuations but also offer a unique window into the fundamental nature of gravity and the very fabric of reality, possibly linking these effects to phenomena such as dark energy and the accelerating expansion of the universe.

Investigating the quantum properties of scale factors necessitates treating them not as classical parameters, but as quantum operators residing within a ‘Fock Space’. This approach, borrowed from quantum field theory, allows researchers to analyze the scale factors as excitations of a quantum system, revealing their possible energy levels and statistical behavior. By applying the mathematical tools of Fock Space, such as creation and annihilation operators, it becomes possible to explore the potential for quantum fluctuations in spacetime itself. This formalism could unveil whether the expansion and contraction of the universe, typically described by continuous scale factors, are fundamentally discrete or probabilistic at the Planck scale, potentially resolving inconsistencies between general relativity and quantum mechanics. Furthermore, analyzing these quantized scale factors within a Fock Space framework may provide a pathway to understanding the very nature of spacetime geometry and its implications for cosmology.

The framework’s potential extends to unraveling the mysteries of dark energy and the accelerating expansion of the universe, suggesting a connection between spacetime fluctuations and these cosmological phenomena. Analysis of Minkowski spacetime within this model reveals specific eigenvalues – $\lambda_{time} = -(D-1) a_{iso}^4$ , $\lambda_{space}(\parallel) = D-1 a_{iso}^4$ , and $\lambda_{space}(\perp) = 3(D-1) a_{iso}^4$ – which represent characteristic scales of quantum fluctuations in time and space. These eigenvalues, dependent on the isotropic scale factor $a_{iso}$ and the dimensionality $D$ of spacetime, offer a potential pathway to understanding the energy density driving cosmic acceleration and may provide a crucial link between quantum gravity and large-scale cosmological observations, potentially refining current models of dark energy.

The exploration within this work emphasizes the fundamental role of scale in defining spacetime geometry. It posits that observing the universe necessitates understanding its inherent granularity, a concept beautifully echoed by Werner Heisenberg: “The ultimate values of the constants of nature are not determined by the laws of nature, but by the structure of the universe.” This notion aligns with the paper’s investigation into scale manifolds and how fluctuations within these manifolds give rise to the observed spacetime. Rigorous examination of these scaling degrees of freedom, as detailed in the approach to a Scaling Lagrangian, requires careful attention to data boundaries to avoid spurious patterns and accurately represent the underlying discrete structure of spacetime.

Where to Next?

The proposition that spacetime geometry arises from the dynamics of scale measurements offers a compelling, if unconventional, path forward. However, the current framework, while mathematically consistent, remains largely disconnected from readily observable phenomena. Establishing a demonstrable link between these scaling degrees of freedom and experimentally verifiable predictions presents the most immediate challenge. Further refinement of the microscopic area operator, and its subsequent implications for the Generalized Uncertainty Principle, are crucial. The theory’s predictive power, particularly concerning deviations from Lorentz invariance at Planck scales, demands rigorous scrutiny.

A significant limitation lies in the absence of a fully developed dynamical model. The scaling Lagrangian, while providing a foundational structure, requires extension to incorporate matter fields and their interactions. Exploring the consequences of this extension – the emergence of gravity as an effective field theory, the resolution of singularities in black holes, or the potential for pre-Big Bang cosmology – will necessitate considerable effort. Moreover, the framework’s compatibility with established quantum field theory needs careful investigation.

Ultimately, the validity of any approach to quantum gravity rests not on mathematical elegance, but on empirical confirmation. If a pattern cannot be reproduced or explained, it doesn’t exist. The true test of this scaling-based quantization will be its ability to predict novel phenomena, or to resolve long-standing paradoxes, in a manner consistent with observation.

Original article: https://arxiv.org/pdf/2601.15649.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/