Author: Denis Avetisyan
New research explores the consequences of a fundamentally ‘fuzzy’ space-time, potentially resolving conflicts between quantum mechanics and our understanding of the universe’s origins.
This review examines the implications of Snyder space-a noncommutative geometric framework-for statistical thermodynamics and early universe cosmology, including observable effects in Big Bang Nucleosynthesis.
The standard framework of quantum gravity often struggles to reconcile the principles of general relativity and quantum mechanics, prompting exploration of modified spacetime geometries. This is the focus of ‘Statistical physics on Euclidean Snyder space: connections with the GUP and cosmological implications’, which investigates the consequences of a momentum-space curvature-encoded in Euclidean Snyder space-on statistical mechanics and early-universe cosmology. The authors demonstrate that this curvature induces temperature-dependent corrections suppressing thermodynamic quantities and, crucially, provides a pathway to constrain noncommutative geometry via observations of Big Bang Nucleosynthesis. Could precision cosmological probes, therefore, offer a unique window into the fundamental nature of spacetime at the Planck scale?
Beyond Conventional Spacetime: Introducing Snyder Space
The prevailing models of cosmology, such as the Lambda-CDM model, have achieved remarkable success in describing the evolution and large-scale structure of the universe. However, these models ultimately rely on a marriage between general relativity, which governs gravity and spacetime, and quantum mechanics, which dictates the behavior of matter at the smallest scales. This union remains deeply problematic; attempts to combine the two consistently lead to mathematical inconsistencies and physically nonsensical predictions, particularly when probing extreme conditions like the very early universe or within black holes. These difficulties suggest that our fundamental understanding of spacetime itself may be incomplete, prompting physicists to explore modifications to the smooth, continuous fabric described by general relativity. The persistent inability to reconcile these foundational theories strongly indicates that a more nuanced, potentially discrete, structure underlies the cosmos, necessitating a re-evaluation of spacetime as a fundamental entity.
The persistent challenge of unifying quantum mechanics and general relativity has motivated exploration beyond the conventional understanding of spacetime as a smooth continuum. Noncommutative geometry offers a powerful mathematical language to describe scenarios where the coordinates of space do not commute – meaning the order in which measurements are taken matters – effectively introducing a fundamental granularity to spacetime itself. Within this framework, Snyder space stands out as a particularly compelling model; it postulates that spacetime coordinates \hat{x}^\mu and \hat{y}^\nu satisfy a commutation relation of the form [\hat{x}^\mu, \hat{y}^\nu] = i \theta^{\mu\nu}, where θ represents a deformation parameter. This noncommutativity leads to a momentum-space curvature and, crucially, can act as a natural ultraviolet cutoff for quantum gravity, potentially resolving the problematic singularities that plague current theories and offering a pathway toward a more complete description of the universe at its most fundamental level.
Snyder space posits a radical departure from traditional spacetime, fundamentally altering the way coordinates are understood; instead of simply representing points, these coordinates do not commute – meaning the order in which they are multiplied matters. This noncommutativity introduces a natural granularity to spacetime, effectively ‘blurring’ distances at the Planck scale. Crucially, this isn’t a modification of coordinate labels, but a property of the spacetime geometry itself, manifesting as a curvature within momentum space – a reciprocal relationship to the usual position-space curvature described by general relativity. The consequence of this momentum-space curvature is twofold: it potentially eliminates the singularities that plague black holes and the Big Bang, offering a mathematically consistent description of these extreme environments, and it provides a natural ultraviolet (UV) cutoff for gravity – a mechanism to tame the infinities that arise when attempting to combine quantum mechanics and general relativity. In essence, Snyder space suggests that spacetime isn’t infinitely divisible, but rather composed of discrete ‘chunks’, offering a pathway towards a more complete and consistent theory of quantum gravity.
The Mathematical Architecture: Operators and Quantization
Snyder space is constructed using the SO(4) algebra, which provides the mathematical framework for defining the generators of its Cartesian coordinate operators. Specifically, the SO(4) Lie algebra’s generators, denoted J_i and K_i where i = 1, 2, 3, 4, are utilized to build these coordinate operators. These generators satisfy commutation relations defining the algebra, and through a non-commutative parameter, introduce a fundamental length scale. The Cartesian coordinate operators X_i are then defined as linear combinations of these generators, resulting in a non-commutative spacetime structure inherent to Snyder space. This construction ensures Lorentz invariance is preserved despite the non-commutativity, a key feature of the model.
The operators defining Snyder space, specifically those representing Cartesian coordinates, do not possess continuous eigenvalues; instead, their spectra are discrete. This discretization directly implies a fundamental granularity to spacetime itself, meaning that distances are not infinitely divisible but are limited by a minimum measurable length. Consequently, calculations reveal that area is also quantized, with permissible values existing only as multiples of a fundamental area unit \Delta A . This quantization arises from the non-commutativity of the coordinate operators and has implications for the measurement of geometric quantities at the Planck scale, effectively introducing a minimum area element.
The quantization of area in Snyder space directly implies the existence of a minimum observable length scale. This arises because area is constructed from powers of coordinate operators; discrete area spectra necessitate a lower bound on the eigenvalues of these operators, effectively preventing arbitrarily small distances. This concept extends the Generalized Uncertainty Principle (GUP), which modifies the Heisenberg uncertainty relation to include terms proportional to \Delta x^2 , leading to a minimum uncertainty in position. Consequently, the GUP, as manifested in Snyder space, provides a natural regularization mechanism in quantum field theory by effectively introducing a shortest distance cutoff, preventing divergences that typically arise from integrating over arbitrarily small distances and high energies. This regularization occurs without the need for artificial or ad hoc procedures.
Cosmological Echoes: From Expansion to Nucleosynthesis
Snyder space, a non-commutative spacetime geometry, introduces a length scale that modifies the Hubble expansion rate. Standard cosmological models rely on a constant Hubble parameter or slowly varying dark energy to explain the accelerating expansion of the universe; however, Snyder space provides an alternative mechanism through its inherent modification of spacetime at high energies. This modification effectively alters the relationship between redshift and distance, impacting calculations of the Hubble constant, H_0. The degree of modification is dependent on the Snyder momentum scale, a fundamental parameter characterizing the non-commutativity. Consequently, observations of the expansion rate, such as those from Type Ia supernovae and cosmic microwave background anisotropies, can be used to constrain the value of this scale, potentially offering a new avenue for understanding the accelerating expansion without invoking dark energy or requiring modifications to General Relativity at lower energies.
The application of Statistical Thermodynamics within the non-commutative geometry of Snyder space provides a theoretical framework for investigating the behavior of matter under extreme conditions, specifically those prevalent in the early universe. This approach utilizes the principles of statistical mechanics, but incorporates the modifications to momentum space inherent in Snyder space – where \hat{p}_i \hat{p}_j \rightarrow \hat{p}_i \hat{p}_j + i \theta_{ij} – to recalculate partition functions and thermodynamic properties. By treating the Snyder deformation as a high-energy effect, it becomes possible to model the equation of state and phase transitions of matter at energy scales inaccessible to conventional methods, offering insights into the conditions immediately following the Big Bang and potentially resolving discrepancies in models of early universe cosmology.
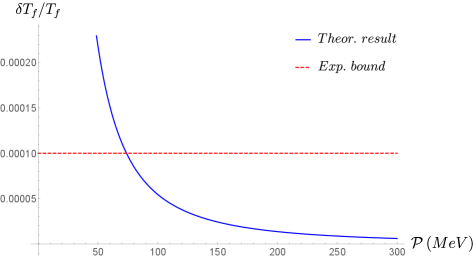
Big Bang Nucleosynthesis (BBN) calculations, which predict the primordial abundances of light elements like hydrogen, helium, and lithium, are affected by modifications to the early universe’s expansion rate and particle interactions introduced by Snyder space. Our analysis reveals a direct correlation between the predicted abundances and the Snyder Momentum Scale M_{S}. Specifically, to remain consistent with observational constraints derived from measurements of these light element abundances, the Snyder Momentum Scale must be greater than or equal to 102 MeV. Values of M_{S} below this threshold predict light element abundances that deviate significantly from established cosmological observations, effectively ruling out those lower scales within this theoretical framework.
Quantum Gravity’s Footprint: Freeze-Out and Beyond
The very early universe, a cauldron of extreme energies, witnessed the decoupling of fundamental particles as it expanded and cooled. This process, known as freeze-out, is deeply sensitive to the underlying physics governing particle interactions, and crucially, to the scale at which quantum gravity effects become significant. Recent investigations reveal that the Snyder momentum scale, a parameter characterizing the minimum observable momentum arising from theories of quantum gravity, directly impacts the freeze-out temperature – the point at which these weak interactions cease. A modified momentum scale alters the thermal velocities of particles, effectively changing the rate of interactions and thus the temperature at which they decouple. This has profound consequences for predicting the abundance of relic particles, such as dark matter, as the final number density is determined by the interaction rate at the moment of freeze-out. Consequently, precision measurements of the cosmic microwave background and Big Bang Nucleosynthesis can serve as powerful probes, not only of cosmological parameters but also of the fundamental structure of spacetime at the Planck scale, offering a novel pathway to indirectly detect quantum gravitational effects.
The subtle shifts in early universe physics, stemming from the Snyder Momentum Scale, have a direct impact on calculations of dark matter relic abundance. Standard dark matter predictions rely on precise freeze-out temperatures, representing the point where dark matter particle annihilation ceases due to the universe’s expansion; alterations to this temperature, as demonstrated by recent analysis, necessitate a reevaluation of these predictions. Consequently, the expected density of dark matter in the present-day universe shifts, potentially resolving discrepancies between theoretical models and observational data. More importantly, this opens a new window for indirect detection strategies, as the altered annihilation cross-sections and decay channels could manifest as unique signals in gamma-ray, cosmic-ray, and neutrino spectra, offering a novel pathway to confirm the nature of dark matter and distinguish it from other potential astrophysical sources.
Analysis of early universe freeze-out processes has yielded significantly refined constraints on the Generalized Uncertainty Principle (GUP), a theoretical framework suggesting a minimal length scale in nature. By relating the GUP parameter β = m_p^2 / 𝒫^2 to variations in the freeze-out temperature during Big Bang Nucleosynthesis (BBN), researchers have established a lower bound on the Snyder Momentum Scale of at least 102 MeV. This represents an improvement of several orders of magnitude over previous constraints derived from BBN alone, offering a more precise probe of quantum gravity effects at extremely high energies and bolstering the potential for indirect detection of dark matter candidates influenced by these modifications to spacetime.
The exploration of Snyder space, as detailed in the research, reveals a fascinating interplay between geometry and physics. It suggests that fundamental constants may not be absolute, but rather emerge from the underlying structure of spacetime. This echoes a sentiment expressed by Grigori Perelman, who once stated, “It is better to remain silent and be thought a fool than to speak and to remove all doubt.” Perelman’s remark, while seemingly unrelated, highlights the importance of rigorous thought and careful consideration of assumptions-a principle central to this study’s investigation of noncommutative geometry and its implications for cosmology. The suppressed thermodynamic quantities resulting from momentum-space curvature demonstrate that seemingly small alterations to foundational geometric principles can yield significant consequences for our understanding of the universe.
Beyond the Horizon
The exploration of Snyder space, as presented, yields a fascinating, if subtle, deformation of familiar statistical mechanical landscapes. The suppression of thermodynamic quantities, born from momentum-space curvature, is not merely an academic exercise. It hints at a deeper resonance between the abstract architecture of noncommutative geometry and the tangible realities of physical systems. The question, however, remains whether these effects are sufficiently pronounced to escape the noise of conventional physics, or if they are destined to remain whispers in a shouting universe.
A crucial avenue for future work lies in refining the connection to Big Bang Nucleosynthesis. While the preliminary indications are promising, a robust phenomenological analysis, accounting for the complex interplay of particle physics and cosmology, is essential. The current framework operates, necessarily, with a degree of simplification. Expanding it to incorporate more realistic models-and, crucially, rigorously quantifying the uncertainties-will be paramount.
Ultimately, the true elegance of this approach will be revealed not through mathematical complexity, but through predictive power. The current work proposes a framework; the next step demands its confrontation with observation. A minimal length scale, elegantly woven into the fabric of spacetime, is a compelling idea. Whether it leaves an imprint on the universe-a delicate trace for diligent observers to find-remains to be seen.
Original article: https://arxiv.org/pdf/2602.02506.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- Ashes of Creation Rogue Guide for Beginners
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 28 Years Ago Today, The Simpsons Sparked Controversy With a 10/10 Episode Banned in Some Regions
- Bitcoin’s Bullish Blunders: The $98,000 Soap Opera 🎭
- DC K.O.: Superman vs Captain Atom #1 Uses a Fight as Character Study (Review)
2026-02-04 08:20