The Ghost in the Standard Model: Tracking the Light Dilaton

Author: Denis Avetisyan

---

A new theoretical framework details the interactions of the dilaton, a potential particle arising from broken scale invariance, with known Standard Model particles.

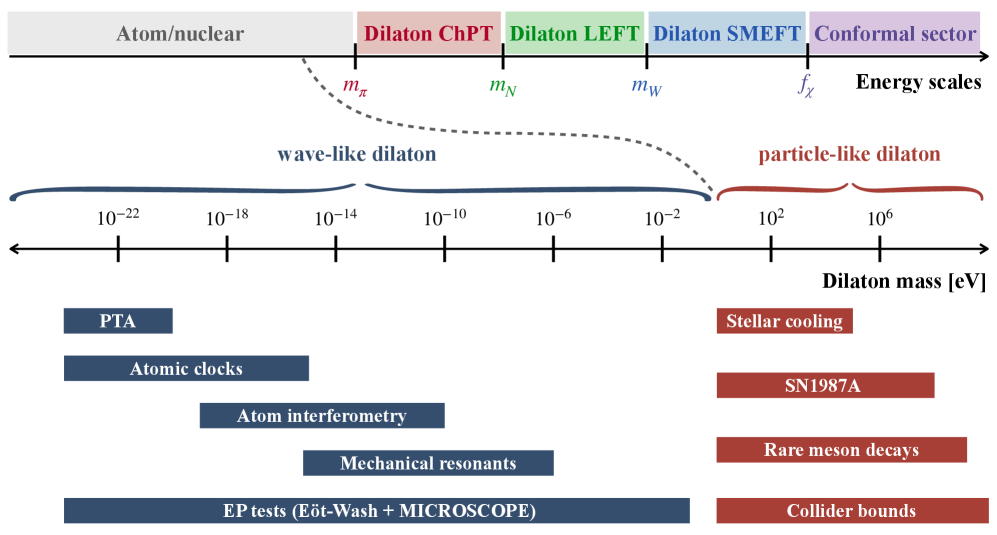
This review develops a comprehensive effective field theory for the light dilaton and explores constraints on its properties from experimental phenomenology.

While extensions to the Standard Model often invoke axion-like particles, a consistent low-energy framework for the dilaton-the pseudo-Nambu-Goldstone boson of spontaneously broken scale symmetry-has remained elusive. This paper, ‘Effective Field Theory Description of Light Dilaton’, constructs a systematic effective field theory (EFT) for the dilaton, built upon a manifestly scale-invariant regularization scheme and connecting ultraviolet conformal behavior to the infrared through a hierarchical tower of operators. We demonstrate universal linear couplings to the trace anomaly and explore the dilaton’s phenomenology across a broad mass spectrum, from conventional particle production at the LHC to ultralight dark matter detectable via atomic precision measurements. Will this unified EFT approach unlock a more complete understanding of the dilaton’s role in addressing fundamental puzzles in particle physics and cosmology?

---

Unveiling the Symmetry Beneath: A Search for Scale Invariance

Despite its remarkable predictive power, the Standard Model of particle physics remains incomplete. While accurately describing the fundamental forces and particles observed at current energy scales, it fails to account for phenomena like dark matter, which constitutes a significant portion of the universe’s mass-energy density. Furthermore, the model offers no explanation for the observed neutrino masses or the matter-antimatter asymmetry. Extrapolating the Standard Model to higher energies also leads to inconsistencies, specifically the hierarchy problem – the vast disparity between the electroweak scale and the Planck scale – suggesting the presence of new physics beyond the model’s current framework. These unresolved questions motivate the search for more comprehensive theories capable of addressing these shortcomings and providing a complete picture of the universe at its most fundamental level.

The pursuit of physics beyond the Standard Model increasingly focuses on the principle of scale invariance, a concept suggesting the laws of nature remain consistent regardless of energy scale. Theories embracing this symmetry offer a compelling framework for addressing shortcomings in the current model, potentially revealing previously unknown particles and interactions. While perfect scale invariance isn’t observed in reality, the approximation-where symmetry is nearly, but not perfectly, upheld-provides a viable pathway for constructing new physics. This approach proposes that the fundamental constants governing particle properties aren’t truly constant, but instead vary subtly with energy, hinting at a deeper, more unified structure underlying the universe. Exploring these nearly scale-invariant theories allows physicists to predict the existence of new particles, such as dilatons, and offers a potential solution to mysteries like the hierarchy problem and the nature of dark matter, opening exciting avenues for future research and experimentation.

While the allure of scale invariance offers a potentially elegant framework for extending the Standard Model, empirical observations firmly demonstrate that perfect scale symmetry is not realized in nature. The masses of fundamental particles, and the strength of interactions, vary across energy scales, indicating a broken symmetry. Understanding how this breaking occurs is therefore paramount. This isn’t simply a matter of adding ad-hoc terms to equations; physicists seek a dynamical mechanism – a fundamental principle – that explains the observed deviations. Current research focuses on identifying the agent responsible for this symmetry breaking, with promising avenues exploring connections to phenomena like the trace anomaly and the potential existence of a new particle, the dilaton, which could act as the mediator of this crucial transition from a perfectly symmetrical, high-energy state to the complex, mass-structured universe observed today.

The apparent violation of scale invariance in the Standard Model isn’t necessarily a flaw, but rather a signal of richer underlying physics. Calculations reveal a quantum mechanical effect known as the trace anomaly, which subtly breaks classical scale symmetry; this anomaly hints at the existence of a previously unobserved particle – the dilaton. This dynamical scalar field arises as a consequence of the anomaly and effectively ‘eats’ the would-be Goldstone boson associated with scale transformations, gaining a mass and mediating interactions that could explain phenomena beyond the Standard Model. The dilaton’s properties, including its coupling to other particles, are directly tied to the strength of the trace anomaly, making it a compelling candidate for dark matter or a mediator between visible and hidden sectors of the universe, and offering a potential avenue for resolving some of the persistent mysteries in particle physics.

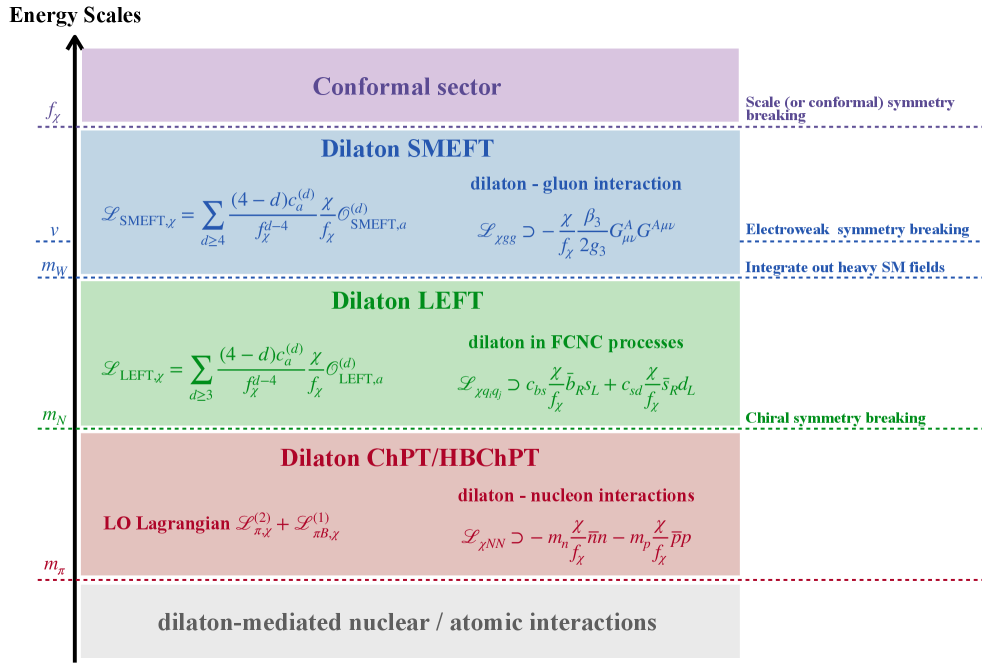
Decoding the Dilaton: An Effective Field Theory Approach

Effective Field Theory (EFT) provides the framework for analyzing dilaton interactions due to the dilaton’s typically weak coupling and the inherent complexities of its quantum behavior. Rather than attempting a full, non-perturbative treatment, EFT allows physicists to construct an expansion in terms of energy and momentum, treating the dilaton as a relatively light pseudo-Nambu-Goldstone boson. This approach necessitates defining an effective Lagrangian incorporating all possible interactions between the dilaton and Standard Model particles, organized by their dimensionality. The coefficients of these interactions, known as Wilson coefficients, parameterize our ignorance of the underlying ultraviolet physics and can be systematically determined through matching to more fundamental theories or experimental data. By focusing on the low-energy degrees of freedom and systematically including higher-order terms, EFT provides a controlled approximation for studying dilaton couplings and predicting its phenomenological effects.

The dilaton’s interactions are fundamentally governed by its coupling to the trace of the energy-momentum tensor, \theta_{\mu\mu}. This coupling dictates how the dilaton affects all sectors of particle physics, as the energy-momentum tensor appears in the equations of motion for all fields. Specifically, the dilaton’s interaction Lagrangian includes terms proportional to the trace of the energy-momentum tensor multiplied by the dilaton field itself, effectively modifying the masses and couplings of other particles. The strength of this coupling determines the dilaton’s influence on gravitational phenomena and its role in potentially solving the hierarchy problem by dynamically adjusting cosmological constant values.

The Renormalization Group (RG) is essential for characterizing the energy dependence of dilaton couplings. These couplings are not constant but ‘run’ with the energy scale μ at which interactions are probed; the RG provides the framework to calculate these variations. Specifically, the β-functions, derived through the RG, quantify the rate of change of a coupling constant g(\mu) with respect to the energy scale: \mu \frac{dg}{d\mu} = \beta(g) . Analyzing these β-functions reveals whether couplings become stronger or weaker at higher energies, impacting the dilaton’s effective interactions and its role in mediating forces between other particles. Precise calculations often necessitate loop corrections and careful consideration of divergences, which the RG systematically addresses through regularization and renormalization procedures.

Scale Invariant Regularization is a technique employed to maintain scale invariance throughout calculations in quantum field theory, particularly when dealing with divergences. This is achieved by explicitly ensuring that all quantities remain dimensionless under rescaling of coordinates. A common implementation utilizes a Λ dependent metric, introduced via a “Conformal Compensator” field. This field transforms alongside the metric, effectively cancelling any scale-dependent divergences that would otherwise violate scale invariance. The compensator field ensures that correlation functions and other observables remain well-defined and scale invariant even after renormalization, allowing for consistent calculations in theories where scale invariance is a fundamental principle or desired symmetry.

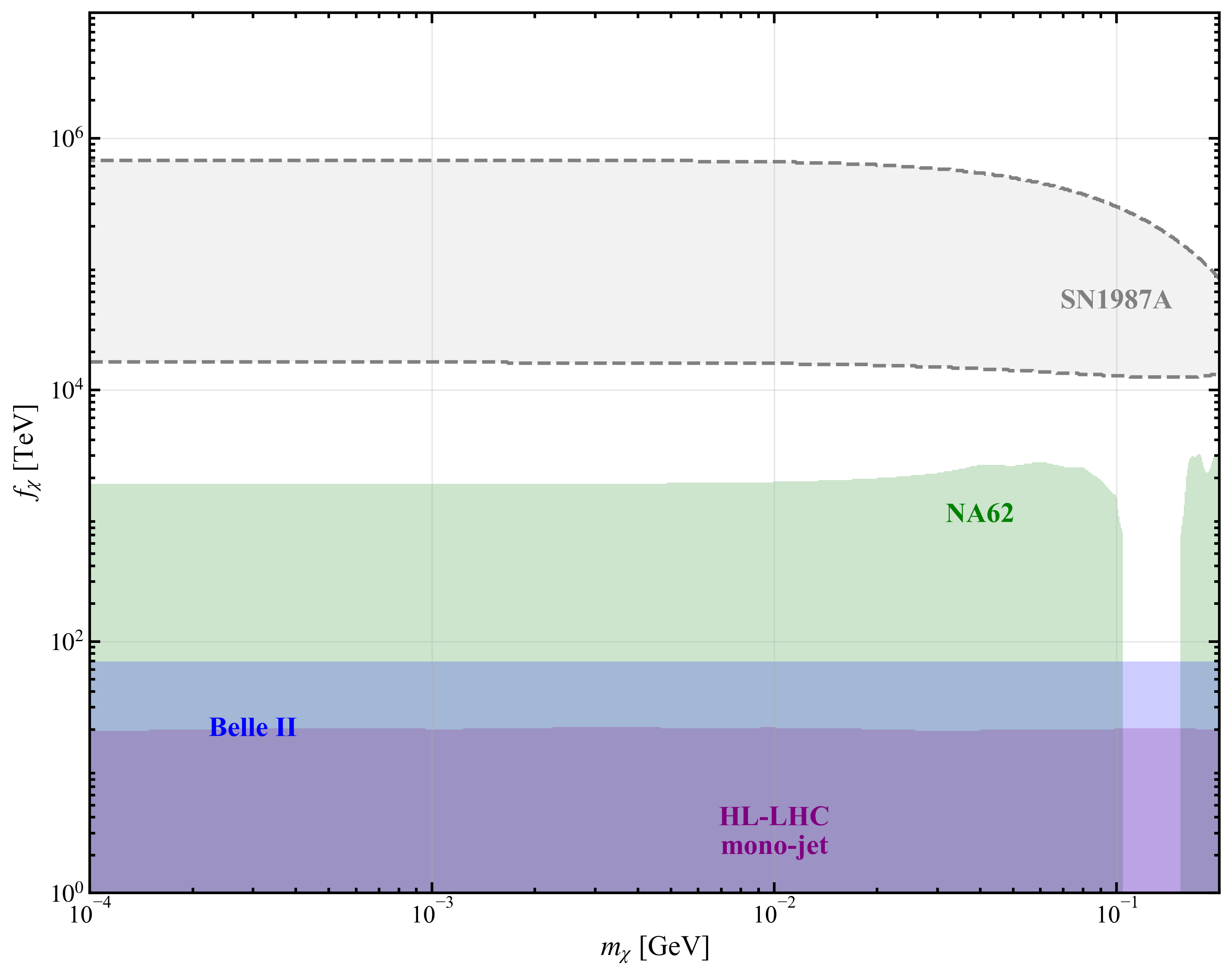
Tracing the Influence: From SMEFT to Chiral Perturbation Theory

Standard Model Effective Field Theory (SMEFT) offers a framework for systematically analyzing potential deviations from the Standard Model predicted by new physics. This is achieved by introducing higher-dimensional operators, suppressed by a characteristic energy scale Λ, into the Standard Model Lagrangian. These operators parameterize the effects of new degrees of freedom without requiring a specific ultraviolet completion. Crucially, SMEFT can accommodate the effects of a dilaton, a pseudo-Nambu-Goldstone boson associated with the spontaneous breaking of scale invariance. The dilaton’s couplings to Standard Model particles are described by Wilson coefficients within the SMEFT framework, allowing for quantitative predictions and comparisons with experimental measurements seeking evidence of beyond-the-Standard-Model physics.

Low-Energy Effective Field Theory (LEFT) is derived from the Standard Model Effective Field Theory (SMEFT) through a process of systematically reducing the energy scale considered. This reduction allows for the integration of heavier degrees of freedom, effectively describing their influence through lower-energy interactions. Consequently, LEFT focuses on the relevant dynamics at lower energies, specifically those governing hadronic interactions – the strong force interactions between hadrons such as protons, neutrons, and mesons. The framework utilizes an expansion in powers of p/Λ_{χ}, where p represents the momentum scale of the interaction and Λ_{χ} denotes the chiral symmetry breaking scale, approximately 1 GeV. This approach enables calculations of hadronic observables without explicitly including the high-energy physics represented in the original SMEFT.

Chiral Perturbation Theory (χPT) is a low-energy effective field theory built upon the spontaneous breaking of chiral symmetry in Quantum Chromodynamics (QCD). It provides a systematic expansion of the QCD Lagrangian in terms of pion fields and their derivatives, allowing for calculations of hadronic interactions at energies well below 1 GeV. Unlike earlier approaches, χPT incorporates the relevant degrees of freedom – mesons and baryons – explicitly, and predicts scattering amplitudes and decay constants based on a limited number of low-energy constants. The order of the expansion is determined by the number of pion fields in the Lagrangian, with O(p^n) representing terms involving n derivatives of the pion fields. This framework allows for precise calculations of processes like pion-pion scattering, and provides a crucial link between the underlying QCD dynamics and observable hadronic properties at low energies.

The Low-Energy Effective Field Theory (LEFT) framework enables the systematic study of the Dilaton-Baryon coupling, a parameter quantifying the interaction between the dilaton field and baryons. This coupling is critical because it directly impacts observable hadronic properties such as masses, scattering amplitudes, and decay rates. LEFT provides a means to calculate these effects, allowing for precise comparisons with experimental data from facilities like CERN and Jefferson Lab. Specifically, the coupling manifests as modifications to baryon masses and introduces novel contributions to \pi N and N N scattering, providing a pathway to indirectly probe the dilaton and constrain potential beyond-the-Standard-Model physics.

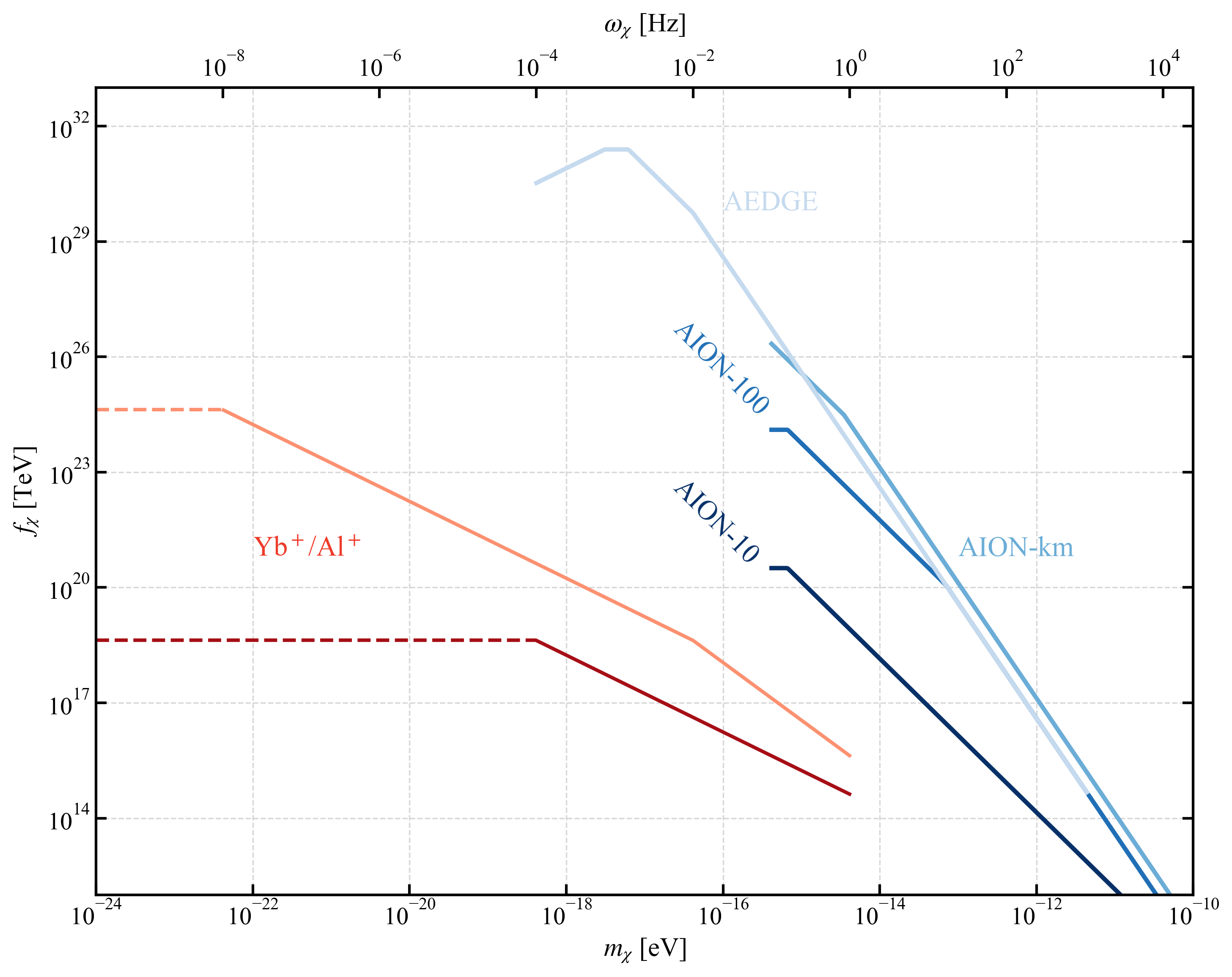
The pursuit of a robust effective field theory, as demonstrated in this study of the light dilaton, necessitates a holistic understanding of interconnectedness. Just as a biological system’s health relies on the harmonious function of its parts, so too does the theoretical consistency of this model depend on carefully charting the dilaton’s interactions with Standard Model particles. This approach mirrors the sentiment expressed by John Dewey: “Education is not preparation for life; education is life itself.” Similarly, this theoretical work isn’t merely a prelude to experimental verification; it is the exploration of fundamental principles unfolding within the framework of scale invariance and chiral symmetry, a dynamic process of refinement and understanding.

Beyond the Simplest Models

The development of a consistent effective field theory for the dilaton, as presented, feels less like a destination and more like the careful charting of a previously obscured coastline. The immediate parameter space, while constrained, remains stubbornly large, hinting at a deeper underlying structure yet to be revealed. If the system survives on duct tape-meaning, if the current constraints rely heavily on specific simplifying assumptions about ultraviolet completions-it’s probably overengineered. The real challenge isn’t simply refining the existing couplings, but determining if the dilaton truly is a fundamental particle, or merely an emergent phenomenon arising from a more complex dynamical regime.

A crucial next step involves a more rigorous investigation of the dilaton’s interplay with chiral symmetry. The current approach, while functional, treats this connection somewhat as an afterthought. Modularity without context is an illusion of control; understanding how scale invariance breaking impacts the full chiral Lagrangian will be vital. Further, the sensitivity of dilaton phenomenology to the specific choice of renormalization group scale demands careful consideration, and possibly a paradigm shift in how these calculations are approached.

Ultimately, the fate of this program likely rests on experimental verification – or falsification. The precision required to disentangle dilaton signals from Standard Model backgrounds is daunting, but not insurmountable. The pursuit, however, compels a broader philosophical question: are we seeking to fit the dilaton into the Standard Model, or are we uncovering evidence that the Standard Model itself requires fundamental revision?

---

Original article: https://arxiv.org/pdf/2601.16534.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

• Best Controller Settings for ARC Raiders

• Donkey Kong Country Returns HD version 1.1.0 update now available, adds Dixie Kong and Switch 2 enhancements

• Ashes of Creation Rogue Guide for Beginners

• PS5’s Biggest Game Has Not Released Yet, PlayStation Boss Teases

• Sega Insider Drops Tease of Next Sonic Game

• When to Expect One Piece Chapter 1172 Spoilers & Manga Leaks

• Fantasista Asuka launches February 12

• Hytale: Upgrade All Workbenches to Max Level, Materials Guide

• If You Like Stranger Things, You’ll Love This Three-Season Sci-Fi Thriller That Launched Five Years Ago Today

• 32 Kids Movies From The ’90s I Still Like Despite Being Kind Of Terrible

2026-01-27 00:03