The Quantum Preparation Bottleneck

by

Author: Denis Avetisyan

New research establishes fundamental limits on how quickly useful quantum states can be created, impacting the speed of quantum sensing and metrology.

The study establishes a theoretical bound on the time-scaling exponent - denoted as $\beta$ - for preparing metrologically useful entangled states via Hamiltonians exhibiting $1/r^{\alpha}$ spin-spin interactions, demonstrating optimality when $\gamma = 1$ for any $\alpha > 0$ and achieving near-optimal performance-with exponents matching known protocols-for $0 < \gamma < 1$ when $\alpha > (2-\gamma)d$.
The study establishes a theoretical bound on the time-scaling exponent – denoted as $\beta$ – for preparing metrologically useful entangled states via Hamiltonians exhibiting $1/r^{\alpha}$ spin-spin interactions, demonstrating optimality when $\gamma = 1$ for any $\alpha > 0$ and achieving near-optimal performance-with exponents matching known protocols-for $0 < \gamma < 1$ when $\alpha > (2-\gamma)d$.

This review derives rigorous lower bounds on state preparation time, linking it to the quantum Fisher information and demonstrating near-optimality of current methods.

Achieving optimal precision in quantum metrology demands efficient state preparation, yet fundamental limits on this process remain poorly understood. This work, ‘Time complexity in preparing metrologically useful quantum states’, establishes rigorous lower bounds on the time required to generate entangled states for quantum sensing, linking preparation time to the system’s quantum Fisher information and the range of interactions. We demonstrate that preparation time scales with system size in a manner dictated by interaction range, revealing potential speedups for long-range interactions and proving near-optimality for existing protocols. Can these bounds guide the development of more effective quantum sensors and illuminate the ultimate limits of quantum-enhanced precision?

The Erosion of Classical Limits: A Quantum Dawn

Conventional sensing technologies, those built upon classical physics principles, encounter a fundamental barrier to precision known as the Standard Quantum Limit. This limit arises because classical systems are susceptible to inherent noise – random fluctuations that obscure the signal being measured. As the size or complexity of a sensing system increases, so too does this noise, effectively diminishing the signal-to-noise ratio and restricting the ability to detect increasingly subtle changes. For example, measuring a weak magnetic field with a traditional magnetometer becomes less accurate as the instrument’s sensitivity is overwhelmed by thermal noise and other classical disturbances. This poses a significant challenge in fields ranging from medical imaging to materials science, where detecting minute variations is crucial, and necessitates a paradigm shift beyond the constraints of classical measurement techniques.

Quantum metrology represents a paradigm shift in measurement science, offering the potential to overcome the precision limits imposed by classical approaches. Traditional methods are fundamentally constrained by the Standard Quantum Limit, where noise increases proportionally to the signal, hindering the detection of exceedingly weak phenomena. However, by leveraging quantum phenomena such as superposition and, crucially, entanglement, quantum metrology allows for the creation of correlated quantum states. These states exhibit noise characteristics that scale more favorably – often as $1/N$ instead of $1/\sqrt{N}$, where N is the number of particles – leading to a substantial enhancement in measurement precision. This isn’t simply about shrinking error margins; it opens doors to detecting signals previously obscured by noise, with implications spanning fields like medical imaging, materials science, and fundamental physics research, enabling observation of previously inaccessible details and ultimately redefining the boundaries of what can be measured.

Quantum spin sensors represent a pivotal advancement in the field of metrology, offering a uniquely versatile platform for the detection of exceedingly weak signals. These sensors leverage the quantum mechanical properties of electron spins – specifically, their sensitivity to subtle changes in magnetic, electric, and thermal fields – to achieve sensitivities far exceeding those of classical counterparts. Unlike traditional magnetometers which are limited by thermal noise and other classical factors, quantum spin sensors can exploit quantum entanglement and coherence to surpass the Standard Quantum Limit, enabling the detection of signals previously buried in noise. This enhanced sensitivity isn’t limited to a single application; these sensors are proving valuable in diverse areas ranging from biomagnetic imaging – detecting the faint magnetic fields produced by the human heart and brain – to materials science, geological surveying, and even the search for dark matter. The compact size and potential for integration into existing technologies further solidify their role as a cornerstone of future sensing capabilities, promising breakthroughs across numerous scientific and technological disciplines.

Entanglement’s Ascent: Approaching Heisenberg’s Horizon

Classical sensors are fundamentally limited by a precision scaling inversely proportional to the number of particles, $1/N$. This means increasing the number of particles provides a diminishing return in measurement accuracy. However, quantum sensors leveraging entanglement can, in theory, surpass this limit and achieve the Heisenberg Limit, where precision scales as $1/N$. This improvement arises because entanglement correlates the particles in a way that reduces the overall measurement uncertainty. Specifically, the collective quantum state exhibits a lower variance than would be possible with $N$ independent, non-entangled measurements, thereby enabling a higher degree of sensitivity and precision in estimations.

The enhancement of precision in entangled sensors arises from the non-classical correlations present in entangled states, which allow for a reduction in measurement uncertainty below the Standard Quantum Limit (SQL). Classical measurements are limited by uncorrelated noise, resulting in a precision that degrades proportionally to $1/\sqrt{N}$, where N is the number of particles or sensors. Entangled states, however, exhibit correlations that effectively redistribute noise, reducing uncertainty in the parameter being measured. This allows entangled sensors to potentially achieve the Heisenberg Limit, where precision scales as $1/N$. The core principle is that entangled particles behave as a collective, enabling a more accurate determination of a physical quantity than would be possible by independently measuring each particle.

Spin squeezed states are a specific type of entangled state utilized to enhance the precision of parameter estimation in quantum metrology. Their efficacy is quantified by the quantum Fisher Information (QFI), which dictates the ultimate limit of precision achievable in estimating a parameter. For $N$ independent particles, the QFI scales as $F_Q \sim N^{1+\gamma}$, where $\gamma$ is a positive exponent dependent on the specific squeezing technique. This scaling demonstrates a significant improvement over classical sensors, where the QFI is limited to a linear dependence on $N$. The enhancement arises from reducing the uncertainty in one quadrature of the field at the expense of increased uncertainty in the other, effectively concentrating measurement sensitivity and allowing for precision approaching the Heisenberg limit.

Optimal spin-squeezing time and the resulting quantum Fisher information exhibit scaling relationships with the number of spins that differ between one-axis twisting, two-axis twisting, and twist-and-turn protocols, as defined by fitted models with corresponding coefficients.
Optimal spin-squeezing time and the resulting quantum Fisher information exhibit scaling relationships with the number of spins that differ between one-axis twisting, two-axis twisting, and twist-and-turn protocols, as defined by fitted models with corresponding coefficients.

Constraints of the Physical Realm: Local Interactions and Limited Depth

Generating highly entangled states, such as Greenberger-Horne-Zeilinger (GHZ) or W states, typically necessitates that each qubit interacts directly with all other qubits in the system. This all-to-all connectivity requirement poses a significant challenge for current and near-term quantum hardware architectures. Most physical qubit platforms, including superconducting circuits, trapped ions, and neutral atoms, are limited by local interactions, meaning qubits can only directly interact with their immediate neighbors. Implementing all-to-all interactions therefore requires the use of SWAP gates to move quantum information between non-neighboring qubits, increasing circuit complexity, introducing gate errors, and reducing overall fidelity. The number of SWAP gates scales with the system size and the distance between qubits, making the creation of large-scale, strongly entangled states particularly difficult with limited connectivity.

Current quantum computing architectures are fundamentally limited by the physical connectivity and operational capacity of their components. Unlike theoretical models which often assume all-to-all connectivity, physical qubits typically interact only with their immediate neighbors, a constraint known as locality. Furthermore, the number of quantum gates – the basic building blocks of a quantum circuit – that can be reliably applied is limited by factors such as decoherence and gate error rates. These limitations directly impact the complexity of entanglement that can be generated; creating highly entangled states, such as $GHZ$ or $W$ states, requires a significant number of two-qubit gates and long-range connectivity, which becomes increasingly difficult to achieve as the number of qubits scales. Consequently, the achievable entanglement structure in realistic quantum circuits is often restricted to simpler forms or localized entanglement patterns.

Lieb-Robinson Bounds define an upper limit on the speed at which information – specifically, correlations – can propagate through a local quantum system. These bounds state that the influence of a local perturbation at one point in the system is constrained to a region that grows linearly with time and the spatial separation, effectively limiting the “light cone” of correlation propagation. For quantum sensing protocols, understanding these limits is crucial; the achievable sensing precision is directly tied to how quickly and effectively correlations can be established between the sensor and the target system. Protocols relying on long-range entanglement or rapid correlation spread will be fundamentally limited by these bounds, necessitating designs that operate within the constraints of limited depth and local interactions to maximize signal detection and minimize noise.

The Inevitable Passage of Time: Complexity and Correlations

The creation of highly entangled quantum states isn’t instantaneous; the time required for their preparation is fundamentally interwoven with the intricacy of correlations between the participating particles. As entanglement increases, so does the complexity of these correlations, demanding more computational resources and time to establish. This relationship isn’t merely a technical challenge, but a core principle governing the limits of quantum sensing and information processing. Specifically, establishing long-range correlations across a system of $N$ particles necessitates a minimum preparation time that scales with the system’s complexity; simpler correlations can be established quickly, but robust, highly-entangled states-essential for applications like precision metrology-require a correspondingly longer setup time, dictating a lower bound on the achievable sensing precision.

Characterizing entanglement generated through local interactions necessitates a detailed understanding of two-body correlations – the relationships between pairs of particles. These correlations don’t simply indicate a connection, but fundamentally define the structure and strength of the resulting entangled state. Researchers find that by meticulously mapping these pairwise relationships, one can effectively predict the overall entanglement properties, even in complex many-body systems. This approach bypasses the need to analyze the exponentially large Hilbert space associated with multiple particles, offering a computationally feasible pathway to quantify entanglement. Moreover, the precise nature of these two-body correlations directly influences the achievable precision in quantum sensing protocols, as they dictate how effectively quantum information can be encoded and measured, highlighting their critical role in harnessing entanglement for practical applications.

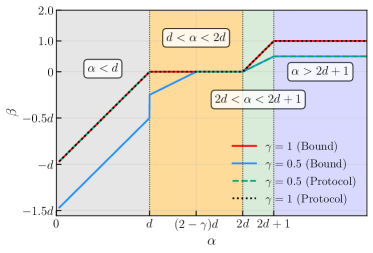
Recent research demonstrates a fundamental constraint on the speed at which highly entangled states – crucial for precision sensing – can be created. The study reveals that, for optimal protocols achieving full Heisenberg scaling ($\gamma=1$), the minimum time required to prepare such states scales as $t \gtrsim 1/N$, where $N$ represents the number of particles. This finding establishes a lower bound on state preparation time, directly impacting the ultimate precision achievable in sensing applications. Essentially, as the number of particles increases, the time needed to create the necessary entanglement grows inversely proportional to that number, highlighting a physical limit to how quickly and sensitively a system can respond to external stimuli. This constraint is not merely a technological hurdle, but a consequence of the inherent relationship between entanglement, complexity, and the speed of information processing within quantum systems.

The efficiency with which highly entangled states can be created is fundamentally limited by the size of the system and the desired precision of measurement. Research indicates that the minimum time, $t$, required to prepare such a state scales with the linear system size, $L$, and a parameter, $\gamma$, directly linked to the Quantum Fisher Information (QFI) scaling. Specifically, the preparation time is bound by the inequality $t \gtrsim L\gamma$. This means that as the system grows larger, or as the desired precision-represented by $\gamma$-increases, the time needed to create the entangled state also increases proportionally. This bound isn’t merely a practical limitation; it establishes a theoretical constraint on the speed at which quantum sensors can operate, impacting the ultimate precision achievable in measurements relying on these entangled states.

The pursuit of optimized state preparation, as detailed in the study of time complexity concerning metrologically useful quantum states, inherently acknowledges the constraints within which all systems operate. It isn’t merely about achieving faster preparation, but understanding the fundamental limits dictated by quantum Fisher information and Lieb-Robinson bounds. This resonates with the notion that systems don’t simply ‘fail’ but progress through defined steps, even if those steps manifest as increased complexity. As Werner Heisenberg observed, “The very act of observing changes the observed.” This principle mirrors the study’s findings; the attempt to define and optimize preparation time inevitably influences the system itself, revealing the inherent interplay between measurement, control, and the unavoidable march toward entropy. The study doesn’t propose conquering time, but navigating its constraints with increasing finesse.

The Inevitable Margin

The established lower bounds on state preparation time, linked as they are to the quantum Fisher information, offer a crucial, if sobering, perspective. These are not merely constraints on current protocols, but fundamental limits imposed by the flow of quantum information itself. Uptime for any metrological gain is, after all, temporary. The demonstration of near-optimality in existing schemes doesn’t suggest an end to inquiry, but rather a sharpening of the question: what is the true cost of precision? Each request for enhanced sensitivity pays a tax in latency-a principle increasingly relevant as systems scale.

Future work will undoubtedly refine these bounds, exploring the interplay between interaction range and achievable precision. However, the true challenge may lie in accepting the inherent trade-offs. The pursuit of ever-decreasing preparation times will likely encounter diminishing returns, as any attempt to circumvent the established limits merely redistributes the computational burden.

Stability is an illusion cached by time. The field must now shift focus from simply achieving squeezed states to understanding their fragility, their susceptibility to decoherence, and ultimately, the lifespan of any metrological advantage. The cost of information is not merely in its acquisition, but in its preservation-a principle often overlooked in the rush to push the boundaries of what is possible.

Original article: https://arxiv.org/pdf/2511.14855.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-11-21 01:07