Time’s Entangled Web: Exploring Holographic Connections

Author: Denis Avetisyan

New research delves into how quantum entanglement evolves in time within complex systems, offering insights into the emergence of time itself.

The study reveals that the imaginary component of pseudo-entropy <span class="katex-eq" data-katex-display="false">Sp^{I}_{pA} </span> exhibits opposing behaviors contingent upon the sign of the anisotropy parameter <span class="katex-eq" data-katex-display="false">\Delta_{y} </span>, demonstrated through variations in <span class="katex-eq" data-katex-display="false">\beta|\Delta| </span> at <span class="katex-eq" data-katex-display="false">\beta = 10 </span> with <span class="katex-eq" data-katex-display="false">\delta_{x} </span> and <span class="katex-eq" data-katex-display="false">\delta_{y} </span> set to specific values, suggesting a fundamental sensitivity within the system to directional asymmetry. — The study reveals that the imaginary component of pseudo-entropy $Sp^{I}_{pA}$ exhibits opposing behaviors contingent upon the sign of the anisotropy parameter $\Delta_{y}$ , demonstrated through variations in $\beta|\Delta|$ at $\beta = 10$ with $\delta_{x}$ and $\delta_{y}$ set to specific values, suggesting a fundamental sensitivity within the system to directional asymmetry.

This review investigates holographic time-like entanglement entropy and pseudo-entropy in anisotropic backgrounds within the framework of the AdS/CFT correspondence.

The subtle interplay between entanglement, time, and strongly coupled systems remains a central challenge in modern theoretical physics. This is explored in ‘On Holographic Time-Like Entanglement Entropy’, which compares holographic time-like entanglement entropy with pseudo-entropy for a two-qubit system undergoing transitions to anisotropic thermal states. The analysis reveals a complex relationship between anisotropy, quantum correlations, and the emergence of time within the framework of the $AdS/CFT$ correspondence. How might these findings illuminate the broader connection between quantum information and the geometry of spacetime in more realistic, relativistic settings?

The Fragility of Equilibrium: Unveiling Hidden Correlations

Conventional entanglement entropy, a cornerstone for quantifying quantum connections, faces significant challenges when applied to systems distant from equilibrium. These measures, often reliant on assumptions of static or slowly varying states, struggle to accurately represent the rapidly fluctuating correlations inherent in complex quantum systems. The limitations stem from the difficulty in defining a clear boundary between subsystems and the inability to capture the dynamic, many-body interactions that drive these correlations. Consequently, standard entropy calculations may underestimate the true degree of entanglement, obscuring crucial information about the system’s behavior and hindering a complete understanding of phenomena like high-temperature superconductivity or the quark-gluon plasma, where strong interactions and non-equilibrium dynamics are prevalent. This inadequacy necessitates the development of more sophisticated tools capable of characterizing the intricate web of correlations that define these exotic states of matter.

The inability of standard entanglement entropy to fully capture quantum correlations presents a significant obstacle to progress in fields grappling with strongly correlated phenomena. In high-energy physics, understanding the quark-gluon plasma – a state of matter existing moments after the Big Bang – demands a precise accounting of particle interactions, which are often governed by these complex correlations. Similarly, within condensed matter physics, exotic materials like high-temperature superconductors and topological insulators exhibit behaviors dictated by the collective, entangled dance of electrons; traditional entropy measures fail to fully characterize these states, hindering the design of novel materials with tailored properties. Effectively, a limited view of these correlations translates directly into an incomplete understanding of the fundamental physics driving these systems, necessitating new theoretical tools and experimental probes to unlock their secrets.

The exploration of exotic states of matter-from the superfluids exhibiting frictionless flow to the enigmatic quantum spin liquids-demands analytical tools beyond those offered by traditional entanglement entropy. Current measures often falter when confronted with the intricate, long-range correlations present in strongly interacting quantum systems. Consequently, researchers are actively developing more generalized frameworks for quantifying these connections, seeking to capture the full spectrum of quantum relationships. These advanced approaches aim to move beyond simply identifying entangled pairs, instead focusing on characterizing the overall structure of correlations within a system. Such a refined understanding is crucial not only for accurately describing these novel materials but also for potentially harnessing their unique properties in future technologies, opening doors to advancements in quantum computing and materials science. The development of these new tools promises a deeper insight into the fundamental nature of quantum matter and the emergent phenomena arising from its complex interactions.

A Gravitational Mirror: Holographic Duality and Quantum Systems

The Anti-de Sitter/Conformal Field Theory (AdS/CFT) correspondence is a conjectured duality between a quantum field theory without gravity residing on the boundary of a space, and a theory of gravity – specifically, string theory or quantum gravity – in the higher-dimensional Anti-de Sitter (AdS) space. This mapping is particularly useful for analyzing strongly coupled quantum systems, where traditional perturbative methods fail. In these systems, interactions between particles are strong enough to invalidate approximations used in standard quantum field theory calculations. The AdS/CFT correspondence allows physicists to translate problems about these strongly coupled quantum systems into equivalent, and often more tractable, problems in classical gravity, leveraging the well-understood mathematical tools of general relativity to gain insights into quantum phenomena. This is because gravity in AdS space is often weakly coupled even when the corresponding quantum field theory is strongly coupled, providing a computational advantage.

The AdS/CFT correspondence enables the calculation of quantum entanglement-a fundamentally quantum mechanical property-through geometric properties within the corresponding gravitational spacetime. Specifically, entanglement between regions in the boundary quantum field theory is directly related to the geometry of a minimal surface in the higher-dimensional, gravitational “bulk” spacetime that anchors at the boundary of the quantum system. This connection isn’t merely analogical; the amount of entanglement – quantified by the entanglement entropy – is precisely determined by the area of this minimal surface, effectively translating a quantum information-theoretic quantity into a classical geometric measurement. S_{EE} = \frac{A_{min}}{4G_N}[/latex], where S_{EE}[/latex> is the entanglement entropy, A_{min}[/latex> is the area of the minimal surface, and G_N[/latex> is Newton’s gravitational constant.

The Ryu-Takayanagi (RT) formula establishes a direct relationship between the entanglement entropy of a region $R$ in a conformal field theory (CFT) and the area of a minimal surface γ in the associated anti-de Sitter (AdS) spacetime, with γ being homologous to the boundary of $R$ . Specifically, the entanglement entropy $S$ is proportional to the area of γ divided by $4G_N$ , where $G_N[/latex> is Newton's gravitational constant in the bulk AdS spacetime: [latex]S = \frac{Area(\gamma)}{4G_N}$ . This provides a computational tool; rather than directly calculating entanglement entropy-a typically difficult task for strongly coupled systems-one can instead find the minimal surface in the gravitational dual and compute its area. Extensions to the original RT formula address cases involving time dependence and excited states, often requiring knowledge of the extremal surface instead of the minimal surface.

Beyond Static Views: Time-Like Entanglement and Anisotropic Geometries

Holographic time-like entanglement entropy represents an extension of the Ryu-Takayanagi formula, traditionally used to calculate entanglement entropy for spatial separations, to scenarios where the entangled regions are separated in time. The original Ryu-Takayanagi formula relies on minimal surface calculations in a gravitational background to determine entanglement entropy; the time-like extension necessitates considering time-dependent geometries and adapting the minimal surface prescription to accommodate temporal separations. This allows for the quantification of quantum correlations between regions at different moments in time, providing a framework for studying the dynamics of entanglement and its relationship to spacetime geometry. The resulting entropy is calculated by finding the minimal time-like surface connecting the entangled regions in the bulk gravitational theory, yielding a measure of their temporal correlation.

Calculating holographic time-like entanglement entropy necessitates the use of anisotropic background metrics because these metrics accurately represent directional dependencies present within the quantum system being modeled. Isotropic metrics, which assume homogeneity in all directions, are insufficient to capture correlations between time-separated regions when those regions exhibit differing properties based on spatial orientation. An anisotropic metric, mathematically described by differing components in the $g_{\mu\nu}$ tensor, allows for the precise modeling of these directional dependencies, thereby enabling an accurate computation of entanglement entropy that accounts for the system’s inherent asymmetries and their influence on quantum correlations. The specific form of the anisotropy directly impacts the calculated entanglement, requiring careful consideration of the metric components to reflect the underlying quantum system.

Analysis of anisotropic background metrics demonstrates a non-monotonic relationship between the anisotropy parameter, $a$ , and the magnitude of quantum correlations. Specifically, calculations reveal that increasing $a$ initially decreases correlation strength, reaching a minimum value at an intermediate $a$ . Beyond this minimum, further increases in $a$ result in a subsequent increase in the strength of quantum correlations. This behavior indicates that anisotropy does not simply amplify or diminish correlations linearly, but rather modulates their strength in a more complex, parameter-dependent manner.

Probing Extreme Matter: From Theory to the Quark-Gluon Plasma

Theoretical physicists employ anisotropic background metrics within holographic calculations to construct a robust framework for modeling Quark-Gluon Plasma (QGP). This approach arises from the need to represent the QGP, a state of matter created in high-energy heavy-ion collisions, which isn't simply a homogenous fluid but exhibits directional dependencies-anisotropy-in its pressure and flow. By leveraging the holographic principle-a conjecture linking gravity and quantum field theory-researchers can map strong interactions within the QGP to a gravitational problem with these anisotropic backgrounds. These backgrounds, solutions to Einstein’s equations, then allow for the calculation of QGP properties, offering insights into its behavior at extreme temperatures and densities-conditions far beyond those achievable in conventional laboratories. The resulting models provide a crucial bridge between theoretical predictions and experimental observations from facilities like the Relativistic Heavy Ion Collider and the Large Hadron Collider, furthering understanding of the strong force governing matter at its most fundamental level.

Holographic methods present a unique pathway to investigate the extraordinarily dense and hot Quark-Gluon Plasma (QGP), a state of matter created in high-energy heavy-ion collisions. This approach leverages the duality between gravitational theories and quantum field theories, allowing researchers to model the QGP’s complex thermal characteristics and intricate particle correlations through calculations in a more tractable gravitational framework. Specifically, analyses conducted at temperatures of 10 and 2.3 - representing a significant range within QGP’s expected thermal profile - reveal how holographic techniques can capture the dynamic interplay between energy, momentum, and quantum entanglement within this extreme environment. These investigations provide valuable insights into the fundamental properties of strongly coupled matter, offering a complementary perspective to traditional experimental and theoretical approaches and potentially unlocking new understandings of the early universe and the nature of nuclear forces.

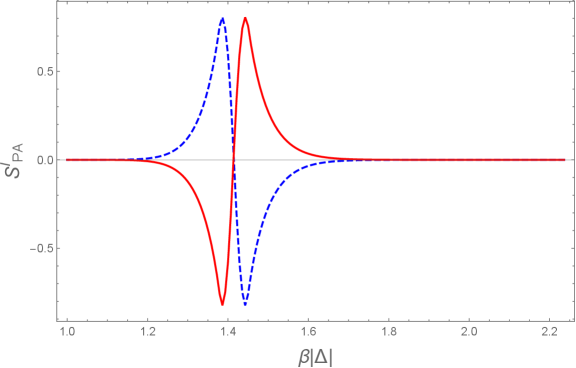
Calculations reveal a fascinating dynamic within the Holographic Time-like Entanglement Entropy (HTEE) when subjected to varying degrees of anisotropy in extreme matter. Initially, the imaginary component of HTEE diminishes as anisotropy increases, suggesting a weakening of quantum entanglement. However, this trend reverses; under certain conditions, the imaginary part of HTEE becomes positive. This positive value indicates a reorganization of quantum correlations, implying that the system transitions from decreasing to increasing entanglement as anisotropy intensifies. This behavior challenges conventional expectations and suggests that highly anisotropic conditions can actually enhance quantum connectedness within the Quark-Gluon Plasma, potentially influencing its thermal properties and collective behavior. The shift from negative to positive values in the imaginary component of $HTEE$ represents a fundamental change in how quantum information is distributed within this exotic state of matter.

Beyond Standard Correlations: Pseudo-Entropy and Future Directions

Pseudo-entropy represents a significant advancement in quantifying correlations, extending beyond the limitations of traditional entanglement entropy which is primarily designed for standard quantum systems. While entanglement focuses on the connections between qubits, pseudo-entropy offers a more generalized framework capable of describing correlations in systems exhibiting complex connections and higher-order interactions-systems where simple pairwise entanglement may not fully capture the relationship between constituents. This generalization is achieved through a mathematical construction that doesn't require the strict adherence to Hilbert space formalism, allowing it to be applied to a broader range of physical scenarios, including those found in condensed matter physics and potentially even beyond. Consequently, pseudo-entropy offers a powerful tool for characterizing and understanding complex quantum phenomena where correlations are not limited to the binary entanglement found in simpler systems, potentially revealing hidden order and behavior.

The utility of pseudo-entropy stems from its foundation in the Transition Matrix, a mathematical object capable of characterizing the interconnectedness within complex quantum systems. This matrix doesn’t simply measure pairwise correlations; it maps how quantum information flows and transforms across multiple connected components, providing a holistic view of system-wide relationships. Consequently, pseudo-entropy, built upon this framework, reveals insights into the behavior of systems where traditional entanglement measures fall short - such as those with long-range interactions, many-body localization, or topological order. By analyzing the structure of the Transition Matrix, researchers can begin to understand how complex connections give rise to emergent phenomena and novel quantum phases of matter, opening avenues for designing and controlling systems with tailored connectivity.

Recent investigations reveal a compelling parallel between the imaginary component of pseudo-entropy and that of higher-dimensional topological entanglement entropy (HTEE). This shared characteristic becomes particularly pronounced at increased anisotropy, indicating a fundamental reorganization of quantum correlations within these systems. The observed consistency suggests that pseudo-entropy isn't merely an extension of entanglement entropy to broader contexts, but offers a potentially unified framework for comprehending complex correlations across diverse quantum systems-including those beyond the standard models typically employed in quantum field theory. This finding opens avenues for exploring connections between seemingly disparate areas of physics and may provide new tools for characterizing and understanding quantum phenomena in materials science and condensed matter physics.

The pursuit of holographic time-like entanglement entropy, as detailed in this work, echoes a humbling truth about theoretical construction. One might observe that every attempt to quantify quantum correlations, even within the elegant framework of AdS/CFT correspondence, remains provisional. As Michel Foucault noted, “There is no power relation without resistance.” Similarly, every theoretical measure of entanglement-pseudo-entropy, time-like entropy-exists until it encounters the resistance of anisotropic backgrounds or the complexities of strongly coupled systems. The calculations presented here aren’t final pronouncements, but rather fleeting glimpses of order before the inevitable dissolution of the model beyond its event horizon.

The Horizon Beckons

The calculations concerning time-like entanglement and pseudo-entropy in these anisotropic geometries offer little more than a refined map of the territory between what is known and what is not. The persistent difficulty in cleanly separating the emergence of time from the specific details of the strongly coupled system suggests the division itself may be a convenient fiction. When a theory constructs an 'emergence,' the cosmos rarely offers a clear accounting.

Further exploration will inevitably confront the limitations of the AdS/CFT correspondence as a universal solvent. Each attempt to extend these holographic methods to less-idealized backgrounds risks revealing not deeper truths, but the inherent fragility of the mapping. The pursuit of entanglement as a fundamental resource, even in these highly theoretical spaces, is not a conquest, but a careful observation of how information dissipates.

The real question, one rarely articulated, concerns the meaning of ‘information’ itself when considered at the scale of event horizons. A precise measurement is not a dominion over the unknown; it is merely a temporary reprieve before the inevitable return to uncertainty. The calculations continue, of course, but it is worth remembering that when a result is hailed as a discovery, the cosmos smiles, and then swallows it again.

Original article: https://arxiv.org/pdf/2601.17810.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/