Topological Waves at Material Boundaries

Author: Denis Avetisyan

New research reveals how magnetic Weyl semimetals can host unique, localized waves with potential for advanced photonic technologies.

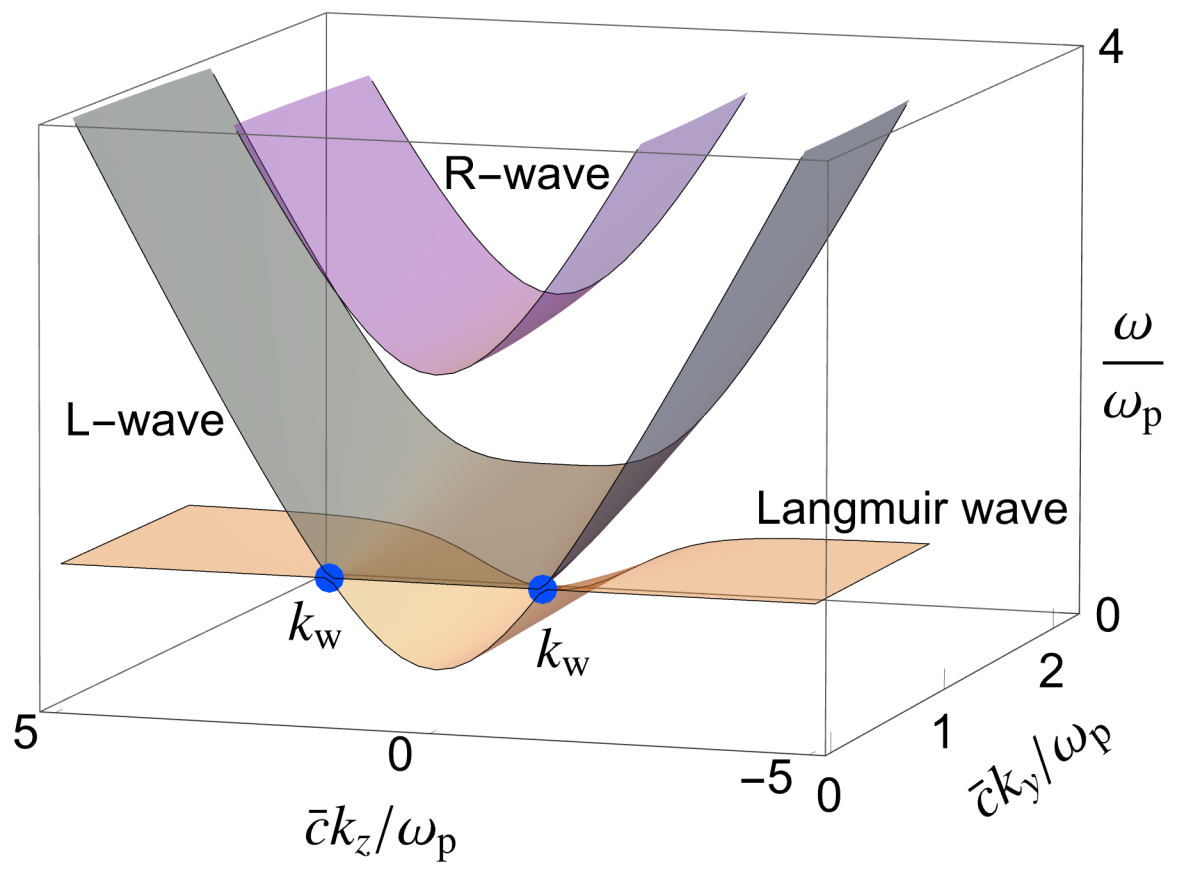
In a magnetic Weyl semimetal, magnetoplasma waves disperse into longitudinal Langmuir oscillations and circularly polarized transverse modes of distinct helicity, exhibiting decoupled behavior along the gyrotropic axis and coinciding with the formation of Weyl node pairs-a phenomenon indicative of the material's unique electronic topology. — In a magnetic Weyl semimetal, magnetoplasma waves disperse into longitudinal Langmuir oscillations and circularly polarized transverse modes of distinct helicity, exhibiting decoupled behavior along the gyrotropic axis and coinciding with the formation of Weyl node pairs-a phenomenon indicative of the material’s unique electronic topology.

This study demonstrates topologically protected magnetoplasma waves confined to domain walls in magnetic Weyl semimetals, linked to the anomalous Hall effect.

Conventional magnetoplasma systems require impractical magnetic fields to support topologically protected wave phenomena, hindering their technological application. This limitation is addressed in ‘Weyl magnetoplasma waves in magnetic Weyl semimetals’, which demonstrates that these materials host unique wave dynamics at zero field due to their intrinsic anomalous Hall effect. The resulting topology supports nonreciprocal modes localized at magnetic domain walls, including novel “Fermi-arc-like” states with potential for robust information transfer. Could these findings pave the way for a new generation of low-power, topologically protected photonic devices?

Unveiling the Topology of Electronic Motion

The Anomalous Hall Effect (AHE) signifies a departure from established principles of classical transport, challenging the long-held assumption that a magnetic field is required to induce a Hall voltage. In materials exhibiting AHE, a measurable voltage develops perpendicular to both the applied current and the direction of magnetization, even without an external magnetic field. This phenomenon indicates that the electron’s motion is intrinsically affected by the material’s band structure, necessitating a deeper investigation beyond simple Drude models which assume parabolic bands and scattering-dominated transport. The inability of classical theory to account for AHE highlights the importance of considering the internal properties of materials – specifically the topology of their electronic bands – to fully understand charge carrier behavior and predict novel electronic responses. Consequently, research has shifted toward exploring the role of band topology and related concepts, like Berry curvature, as fundamental drivers of this unusual effect.

Conventional understandings of the Anomalous Hall Effect (AHE) frequently rely on scattering mechanisms – the deflection of electrons by imperfections or impurities within a material. However, these scattering-based models often prove inadequate when describing the AHE observed in a growing number of materials, particularly those exhibiting large or unusual Hall resistivities. The predicted magnitudes of the AHE based solely on scattering are often significantly lower than experimental results, and these models struggle to account for behaviors like the insensitivity of the AHE to temperature or the emergence of intrinsic contributions without external magnetic fields. This discrepancy suggests that the origins of the AHE are more complex than simple scattering events, necessitating a deeper investigation into the fundamental properties of the material’s electronic structure to fully explain the observed phenomena.

The Anomalous Hall Effect (AHE), a deviation from classical expectations in how materials respond to magnetic fields, finds a compelling explanation in the topological properties of a material’s electronic band structure. Specifically, the concept of Berry curvature – a measure of the geometric properties of these bands – provides a robust mechanism for generating an intrinsic AHE, independent of scattering events. This curvature effectively acts as a fictitious magnetic field experienced by electrons, causing them to deflect even without an applied external field. Materials with non-trivial band topology, characterized by this significant Berry curvature, exhibit a pronounced AHE proportional to the integral of this curvature over the Brillouin zone. Consequently, understanding and engineering these topological features offers a pathway to predict and control the magnitude and sign of the AHE, opening doors for novel spintronic devices and materials with tailored magnetic responses.

The analytical spectrum reveals that confining Majorana propagating (MP) waves exhibits two topological domain wall (DW) modes (blue and red) consistent with bulk-edge correspondence, as described by Eq. <span class="katex-eq" data-katex-display="false">(8)</span>. — The analytical spectrum reveals that confining Majorana propagating (MP) waves exhibits two topological domain wall (DW) modes (blue and red) consistent with bulk-edge correspondence, as described by Eq. $(8)$ .

Magnetic Weyl Semimetals: A Topological Playground

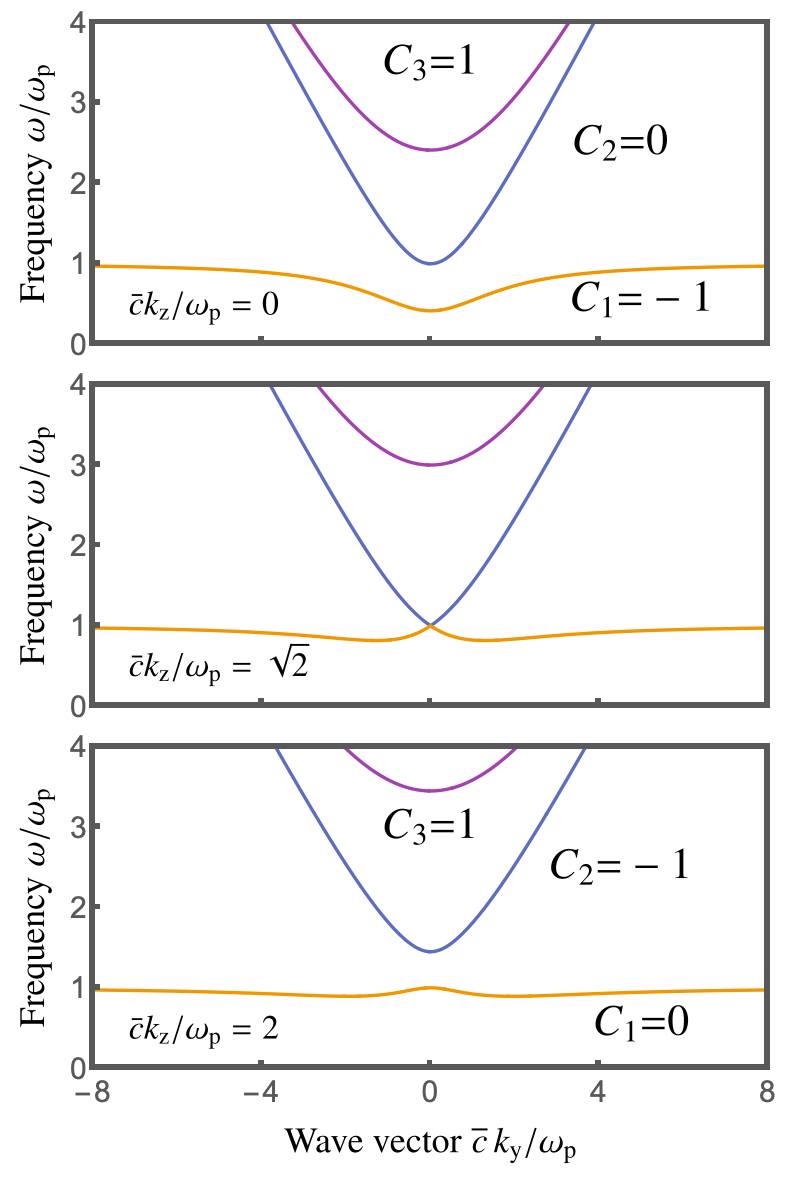
Weyl semimetals are characterized by band structures featuring Weyl nodes, which are points where two non-degenerate bands linearly cross in momentum space. These nodes are topologically protected, meaning their existence is guaranteed by the material’s band topology and are not easily removed by perturbations. Unlike Dirac or conical points, Weyl nodes always appear in pairs of opposite chirality, a property stemming from the underlying symmetry constraints. The nontrivial topology associated with these nodes gives rise to a variety of exotic electronic properties, including large Berry curvature and the presence of surface Fermi arcs. Introducing magnetism into these materials – creating magnetic Weyl semimetals – further enhances these topological effects by breaking time-reversal symmetry and lifting band degeneracies, leading to increased control over the electronic structure and potential applications in spintronics and quantum computing.

Fermi-Arc States are conducting surface states that originate directly from the Weyl nodes in magnetic Weyl semimetals. Unlike conventional surface states which are confined to the material’s boundary, Fermi-Arcs extend across the entire surface, forming open trajectories that connect the projections of Weyl nodes with opposite chirality. These states are protected by the non-trivial topology of the Weyl nodes, rendering them robust against backscattering from non-magnetic impurities. Consequently, Fermi-Arc States contribute significantly to surface conductivity and influence the material’s overall transport properties, particularly at low energies, by providing dissipationless current pathways and contributing to phenomena like the chiral anomaly.

The Anomalous Hall Effect (AHE) in magnetic Weyl semimetals is significantly enhanced due to the interplay between the materials’ intrinsic topology and their broken time-reversal symmetry arising from magnetism. Unlike conventional ferromagnetic materials where the AHE is proportional to the magnetization, in Weyl semimetals, the AHE exhibits a much larger response. This is because the chiral anomaly – a quantum mechanical effect linking the parallel transport of electrons and the Chern number of the Weyl nodes – directly contributes to the AHE conductivity. Specifically, the Berry curvature associated with the Weyl nodes, coupled with the magnetization, results in an increased AHE signal that is often orders of magnitude larger than in traditional ferromagnets, and can exhibit a linear dependence on the magnetic field even at low fields. $\sigma_{xy} \propto B$

The observed dispersion of magnetoplasma waves and the associated exchange of topological Chern numbers at branch crossings confirm the waves’ Weyl nature.

Unraveling Wave Dynamics: A Theoretical Framework

Magnetoplasma waves arise from the collective oscillation of electrons in magnetic materials when subjected to an electromagnetic field. These waves are a coupling of electromagnetic waves and plasma oscillations, where the plasma component describes the coherent response of the electron gas. The behavior is dictated by the material’s dielectric properties and the applied magnetic field, resulting in characteristic wave modes and frequencies. Understanding these collective excitations is crucial for characterizing the electronic properties and dynamics within magnetic materials, as they directly reflect the interactions and correlations between electrons and the underlying crystal lattice. The frequency and damping of these waves are sensitive to parameters such as electron density, effective mass, and magnetic field strength, making them a valuable probe for investigating the material’s electronic structure.

An effective Hamiltonian approach provides a mathematically tractable method for modeling magnetoplasma wave dynamics in magnetic Weyl semimetals. This framework utilizes a simplified Hamiltonian, $H_{eff}$ , constructed to capture the essential physics of electron motion within the material’s band structure, including the influence of magnetic fields and topological features. By employing this approach, the complex many-body interactions within the plasma are reduced to a manageable form, allowing for the analysis of wave propagation and the identification of topological effects such as surface states and chiral anomalies. The resulting Hamiltonian facilitates the calculation of wave dispersion relations and polarization characteristics, providing insights into the material’s response to electromagnetic fields and enabling the prediction of novel wave phenomena.

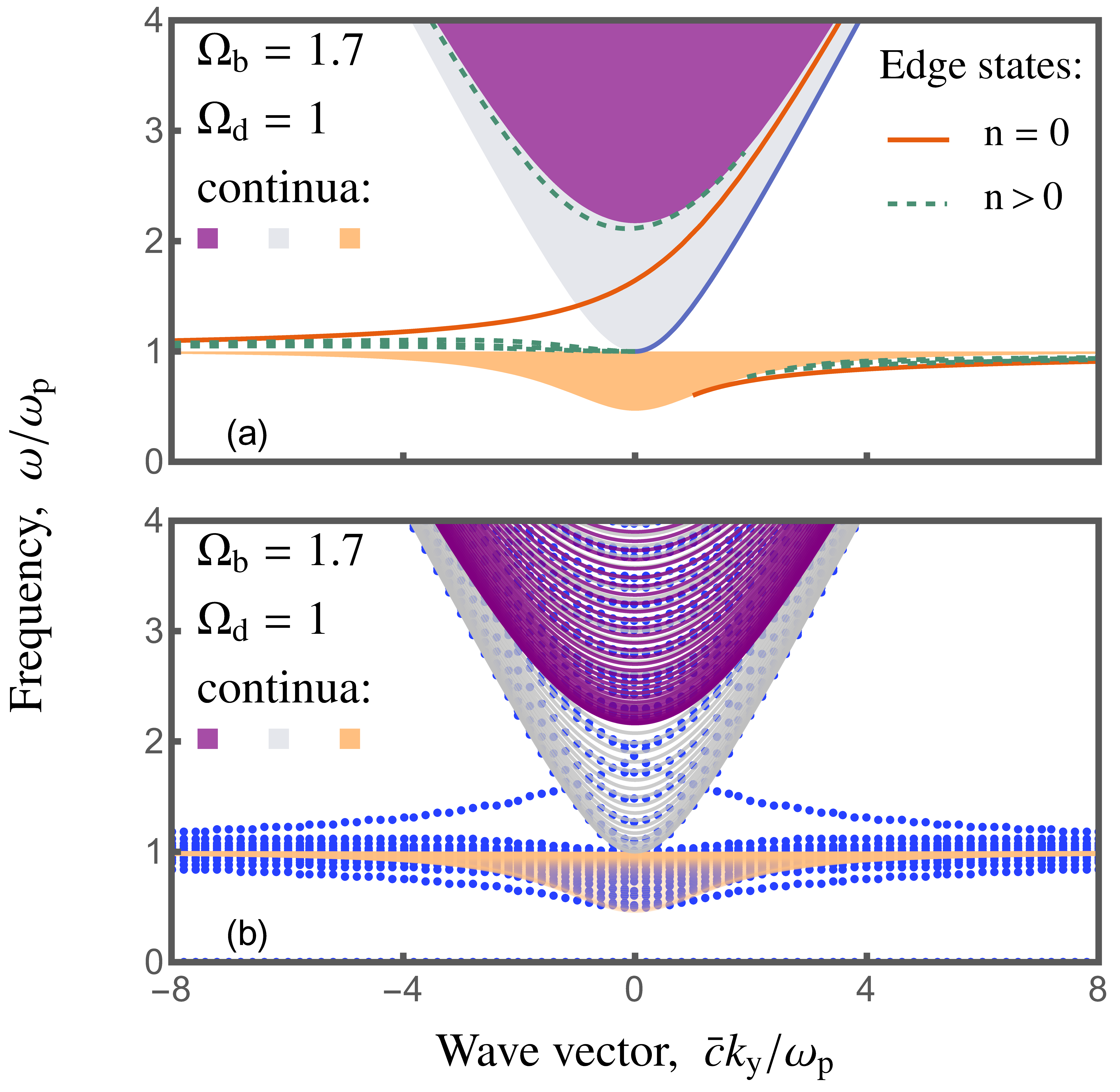
Topological classification of the magnetoplasma wave spectrum within the effective Hamiltonian framework reveals a strong dependence on the material’s Weyl nodes and Fermi arcs. Analysis of Co₃Sn₂S₂, characterized by a plasma frequency $ω_p ≈ 82 \text{ meV}$ and a cyclotron frequency $ω_b ≈ 140 \text{ meV}$ , demonstrates that these topological features directly influence wave propagation characteristics. Specifically, the presence of Weyl nodes leads to localized wave modes and modified dispersion relations, while Fermi arcs introduce surface states contributing to unique wave polarization behavior. This classification allows for prediction of wave behavior as a function of magnetic field and frequency, offering a pathway to manipulate magnetoplasma waves for potential applications in spintronic devices.

The wave spectra for Bloch and Néel domain wall profiles reveal that while Kelvin- and Yanai-like modes initially differ at low <span class="katex-eq" data-katex-display="false">\bar{c}k_{z}/\omega_{p}</span>, their dispersions converge at intermediate and high wave vectors. — The wave spectra for Bloch and Néel domain wall profiles reveal that while Kelvin- and Yanai-like modes initially differ at low $\bar{c}k_{z}/\omega_{p}$ , their dispersions converge at intermediate and high wave vectors.

Domain Walls: Topological Defects and Emergent States

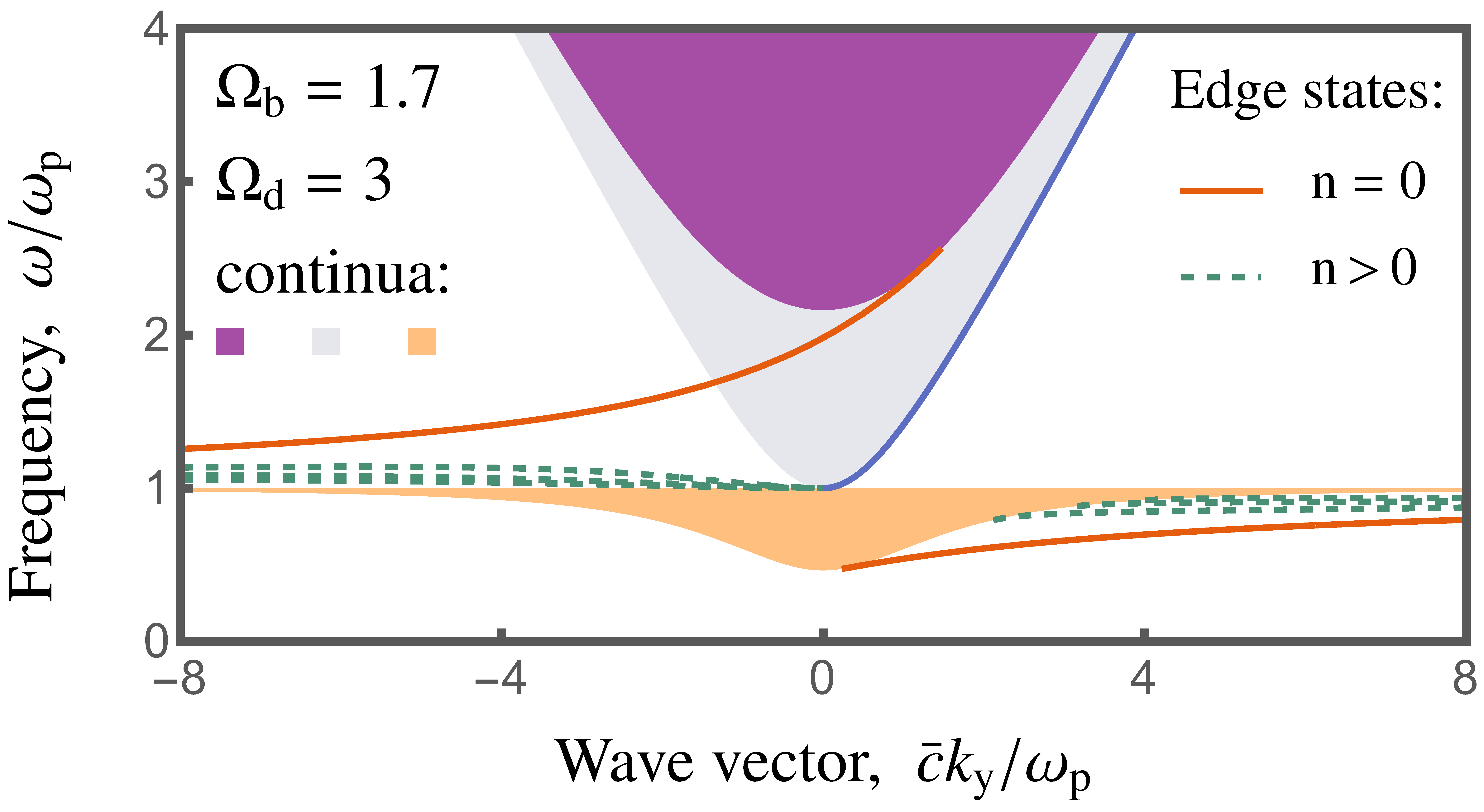
Within the exotic realm of magnetic Weyl semimetals, domain walls emerge not simply as boundaries between magnetic regions, but as topological defects fundamentally altering the material’s electronic structure. These interfaces, where the magnetization abruptly changes direction, represent disruptions in the otherwise orderly spin texture, creating localized states with unique properties. Unlike conventional interfaces, these domain walls possess a non-trivial topology, meaning their characteristics are protected against small perturbations – a resilience stemming from the material’s underlying symmetry. This topological protection makes domain walls robust building blocks for novel spintronic devices, offering a pathway to manipulate and control electron flow with unprecedented precision, and opening possibilities for creating materials with tailored magnetic and electronic responses.

Domain walls within magnetic Weyl semimetals aren’t simply boundaries, but rather host unique electronic states remarkably similar to Volkov-Pankratov states – confined quantum states arising from strong potential gradients. Theoretical modeling demonstrates these localized states can be accurately described using the well-established Pöschl-Teller potential, a mathematical tool for analyzing quantum systems in specific potential wells. Calculations, performed utilizing domain wall widths of 250 nm and 770 nm, reveal that the precise width of the domain wall significantly influences the energy and spatial extent of these localized states, opening avenues for tuning their properties. This ability to mathematically characterize and predictably control these states suggests a pathway toward harnessing domain walls as building blocks for novel nanoscale electronic devices.

The introduction of domain walls within magnetic Weyl semimetals dramatically alters the propagation of magnetoplasma waves, effectively creating pathways for tunable electromagnetic responses. These walls, acting as interfaces between differently magnetized regions, not only scatter and redirect these waves but also directly influence the behavior of Fermi-Arc states – the unique surface states characteristic of Weyl semimetals. Specifically, domain walls can induce localized distortions and modifications to these arcs, leading to enhanced conductivity or even the emergence of entirely new quantum phenomena. This interplay between domain walls, magnetoplasma waves, and Fermi-Arc states opens promising avenues for designing novel spintronic devices and exploring functionalities such as tunable filters, signal modulators, and potentially, even quantum information processing elements – all leveraging the topological properties of these materials.

Analytical (a) and numerical (b) calculations reveal the spectrum of magnetoplasma (MP) waves for a simplified profile, demonstrating distinct behaviors for bulk (shaded regions) and DW-confined (lines) modes at

k_z = 0

Looking Ahead: Harnessing Topological Effects

The Chiral Magnetic Effect (CME) presents a compelling pathway for controlling electrical currents utilizing the inherent topological properties of certain materials. This effect, a close relative of the Anomalous Hall Effect, arises in systems lacking mirror symmetry, causing a charge current to flow along an external magnetic field even without an applied voltage. This isn’t simply a matter of electrons being deflected; the CME is fundamentally linked to the topology of the material’s electronic band structure, where specific quantum states exhibit a chiral, or handedness, characteristic. Researchers are actively exploring how to enhance and control the CME, envisioning devices where charge currents can be steered and manipulated with unprecedented precision, potentially leading to more efficient and compact electronic components and entirely new paradigms in spintronics and beyond. The ability to induce and direct current flow based on topological features, rather than conventional resistance, represents a significant departure from traditional electronics and opens doors to innovative material designs.

Investigations into the dynamic interplay between magnetic domain walls and magnetoplasma waves represent a promising frontier in spintronics. These waves, collective oscillations of electron spins, can be efficiently manipulated by domain walls – the boundaries separating regions of differing magnetization. Researchers posit that by precisely controlling the movement and interaction of these walls with magnetoplasma waves, it may be possible to create devices capable of storing and processing information using spin, rather than charge, dramatically reducing energy consumption and increasing operational speeds. This approach could pave the way for novel memory technologies, logic gates, and sensors with enhanced sensitivity and efficiency, potentially revolutionizing data storage and computation paradigms.

The continued exploration of topological phenomena holds considerable promise for revolutionizing materials science and propelling advancements in quantum technology. These unique material properties, arising from the intricate geometry of their electronic structure, offer pathways to control and manipulate matter in previously unattainable ways. Researchers anticipate that a more comprehensive understanding of these effects will enable the design of materials with tailored functionalities – including enhanced energy efficiency, novel sensing capabilities, and improved data storage. Furthermore, harnessing these topological states could be instrumental in building robust quantum bits, or qubits, essential components for realizing the potential of quantum computation and communication, potentially overcoming limitations faced by current quantum technologies and ushering in a new era of technological innovation.

The exploration of magnetoplasma waves within magnetic Weyl semimetals reveals a subtle interplay between material properties and wave propagation-a harmony reminiscent of elegantly tuned systems. This research, focused on topologically protected modes at domain walls, suggests that functionality arises not from complexity, but from a refined understanding of fundamental principles. As Henry David Thoreau observed, “Simplicity, simplicity.” The beauty of these findings lies in how a seemingly simple concept-wave behavior in a novel material-unlocks the potential for sophisticated photonic devices, whispering promises of innovation rather than shouting them from the rooftops. The localization of these modes at domain walls exemplifies how form-the material’s structure-and function-wave propagation-are inextricably linked.

Where the Waves Will Take Us

The demonstration of topologically protected magnetoplasma waves within magnetic Weyl semimetals, particularly those localized at domain walls, feels less like a destination and more like a careful calibration of instruments. The immediate implications for novel photonic devices are, admittedly, appealing – a whisper of potential in a field often characterized by shouting. However, the true challenge lies not in simply building with these waves, but in understanding the subtle interplay between topology, material imperfections, and the inevitable demands of practical application.

Existing work skirts around the question of robustness. How readily do these protected modes degrade under realistic conditions? Domain wall stability, for example, is rarely absolute. Further investigation into the influence of scattering, disorder, and non-linear effects is critical. A truly elegant device will not demand pristine materials or idealized geometries, but will embrace imperfection, turning limitations into features.

Ultimately, the pursuit of these waves is a study in symmetry and its breaking. The aesthetic of the system-the clean lines of topologically protected modes-is a sign of deep understanding. Beauty and consistency will not simply make these systems durable and comprehensible; they will dictate the limits of what is possible. The next phase of research must prioritize not just what these waves can do, but how they do it, with an eye toward the underlying principles that govern their behavior.

Original article: https://arxiv.org/pdf/2601.10014.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/