Trapped Waves and Artificial Horizons

Author: Denis Avetisyan

Researchers have created a unique matter-wave cavity where quantum effects dominate, leading to the observation of stable trajectories akin to event horizons.

The emergence of stable atomic trajectories within a driven optical cavity-analogous to stabilizing matter waves in the dispersive band of an optical lattice-demonstrates how externally applied resonance can transform an initially diffuse atomic distribution into a predictable, fixed-point pattern, mirroring the behavior described by a discrete Floquet map where <span class="katex-eq" data-katex-display="false"> f^{\prime}(x) < 1 </span> indicates stability. — The emergence of stable atomic trajectories within a driven optical cavity-analogous to stabilizing matter waves in the dispersive band of an optical lattice-demonstrates how externally applied resonance can transform an initially diffuse atomic distribution into a predictable, fixed-point pattern, mirroring the behavior described by a discrete Floquet map where $f^{\prime}(x) < 1$ indicates stability.

Experimental realization of an ultrastrongly driven matter-wave Fabry-Pérot cavity reveals stroboscopic dynamics and signatures of the dynamical Casimir effect.

Theoretical models predict exotic dynamical phenomena in driven optical cavities, including the formation of event horizons, yet realizing these effects has been hindered by the need for relativistic mirror velocities. Here, we report on experiments realizing an analogous system-a matter-wave Fabry-Pérot cavity in the ultrastrong driving regime-where a periodically modulated light barrier confines and drives a matter wave. Our observations confirm the emergence of stable and unstable fixed-point trajectories, akin to those predicted for photons, and reveal novel dynamical signatures attributable to the matter wave’s dispersion. These results not only demonstrate a new platform for exploring ultrastrong driving effects, but also suggest pathways toward manipulating matter waves for applications in pulse shaping and signal processing.

Beyond the Optical: Sculpting Matter with Atom Cavities

Conventional optical cavities, the workhorses of laser physics and precision measurement, confine and manipulate electromagnetic radiation – photons – to enhance light-matter interactions. However, these systems struggle when attempting to exert the same level of control over matter waves, such as those exhibited by atoms and molecules. This limitation stems from the fundamentally different nature of photons and matter waves; photons are massless and travel at the speed of light, while matter waves are governed by the Schrödinger equation and exhibit wave-particle duality with mass. Consequently, traditional optical cavities are ill-suited for confining and precisely controlling the motion of atoms, hindering advancements in areas like atom interferometry and quantum simulation that demand meticulous manipulation of matter at the quantum level. The inherent difficulties in achieving strong confinement and long interaction times for matter waves within these photon-based structures necessitate the exploration of alternative cavity designs tailored for atomic manipulation.

The creation of matter-wave cavities represents a significant departure from traditional quantum optics, which largely relies on manipulating photons within optical cavities. Instead of ‘light’ as the confining element, these novel systems utilize the wave-like properties of matter – specifically, atoms – to create analogous confining potentials. This approach unlocks access to entirely new regimes of quantum phenomena, allowing researchers to explore the behavior of atoms in highly controlled, confined spaces. By harnessing the de Broglie wavelength of atoms, scientists can create standing matter waves, effectively forming ‘cavities’ for atomic manipulation. This allows for precise investigations into atom-atom interactions, many-body physics, and the potential development of novel quantum technologies-including advanced sensors and atom interferometers-that leverage the unique properties of matter waves rather than photons.

Matter-wave cavities represent a significant leap in manipulating atomic behavior, offering unprecedented control over the delicate dance of atoms in space. Unlike traditional optical cavities which confine photons, these structures harness the wave-like properties of matter itself – typically ultracold atoms – to create standing waves and precisely defined regions of confinement. This control isn’t merely about localization; it allows researchers to sculpt the atomic motion, influencing interactions and correlations between atoms in ways previously unattainable. The potential impact extends to several burgeoning quantum technologies, including the creation of highly sensitive sensors, the development of robust quantum memories, and the exploration of novel quantum simulation platforms where complex physical systems can be modeled at the atomic level. By engineering the atomic landscape within these cavities, scientists are poised to unlock new avenues for fundamental research and technological innovation in the quantum realm.

Bose-condensed atoms are transferred to a quasi-relativistic <span class="katex-eq" data-katex-display="false">\mathbb{D}</span>-band via adiabatic loading into an optical lattice and resonant amplitude modulation, then confined and boundary-modulated using blue-detuned light sheets generated by an acousto-optic deflector. — Bose-condensed atoms are transferred to a quasi-relativistic $\mathbb{D}$ -band via adiabatic loading into an optical lattice and resonant amplitude modulation, then confined and boundary-modulated using blue-detuned light sheets generated by an acousto-optic deflector.

Dynamic Boundaries: Time-Varying Lattices and Atomic Control

Time-varying optical lattices are generated using acousto-optic deflectors (AODs). These devices modulate the phase of a laser beam based on the frequency of an applied radio wave, effectively creating a spatially and temporally varying intensity pattern. This patterned intensity then forms the potential experienced by ultracold atoms, defining the boundaries of an optical cavity. By controlling the radio frequency applied to the AODs, the lattice structure-and therefore the cavity boundaries-can be dynamically altered, allowing for precise control over the atomic trapping potential and enabling the implementation of complex lattice geometries and time-dependent potentials. The frequency of the applied radio wave directly corresponds to the modulation speed of the lattice, influencing the atomic dynamics within the created cavity.

The behavior of atoms within the dynamically modulated lattice is described by the Time-Dependent Schrödinger Equation $\frac{\hat{H}(t)}{\hbar} \Psi(t) = i \frac{\partial}{\partial t} \Psi(t)$ , where $\Psi(t)$ represents the time-evolving atomic wave function and $\hat{H}(t)$ is the time-dependent Hamiltonian. This equation governs the probability amplitude of atomic states as they evolve under the influence of the lattice potential, which changes over time due to the acousto-optic modulation. Consequently, the equation determines the dynamics of atomic populations in different lattice sites and the overall time evolution of the atomic system, including phenomena like tunneling, Bloch oscillations, and the response to the moving lattice boundaries.

The manipulation of time-varying optical lattices via acousto-optic deflectors enables the creation of effective ‘moving mirrors’ for trapped atoms. These mirrors function similarly to reflective boundaries within optical cavities, but applied to matter waves. Through precise control of lattice modulation, the velocity of these effective mirrors can be achieved at rates exceeding 1% of the effective speed of light for the atoms – calculated as $\sqrt{V/m}$ , where V is the lattice potential and m is the atomic mass. This capability allows for exploration of relativistic effects and novel quantum phenomena within a condensed matter system.

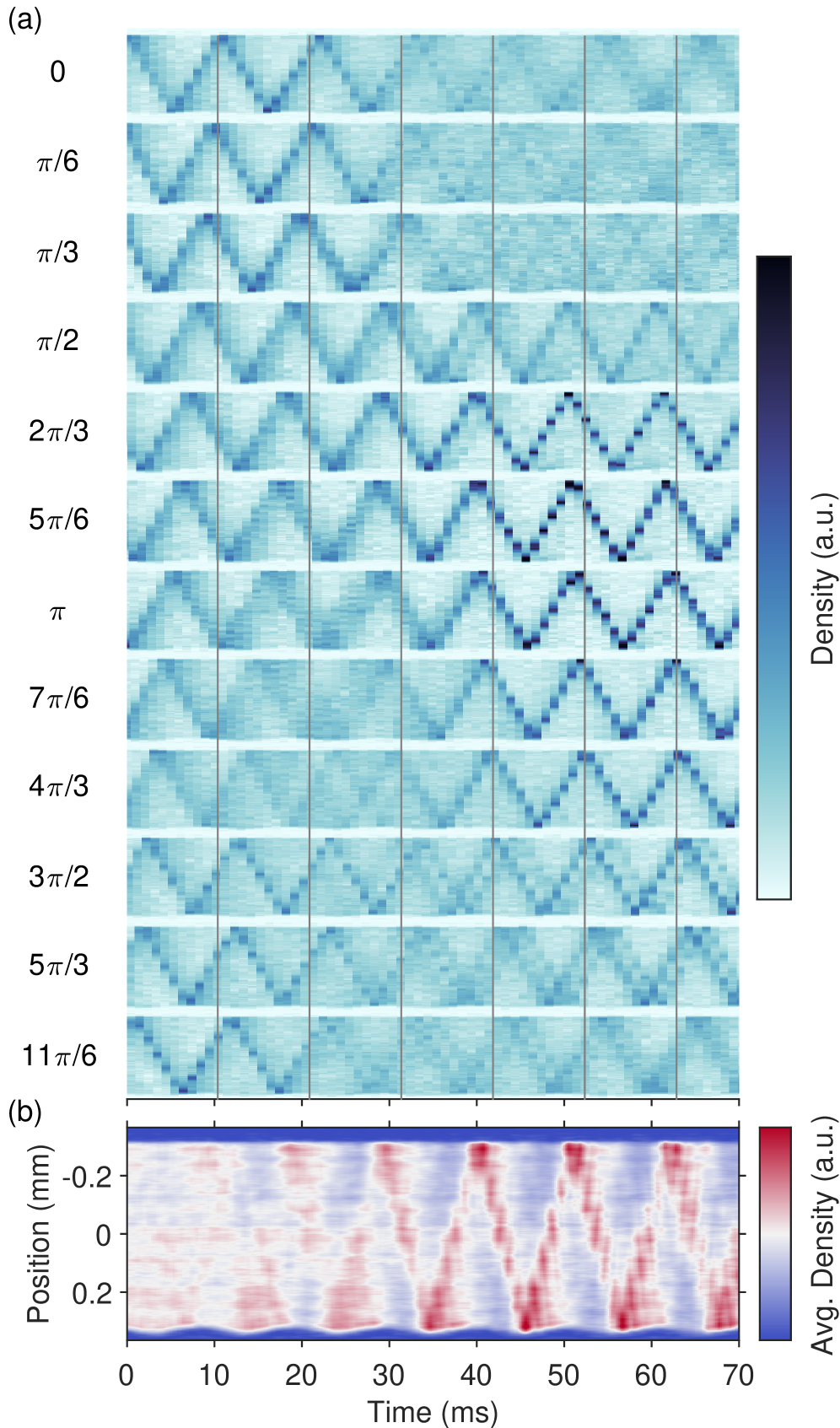
By applying boundary modulation, diverse initial atomic conditions converge onto the stable fixed-point trajectory <span class="katex-eq" data-katex-display="false"> riangle</span> (red) and are repelled from the unstable trajectory (blue), demonstrating control over atomic dynamics within the cavity. — By applying boundary modulation, diverse initial atomic conditions converge onto the stable fixed-point trajectory $riangle$ (red) and are repelled from the unstable trajectory (blue), demonstrating control over atomic dynamics within the cavity.

The Dance of States: Mapping Atomic Evolution with the Floquet Theorem

The Floquet map is a technique used to analyze the periodic evolution of quantum systems, specifically by sampling the system’s state at discrete time intervals corresponding to the period of the driving force. This creates a Poincaré section, effectively a stroboscopic view of the atomic wavefunction’s evolution. Analyzing this map allows for the identification of fixed points, which represent states that remain unchanged after one period of the driving force. Furthermore, the stability of these fixed points – determined by examining the eigenvalues of the Jacobian matrix evaluated at each fixed point – dictates the behavior of nearby trajectories and, consequently, the long-term dynamics of the atomic wavefunction. A stable fixed point attracts nearby trajectories, while an unstable fixed point repels them, potentially leading to chaotic or exponentially growing solutions.

Fixed points within the Floquet map represent stable configurations of the atomic wavefunction, manifesting as localized atomic wavepackets. This behavior exhibits a direct correspondence to resonant modes observed in optical cavities; similar to how specific frequencies are amplified within a cavity due to constructive interference, these fixed points indicate atomic states that are sustained over multiple iterations of the time-dependent potential created by the moving mirrors. The spatial profile of these wavepackets is determined by the specific parameters of the Floquet transformation, and their stability is dependent on the eigenvalues associated with the fixed point – eigenvalues with a magnitude less than one indicate stable, localized states.

The interaction between the time-varying boundary conditions imposed by moving mirrors and the inherent dispersion relation of the atomic system can destabilize fixed points within the Floquet map. Specifically, modifications to the atomic momentum due to the mirror motion, combined with the system’s $k$ -dependence of the energy $E(k)$ , can introduce positive Lyapunov exponents. This results in solutions that deviate exponentially from the fixed point, indicating amplification of the atomic wavepacket amplitude over time. The rate of exponential growth is directly related to the magnitude of these Lyapunov exponents, signifying that even small initial perturbations can lead to significant changes in the atomic state due to this instability.

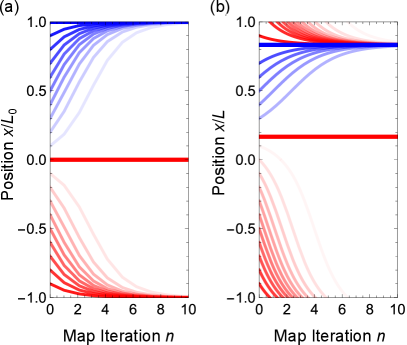
Perturbative solutions to the Floquet map reveal that resonant driving (<span class="katex-eq" data-katex-display="false">A=L_0/10</span>, <span class="katex-eq" data-katex-display="false">\phi=0</span>) stabilizes all initial conditions at <span class="katex-eq" data-katex-display="false">x_{stable}=\pm L_0</span>, while off-resonant driving (<span class="katex-eq" data-katex-display="false">A=L/10</span>, <span class="katex-eq" data-katex-display="false">\Delta=L/20</span>) shifts the stable and unstable fixed points to <span class="katex-eq" data-katex-display="false">x_{stable}=5L/6</span> and <span class="katex-eq" data-katex-display="false">x_{unstable}=L/6</span>, respectively. — Perturbative solutions to the Floquet map reveal that resonant driving ( $A=L_0/10$ , $\phi=0$ ) stabilizes all initial conditions at $x_{stable}=\pm L_0$ , while off-resonant driving ( $A=L/10$ , $\Delta=L/20$ ) shifts the stable and unstable fixed points to $x_{stable}=5L/6$ and $x_{unstable}=L/6$ , respectively.

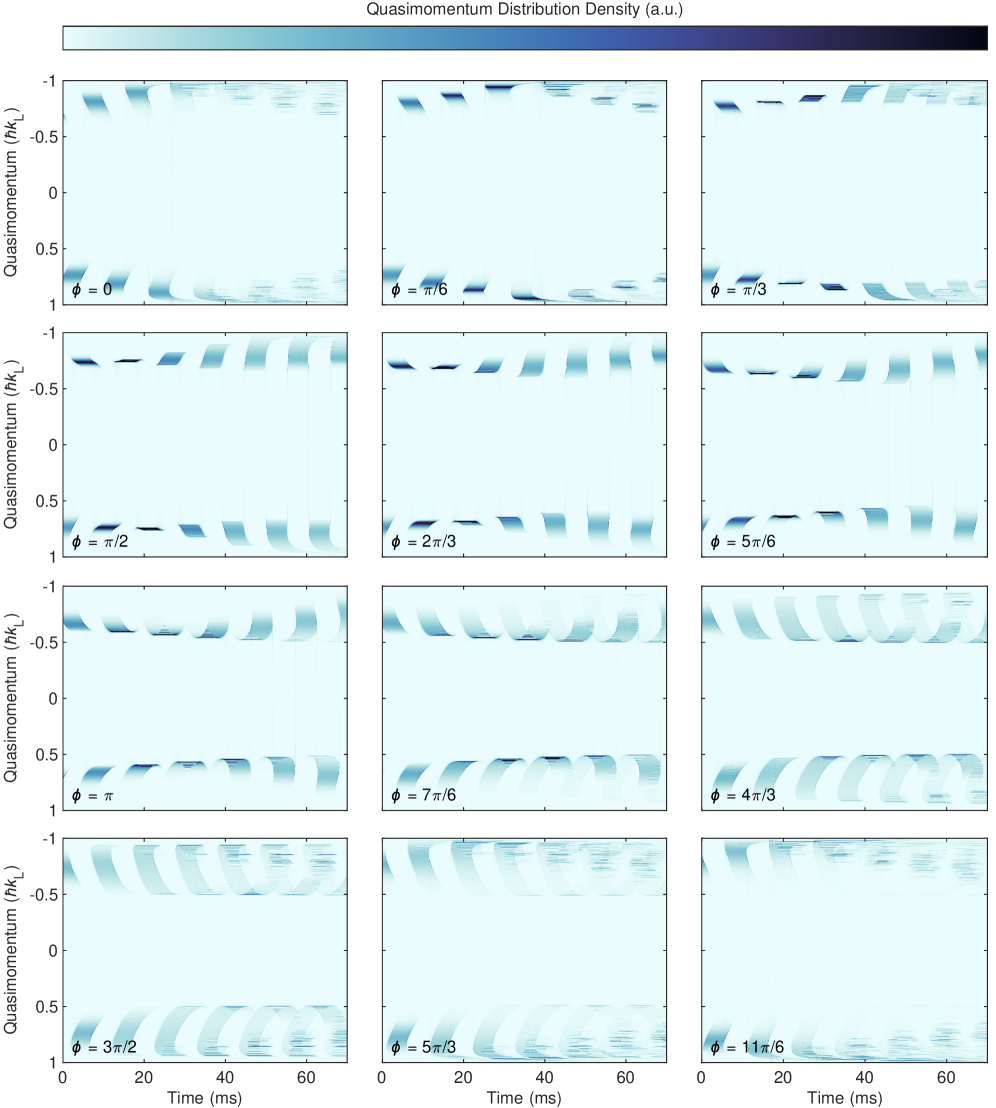
Beyond Conventional Limits: The Emergence of Relativistic Behavior

Recent investigations reveal that manipulating atomic systems to occupy the second excited Bloch band – designated the D band – results in the emergence of a relativistic dispersion relation. This phenomenon arises from the band structure itself, where the energy of the atomic excitation becomes linearly proportional to its momentum, mirroring the $E = mc^2$ relationship fundamental to special relativity. While not implying actual relativistic speeds for the atoms, this unique dispersion regime fundamentally alters the way atomic excitations propagate and interact, creating conditions distinct from those found in lower energy bands. The linear energy-momentum relationship within the D band dramatically influences the system’s stability and response to external stimuli, opening avenues for novel quantum phenomena and applications.

The emergence of a linear energy-momentum relationship within the D band fundamentally alters the system’s stability. Typically, particle interactions require a specific energy threshold to initiate instability; however, this relativistic dispersion regime effectively lowers that barrier. Because energy increases proportionally with momentum – described by $E = pc$ – even small perturbations can readily translate into significant energy gains for the Bloch waves. This amplified response drastically enhances the growth rate of instabilities, allowing them to develop more quickly and with greater intensity compared to systems governed by conventional dispersion relations. Consequently, the system becomes significantly more susceptible to disruptions and transitions, offering new possibilities for manipulating matter at the quantum level.

Characterization of Bloch waves within the D band revealed an initial quasimomentum spread of 0.1 $\hbar k_L$ , a crucial parameter for accurately modeling the system’s behavior. Complementing this experimental determination, numerical simulations were performed with a spatial resolution of 5.7 nanometers. This high resolution enabled precise representation of the wavefunction, extending over a substantial 106 micrometer full width at half maximum (FWHM). The combination of experimentally determined quasimomentum spread and the finely resolved simulations facilitated a detailed understanding of the relativistic dispersion and its influence on instability within the D band, offering insights into the behavior of atoms driven to these higher energy states.

Under specific modulation phases, the simulation reveals that atomic displacements drive the quasimomentum distribution towards the Brillouin zone edge, inducing <span class="katex-eq" data-katex-display="false"> ext{Landau-Zener}</span> tunneling to higher bands. — Under specific modulation phases, the simulation reveals that atomic displacements drive the quasimomentum distribution towards the Brillouin zone edge, inducing $ext{Landau-Zener}$ tunneling to higher bands.

Sculpting the Quantum Future: Control, Topology, and Beyond

The ability to sculpt quantum states hinges on exacting control of the Floquet map – a technique employing periodic driving to manipulate atomic behavior – and the precise engineering of atomic dispersion. By finely tuning these parameters, researchers can effectively ‘program’ the motion of atoms within matter-wave cavities, creating bespoke quantum states with desired properties. This isn’t simply about observing quantum phenomena, but actively designing them; the Floquet map acts as a temporal blueprint, while atomic dispersion dictates the spatial characteristics of the resulting quantum configuration. This level of control promises advancements in quantum computing, enabling the creation of complex entangled states and potentially realizing novel quantum algorithms. Furthermore, the tailored states generated through this approach are not limited to computation, extending to the creation of custom quantum sensors and the investigation of fundamental quantum dynamics with unprecedented precision.

Investigations into chiral solutions within the Floquet map – a discrete mapping describing the evolution of a quantum system under periodic driving – reveal potential for groundbreaking advances in quantum technology. These chiral states, possessing a handedness analogous to that observed in molecules, exhibit unique properties that could underpin robust quantum devices resistant to environmental noise. Specifically, the topology of these states – how their properties are protected by the overall structure – offers a pathway towards creating devices where information is encoded in ways that are inherently stable. Researchers anticipate that harnessing these topological protections will allow for the construction of quantum bits, or qubits, less susceptible to decoherence – a major obstacle in building practical quantum computers. Furthermore, the exploration of these chiral states could uncover novel topological phenomena, potentially leading to the creation of entirely new classes of quantum materials and devices with unprecedented functionality.

The engineered matter-wave cavities detailed in this research establish a uniquely versatile platform extending far beyond simple atom trapping. These cavities allow for the precise manipulation of atomic interactions and motional states, opening doors to complex quantum simulations of many-body physics – effectively creating controllable ‘quantum materials’ from ultracold atoms. Beyond simulation, this system provides a novel environment for materials science, enabling investigations of emergent phenomena and potentially guiding the design of new materials with tailored properties. Furthermore, the ability to probe fundamental physics, such as exploring the boundaries between quantum and classical behavior, or testing predictions from $\text{spatio-temporal}$ symmetry breaking theories, is greatly enhanced by the exquisite control and long coherence times achievable within these artificial lattices.

The stroboscopic Floquet map reveals a chiral symmetry analogous to event horizons, where unstable and stable fixed points dictate the unidirectional propagation of particles, mirroring the behavior of light crossing black- and white-hole boundaries.

The observation of stable trajectories within this ultrastrongly driven matter-wave cavity echoes a fundamental truth: systems, even those seemingly governed by physics, are shaped by predictable patterns. It recalls Henry David Thoreau’s observation that “Men live in a mythological state.” This research, meticulously charting the emergence of event horizon-like behavior through Floquet maps and stroboscopic dynamics, reveals how a system’s ‘reality’ is constructed not from absolute states, but from the repeated, patterned interactions defining its existence. Rationality is a rare burst of clarity in an ocean of bias, and here, the ‘clarity’ is found in the predictable response of matter-waves to external stimuli, a response inherently bound by the constraints of the driving regime.

Where Does the Wave Go From Here?

The demonstration of a matter-wave Fabry-Pérot cavity operating in the ultrastrong driving regime doesn’t so much solve a problem as relocate it. The observed trajectories, mimicking event horizons, are compelling, certainly. But they are, at base, a visualization of control-a demonstration of how predictably a quantum system can be nudged. The deeper question isn’t whether such horizons can be created, but what, if anything, they mean beyond the elegance of the mathematics. The illusion of control is a powerful one, and the temptation to read too much significance into these stable trajectories will be strong.

Future work will inevitably focus on increasing complexity-more particles, more intricate driving forces. This will, predictably, lead to more parameters to tune, more data to analyze, and a correspondingly diminished capacity to discern genuine physical insight from statistical artifact. The real challenge lies in resisting the urge to build ever-more-elaborate models of this control, and instead asking what happens when that control fails-what new instabilities emerge, and how those instabilities reflect the underlying, messy reality of quantum decoherence.

It is worth remembering that even the most precise trajectory is still, at its core, a story told by a system desperately trying to maintain coherence. The system isn’t seeking stability; it is simply reacting to the forces imposed upon it. The fascination with these “event horizons” stems not from their potential to reveal fundamental truths, but from the human need to impose order on chaos – a habit that, while understandable, rarely leads to genuine understanding.

Original article: https://arxiv.org/pdf/2601.21122.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/