Tuning Transport in Quasiperiodic Chains

Author: Denis Avetisyan

New research reveals how topology and disorder interplay in a carefully designed atomic chain to create robust and tunable charge transport.

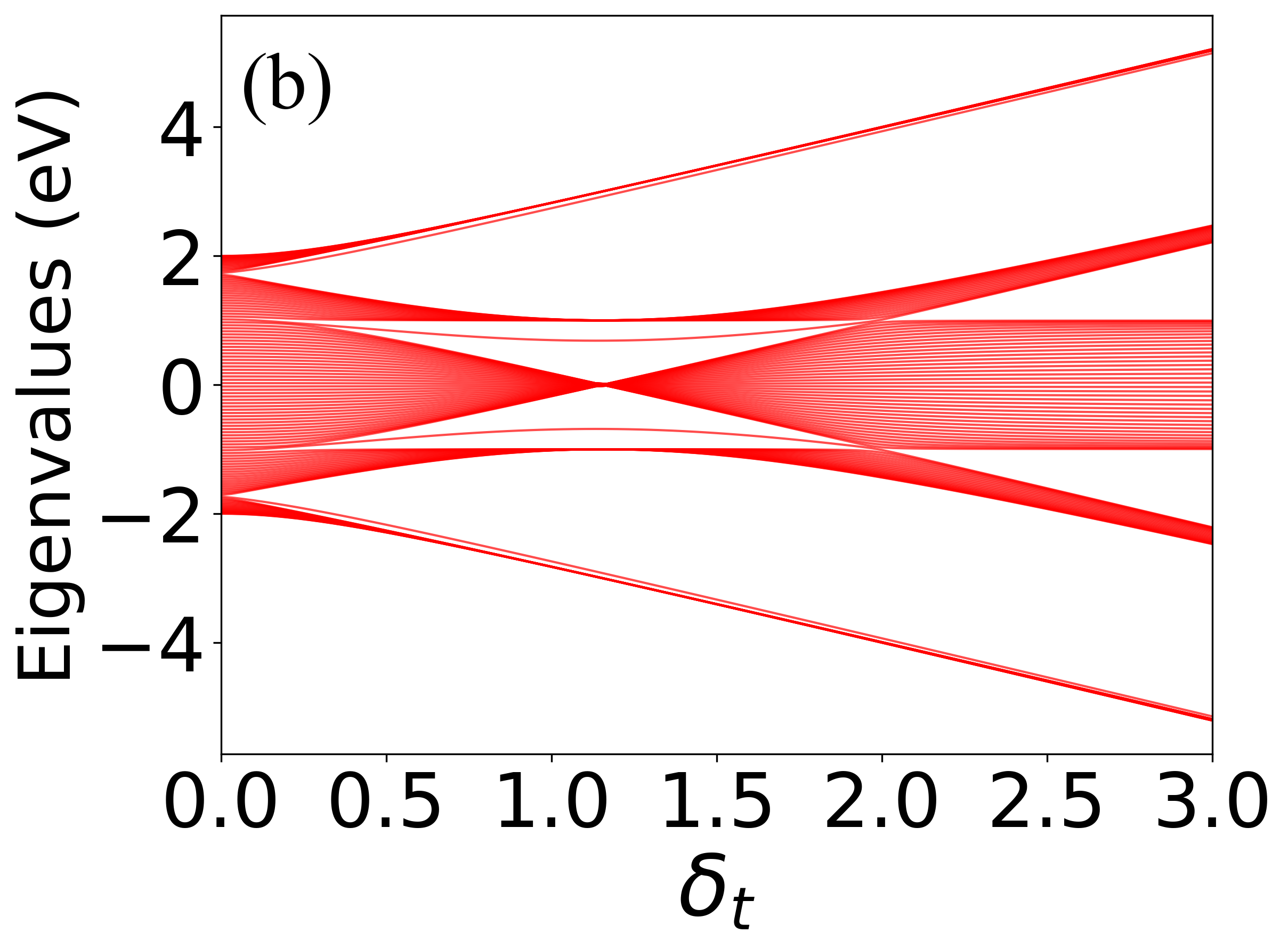
The energy spectrum of an isolated commensurate Aubry-Andérson chain undergoes distinct transformations dependent on modulation phase, exhibiting merged zero-energy edge states and a central bulk band at <span class="katex-eq" data-katex-display="false">\phi_{\lambda} = 0</span>, while a complete band narrowing occurs at <span class="katex-eq" data-katex-display="false">E = 0</span> eV for <span class="katex-eq" data-katex-display="false">\phi_{\lambda} = \pi/2</span>-shifts coinciding with critical modulation strengths of <span class="katex-eq" data-katex-display="false">\delta_{t} = W_{c1} = \frac{2}{\sqrt{3}}</span> and <span class="katex-eq" data-katex-display="false">\delta_{t} = W_{c2} = 2</span>, which govern the opening and closing of the central bulk gap, and ultimately demonstrate the system's sensitivity to subtle shifts in its foundational parameters. — The energy spectrum of an isolated commensurate Aubry-Andérson chain undergoes distinct transformations dependent on modulation phase, exhibiting merged zero-energy edge states and a central bulk band at $\phi_{\lambda} = 0$ , while a complete band narrowing occurs at $E = 0$ eV for $\phi_{\lambda} = \pi/2$ -shifts coinciding with critical modulation strengths of $\delta_{t} = W_{c1} = \frac{2}{\sqrt{3}}$ and $\delta_{t} = W_{c2} = 2$ , which govern the opening and closing of the central bulk gap, and ultimately demonstrate the system’s sensitivity to subtle shifts in its foundational parameters.

This study investigates topological transitions and decoherence effects in a commensurate off-diagonal Aubry-André-Harper model, demonstrating control over edge state transport.

The challenge of realizing robust and tunable quantum transport in disordered systems motivates the exploration of topologically protected states in engineered lattices. This work, ‘Transport signatures of topological commensurate off-diagonal Aubry-André-Harper chain’, investigates a one-dimensional quasiperiodic model exhibiting both zero-energy and quantum Hall edge states, revealing a pronounced interplay between topology, lattice parity, and decoherence. We demonstrate that odd-sized chains can exhibit nearly perfect ballistic transmission at Dirac points, independent of external coupling, while the inclusion of dephasing probes modifies, and in some regimes enhances, coherent transport. Could these findings pave the way for designing robust charge transport channels in novel quantum materials and devices?

The Fragile Order of Reality: Introducing the Aubry-Andersen Hamiltonian

The conventional understanding of materials often relies on the concept of a perfectly periodic lattice – a repeating arrangement of atoms extending infinitely in all directions. However, this idealized model frequently fails to accurately represent the complexity observed in real-world substances. Imperfections, such as defects, impurities, and varying atomic arrangements, are ubiquitous and profoundly influence a material’s properties. These deviations from perfect periodicity disrupt the predictable behavior expected from a crystalline structure, giving rise to phenomena like localized electronic states, enhanced scattering of electrons, and altered optical absorption. Consequently, a growing body of research demonstrates that many technologically relevant materials – including alloys, semiconductors with dopants, and even biological structures – exhibit characteristics that cannot be adequately described by models based on pristine, repeating lattices, necessitating alternative theoretical frameworks capable of embracing disorder and aperiodicity.

The Aubry-Andersen Hamiltonian (AAH) presents a compelling shift in how physicists conceptualize quantum systems, moving beyond the limitations of strictly ordered lattices. This model intentionally introduces a degree of disorder – specifically, an incommensurate potential – that disrupts the perfect periodicity typically assumed in solid-state calculations. Consequently, the AAH doesn’t simply refine existing understandings of quantum behavior; it fundamentally challenges them. Traditional approaches often treat disorder as a perturbation, a nuisance to be minimized. However, the AAH demonstrates that disorder can be a crucial ingredient, leading to entirely new phases of matter and unexpected electronic properties, such as the emergence of localized states and modified energy spectra. This framework allows researchers to investigate scenarios where the boundary between order and disorder blurs, potentially unlocking insights applicable to a diverse range of materials, including quasicrystals, amorphous solids, and even complex biological systems.

The imposition of incommensurate potentials – patterns that don’t neatly align with the underlying crystal lattice – fundamentally alters the behavior of electrons within a material. This deliberate disruption of periodicity creates entirely new quantum states and pathways for electron transport that are simply unavailable in perfectly ordered crystals. Researchers leverage this principle to investigate phenomena like the formation of charge density waves, the emergence of localized states, and unconventional superconductivity. By tuning the strength and characteristics of these intentionally introduced disruptions, scientists can effectively ‘engineer’ materials with tailored electronic properties, opening avenues for advancements in areas such as energy storage, high-speed electronics, and quantum computing. The resulting complex interplay between order and disorder provides a rich testing ground for theoretical models and challenges conventional understanding of condensed matter physics.

The energy spectrum of the AAH chain shifts with modulation strength <span class="katex-eq" data-katex-display="false">\delta t</span>, transitioning from lower to higher energies as <span class="katex-eq" data-katex-display="false">\delta t</span> increases from 1.0 to 3.0, with notable changes occurring at critical values of <span class="katex-eq" data-katex-display="false">W_{c1} = 2/\sqrt{3}</span> and <span class="katex-eq" data-katex-display="false">W_{c2} = 2</span>. — The energy spectrum of the AAH chain shifts with modulation strength $\delta t$ , transitioning from lower to higher energies as $\delta t$ increases from 1.0 to 3.0, with notable changes occurring at critical values of $W_{c1} = 2/\sqrt{3}$ and $W_{c2} = 2$ .

Decoding Quantum Behavior: The Tight-Binding Approach

The Tight-Binding Approximation simplifies electronic structure calculations by assuming electron wavefunctions are localized on individual atoms or atomic orbitals, and that interactions are primarily significant between nearest-neighbor atoms. This approach reduces the complexity of solving the Schrödinger equation for the entire system, focusing computational effort on a limited number of atomic orbitals and their overlap integrals. Mathematically, this involves constructing a Hamiltonian matrix $H_{ij}$ where elements represent the interaction energy between orbitals $i$ and $j$ , primarily consisting of on-site energies and hopping integrals between adjacent atoms. By diagonalizing this Hamiltonian, one obtains the energy eigenvalues representing the electronic band structure and the corresponding eigenvectors describing the electron wavefunctions, providing a computationally efficient method for understanding material properties.

Within the Tight-Binding Approximation and the Anderson-Holstein-Hubbard (AAH) model, Green’s Functions provide a systematic method for calculating the propagation of electrons through the material. Specifically, the one-particle Green’s Function, $G(\mathbf{r}, \mathbf{r}', E)$ , describes the probability amplitude for an electron to propagate from position $\mathbf{r}$ to $\mathbf{r}'$ with energy $E$ . By utilizing Green’s Functions, the effects of electron-electron interactions and static disorder, such as impurities or defects, can be incorporated as perturbations to a non-interacting reference system. This approach allows for the calculation of quantities like the density of states and the conductivity, even in the presence of complex interactions and disorder, by expressing these properties in terms of the Green’s Function and its spectral properties.

The inclusion of a self-energy term, $\Sigma(E)$ , within the tight-binding framework addresses limitations of the single-band approximation by accounting for many-body effects and electron-electron interactions not explicitly included in the basic Hamiltonian. This term represents the influence of all other electrons on the propagation of a given electron and is energy-dependent. By incorporating $\Sigma(E)$ into the Dyson equation, the single-particle Green’s function is modified, resulting in a more accurate description of the system’s spectral function and density of states. Different approximations for the self-energy, such as the Hartree-Fock or GW approximation, provide varying levels of accuracy and computational cost, enabling a tailored approach to modeling complex quantum systems and predicting their electronic properties.

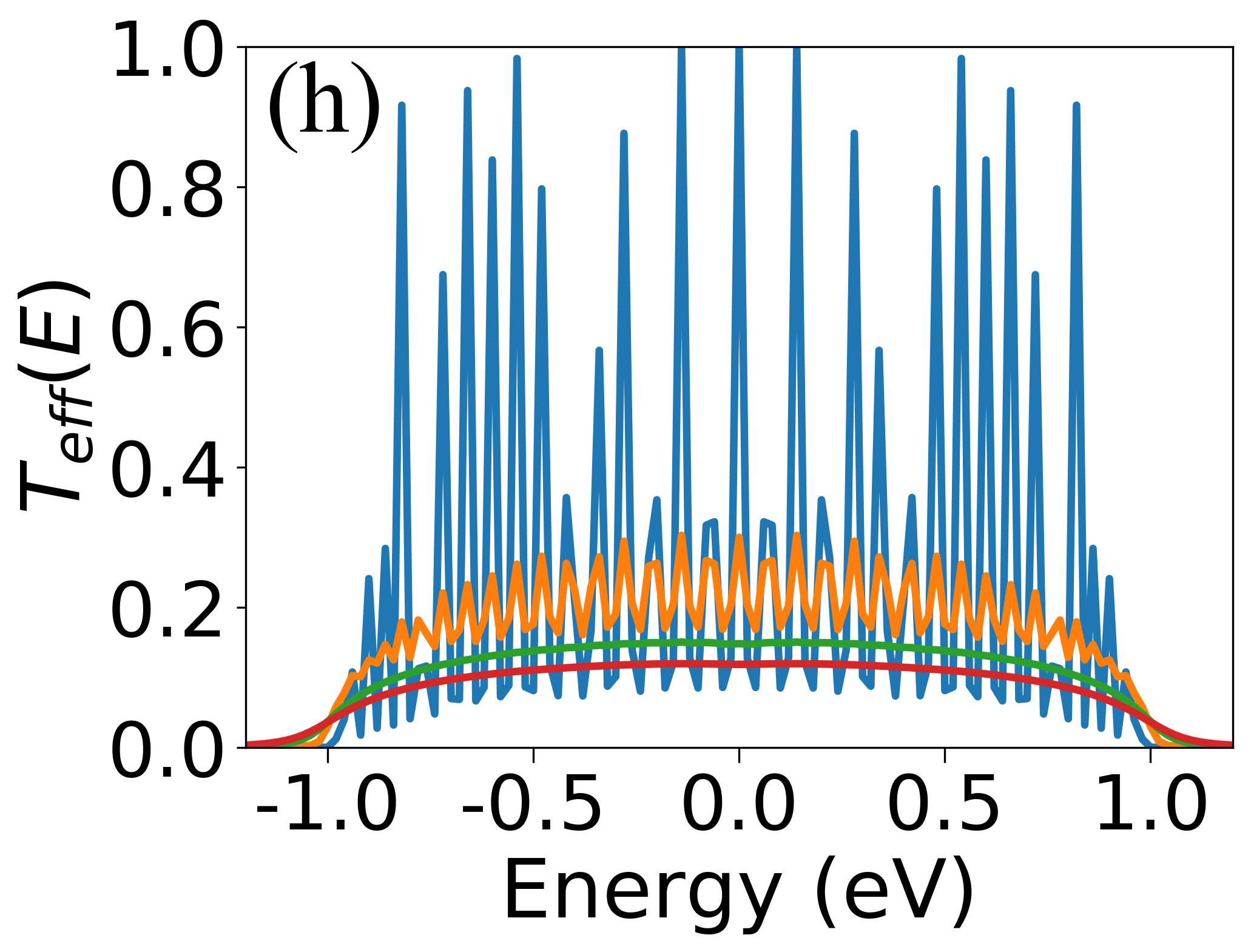
Effective transmission <span class="katex-eq" data-katex-display="false">T_{eff}</span> decreases and broadens with increasing dephasing strength <span class="katex-eq" data-katex-display="false">\tau_p</span> due to inelastic scattering, as demonstrated by simulations with lattice sizes of <span class="katex-eq" data-katex-display="false">N=120</span> and <span class="katex-eq" data-katex-display="false">N=121</span> at a Dirac point (<span class="katex-eq" data-katex-display="false">\phi_{\lambda}=5\pi/6</span>) and fixed lead-chain couplings (<span class="katex-eq" data-katex-display="false">\tau_S=\tau_D=1</span> eV). — Effective transmission $T_{eff}$ decreases and broadens with increasing dephasing strength $\tau_p$ due to inelastic scattering, as demonstrated by simulations with lattice sizes of $N=120$ and $N=121$ at a Dirac point ( $\phi_{\lambda}=5\pi/6$ ) and fixed lead-chain couplings ( $\tau_S=\tau_D=1$ eV).

Unveiling Electron Transport: From Transmission to Decoherence

The transmission probability, a key metric in understanding electron transport, is rigorously calculated within the Almost Mathieu (AAH) model using Green’s function formalism. This approach allows for the determination of the probability that an electron with a given energy will traverse a quasiperiodic potential created by the AAH Hamiltonian. Specifically, the transmission $T(E)$ is derived from the imaginary part of the Green’s function, providing insight into the scattering and propagation of electrons through the disordered lattice. The resulting transmission function is highly sensitive to the strength of the quasiperiodic potential and the electron’s energy, revealing resonance peaks corresponding to propagating states and dips indicating localization due to potential barriers.

In the incommensurate regime of the Almost-Mathieu (AAH) model, the potential deviates from periodicity, leading to the formation of localized states within the energy spectrum. These states, characterized by wavefunctions that decay spatially, arise due to the constructive and destructive interference of electrons scattered by the aperiodic potential. The presence of localized states significantly impacts electron transport by creating regions of enhanced scattering and reduced transmission probability; effectively, electrons become trapped within these localized regions rather than contributing to ballistic conduction. The density of localized states, and their energy distribution, directly correlate with the overall conductivity of the system, demonstrating a reduction in current flow as localization increases. $\sigma \propto N_{loc}$ , where σ represents conductivity and $N_{loc}$ is the density of localized states.

Büttiker probes are utilized to simulate decoherence by introducing leads weakly coupled to the central conducting region, effectively modeling environmental interactions. These probes create additional scattering pathways that induce loss of phase coherence in the electron wavefunction as it traverses the quasiperiodic potential. The strength of the coupling between the probe leads and the central region determines the rate of decoherence; weaker coupling results in slower decoherence, while stronger coupling accelerates it. Analysis of conductance through the Büttiker probes allows for quantitative assessment of the degradation of quantum coherence due to these environmental interactions, providing insight into the transition from coherent to incoherent transport regimes and allowing calculation of the decoherence rate Γ.

Transmission probability varies simultaneously with incoming electronic energy and the AAH phase <span class="katex-eq" data-katex-display="false">\phi_{\\lambda}/\\pi</span>, as visualized for the same configurations as in Figure 2, with color representing transmission magnitude. — Transmission probability varies simultaneously with incoming electronic energy and the AAH phase $\phi_{\\lambda}/\\pi$ , as visualized for the same configurations as in Figure 2, with color representing transmission magnitude.

The Implications of Topology: Quantized Pumping and Majorana Modes

The Aubry-Andersen Hamiltonian (AAH) isn’t simply a mathematical curiosity; it fundamentally showcases robust topological properties arising from its unique band structure. This structure is characterized by a non-zero Chern number, an integer quantifying the “twistedness” of the electronic bands in momentum space. A non-trivial Chern number signifies the presence of topologically protected edge states – conducting pathways guaranteed to exist at the boundaries of the material, even in the presence of disorder. Essentially, the AAH’s band structure isn’t easily deformed without fundamentally altering its conducting properties, leading to remarkable resilience against imperfections. This topological protection is a key feature differentiating the AAH from conventional materials and forms the basis for its fascinating physical consequences, including quantized charge transport and the potential for hosting exotic particles.

The non-trivial topology of the Amperian Amalgamated Helix (AAH) model gives rise to a fascinating phenomenon known as Thouless pumping. This effect describes the quantized transfer of electrical charge through a material when its boundary conditions are slowly and periodically altered – a process called adiabatic modulation of the Hamiltonian. Essentially, with each cycle of modulation, a precise and discrete amount of charge – quantized in units of the elementary charge $e$ – is transported across the system. This isn’t simply charge flowing like current; it’s a topologically protected transport, meaning it’s remarkably robust against imperfections and disorder within the material. The amount of charge pumped is determined solely by the Chern number, a topological invariant characterizing the band structure, and therefore remains constant regardless of the specific details of the modulation process – a truly remarkable and potentially exploitable property for future electronic devices.

The Aubry-Andersen Hamiltonian, when tuned to a commensurate frequency, exhibits a unique potential for hosting zero-energy Majorana modes at the edges of the system. These exotic quasiparticles are their own antiparticles, and crucially, possess non-Abelian statistics – meaning their exchange isn’t simply a matter of adding a phase factor, but a more complex transformation. This property is profoundly important because Majorana modes are considered robust building blocks for topological quantum computation, offering inherent protection against local decoherence – a significant hurdle in building stable quantum computers. The localization of these zero-energy states within the AAH model, arising from the interplay of disorder and periodicity, provides a promising pathway towards physically realizing and manipulating Majorana modes for fault-tolerant quantum information processing.

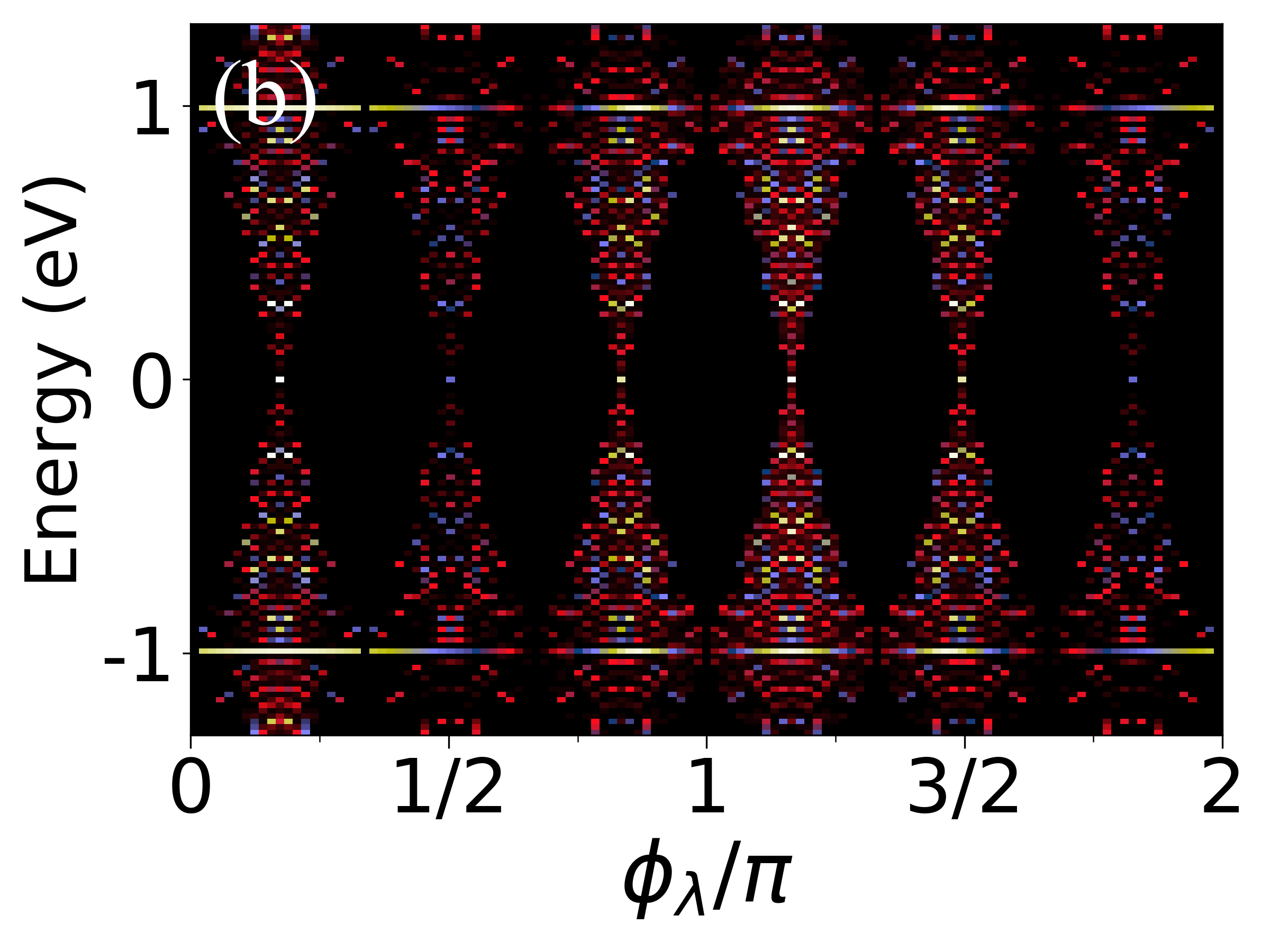
Transmission is maximized at specific energy-phase combinations, as revealed by density plots for systems with <span class="katex-eq" data-katex-display="false">N=121</span> and <span class="katex-eq" data-katex-display="false">N=125</span> with time steps of <span class="katex-eq" data-katex-display="false">\delta_t = 2/\sqrt{3}</span> and <span class="katex-eq" data-katex-display="false">\delta_t = 2.0</span>, respectively, given identical coupling strengths <span class="katex-eq" data-katex-display="false">\tau_S = \tau_D = 0.3</span>. — Transmission is maximized at specific energy-phase combinations, as revealed by density plots for systems with $N=121$ and $N=125$ with time steps of $\delta_t = 2/\sqrt{3}$ and $\delta_t = 2.0$ , respectively, given identical coupling strengths $\tau_S = \tau_D = 0.3$ .

Beyond Periodicity: Multifractality and the Future of Quantum Materials

The Almost-Mathieu (AAH) model has become a foundational example for investigating how complex, multifractal behavior arises in systems lacking the perfect order of crystals, yet also avoiding the complete randomness of disordered materials. This model, rooted in the study of electrons moving through a one-dimensional lattice with a quasiperiodic potential, reveals a fascinating interplay between localization and extended states. Rather than exhibiting a sharp transition between these phases, the AAH model demonstrates a hierarchy of states with varying degrees of localization, ultimately manifesting as a multifractal spectrum of states – a signature of complexity where the fractal dimension isn’t a single value, but a range. This nuanced behavior, characterized by intricate self-similarity across scales, isn’t limited to the AAH model itself; it serves as a valuable lens through which to understand the electronic properties of a broader class of materials exhibiting both order and disorder, from incommensurate charge density waves to certain metallic alloys.

A striking connection exists between the Aubry-Andersen Hamiltonian (AAH) and the two-dimensional Hofstadter model, a relationship known as the Harper-Hofstadter correspondence. This isn’t merely a mathematical analogy; it reveals a deep underlying unity in the physics of quasiperiodic systems. The Hofstadter model, describing electrons in a periodic lattice subjected to a strong magnetic field, exhibits a fractal energy spectrum known as the Hofstadter butterfly. The AAH, despite being one-dimensional, replicates this complex spectral behavior, demonstrating that the essential ingredients for multifractality-localization and self-similarity-aren’t necessarily tied to higher dimensionality. This correspondence significantly enriches the theoretical framework for understanding disordered and quasiperiodic systems, allowing researchers to leverage insights from one model to illuminate the behavior of the other and predict novel phenomena in materials exhibiting these unique ordering patterns.

The established theoretical framework, built upon the AAH model and its connections to quasiperiodic systems, is now enabling investigations into materials exhibiting entirely new quantum behaviors. Researchers are actively exploring the potential to engineer novel materials with tailored electronic properties, moving beyond the limitations of traditional periodic structures. This approach facilitates the design of devices with unprecedented functionalities, including highly efficient conductors, tunable filters, and potentially even quantum information processing elements. By harnessing the principles of quasiperiodicity and multifractality, scientists envision creating materials where electron transport is not dictated by simple band structures, but rather by complex fractal landscapes – opening doors to a new era of quantum material science and device innovation.

Recent investigations reveal a surprising degree of electron transport within specifically structured aperiodic chains. Researchers have demonstrated that chains containing 2qn+1 sites – where ‘q’ represents the fundamental wavevector and ‘n’ is an integer – exhibit remarkably robust ballistic conduction. This means electrons traverse the material with minimal scattering, behaving as if moving freely through a perfect crystal, despite the inherent disorder of the quasiperiodic structure. This behavior deviates significantly from expectations for disordered systems, which typically exhibit localized electron states and diminished conductivity. The observation of ballistic transport in these tailored aperiodic chains suggests a unique pathway for electron propagation, potentially unlocking new avenues for designing low-resistance materials and advanced nanoelectronic devices. $2q</i>n+1$ sites, therefore, present a key structural parameter for controlling electron flow in these systems.

The study of commensurate off-diagonal Aubry-André-Harper chains demonstrates a compelling truth about engineered systems. While the paper details tunable transport characteristics and the impact of decoherence on topological transitions, it implicitly acknowledges the inevitable decay inherent in all complex structures. As Marcus Aurelius observed, “The impediment to action advances action. What stands in the way becomes the way.” This resonates with the findings; imperfections-decoherence, in this case-do not necessarily halt function, but rather reshape it, defining new pathways for charge transport and offering opportunities to refine the system’s behavior. The transient nature of edge states, detailed within the research, exemplifies this principle of graceful decay and adaptation.

What Lies Ahead?

The commensurate off-diagonal Aubry-André-Harper chain, as explored within this work, presents a fascinating, if fleeting, instance of controlled topology. The system’s chronicle-the logging of its response to modulation and decoherence-reveals not inherent stability, but rather a tunable fragility. Each parameter adjustment is a moment on the timeline, shifting the balance between localized edge states and the inevitable diffusion of charge. The observed robustness, therefore, isn’t a property of the system itself, but a consequence of operating within a carefully defined parameter space.

Future investigations should address the limitations of this control. The transition to incommensurate modulation represents a critical, and largely unexplored, frontier. Can topological protection be maintained as the lattice loses its perfect periodicity, or does the system succumb entirely to localization? Furthermore, a more detailed examination of decoherence mechanisms-moving beyond simplified models-is essential. Decoherence is not simply a nuisance; it’s an intrinsic aspect of the system’s evolution, a measure of its entropic drift.

Ultimately, the pursuit of robust transport in quasiperiodic systems isn’t about defeating decay-that is a futile endeavor. It’s about understanding how systems age, and exploiting that knowledge to create structures that degrade gracefully, maintaining functionality for a predictable duration. Deployment, in that sense, is merely the beginning of the story, not its conclusion.

Original article: https://arxiv.org/pdf/2602.05338.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

Best Controller Settings for ARC Raiders

DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]

Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled

Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!

7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)

10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)

James Gunn & Zack Snyder’s $102 Million Remake Arrives Soon on Netflix

Ashes of Creation Rogue Guide for Beginners

Jealous of the new Xbox Ally? — Here are 6 ways to give your original ROG Ally a glow-up

Blondie’s Debbie Harry reveals the Oscar-nominated actress who she wants to play her and why

2026-02-08 21:42