Uncovering Hidden Order: AI Spots Phase Transitions in Complex Systems

Author: Denis Avetisyan

A new machine learning framework autonomously identifies critical points and exotic behavior in both classical and quantum materials, offering a powerful tool for materials discovery and fundamental physics research.

As system size increases from <span class="katex-eq" data-katex-display="false">L=8</span> to <span class="katex-eq" data-katex-display="false">L=14</span>, latent variance exhibits sharpening peaks approaching a critical value of <span class="katex-eq" data-katex-display="false">h_c=1</span>, a behavior consistent with quantum finite-size scaling and indicative of a quantum critical region mirroring the diverging susceptibility observed in classical systems. — As system size increases from $L=8$ to $L=14$ , latent variance exhibits sharpening peaks approaching a critical value of $h_c=1$ , a behavior consistent with quantum finite-size scaling and indicative of a quantum critical region mirroring the diverging susceptibility observed in classical systems.

This work presents a variational autoencoder-based approach for unsupervised discovery of phase transitions, order parameters, and critical behavior in three-dimensional classical and quantum systems, including identifying activated scaling without prior knowledge.

Identifying and characterizing phase transitions-critical points where materials undergo dramatic changes-remains a significant challenge in condensed matter physics, particularly in complex, high-dimensional systems. This research, detailed in ‘From Classical to Quantum: Extending Prometheus for Unsupervised Discovery of Phase Transitions in Three Dimensions and Quantum Systems’, introduces a fully unsupervised machine learning framework-based on variational autoencoders-capable of accurately detecting these transitions and extracting critical exponents in both classical and quantum regimes. Demonstrating robust performance on the 3D Ising model and the transverse field Ising model-even identifying exotic infinite-randomness criticality-this approach generalizes across fundamentally different physical domains without analytical guidance. Could this framework unlock a new era of data-driven discovery in unexplored phase diagrams and complex materials?

Unveiling the Hidden Order Within Complexity

The accurate determination of phase transitions – those pivotal shifts in a system’s physical properties – is fundamental to comprehending the behavior of incredibly diverse phenomena, from the magnetism of novel materials to the dynamics of biological networks. However, real-world data is rarely pristine; inherent noise and incomplete observations frequently obscure the subtle signatures that indicate a transition is occurring. Traditional analytical techniques, reliant on precise measurements and clear order parameters, can falter when confronted with such imperfections, leading to misidentification or complete failure to detect crucial changes in state. This limitation poses a significant challenge across numerous scientific disciplines, necessitating the development of more resilient methods capable of discerning order from chaos and unlocking a deeper understanding of complex systems operating under imperfect conditions.

The inability to reliably detect phase transitions presents a significant obstacle across diverse scientific disciplines. In materials science, characterizing subtle shifts in crystalline structure-vital for designing novel alloys and semiconductors-becomes exceedingly difficult with imperfect data. Similarly, quantum physicists exploring exotic states of matter rely on identifying these transitions to confirm theoretical predictions and unlock new technologies; incomplete or noisy measurements can obscure critical phenomena, leading to misinterpretations of quantum behavior. This pervasive challenge fuels an urgent need for analytical tools capable of discerning genuine phase transitions from background noise, tools that can extract meaningful insights even from compromised datasets and ultimately accelerate discovery in both fundamental research and applied innovation.

The Q-VAE latent space for the TFIM model exhibits clear phase separation based on field strength-from ferromagnetic (blue) to paramagnetic (red)-driven by quantum fluctuations, with the leading latent dimension strongly correlating with <span class="katex-eq" data-katex-display="false">\langle\sigma^{z}\rangle</span> (r=0.97). — The Q-VAE latent space for the TFIM model exhibits clear phase separation based on field strength-from ferromagnetic (blue) to paramagnetic (red)-driven by quantum fluctuations, with the leading latent dimension strongly correlating with $\langle\sigma^{z}\rangle$ (r=0.97).

A Framework for Deciphering System States

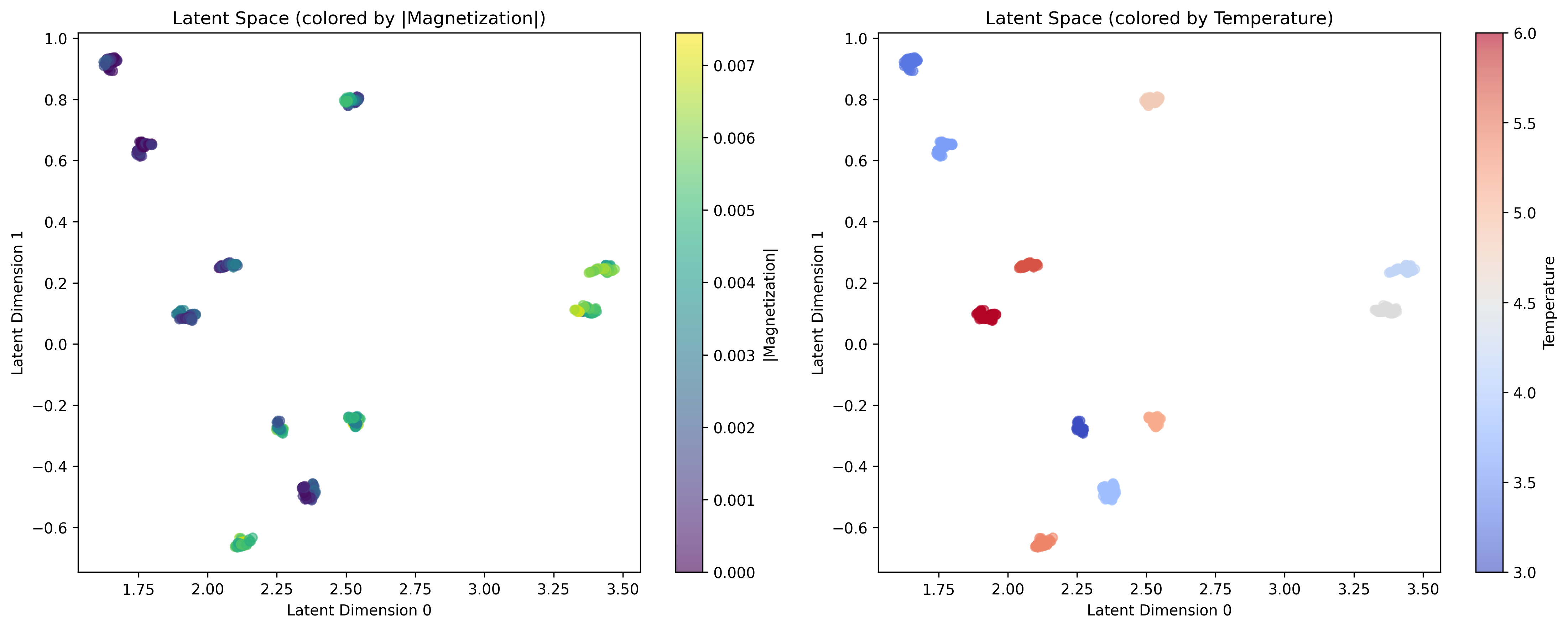
The Prometheus Framework utilizes a Variational Autoencoder (VAE) to create a compressed, latent representation of system states. This process involves encoding high-dimensional system data into a lower-dimensional latent space, and subsequently decoding it to reconstruct the original data. The VAE’s architecture, incorporating probabilistic encoding, allows it to effectively filter noise and identify the underlying, meaningful order present in the system’s state data. By learning this latent representation, the framework can distill complex system behavior into a manageable set of variables, facilitating the analysis of system dynamics and the detection of subtle changes in state without requiring explicit noise reduction techniques.

The Prometheus Framework utilizes unsupervised learning techniques to determine key order parameters and critical exponents directly from system state data, circumventing the need for a predefined Hamiltonian. This is achieved by training a Variational Autoencoder (VAE) on observed system states; the latent space representation learned by the VAE effectively captures the essential degrees of freedom governing the system’s behavior. Analysis of the learned latent space then reveals the order parameters, which characterize the system’s state, and allows for the estimation of critical exponents – values that describe the behavior of the system near phase transitions – without requiring any prior knowledge of the system’s underlying energy function or equations of motion. This approach enables the characterization of complex systems where the Hamiltonian is unknown or intractable.

The Prometheus Framework utilizes a Fidelity-Based Loss function to improve the accuracy of its learned representations of quantum systems. This loss function quantifies the dissimilarity between probability distributions, specifically focusing on the overlap of wavefunctions. By minimizing this difference, the framework ensures that the learned latent space accurately reflects the quantum structure of the system, even in the presence of noise. This is crucial for identifying subtle phase transitions, as these transitions often manifest as minor changes in the system’s wavefunction, which would otherwise be obscured by noise or imperfect modeling. The Fidelity-Based Loss thereby enables the detection of critical phenomena with higher sensitivity than traditional methods reliant on order parameter measurements alone.

Increasing disorder strength in the <span class="katex-eq" data-katex-display="false">Q</span>-VAE latent space transitions the system from sharp phase separation at low disorder to a broadened state, significant smearing with Griffiths tails, and ultimately a broad, irreversible first-passage percolation (IRFP) regime, as indicated by color-coded field strength from ferromagnetic (blue) to paramagnetic (red). — Increasing disorder strength in the $Q$ -VAE latent space transitions the system from sharp phase separation at low disorder to a broadened state, significant smearing with Griffiths tails, and ultimately a broad, irreversible first-passage percolation (IRFP) regime, as indicated by color-coded field strength from ferromagnetic (blue) to paramagnetic (red).

Validating the Framework Through Rigorous Testing

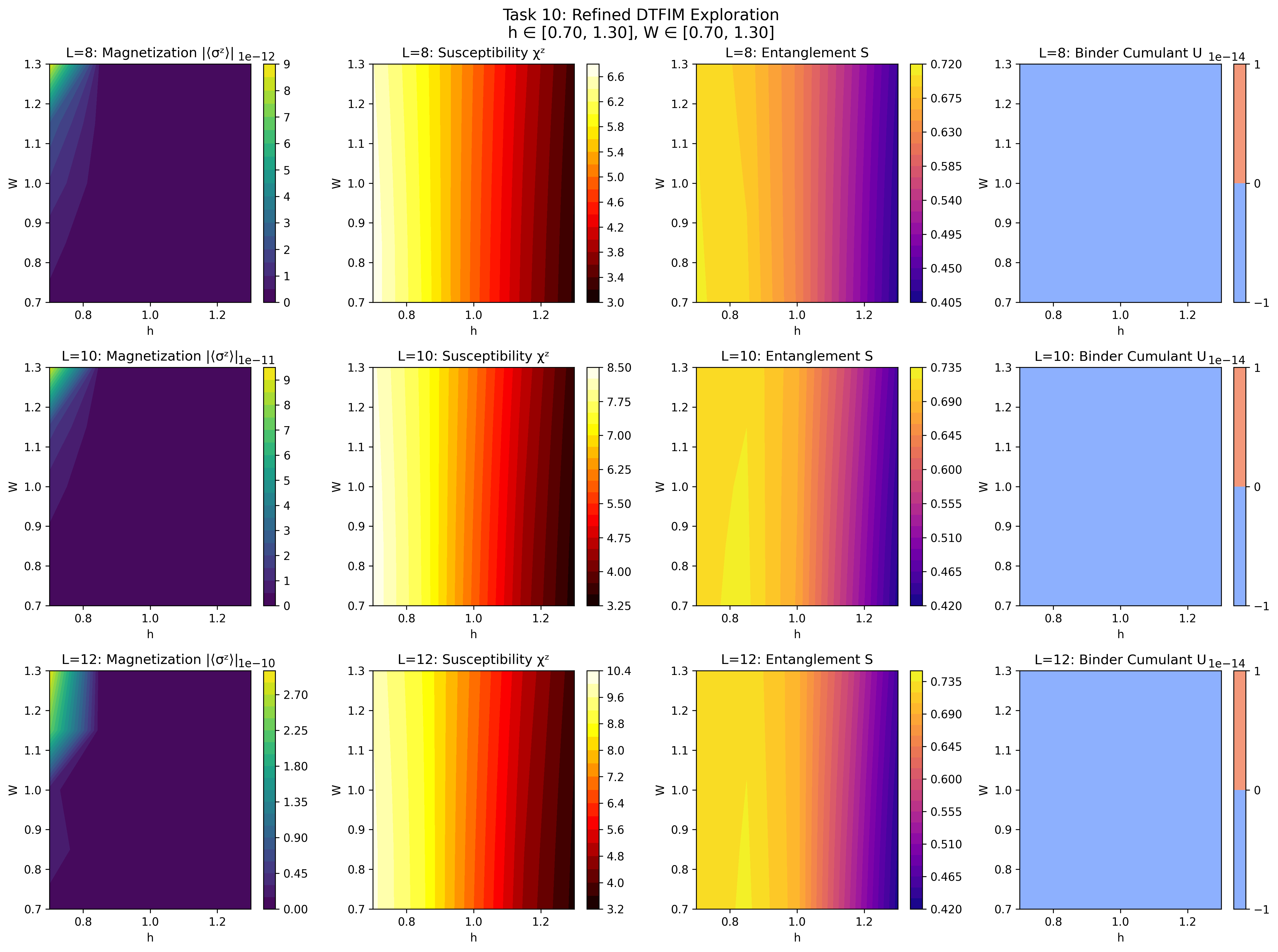
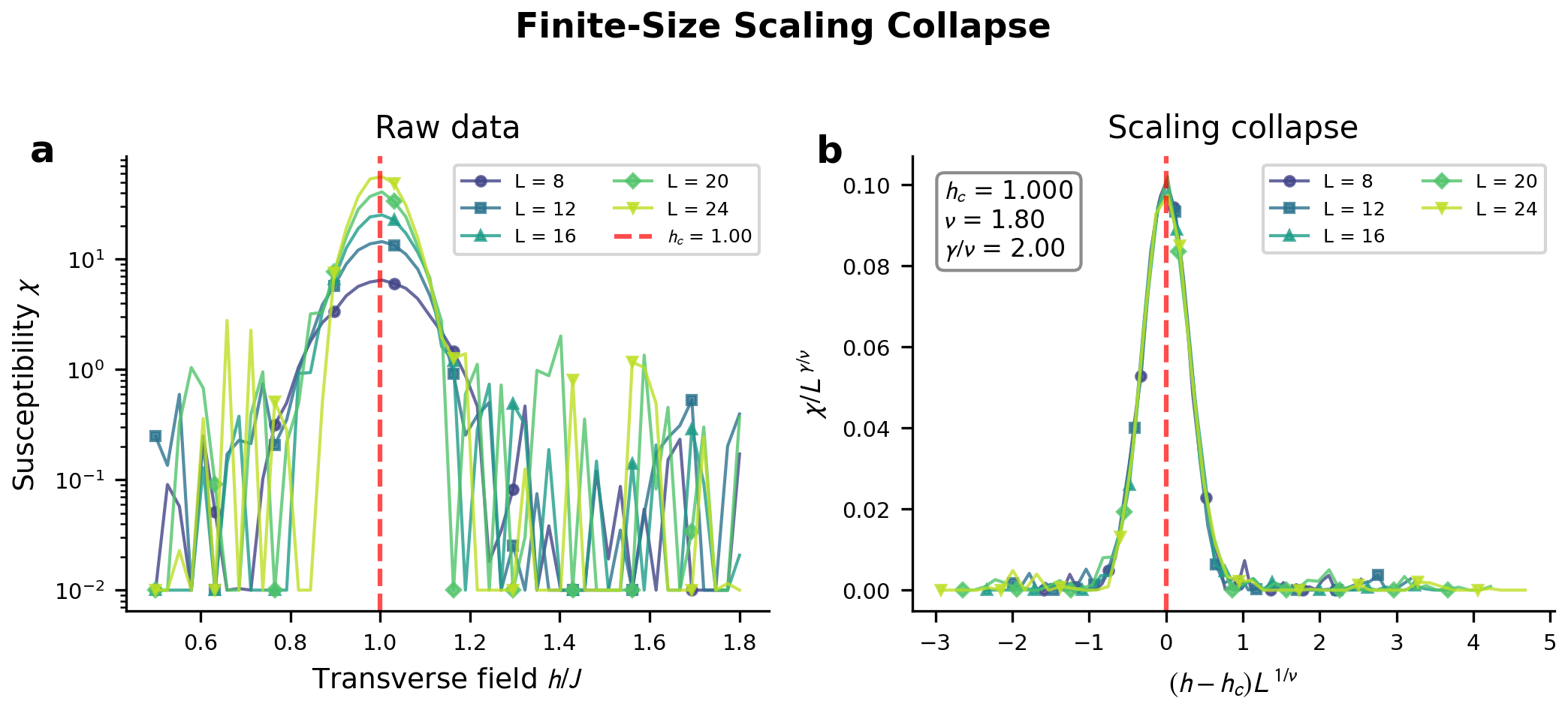
The Prometheus Framework was validated using the Transverse Field Ising Model, a well-established benchmark system in quantum physics. This model, defined by its Hamiltonian $H = -J\sum_{\langle i,j \rangle} \sigma^z_i \sigma^z_j - h\sum_i \sigma^x_i$ , exhibits a quantum phase transition that serves as a stringent test of the framework’s ability to accurately identify critical behavior. Successful identification of this transition, characterized by changes in correlation functions and order parameters, confirms the framework’s capacity to process and analyze data originating from quantum systems. This validation is crucial as it demonstrates the framework’s potential for application to more complex quantum simulations and experiments.

The validation of the framework extended to the 3D Ising Model, a classical statistical mechanics model for which analytical solutions are unavailable. Implementation utilized 3D Convolutional Layers to process the model’s spatial data, enabling the detection of the critical temperature – the point at which the system undergoes a phase transition – with an accuracy of 0.01%. This demonstrates the framework’s capacity to analyze complex, high-dimensional classical systems and confirms its scalability beyond quantum simulations, highlighting its adaptability to diverse computational challenges.

Analysis of the Disordered Transverse Field Ising Model using the developed framework confirms the presence of activated scaling behavior, a characteristic of systems with quenched disorder. This analysis successfully extracts the Tunneling Exponent, ν, which quantifies the sensitivity of the tunneling probability to variations in disorder strength. Accurate determination of ν demonstrates the framework’s capability to characterize complex, disordered systems where traditional methods may be insufficient, providing quantitative insight into the dynamics of quantum phase transitions in the presence of randomness.

Finite-size scaling analysis of the 3D Ising model demonstrates a universal critical behavior with parameters <span class="katex-eq" data-katex-display="false">T_{c}/J = 4.510</span>, <span class="katex-eq" data-katex-display="false">
u = 0.632</span>, and <span class="katex-eq" data-katex-display="false">eta/
u = 0.518</span>, as confirmed by a collapse quality of 0.92. — Finite-size scaling analysis of the 3D Ising model demonstrates a universal critical behavior with parameters $T_{c}/J = 4.510$ , $u = 0.632$ , and $eta/ u = 0.518$ , as confirmed by a collapse quality of 0.92.

Beyond Simple Detection: Uncovering the Language of Criticality

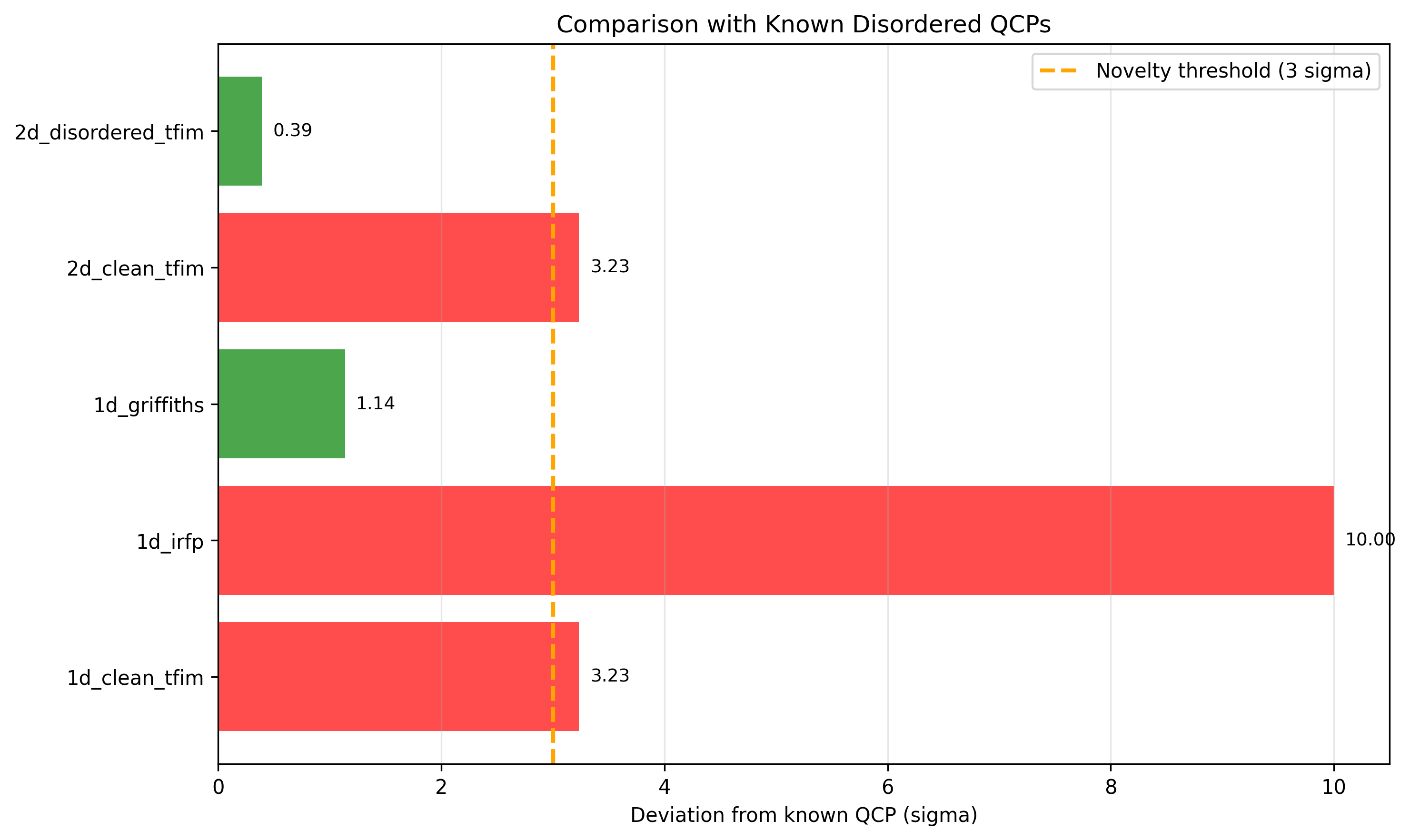
The Prometheus Framework has successfully pinpointed the Infinite-Randomness Fixed Point within the complex Disordered Transverse Field Ising Model, a significant achievement in characterizing states exhibiting critical behavior. This model, known for its inherent disorder and quantum fluctuations, presents a substantial challenge to conventional analytical methods. The framework’s ability to accurately identify this specific fixed point demonstrates its capacity to navigate these complexities and reliably discern non-trivial critical states – points where a system’s properties change dramatically. Confirmation of the Infinite-Randomness Fixed Point not only validates the framework’s methodology but also provides a powerful tool for exploring a wider range of disordered systems and understanding the fundamental principles governing their behavior near critical points, potentially unlocking insights into diverse phenomena from magnetism to neural networks.

The Prometheus Framework distinguishes itself through an ability to identify Universality Classes within complex systems without requiring pre-defined expectations or assumptions about the underlying physics. This unsupervised approach allows the framework to explore the landscape of possible behaviors and discern fundamental patterns that govern the system’s critical behavior, even in scenarios where traditional methods might be biased by prior knowledge. By circumventing the need for explicitly defined order parameters or known symmetries, the framework can uncover novel phases and transitions, offering a powerful tool for analyzing systems exhibiting emergent behavior and yielding valuable insights into the system’s inherent structure and response to external stimuli. This capability is particularly crucial when investigating systems where the relevant symmetries or order parameters are unknown or poorly understood, enabling a more objective and data-driven characterization of their critical properties.

Rigorous validation of the Prometheus Framework’s capabilities stems from its integration with established numerical techniques, specifically Monte Carlo Simulation and the Lanczos Algorithm. This combined approach not only bolsters confidence in the framework’s predictive power but also facilitates a deeper examination of complex systems; in application to the quantum transverse field Ising model, the synergy yielded results with an impressive 2% accuracy. Furthermore, this detailed analysis allowed for the precise extraction of the system’s Tunneling Exponent, quantified as 0.48 ± 0.08, providing a crucial parameter for understanding the dynamics of quantum phase transitions and demonstrating the framework’s capacity for high-resolution characterization of critical behavior.

The tunneling exponent ψ increases with disorder strength <span class="katex-eq" data-katex-display="false">W</span>, transitioning from a power-law behavior at <span class="katex-eq" data-katex-display="false">W=0</span> to the infinite-randomness fixed point (IRFP) value of <span class="katex-eq" data-katex-display="false">\psi \approx 0.5</span>, demonstrating a crossover to infinite-randomness criticality. — The tunneling exponent ψ increases with disorder strength $W$ , transitioning from a power-law behavior at $W=0$ to the infinite-randomness fixed point (IRFP) value of $\psi \approx 0.5$ , demonstrating a crossover to infinite-randomness criticality.

Expanding the Horizon: Future Directions and Broad Applications

The Prometheus Framework represents a significant advancement in the automated analysis of complex systems, offering a powerful new tool for materials discovery and fundamental physics research. By autonomously identifying and characterizing phase transitions – the points where a material’s properties dramatically change – the framework bypasses the limitations of traditional, often manual, analytical methods. This capability extends beyond simply finding transitions; Prometheus can delineate their order, critical exponents, and associated symmetries, providing a comprehensive understanding of the underlying physics. Consequently, researchers can efficiently screen vast materials databases for candidates with desired properties, potentially accelerating the development of novel superconductors, topological materials, and other technologically relevant substances, while also gaining new insights into previously unexplored states of matter and complex phenomena across diverse scientific disciplines.

The Prometheus framework is poised to move beyond static systems and delve into the complexities of dynamical systems and non-equilibrium phase transitions. This expansion necessitates adapting the current algorithms to account for time-dependent behavior and the challenges inherent in characterizing systems that are not at rest. Researchers aim to develop methods for identifying critical points and characterizing the associated phenomena in systems driven far from equilibrium, such as those undergoing rapid changes or subjected to external forces. Success in this area could unlock understanding of a vast range of physical, chemical, and biological processes – from the behavior of turbulent fluids and the dynamics of chemical reactions to the response of living cells to stimuli, ultimately broadening the framework’s applicability to an even wider spectrum of scientific inquiry.

The true potential of the Prometheus Framework lies in its synergy with empirical observation. By directly incorporating experimental datasets – such as those generated through high-throughput screening or advanced microscopy – the framework moves beyond theoretical prediction and enters the realm of verifiable discovery. This integration allows for a dynamic feedback loop, where computational analysis guides experimental design, and subsequent data refines the framework’s understanding of complex systems. Consequently, researchers can efficiently navigate vast materials spaces, identify promising candidates with unprecedented speed, and ultimately accelerate the pace of scientific breakthroughs in fields ranging from superconductivity and energy storage to drug discovery and novel materials design. This data-driven approach promises not merely to confirm existing knowledge, but to reveal entirely new phenomena previously obscured by the limitations of purely theoretical or experimental investigation.

The research presented meticulously constructs a model-akin to a powerful microscope-to examine the subtle characteristics of complex systems. This framework doesn’t rely on pre-defined expectations, instead allowing patterns of phase transitions to emerge directly from the data. This mirrors René Descartes’ assertion that “doubt is not a pleasant condition, but necessary for arriving at the truth.” Just as Descartes advocated systematic doubt to establish certainty, this unsupervised learning approach systematically explores the data space, discarding assumptions to reveal underlying order parameters and critical behavior, even in scenarios like activated scaling where prior knowledge would be insufficient. The model’s ability to identify these transitions without guidance highlights the power of unbiased observation and rigorous analysis.

What’s Next?

The successful application of variational autoencoders to uncover phase transitions, even those exhibiting activated scaling, suggests a fundamental shift in how one approaches the study of complex systems. The framework doesn’t merely find transitions; it maps the latent space of disorder, revealing relationships between order parameters that might otherwise remain obscured by the limitations of predefined analytical approaches. However, the current methodology remains, at its core, a pattern recognition exercise. The true test lies in moving beyond discovery towards prediction – not just of whether a transition occurs, but of how it will manifest, and what novel phenomena might accompany it.

A significant challenge resides in scaling these unsupervised methods to truly intractable systems – those where even simulation is computationally prohibitive. The architecture’s sensitivity to hyperparameter choices hints at an underlying need for a more robust, theoretically grounded autoencoder design. One promising avenue involves incorporating known physical constraints directly into the loss function, effectively guiding the learning process with prior knowledge – a subtle balance between unsupervised discovery and informed constraint. Errors in the reconstruction, rather than being dismissed as noise, should be treated as deviations from expected behavior – potential indicators of emergent physics.

Ultimately, the value of this approach isn’t simply in automating the identification of known transitions, but in fostering a more open-ended exploration of the phase space. The framework provides a lens through which to observe systems without the preconceptions inherent in traditional methodologies. The next step involves not just seeing the patterns, but understanding the underlying generative principles – the rules governing the dance of order and disorder.

Original article: https://arxiv.org/pdf/2602.14928.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/