Uncovering Hidden Patterns in Quantum Quenches

Author: Denis Avetisyan

New research reveals how spatial variations dramatically influence the behavior of interacting electrons after a sudden change in their environment.

Following a sudden shift in interaction strength, the system’s double occupancy - a measure of paired particles - exhibits time-dependent fluctuations whose period and long-term average are demonstrably modulated by the magnitude of that shift, revealing a nuanced relationship between quench strength <span class="katex-eq" data-katex-display="false">U_f/W</span> and the resulting dynamic behavior. — Following a sudden shift in interaction strength, the system’s double occupancy – a measure of paired particles – exhibits time-dependent fluctuations whose period and long-term average are demonstrably modulated by the magnitude of that shift, revealing a nuanced relationship between quench strength $U_f/W$ and the resulting dynamic behavior.

This study demonstrates the critical role of spatial inhomogeneities in the nonequilibrium dynamics of strongly correlated electron systems, extending beyond traditional spatially uniform approximations like DMFT.

While spatially homogeneous theories dominate the study of far-from-equilibrium quantum systems, they may overlook crucial emergent behavior in strongly correlated materials. This is addressed in ‘Emergent Spatial Textures from Interaction Quenches in the Hubbard Model’, which investigates the dynamics following a sudden change in interactions within the Hubbard model using a real-space time-dependent Gutzwiller approach. Our findings reveal that even weak spatial fluctuations grow dynamically, driving the system towards intrinsically inhomogeneous states characterized by the nucleation and coarsening of Mott-like domains. Do these results suggest that spatial self-organization is a generic feature of driven correlated matter, fundamentally limiting the validity of spatially uniform theoretical descriptions?

Beyond Equilibrium: The Emergence of Nullquilibrium Dynamics

For decades, condensed matter physics largely operated under the assumption of equilibrium – a state where properties remain constant over time. This framework, while successful in describing many materials, inherently restricts the exploration of systems constantly subjected to external forces or ‘driven’ systems. The equilibrium approach struggles to account for the rich and often unpredictable behaviors arising from these non-equilibrium conditions. Consider a material absorbing light, or a battery discharging – these are inherently dynamic processes where the system is never truly at rest. By primarily focusing on equilibrium states, a significant portion of the physical world, and the novel phenomena within it, remained largely unexplored. This limitation motivates a shift towards understanding systems far from equilibrium, opening avenues for discovering entirely new states of matter and unlocking a deeper comprehension of fundamental physical processes.

The exploration of systems operating far from thermodynamic equilibrium, a field termed ‘nullquilibrium Dynamics’, represents a critical frontier in modern physics. Traditional condensed matter studies frequently rely on the assumption of equilibrium, which significantly restricts the investigation of processes driven by external forces or internal interactions. However, many real-world phenomena, from the behavior of biological systems to the emergence of novel materials, occur in decidedly non-equilibrium conditions. By focusing on these transient, dynamic states, researchers aim to uncover fundamental physical processes and potentially discover entirely new states of matter not accessible under equilibrium constraints. This approach offers a pathway to understanding complex systems where energy is constantly flowing and structures are perpetually evolving, ultimately expanding the scope of materials science and fundamental physics beyond the limitations of static, balanced states.

The intricacies of interacting quantum systems, often modeled by the $Hubbard Model$ , become particularly accessible when examined through the lens of `nullquilibrium Dynamics`. This approach moves beyond static equilibrium states to explore how these systems evolve under external drives or perturbations. The $Hubbard Model$ , which describes electrons interacting on a lattice, exhibits a rich phase diagram – from insulating to metallic states – and understanding the dynamics of transitions between these states, or the response to pulsed drives, necessitates a `nullquilibrium` perspective. Traditional methods, focused on ground states, often fail to capture the transient, non-equilibrium behaviors that govern phenomena like high-temperature superconductivity or the creation of exotic quantum phases. By focusing on the time evolution of quantum correlations and excitations, `nullquilibrium Dynamics` offers a powerful framework for unraveling the complex behavior of these fundamentally interacting systems and predicting their responses to external stimuli.

Understanding the fleeting behaviors of $nullquilibrium$ dynamics necessitates techniques capable of resolving events on incredibly short timescales. Ultrafast spectroscopy emerges as a pivotal tool, employing laser pulses lasting mere femtoseconds – quadrillionths of a second – to initiate and then monitor the system’s response. This approach doesn’t observe a static, equilibrium state, but rather captures the transient evolution of the system as it moves through a series of non-equilibrium configurations. By analyzing changes in the material’s optical properties following excitation, researchers can map the pathways of energy and charge flow, unveiling the mechanisms governing these complex, driven systems. This allows for direct observation of correlated electron behavior and the emergence of novel quantum phases, providing insights unattainable through traditional, static measurements.

The site-averaged spectral weight <span class="katex-eq" data-katex-display="false">\mathcal{Z}(t)</span> exhibits distinct dynamics depending on quench strength, transitioning from sustained oscillations for weak quenches to damped behavior for stronger ones, as summarized by the averaged spectral weight <span class="katex-eq" data-katex-display="false">\langle\mathcal{Z}\rangle</span> as a function of final to initial strength ratio <span class="katex-eq" data-katex-display="false">U_f/W</span>. — The site-averaged spectral weight $\mathcal{Z}(t)$ exhibits distinct dynamics depending on quench strength, transitioning from sustained oscillations for weak quenches to damped behavior for stronger ones, as summarized by the averaged spectral weight $\langle\mathcal{Z}\rangle$ as a function of final to initial strength ratio $U_f/W$ .

Driving Systems Out of Balance: Quantum Quenches

A quantum quench is defined by the instantaneous modification of a system parameter – such as magnetic field, interaction strength, or lattice potential – that governs the Hamiltonian of a quantum many-body system. This abrupt change initiates a non-equilibrium dynamic as the system evolves from its initial, typically ground state, to a new state dictated by the altered Hamiltonian. Importantly, the timescale of this parameter change is assumed to be much shorter than any characteristic timescale associated with the system’s dynamics, ensuring that the initial state remains unperturbed during the quench itself. This process fundamentally differs from adiabatic parameter changes and results in excitations across the energy spectrum, leading to complex correlations and observable consequences in the system’s subsequent evolution.

Following a quantum quench, the abrupt alteration of a system parameter initiates non-equilibrium dynamics characterized by the time-dependent evolution of correlations. Initially, localized disturbances propagate and interact, leading to the creation of entangled states and complex many-body correlations. The nature of these correlations-whether short-ranged or long-ranged-and their subsequent evolution are determined by the specific quench protocol and the system’s underlying interactions. Analyzing the time-dependence of correlation functions, such as $\langle O(t) O(0) \rangle$ , provides insight into the relaxation processes and the emergence of new steady states, potentially revealing exotic phases of matter inaccessible in equilibrium.

The Single-Band Hubbard Model, a cornerstone of condensed matter physics, offers a computationally feasible yet physically relevant system for investigating the dynamics following a quantum quench. This model, describing interacting fermions on a lattice, simplifies many-body interactions while retaining essential physics. Importantly, the model’s parameters can be experimentally controlled via Feshbach tuning in ultracold atomic gases. Feshbach tuning manipulates the scattering length, effectively controlling the strength of interactions $U$ between particles within the Hubbard Hamiltonian $H = -t \sum_{\langle i,j \rangle} (c^{\dagger}_i c_j + h.c.) + U \sum_i n_i(n_i - 1)$ , where $t$ represents the hopping parameter and $n_i$ is the particle number operator at site $i$ . This tunability allows researchers to explore a wide range of interaction strengths and study the resulting non-equilibrium dynamics with direct experimental relevance.

Modeling the dynamics following a quantum quench requires theoretical tools specifically designed to address strong interactions and spatial inhomogeneities, as perturbative methods often fail in these regimes. Approaches such as Dynamical Mean-Field Theory (DMFT) and its extensions, like spatially-resolved DMFT, can effectively capture local correlations arising from strong interactions. Furthermore, techniques like Quantum Monte Carlo (QMC), while computationally demanding, provide benchmark results for verifying other theoretical methods. For spatially inhomogeneous systems, Density Functional Theory (DFT) and Time-Dependent DFT (TDDFT) offer viable pathways, though accurately representing strong correlations within these frameworks remains a challenge. The choice of method depends on the specific system and the desired level of accuracy, with ongoing research focused on developing more efficient and reliable techniques for tackling these complex many-body problems.

Following a quench to <span class="katex-eq" data-katex-display="false">U_f/W = 0.72</span>, the system exhibits coarsening dynamics characterized by domain nucleation and growth, as evidenced by the time evolution of the average double occupancy <span class="katex-eq" data-katex-display="false">\mathcal{D}(t)</span>, its spatial standard deviation <span class="katex-eq" data-katex-display="false">\sigma_{\mathcal{D}}(t)</span>, and density fluctuations <span class="katex-eq" data-katex-display="false">\sigma_n(t)</span>, alongside snapshots and distributions of the local double occupancy <span class="katex-eq" data-katex-display="false">\mathcal{D}_i</span>. — Following a quench to $U_f/W = 0.72$ , the system exhibits coarsening dynamics characterized by domain nucleation and growth, as evidenced by the time evolution of the average double occupancy $\mathcal{D}(t)$ , its spatial standard deviation $\sigma_{\mathcal{D}}(t)$ , and density fluctuations $\sigma_n(t)$ , alongside snapshots and distributions of the local double occupancy $\mathcal{D}_i$ .

Revealing Spatial Inhomogeneities: Real-Space Dynamics

The Real-Space Time-Dependent Gutzwiller Approximation (TDGA) is a computational method used to model the dynamic behavior of strongly correlated quantum many-body systems while retaining spatial information. Unlike mean-field approaches that average over spatial degrees of freedom, TDGA solves for the local wavefunction at each lattice site, enabling the observation of spatially varying quantities and the evolution of patterns. This is achieved by approximating the many-body wavefunction as a product of single-site wavefunctions and employing a time-dependent variational principle based on the $\text{Von Neumann equation}$ . The method is particularly suited for studying non-equilibrium dynamics, such as those induced by quenches, and for investigating the emergence of spatially inhomogeneous phases like those found in Mott insulators, where electron correlations lead to localized behavior and spatial variations in density and order parameters.

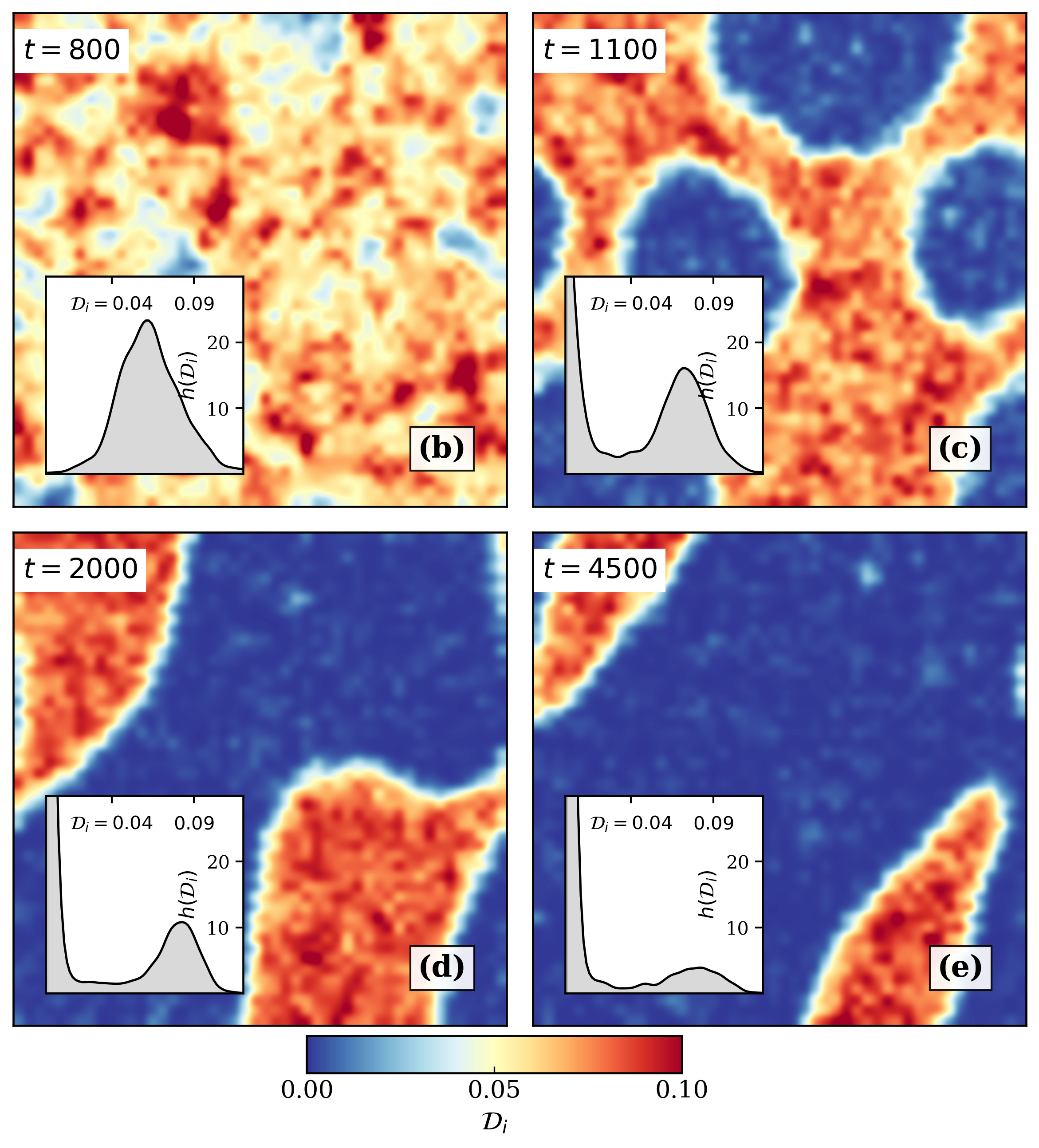
The Real-Space Time-Dependent Gutzwiller Approximation (TDGA) facilitates the observation of Spatial Inhomogeneities by extending the standard Gutzwiller Approximation to incorporate spatial coordinates and time evolution. This allows for the direct mapping of density and coherence variations across a system as it dynamically evolves, revealing how localized regions with differing physical properties emerge and interact. By tracking these inhomogeneities, the TDGA enables the investigation of their impact on macroscopic system behavior, such as transport properties and collective excitations, offering insights beyond those obtainable from spatially averaged approaches. The method achieves this by solving a time-dependent set of equations for local density matrices, effectively simulating the dynamics of the many-body wavefunction while retaining spatial resolution.

The Gutzwiller von Neumann Dynamics represent a computational approach to simulating strongly correlated systems by integrating the Von Neumann equation within the Time-Dependent Gutzwiller Approximation (TDGA). This method propagates the system’s wavefunction in time by solving the $i\hbar \frac{\partial}{\partial t} |\psi(t)\rangle = H|\psi(t)\rangle$ equation, but does so within the mean-field framework of the Gutzwiller Approximation, which decouples fluctuations and simplifies the many-body problem. The resulting dynamics are computationally tractable while retaining a description of spatial inhomogeneities, and are particularly effective in modeling the non-equilibrium behavior of interacting quantum systems, offering a robust framework for analyzing phenomena such as the formation and evolution of Mott-like regions.

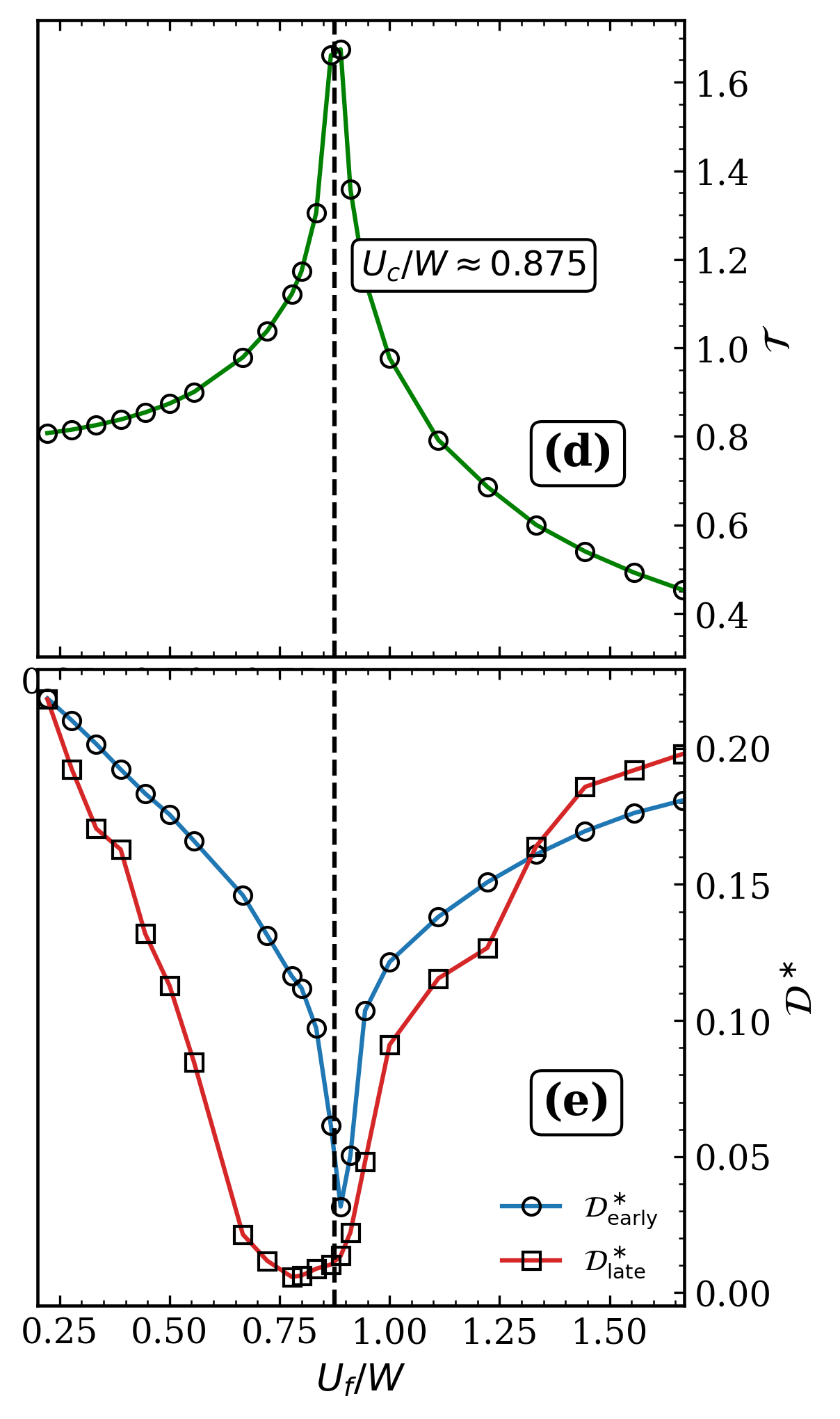
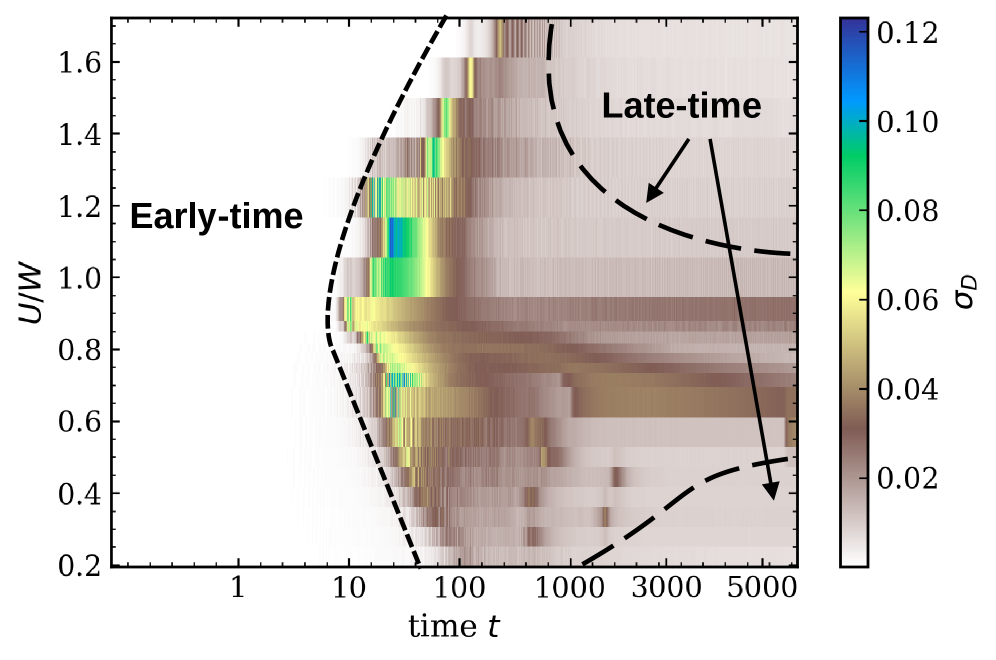
Simulations utilizing the Real-Space Time-Dependent Gutzwiller Approximation demonstrate the formation of spatially localized, insulating Mott-like regions following a system quench. These regions are characterized by reduced kinetic energy and suppressed single-particle coherence, resulting in Spatial Dephasing of the wavefunction. Analysis reveals that these insulating domains initially nucleate at defects or regions of high interaction strength, then undergo a slow coarsening process where larger, more stable regions grow at the expense of smaller ones. This nucleation and coarsening behavior is a key observation, indicating a dynamic evolution towards a spatially inhomogeneous ground state and provides insight into the non-equilibrium dynamics of strongly correlated systems.

The spatial fluctuation of double occupancy <span class="katex-eq" data-katex-display="false">\sigma_{\mathcal{D}}(t)</span> transitions from homogeneous behavior at early times to inhomogeneous behavior at intermediate times as interaction strength <span class="katex-eq" data-katex-display="false">U_f/W</span> changes, as indicated by the dashed boundaries. — The spatial fluctuation of double occupancy $\sigma_{\mathcal{D}}(t)$ transitions from homogeneous behavior at early times to inhomogeneous behavior at intermediate times as interaction strength $U_f/W$ changes, as indicated by the dashed boundaries.

Refining the Model: Lattice Effects and Disorder

The fundamental arrangement of atoms within a material, specifically the geometry of its underlying lattice, profoundly influences how a system responds to a sudden change-a ‘quench’-in its parameters. Consider a $Triangular Lattice$ ; its unique connectivity dictates the pathways available for excitations to propagate and interact following the quench. Unlike systems with simpler lattice structures, the triangular arrangement introduces anisotropic effects, meaning the dynamics differ depending on the direction. This geometric constraint alters the energy landscape, creating localized states and influencing the overall rate of thermalization. Consequently, the time evolution of observables, such as the double occupancy or spectral weight, deviates significantly from predictions based on homogeneous, translationally invariant models. Understanding these lattice effects is crucial for accurately modeling and predicting the behavior of complex quantum systems subjected to rapid changes.

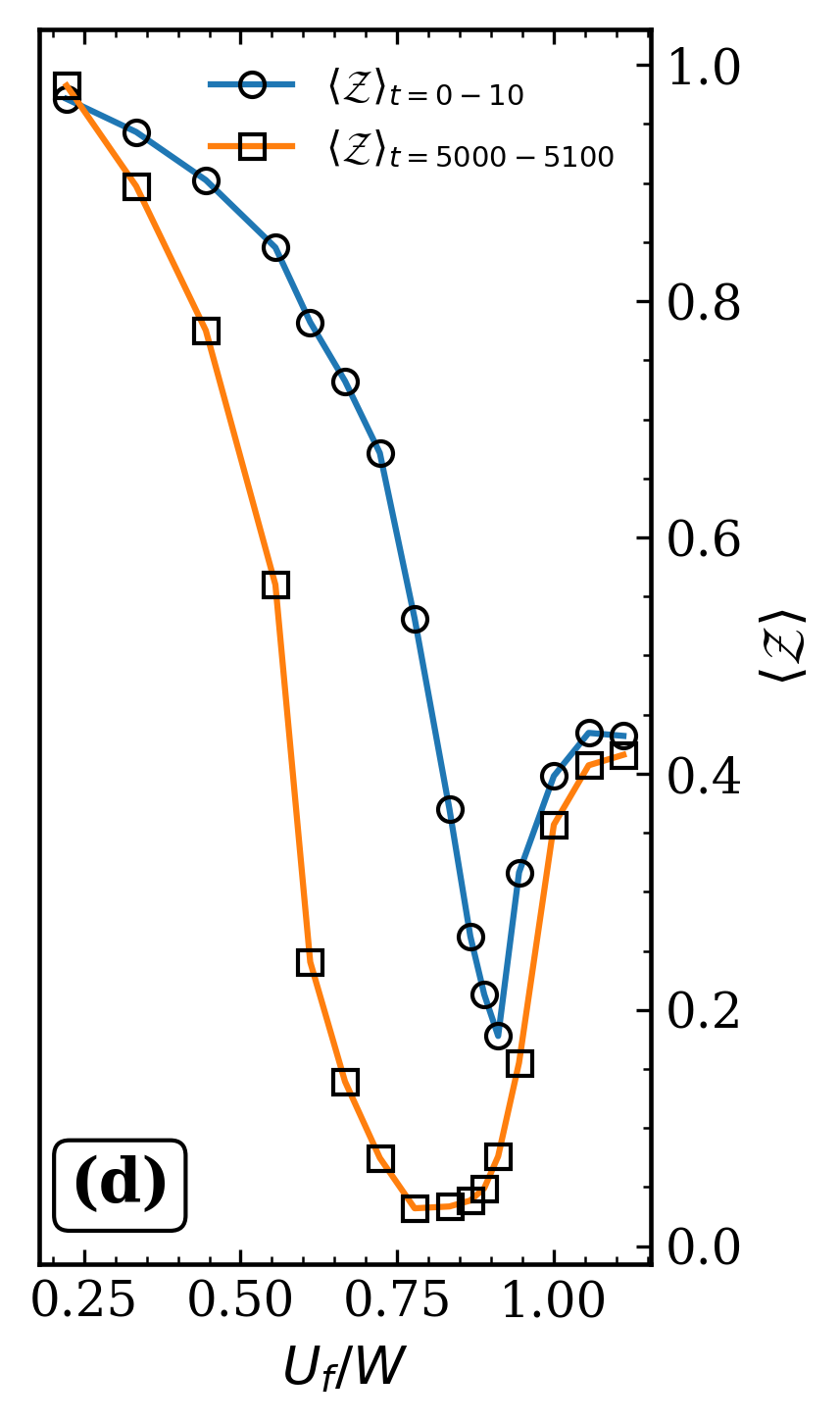
The introduction of $Anderson$ disorder, a subtle, localized energy variation at each lattice site, fundamentally alters the system’s dynamic evolution. This weak, on-site potential doesn’t simply add noise; it actively seeds spatial fluctuations in the quantum state. Instead of a uniform response to the quench, the disorder creates localized regions where the system evolves differently, leading to a more complex and fragmented dynamic. These fluctuations inhibit the propagation of coherence, preventing the establishment of long-range order and creating a textured, rather than monolithic, response to the sudden change in parameters. Consequently, the system’s behavior diverges from predictions based on perfectly homogeneous conditions, revealing the profound impact even seemingly minor imperfections can have on quantum dynamics.

The intricate interplay between the underlying lattice structure and the introduction of disorder profoundly impacts the system’s spectral weight and, consequently, its quantum coherence. Deviations in the time-evolved spectral weight, denoted as $𝒵(t)$ , from predictions made by homogeneous Time-Dependent Gutzwiller Ansatz (TDGA) reveal this influence. These discrepancies aren’t merely quantitative; they indicate a reshaping of the energy distribution within the system due to the lattice geometry and the presence of disorder. Specifically, the lattice constrains particle movement, while disorder introduces localized fluctuations, both contributing to a more complex spectral landscape than anticipated by simpler, homogeneous models. This alteration in the spectral weight directly reflects a diminished ability of the system to maintain quantum coherence over time, as the energy distribution broadens and delocalization is hindered, highlighting the crucial role of these structural elements in controlling quantum dynamics.

Investigations into the system’s relaxation behavior reveal a distinct correlation between system size and the rate of equilibration. Specifically, simulations demonstrate that for systems containing fewer than 30 lattice sites $(L < 30)$ , the double occupancy $𝒟(t)$ – a measure of multiple occupancy on each lattice site – relaxes much more quickly towards its equilibrium value. However, as the system expands to include 30 or more lattice sites $(L \geq 30)$ , the time-dependent changes in the double occupancy become significantly subdued, indicating a weakening of finite-size effects. This suggests that larger systems are approaching the behavior of an infinite lattice, providing a more accurate representation of the underlying physics and reducing the influence of boundary conditions on the observed dynamics.

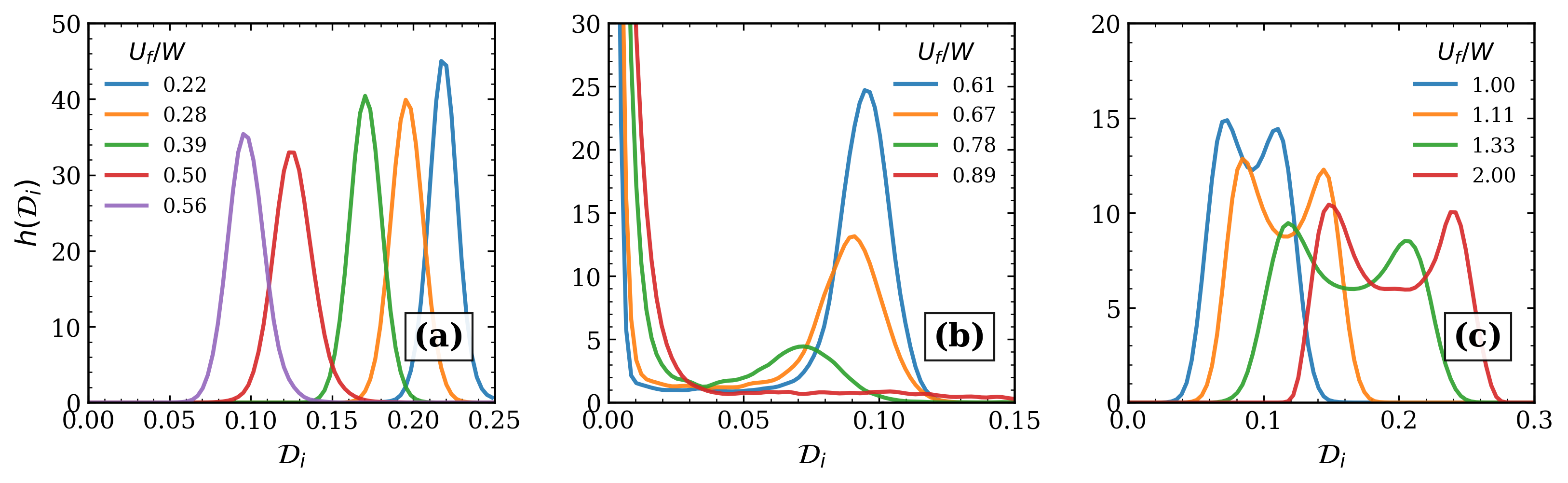
Analysis of local double occupancy <span class="katex-eq" data-katex-display="false">\mathcal{D}_{i}(t)</span> across a 48x48 lattice reveals distinct probability distributions depending on the strength of the quench, ranging from weak to strong coupling. — Analysis of local double occupancy $\mathcal{D}_{i}(t)$ across a 48×48 lattice reveals distinct probability distributions depending on the strength of the quench, ranging from weak to strong coupling.

The research elucidates how complex spatial textures emerge organically from local interactions within the Hubbard model, a phenomenon resonating with David Hume’s observation: “The mind receives simple impressions from simple objects, and then combines them to form complex ideas.” The study demonstrates that these ‘complex ideas,’ or spatial inhomogeneities, aren’t imposed but arise spontaneously from the system’s response to a quantum quench. This echoes the principle that order doesn’t require architects; instead, it emerges from the interplay of local rules governing electron behavior. The time-dependent Gutzwiller approximation used here doesn’t dictate the resulting patterns; it allows them to self-organize, reinforcing the notion that self-organization consistently proves stronger than forced design.

The Forest Keeps Growing

The tendency to seek a guiding hand, a central control, is persistent even when observation reveals its absence. This work, by focusing on the intrinsic development of spatial structure following a disturbance, subtly reinforces that principle. The Hubbard model, a deceptively simple framework, demonstrates that complex patterns aren’t necessarily designed; they arise from local interactions. The forest evolves without a forester, yet follows rules of light and water. The remaining challenge isn’t to impose order, but to better understand the rules governing this self-organization-to map the landscape of possible emergent textures.

Current theoretical approaches, often rooted in spatial homogeneity, appear increasingly as simplifications – useful sketches, perhaps, but far from the territory itself. The true dynamics likely reside in the interplay between these local rules and long-range correlations, a coupling that requires methodologies beyond current dynamical mean-field theory approximations. Exploring the robustness of these textures to imperfections-to the inevitable ‘gaps in the canopy’-represents a crucial next step.

Ultimately, this line of inquiry suggests a shift in perspective. Rather than asking how to control strongly correlated systems, the more fruitful question may be: how can one influence the conditions under which desired patterns are more likely to emerge? Order is the result of local interactions, not directives. The details, as always, will be found not in the blueprint, but in the growth itself.

Original article: https://arxiv.org/pdf/2601.22053.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Beyond Equilibrium: The Emergence of Nullquilibrium Dynamics

Driving Systems Out of Balance: Quantum Quenches

Revealing Spatial Inhomogeneities: Real-Space Dynamics

Refining the Model: Lattice Effects and Disorder

The Forest Keeps Growing

See also: