Author: Denis Avetisyan
Researchers have refined a powerful computational technique to accurately model the behavior of unstable nuclei, paving the way for a deeper understanding of nuclear structure.
This work presents improvements to the Gamow Density Matrix Renormalization Group (G-DMRG) method for calculating broad resonances in light nuclei using optimized reference spaces and truncation schemes.
Predicting the properties of exotic nuclei, particularly those near the drip lines, remains a central challenge in nuclear physics due to uncertainties in nuclear forces and the complexities of describing open quantum systems. This work presents advancements in the \textit{ab initio} Gamow Density Matrix Renormalization Group (G-DMRG) method, detailed in ‘Ab initio Gamow density matrix renormalization group for broad nuclear many-body resonances’, to address these limitations by enabling accurate calculations of broad many-body resonances. Through optimized reference space construction, entanglement-driven orbital ordering, and novel truncation schemes, we demonstrate control over calculations in extreme conditions and achieve convergence patterns in light nuclei like ^{5,6}\text{He} and ^{4}\text{H}. Will these techniques pave the way for systematic studies of nuclear forces and a more complete understanding of the nuclear landscape?
The Inevitable Complexity of Fleeting States
The description of resonant states, particularly those exhibiting substantial decay widths – often termed ‘BroadManyBodyResonances’ – presents a significant challenge to conventional theoretical approaches in nuclear physics. These resonances, representing temporary, quasi-bound states within a system, are fundamental to understanding how nuclei interact and transform during scattering events and reactions. Traditional methods, relying on approximations that assume well-defined energy levels and negligible decay, frequently fail to accurately capture the behavior of these broad resonances. This limitation hinders precise predictions of reaction rates and cross-sections, as well as a complete understanding of nuclear structure itself. The difficulty arises because broad resonances are not easily characterized by a single energy value; instead, they exist as a distribution of energies, demanding a more sophisticated theoretical treatment that can effectively account for the inherent uncertainty and rapid decay of these fleeting states.
Resonances serve as pivotal intermediaries in scattering processes and energy transfer within complex systems, dictating reaction rates and pathways; however, their inherently short lifetimes and broad energy profiles present a significant theoretical challenge. Traditional frameworks, built upon the assumption of stable, well-defined energy states, struggle to accurately capture the fleeting existence and complex decay mechanisms of these resonances. Consequently, a departure from standard Hermitian quantum mechanics is becoming increasingly necessary, demanding innovative approaches like the complex scaling method or the inclusion of explicitly non-Hermitian Hamiltonians. These new theoretical tools aim to directly address the resonances’ complex energies – represented as E = E_R - \frac{i\Gamma}{2}, where Γ denotes the decay width – allowing for a more realistic and predictive understanding of nuclear reactions, molecular dynamics, and other phenomena governed by transient states.
The conventional framework of Hermitian quantum mechanics, while remarkably successful in describing stable systems, proves inadequate when addressing the inherently transient nature of resonant states. These states, representing temporary configurations before decay, demand a theoretical approach that explicitly accounts for energy loss and the probabilistic character of their disappearance. Describing decay dynamics accurately requires moving beyond the confines of a static Hamiltonian and embracing formalisms-such as the complex scaling method or the use of complex absorbing potentials-that allow for the incorporation of complex energies and the natural representation of outgoing waves. This shift acknowledges that resonances are not simply solutions to the time-independent Schrödinger equation, but rather poles in a complex energy plane, where the imaginary part of the energy directly relates to the decay rate Γ. Consequently, a complete understanding of resonant phenomena in complex systems hinges on abandoning the strict adherence to Hermitian operators and adopting a more nuanced, non-Hermitian quantum mechanical description.
Extending the Toolkit: A Complex-Energy Solution
Gamow Density Matrix Renormalization Group – G-DMRG – builds upon the numerical efficiency of Density Matrix Renormalization Group – DMRG – by extending its capabilities to complex energy domains. Traditional DMRG is limited to real energies, hindering the accurate representation of short-lived resonant states which exhibit finite lifetimes. G-DMRG addresses this limitation by allowing calculations with complex-valued energies, effectively treating resonances as quasi-stationary states with a finite decay rate. This approach enables the determination of both the energy and lifetime of resonant states, providing a complete description of their dynamic behavior within a many-body quantum system. The method retains DMRG’s ability to efficiently handle strongly correlated systems while incorporating the physics necessary to describe states that decay over time.
Gamow-DMRG utilizes \text{ComplexEnergyGamowStates} which are wavefunctions defined for complex energies, enabling the direct calculation of resonance lifetimes and decay rates. These states are expanded in a \text{BerggrenBasis}, a carefully constructed set of functions including both bound and unbound states, which is crucial for accurately representing the continuum spectrum relevant to resonance decay. Traditional methods often struggle with resonances due to their inherently unstable nature and the difficulties in representing the continuum, but the combination of complex energy states and the Berggren basis in Gamow-DMRG provides a robust framework for modeling these decaying states and extracting their key properties, such as energy and width.
The Quasi-Stationary Formalism (QSF) simplifies the many-body problem by focusing on the relevant subspace of states that contribute significantly to the resonance, rather than attempting to diagonalize the full Hamiltonian. This approach leverages the observation that resonant states, while not true eigenstates, have a finite lifetime and thus occupy a limited Hilbert space. By projecting the Hamiltonian onto this subspace, G-DMRG effectively reduces the dimensionality of the problem, enabling efficient calculations of resonant energies and wavefunctions. The QSF achieves this by defining a non-Hermitian effective Hamiltonian H_{eff} = H - i\frac{W}{2}, where W represents a complex energy broadening parameter, allowing for the treatment of decaying states as quasi-stationary states with finite lifetimes. This simplification is crucial for extending DMRG to handle resonances, which are inherently unstable and require a different mathematical treatment than traditional bound states.
Fine-Tuning the Machine: Accuracy and Efficiency
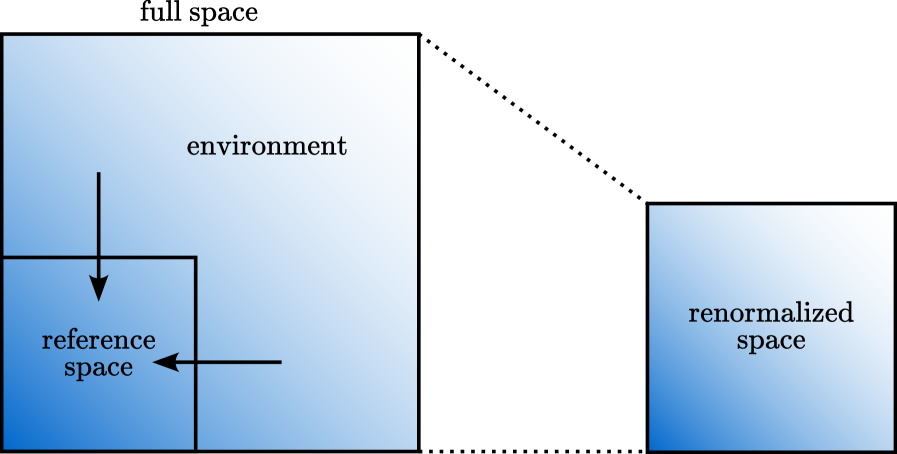
Effective application of the Group-DMRG (G-DMRG) method for many-body problems necessitates a carefully designed `ReferenceSpaceConstruction`. This process involves selecting a subset of single-particle states – the reference space – that effectively captures the dominant correlations within the system. A well-chosen reference space minimizes the size of the Hilbert space requiring explicit diagonalization, thereby reducing computational cost and accelerating convergence. The construction often prioritizes states near the Fermi level or those with significant overlap with the ground state wave function, ensuring that essential physics is retained while discarding less relevant configurations. The accuracy of G-DMRG calculations is directly linked to the quality of this initial reference space selection; an inadequate choice can lead to inaccurate results or require significantly larger basis sets to achieve convergence.
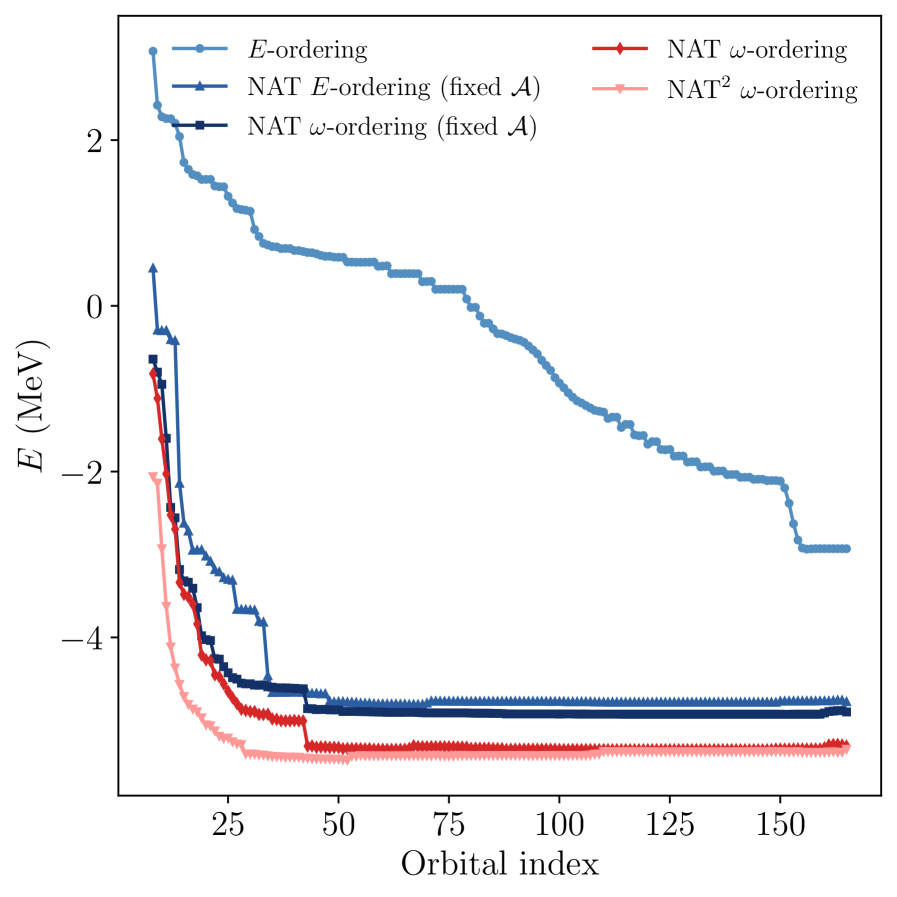
Employing a NaturalOrbitalBasis within G-DMRG calculations optimizes the representation of the many-body wave function, leading to both faster convergence and reduced computational expense. This approach transforms the initial, often arbitrary, basis into a set of orbitals ordered by their occupation numbers, effectively concentrating the variational space on the most important configurations. By truncating the basis at a significantly lower dimension while retaining essential physics, the computational cost associated with storing and manipulating the density matrix is substantially decreased. This is particularly advantageous for larger systems or those requiring high-precision calculations, as it allows for the efficient exploration of the Hilbert space and reduces the number of retained states needed to achieve a target level of accuracy.
Wilsonian renormalization, a core principle of Density Matrix Renormalization Group (DMRG) and its generalization, G-DMRG, operates by iteratively eliminating degrees of freedom associated with high-energy excitations. This process effectively reduces the Hilbert space dimension while preserving the low-energy physics of the system. By systematically decoupling high-energy states, the computational cost scales polynomially with system size, rather than exponentially, as would be required for a direct diagonalization approach. This allows for the treatment of larger systems and more accurate calculations of ground-state properties and low-lying excitations, even for strongly correlated quantum many-body problems. The retained degrees of freedom represent the essential physics at a given energy scale, while the discarded states contribute negligibly to the low-energy behavior.
The accurate representation of many-body wavefunctions within the G-DMRG framework necessitates the use of \text{ComplexSymmetricDensityMatrices}. This is because the Hamiltonian, and consequently the energies and eigenstates, can be complex-valued, particularly when dealing with resonances or non-Hermitian effective Hamiltonians. Standard density matrix representations require complex conjugation for Hermitian Hamiltonians; however, G-DMRG directly operates on complex density matrices without this restriction, allowing for the efficient description of states with complex energies and facilitating calculations of resonance properties and scattering amplitudes. The complex symmetry ensures proper normalization and physical interpretation of the wavefunction despite the complex nature of the involved energies.
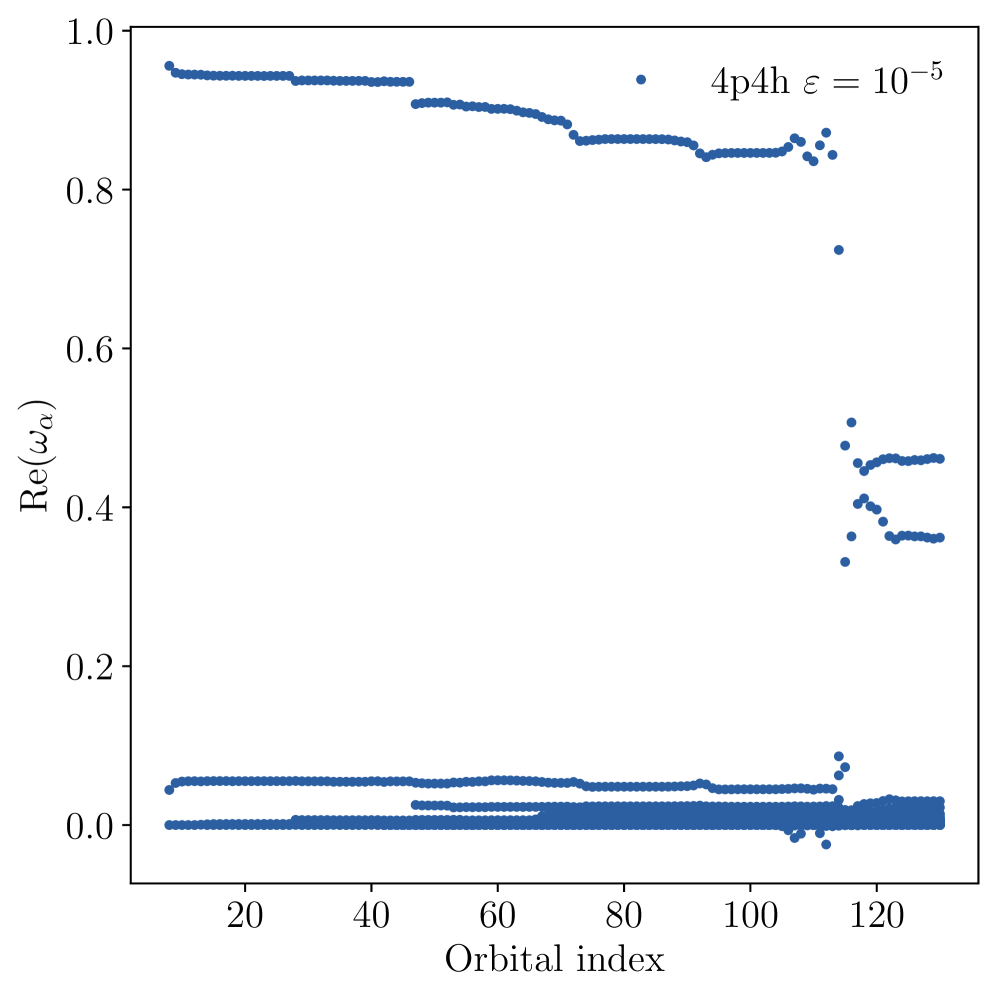
Ab initio G-DMRG calculations have been successfully applied to the description of broad many-body resonances present in light nuclei. Specifically, convergence has been demonstrated in calculations performed on Helium-4 (He^4), Hydrogen-4 (H^4), and Hydrogen-5 (H^5). This represents an expansion of the method’s applicability to systems exhibiting significant multi-particle correlations and extending beyond ground-state properties to encompass resonant states. The demonstrated convergence validates the framework’s ability to accurately represent the complex wavefunctions associated with these resonances, providing a benchmark for future calculations on more complex nuclear systems.
Confirming the Model: Validation and Wider Impact
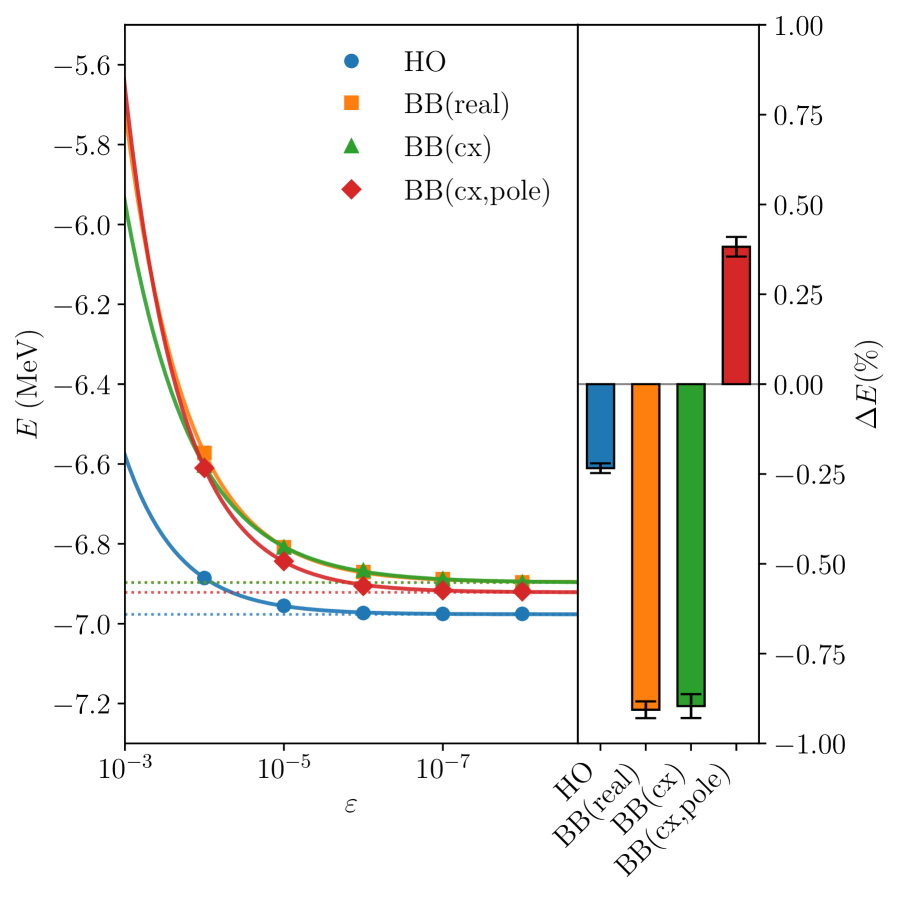
Rigorous validation of the Generalized Density Matrix Renormalization Group – G-DMRG – methodology has been achieved through direct comparison with the established No-Core Shell Model – NCGSM – framework. This independent assessment, conducted on Helium-3, reveals a remarkable level of agreement, with deviations consistently remaining below 1% relative to NCGSM results. Such close correspondence confirms the accuracy and reliability of the upgraded G-DMRG code, bolstering confidence in its capacity to provide precise calculations of nuclear properties and dynamics. The successful validation serves as a critical step towards applying this advanced computational tool to increasingly complex nuclear systems and broadening its scope to investigate a wider range of phenomena in nuclear physics and beyond.
This computational approach distinguishes itself through a rigorous foundation in ab initio theory, meaning predictions arise directly from fundamental physical principles rather than empirical parameters. Crucially, the method employs realistic nuclear interactions derived from Chiral Interaction NNLO_{opt}, a sophisticated framework rooted in Quantum Chromodynamics. This interaction, determined from the fundamental constituents of matter, accurately describes the forces between nucleons – protons and neutrons – within the nucleus. By starting with these well-defined interactions, the calculations avoid adjustable parameters, offering a truly predictive capability for understanding nuclear behavior and providing insights into the properties of atomic nuclei with unprecedented accuracy.
The refinement of nuclear many-body methods has unlocked unprecedented capabilities in modeling complex nuclear systems, fostering a more complete and accurate understanding of nuclear structure, reactions, and astrophysical processes. By providing reliable predictions for the behavior of nuclei – from their ground state properties to their responses in various interactions – this advancement directly impacts fields like nuclear astrophysics. Accurate modeling of nuclear reactions is crucial for understanding the origin of elements in stars and supernovae, while detailed knowledge of nuclear structure informs the interpretation of experimental results and guides the search for new phenomena. This improved capability extends beyond terrestrial laboratories, offering insights into extreme astrophysical environments and the conditions prevailing in neutron stars and other compact objects, ultimately refining models of stellar evolution and nucleosynthesis.
The demonstrated success of the G-DMRG method paves the way for investigations into increasingly complex nuclear systems, exceeding the limitations of current computational techniques. Researchers intend to scale the method to accommodate larger numbers of nucleons, enabling a more detailed understanding of heavier nuclei and exotic nuclear structures. Beyond nuclear physics, the adaptability of the G-DMRG algorithm suggests potential applications in other many-body quantum systems, including condensed matter physics and quantum chemistry, where similar computational challenges arise in simulating complex interactions and emergent phenomena. This expansion promises to unlock new insights into the fundamental forces governing matter at its most basic level and could lead to advancements in diverse fields reliant on accurate quantum mechanical calculations.
The upgraded G-DMRG code underwent rigorous validation utilizing Helium-3 as a benchmark system, a crucial step in establishing its reliability and predictive power. This choice was strategic, as Helium-3 possesses a well-defined and extensively studied nuclear structure, allowing for direct comparison between G-DMRG calculations and established theoretical results. The validation process confirmed a high degree of accuracy, demonstrating the code’s ability to faithfully reproduce known properties of this light nucleus. This successful benchmark not only verifies the correctness of the implemented algorithms and approximations but also provides strong confidence in the method’s potential for tackling more complex nuclear systems and furthering the understanding of nuclear behavior.
The pursuit of elegant solutions in nuclear many-body problems feels perpetually Sisyphean. This work, refining the Gamow Density Matrix Renormalization Group method to capture broad resonances, is another attempt to tame the chaos. The researchers optimize reference spaces and truncation schemes, chasing precision in a realm where approximations are inherent. It’s a constant recalibration, recognizing that even the most sophisticated framework will eventually succumb to the complexities of production – in this case, the sheer number of interacting nucleons. As Albert Camus observed, “The struggle itself…is enough to fill a man’s heart. One must imagine Sisyphus happy.” This paper doesn’t promise a final answer, only a more refined tool for an endless, necessary struggle to understand the nucleus.
The Road Ahead
The refinement of Gamow Density Matrix Renormalization Group, as presented, predictably addresses existing limitations in calculating broad nuclear resonances. The optimization of reference spaces and truncation schemes is, of course, the perpetual task. Each improved algorithm merely postpones the inevitable: the point at which computational cost overwhelms diminishing returns, or the underlying approximations begin to visibly strain against the physics. The current work shifts the goalposts, but does not eliminate the game.
Future iterations will undoubtedly focus on expanding the accessible mass range. Yet, the real challenge isn’t scale; it’s the continued reliance on effective interactions. These interactions, calibrated to reproduce known data, embed prior knowledge – assumptions masquerading as solutions. The pursuit of truly ab initio calculations, divorced from empirical adjustments, remains largely aspirational. One suspects the next ‘breakthrough’ will simply be a more sophisticated method for hiding these dependencies.
Ultimately, the field appears to be solving increasingly complex versions of the same problem. The desire for a universally applicable, fundamentally accurate framework is understandable, but probably naive. It’s not that these calculations are incorrect; it’s that every elegant architecture eventually becomes a punchline, a testament to the limitations of any model attempting to capture the full complexity of quantum many-body systems. The goal isn’t fewer illusions; it’s a clearer understanding of what those illusions are masking.
Original article: https://arxiv.org/pdf/2601.16168.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Donkey Kong Country Returns HD version 1.1.0 update now available, adds Dixie Kong and Switch 2 enhancements
- How To Watch A Knight Of The Seven Kingdoms Online And Stream The Game Of Thrones Spinoff From Anywhere
- Ashes of Creation Rogue Guide for Beginners
- PS5’s Biggest Game Has Not Released Yet, PlayStation Boss Teases
- When to Expect One Piece Chapter 1172 Spoilers & Manga Leaks
- Sega Insider Drops Tease of Next Sonic Game
- Hytale: Upgrade All Workbenches to Max Level, Materials Guide
- New Netflix Movie Based on Hugely Popular Book Becomes An Instant Hit With Over 33M Hours Viewed
- Darkwood Trunk Location in Hytale
2026-01-24 09:43