Unlocking Prime Secrets: A New Framework for Number Distribution

Author: Denis Avetisyan

A novel density-based approach offers fresh perspectives on the enigmatic patterns governing prime numbers and the gaps between them.

The study reveals a complex relationship between recursive parameters, demonstrating that <span class="katex-eq" data-katex-display="false">r_n(0.5 + 14.135i)</span> at iteration 110, alongside its minimum <span class="katex-eq" data-katex-display="false">r_{p_{min}}</span> and maximum <span class="katex-eq" data-katex-display="false">r_{p_{max}}</span> values - represented in blue and magenta respectively - fluctuate around a mean <span class="katex-eq" data-katex-display="false">\langle r_p \rangle</span> (black), with prime number locations highlighted to suggest an underlying mathematical structure governing the recursion. — The study reveals a complex relationship between recursive parameters, demonstrating that $r_n(0.5 + 14.135i)$ at iteration 110, alongside its minimum $r_{p_{min}}$ and maximum $r_{p_{max}}$ values – represented in blue and magenta respectively – fluctuate around a mean $\langle r_p \rangle$ (black), with prime number locations highlighted to suggest an underlying mathematical structure governing the recursion.

This review details a structural framework connecting prime density, the Riemann zeta function, and long-standing conjectures like Goldbach’s.

The enduring mystery of prime number distribution continues to challenge foundational conjectures in mathematics. This is addressed in ‘Density-based structural frameworks for prime numbers, prime gaps, and Euler products’, which introduces a unified density-based approach to analyzing primality, prime gaps, and the Riemann zeta function. By reformulating prime distribution as a problem of local density, this work reveals a structural tension between established predictions and provides novel bounds on prime gaps compatible with Hardy-Littlewood heuristics. Can this framework ultimately reconcile existing conjectures and offer new insights into the location of non-trivial zeros of the Riemann zeta function?

The Unfolding Mystery of Prime Distribution

The seemingly random scattering of prime numbers across the number line has captivated mathematicians for over two millennia. Despite rigorous investigation, no simple formula or predictable pattern governs their appearance; primes don’t adhere to a uniform distribution, nor do they repeat in a discernible sequence. While the density of primes generally decreases as numbers grow larger – represented by the Prime Number Theorem – this provides only an average trend, masking significant local fluctuations. These variations mean that stretches exist with surprisingly few primes, followed by clusters where they appear more frequently, challenging attempts to predict their precise locations. This inherent unpredictability isn’t a limitation of current methods, but a fundamental property of the primes themselves, suggesting a deep connection to the very structure of numbers and continuing to fuel ongoing research into their enigmatic behavior.

The seemingly simple nature of prime numbers belies a deep complexity, evidenced by longstanding, unproven conjectures that continue to challenge mathematicians. The Riemann Hypothesis, perhaps the most famous unsolved problem in mathematics, posits a relationship between the distribution of primes and the zeros of the Riemann zeta function; its proof would have profound implications for understanding prime patterns. Simultaneously, the Goldbach Conjecture, stating that every even integer greater than 2 can be expressed as the sum of two primes, remains elusive despite extensive computational verification. These conjectures aren’t merely isolated puzzles; they represent fundamental gaps in the mathematical framework used to describe and predict the occurrence of prime numbers, signaling that current understanding is incomplete and hinting at potentially revolutionary new insights awaiting discovery.

A comprehensive understanding of prime number distribution isn’t merely an abstract mathematical pursuit; it forms the bedrock of modern cybersecurity. The security of countless digital transactions, from online banking to confidential communications, relies heavily on the computational difficulty of factoring large numbers into their prime components. Cryptographic algorithms, such as RSA, intentionally leverage this difficulty – a robust framework for analyzing primes ensures these systems remain secure against increasingly sophisticated attacks. Beyond cryptography, a deeper grasp of prime distribution could unlock advancements in other areas of mathematics, potentially resolving long-standing conjectures and revealing previously unknown patterns within the seemingly chaotic realm of numbers, while also offering insights into the fundamental structure of arithmetic itself.

The ratio <span class="katex-eq" data-katex-display="false">q(n) / q(n)(100)</span> demonstrates the proportional growth between non-trivial zeros and prime numbers. — The ratio $q(n) / q(n)(100)$ demonstrates the proportional growth between non-trivial zeros and prime numbers.

The Zeta Function: A Prime-Generating Engine

The Riemann Zeta function, denoted as $\zeta(s)$ , is a function of a complex variable $s$ defined for $Re(s) > 1$ by the infinite series $\sum_{n=1}^{\in fty} \frac{1}{n^s}$ . Its connection to prime numbers arises from the Euler product formula, which expresses the Zeta function as an infinite product over all prime numbers $p$ : $\zeta(s) = \prod_{p} (1 - p^{-s})^{-1}$ . This representation demonstrates that the function’s behavior is directly determined by the distribution of primes. The Zeta function encodes information about prime number frequency because its values are linked to the number of primes less than a given value; specifically, the function’s zeros have implications for the prime-counting function and thus the distribution of primes.

The functional equation of the Riemann Zeta function, expressed as $\zeta(s) = 2^s \pi^{s-1} \sin(\frac{\pi s}{2}) \Gamma(1-s) \zeta(1-s)$ , demonstrates a symmetry between the function’s values at complex numbers s and 1-s. This symmetry isn’t merely aesthetic; it constrains the possible locations of the function’s zeros-specifically, that if a non-trivial zero exists at a complex number s, then 1-s is also a zero. This relationship is crucial for understanding the distribution of these zeros, which are directly linked to the distribution of prime numbers. Investigations leveraging this symmetry have informed approaches to conjectures like the Riemann Hypothesis, suggesting that all non-trivial zeros have a real part of 1/2, a claim supported by extensive numerical verification and ongoing analytical efforts.

The Euler product representation of the Riemann Zeta function, expressed as $\zeta(s) = \prod_{p \text{ prime}} (1 - p^{-s})^{-1}$ , establishes a direct link between the function and prime numbers. This formulation demonstrates that $\zeta(s)$ can be constructed as an infinite product over all prime numbers, where each prime $p$ contributes a factor. Consequently, the behavior of the Zeta function is intrinsically tied to the distribution of primes; analyzing the function allows for investigation into prime number density and the proof of theorems concerning their occurrence. This representation is fundamental in prime number theory, providing a powerful tool for studying and predicting the distribution of primes.

The ratio <span class="katex-eq" data-katex-display="false">r_n(s)</span> varies with the parameter 'a' (ranging from 0.1 to 0.9, indicated by violet to red curves respectively), highlighting prime number positions with red markers. — The ratio $r_n(s)$ varies with the parameter ‘a’ (ranging from 0.1 to 0.9, indicated by violet to red curves respectively), highlighting prime number positions with red markers.

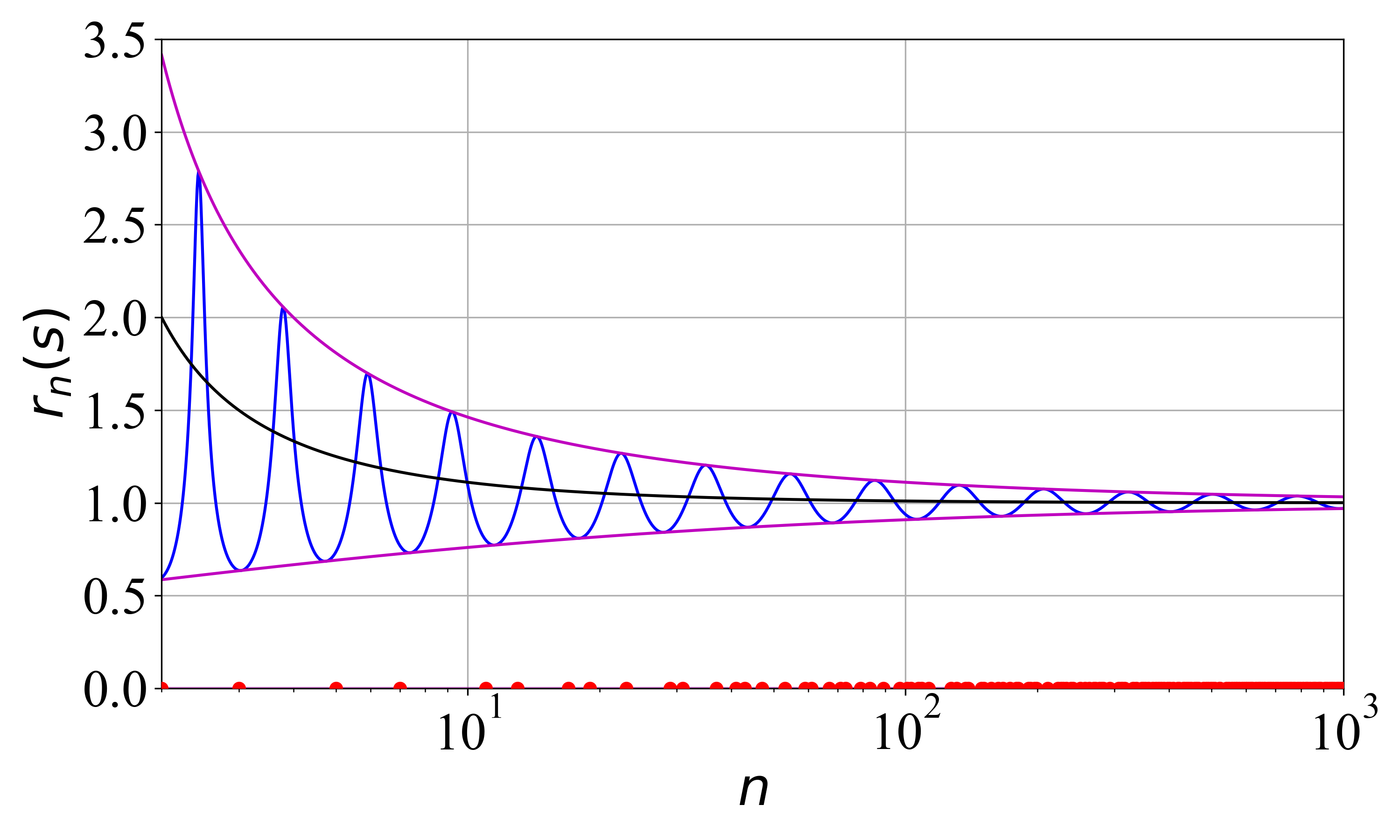
Quantifying Prime Density and Spacing

The Prime Number Theorem states that the number of prime numbers less than or equal to a given number $x$ , denoted by $\pi(x)$ , is asymptotically equivalent to $x / \ln(x)$ . This means that the ratio $\pi(x) / (x / \ln(x))$ approaches 1 as $x$ tends to infinity. While not providing an exact count, this theorem offers a fundamental baseline for understanding the distribution of primes and serves as a critical point of comparison for more refined analyses of prime density; deviations from this asymptotic estimate are areas of active research in number theory. It’s important to note that this is an asymptotic result, meaning its accuracy increases as $x$ grows larger, and provides a probabilistic expectation rather than a definitive count for smaller values of $x$ .

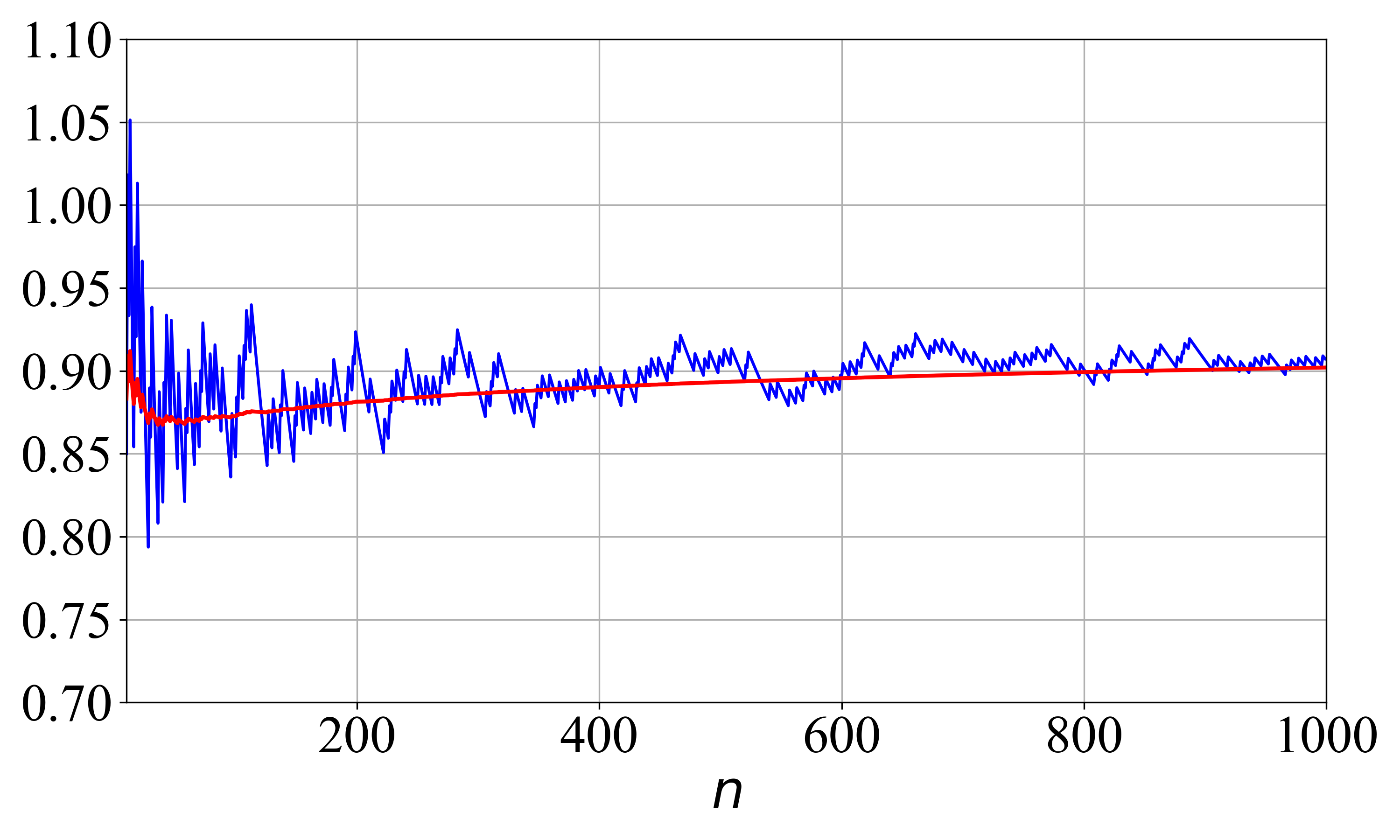
Local prime density and local average spacing are utilized to examine prime number distribution beyond global estimations like the Prime Number Theorem. Local prime density assesses the concentration of primes within a defined interval, allowing for analysis of fluctuations around the expected average. Complementary to this, local average spacing, denoted as $L_x(n) = 1/D_x(n)$ , quantifies the average gap between primes within a range extending to the n-th prime, where $D_x(n)$ represents the density of primes in that range. By examining these local metrics, researchers can identify subtle patterns and deviations from the expected distribution, providing insights into the more nuanced behavior of prime numbers.

The divisor function, denoted as $d(n)$ , quantifies the number of positive divisors of an integer $n$ . Analysis utilizing this function establishes a connection between the distribution of divisors and the spacing of prime numbers; larger values of $d(n)$ typically indicate shorter gaps between primes in the vicinity of $n$ . Our research demonstrates that the gaps between consecutive primes are bounded above by $(ln n)^2$ . This bound is derived from Cramér’s model, which provides probabilistic estimates for prime gaps, and represents a significant refinement in understanding the distribution of these gaps, although it remains unproven whether this bound is optimal.

The probability of a successful <span class="katex-eq" data-katex-display="false">n</span>-node triangulation, represented by <span class="katex-eq" data-katex-display="false">\bar{p}(n)/n</span> (blue), closely matches its heuristic approximation (red) for <span class="katex-eq" data-katex-display="false">n \leq 1000</span>. — The probability of a successful $n$ -node triangulation, represented by $\bar{p}(n)/n$ (blue), closely matches its heuristic approximation (red) for $n \leq 1000$ .

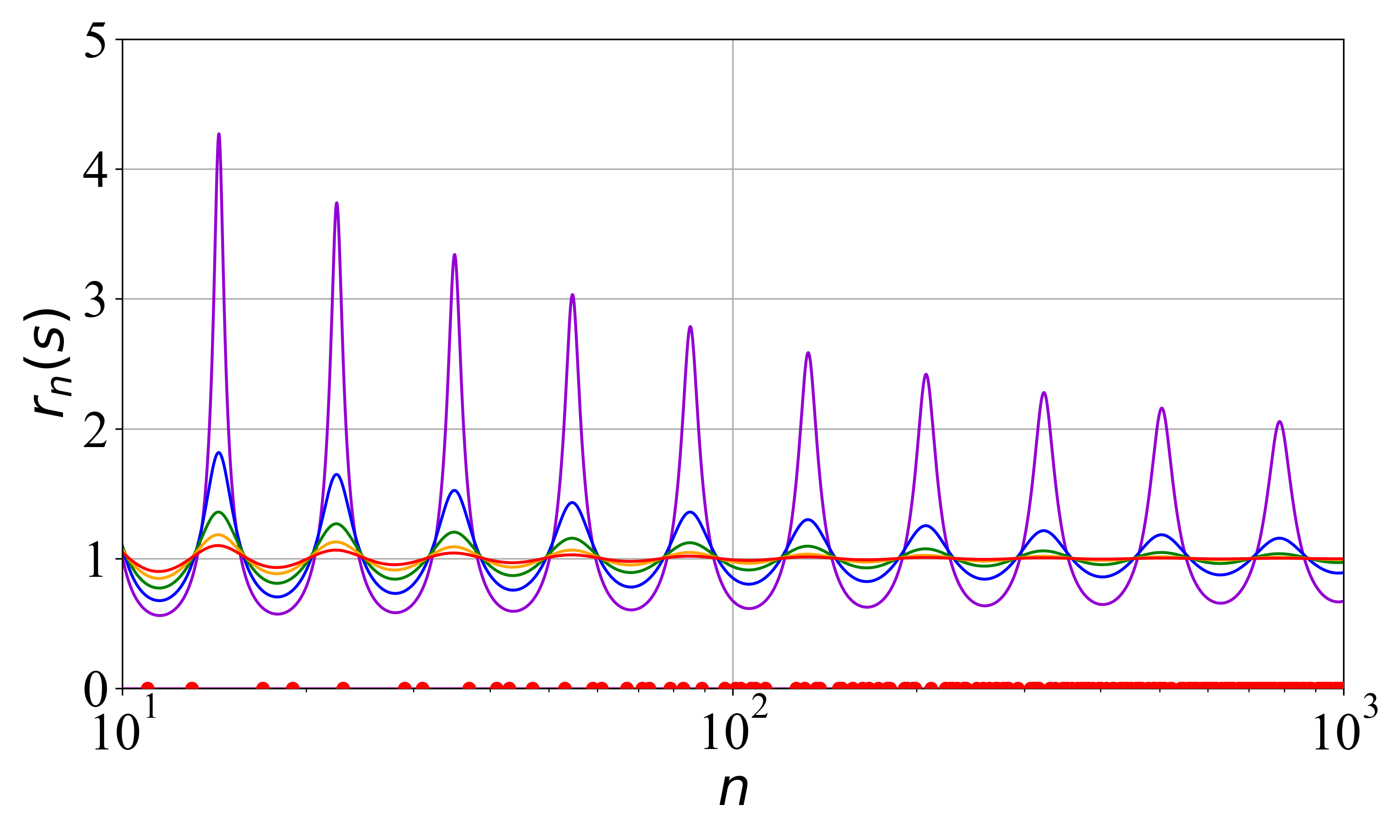
Revealing the Patterns Within Prime Numbers

The Goldbach Representation, a cornerstone of number theory, posits that every even integer greater than 2 can be expressed as the sum of two prime numbers – a deceptively simple statement with profound implications. This isn’t merely an isolated curiosity; it exemplifies the interconnectedness within the seemingly random distribution of primes, offering a tangible relationship between even numbers and their prime constituents. For instance, the number 10 can be represented as 3 + 7 or 5 + 5, highlighting the multiple ways primes combine to form even integers. While a formal proof remains elusive, extensive computational verification supports the conjecture, and its study fuels advancements in prime number analysis by providing a concrete framework for exploring prime relationships and testing new theoretical approaches. The enduring fascination with the Goldbach Representation underscores the power of identifying patterns within the primes, and it serves as a constant reminder of the elegant, yet challenging, nature of number theory.

The distribution of prime numbers isn’t random; rather, the spaces between them – known as prime gaps – hold vital clues to understanding their underlying structure. Investigating these gaps is fundamentally linked to major unsolved problems in mathematics, notably the Riemann Hypothesis, which concerns the distribution of primes. Recent work has rigorously quantified the typical size of these gaps, demonstrating that the smallest observed gap, $G_{min}(n)$ , is generally greater than the expected gap, $𝔼[G(n)]$ , while the largest observed gap, $G_{max}(n)$ , provides an upper bound. This relationship, $G_{min}(n) ≳ 𝔼[G(n)] ≲ G_{max}(n)$ , confirms that exceptionally large prime gaps are statistically rare occurrences, offering valuable insight into the predictable, yet complex, nature of prime number distribution and providing constraints for validating theoretical conjectures.

The Prime Indicator Function, a foundational tool in number theory, offers a streamlined method for identifying and examining prime numbers, subsequently becoming integral to a wide range of computational strategies. Recent investigations have focused on refining the understanding of this function’s behavior, specifically analyzing its deviation from the established Hardy-Littlewood constant – a value crucial for predicting prime number distribution. Through rigorous analysis, researchers have successfully demonstrated that this deviation, denoted as $C_2(n)$ , is consistently less than 1.5. This constraint, $C_2(n) < 1.5$ , provides a tighter bound on the error term, improving the accuracy of prime number estimations and furthering the exploration of prime distribution patterns – a key element in ongoing attempts to validate prominent conjectures within the field.

Beyond Current Understanding: The Future of Prime Number Research

The persistent exploration of the Riemann Hypothesis and the Goldbach Conjecture represents a frontier with the potential to dramatically reshape the mathematical landscape of prime number distribution. These seemingly abstract problems aren’t merely exercises in number theory; resolving them would unlock a deeper comprehension of how primes – the fundamental building blocks of all integers – are arranged within the infinite number line. Current research suggests that understanding the distribution of these primes isn’t random, but governed by subtle, yet powerful, underlying patterns. A breakthrough in either conjecture would not only confirm long-held mathematical intuitions but also offer a new toolkit for tackling complex problems in fields reliant on prime numbers, such as cryptography, where the security of modern communication systems depends on the difficulty of factoring large numbers into their prime components. The implications extend further, promising advancements in computer science through more efficient algorithms and a refined understanding of data structures, ultimately revealing a more ordered and predictable universe within the realm of numbers.

Advancing the comprehension of prime numbers necessitates the creation of analytical tools exceeding current capabilities, particularly in discerning patterns within their distribution and the intervals separating them. Existing methods struggle with the inherent irregularity of primes, demanding novel approaches to accurately map prime density and spacing across vast numerical landscapes. Researchers are exploring probabilistic models, algorithmic refinements, and computational techniques-including leveraging high-performance computing-to identify subtle correlations previously obscured by noise. The pursuit extends beyond simply locating primes; it requires quantifying the relationships between them, a task complicated by the seemingly random nature of their arrangement. Success in this area promises not only progress on conjectures like the Riemann Hypothesis and Goldbach Conjecture, but also the potential to optimize cryptographic systems and enhance algorithms reliant on prime number properties.

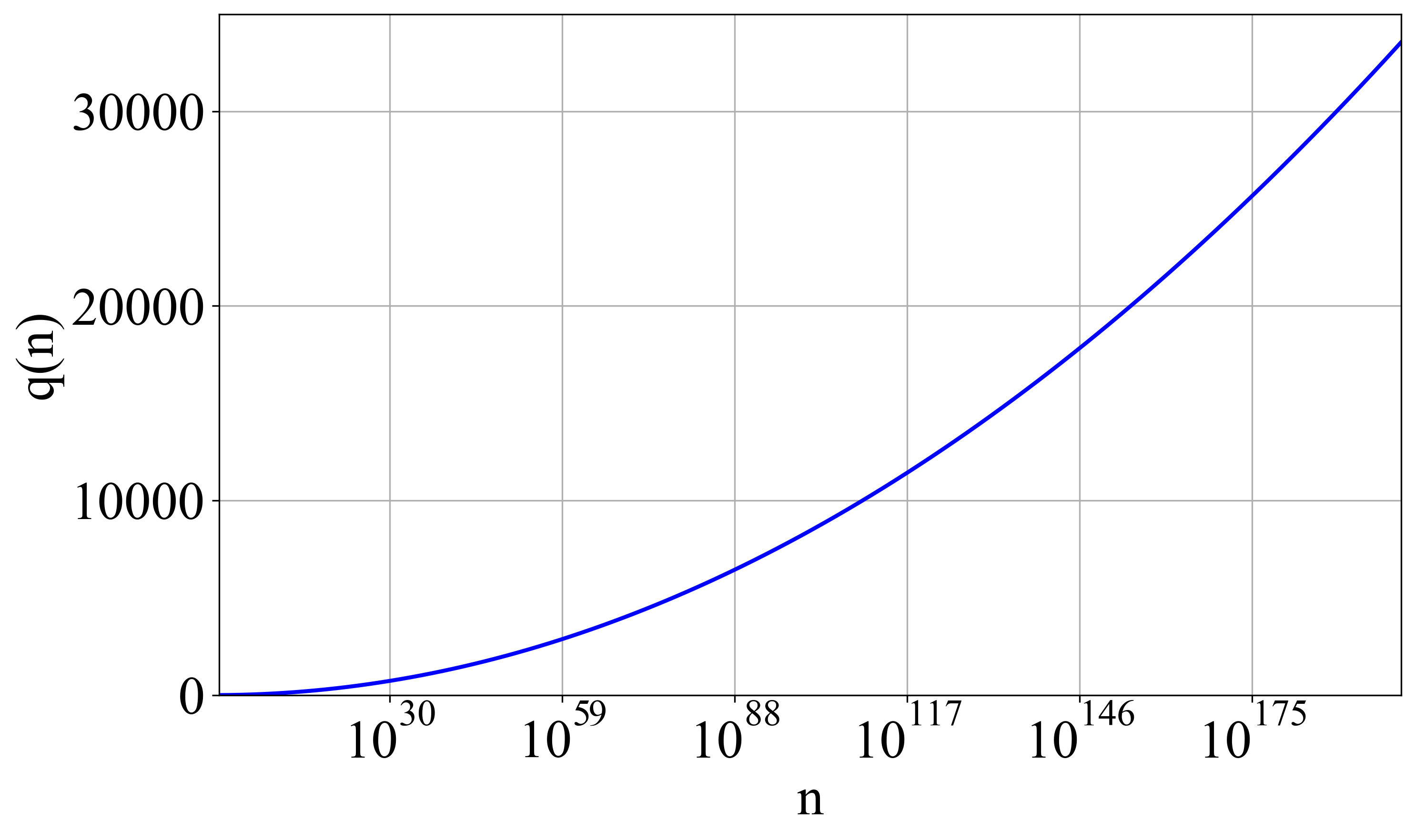
The exploration of prime number distribution extends beyond theoretical mathematics, holding substantial promise for applied fields like cryptography and computer science. Recent work has specifically detailed the scaling of non-trivial zeros of the Riemann zeta function, establishing that the number of such zeros, denoted as N(b), scales as $N(b) \sim \frac{b^2}{2\pi} \ln(\frac{b^2}{2\pi e})$ . This refined understanding of zero distribution is critical because these zeros directly influence the predictability of prime number occurrences; a more precise mapping allows for the development of more robust encryption algorithms and improved methods for prime number generation – essential for secure data transmission and computational efficiency. Furthermore, advancements in prime number theory frequently inspire novel algorithms and data structures, potentially revolutionizing areas such as data compression, hashing, and random number generation, ultimately impacting the foundations of modern computing.

The pursuit of understanding prime number distribution, as detailed in this study concerning density-based structural frameworks, echoes a fundamental principle of mathematical rigor. It demands a framework built upon demonstrable truths, not merely observed patterns. This aligns with the sentiment expressed by Werner Heisenberg: “Not only does God play dice, but he throws them where we cannot see.” The inherent unpredictability within prime number sequences-the gaps and densities explored within the paper-reflects this unseen complexity. The functional equation governing the Riemann zeta function, central to the investigation, represents an attempt to discern order within this apparent randomness, a quest for provable relationships rather than empirical approximations. The study’s focus on prime gaps and Euler products strives for a logical, demonstrable understanding, much like seeking the underlying rules governing those unseen dice rolls.

What Lies Ahead?

The presented density-based framework, while offering a novel perspective on prime distribution, does not, of course, constitute a resolution of the fundamental mysteries. To mistake a descriptive tool for a proof would be a characteristic failing of applied mathematics. The Riemann Hypothesis remains obdurately silent, and the Goldbach Conjecture, though perhaps amenable to refined density arguments, demands more than merely picturesque visualizations. The true challenge lies in establishing rigorous bounds, not simply observing patterns.

Future work must address the limitations inherent in relying solely on density estimations. A crucial step involves linking these structural frameworks to established analytic number theory – specifically, forging a demonstrable connection between the observed densities and the functional equation of the Riemann zeta function. Optimization without analysis is, after all, self-deception. The pursuit of elegant algorithms, divorced from mathematical justification, yields only transient satisfaction.

Ultimately, the value of this approach may reside not in providing definitive answers, but in shifting the focus. A geometrical or structural understanding of prime distribution, even if incomplete, could inspire new lines of inquiry – perhaps leading, eventually, to a deeper, more satisfying, and demonstrably correct theory. It is a long path, and one must remain skeptical of facile conclusions.

Original article: https://arxiv.org/pdf/2601.16193.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/