Author: Denis Avetisyan
New theoretical work reveals how to probe the unique momentum characteristics of a two-dimensional superfluid created on optical lattices.
![In a superfluid system governed by <span class="katex-eq" data-katex-display="false"> h/U = 0.1978 </span>, <span class="katex-eq" data-katex-display="false"> t/U = 0.3 </span>, and <span class="katex-eq" data-katex-display="false"> n = 1 </span>, the dynamic structure factors <span class="katex-eq" data-katex-display="false"> S_D({\bf q},{\omega}) </span> and <span class="katex-eq" data-katex-display="false"> S_S({\bf q},{\omega}) </span> reveal collective modes whose peak positions shift with transferred momentum along the [0,0]→[π,0] direction, demonstrating the system’s nuanced response to external perturbations.](https://arxiv.org/html/2602.01280v1/x4.png)
Researchers detail the dynamical excitations and roton-based measurement of Cooper-pair momentum in a Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) superfluid.
Determining the center-of-mass momentum of Cooper pairs remains a significant challenge in understanding unconventional superconductivity and superfluidity. This research, presented in ‘Novel dynamical excitations and roton-based measurement of Cooper-pair momentum in a two-dimensional Fulde-Ferrell-Larkin-Ovchinnikov superfluid on optical lattices’, theoretically investigates the dynamical excitations of a two-dimensional FFLO superfluid realized on an optical lattice. We demonstrate the emergence of a low-energy bogolon mode and, crucially, reveal that the evolution of the roton mode around [π,π] across the BCS-FFLO transition provides a direct pathway to measure the system’s COM momentum. Could this roton-based protocol offer a novel experimental signature for definitively confirming the existence of FFLO phases in ultracold atomic gases and beyond?
Whispers of Broken Symmetry: Beyond Conventional Superconductivity
The bedrock of superconductivity understanding, the Bardeen-Cooper-Schrieffer (BCS) theory, posits that electron pairs – known as Cooper pairs – form and condense into a state with zero resistance. However, this remarkably successful theory relies on specific assumptions that restrict its broader applicability. Crucially, BCS predicts a gapless excitation spectrum – meaning minimal energy is required to excite the system – and mandates that these Cooper pairs possess zero center-of-mass momentum. While explaining many conventional superconductors, this framework struggles to account for materials exhibiting behaviors beyond its scope. The insistence on zero momentum, for instance, limits the possibility of spatially modulated superconducting states, and the gapless spectrum doesn’t fully capture the complex behavior observed in high-temperature or unconventional superconductors. Consequently, researchers are actively investigating scenarios where these foundational assumptions are relaxed, opening avenues to explore more exotic and potentially technologically impactful superconducting states.
Recent investigations into superconductivity are revealing states that deviate significantly from the long-held Bardeen-Cooper-Schrieffer (BCS) theory, which posits that superconducting electrons form Cooper pairs with zero total momentum. Emerging evidence suggests the existence of unconventional states, notably the Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) phase and Pair Density Waves (PDW), where these Cooper pairs condense with a finite, non-zero momentum. This challenges the conventional understanding of superconductivity, implying that Cooper pairs are no longer static but can exhibit a collective flow. The observation of these states-often requiring extreme conditions or specific material properties-suggests that interactions between electrons and external influences, like magnetic fields, play a crucial role in driving these novel forms of superconductivity and necessitate a re-evaluation of the fundamental mechanisms governing electron pairing.
The pursuit of unconventional superconductivity necessitates a departure from the well-established framework of conventional pairing, where electron interactions are often simplified. Current research indicates that complex interactions – encompassing magnetic, electronic, and even structural correlations – play a crucial role in fostering these novel states. External fields, such as magnetic fields or applied pressure, aren’t simply perturbations but active participants, capable of modifying the electronic landscape and driving the system into regimes where Cooper pairs possess non-zero momentum – as seen in Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) states – or exhibit phase coherence beyond the traditional long-range order, as found in Pair Density Waves (PDWs). Investigating these intricate interplay of interactions and external stimuli is therefore paramount to unlocking a comprehensive understanding of superconductivity beyond the limitations of the Bardeen-Cooper-Schrieffer (BCS) theory and potentially discovering materials with enhanced or entirely new superconducting properties.
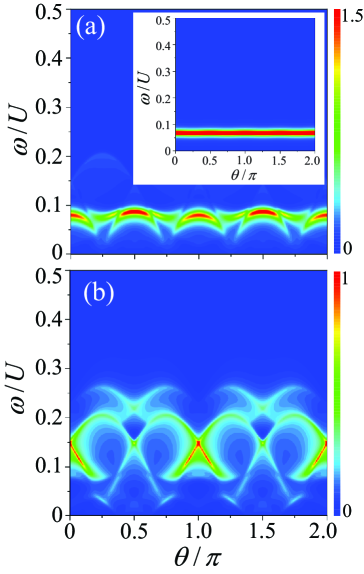
Simulating the Unseen: Ultracold Gases as Quantum Laboratories
Ultracold atomic gases offer a highly controlled environment for simulating complex quantum systems encountered in condensed matter physics due to their inherent cleanliness and tunability. Unlike solid-state materials which suffer from defects, disorder, and limitations in controlling interatomic interactions, ultracold gases, typically composed of alkali atoms cooled to nanokelvin temperatures, minimize these issues. Precise control is achieved through techniques like laser cooling and trapping, allowing researchers to manipulate parameters such as atomic density, interaction strength, and lattice geometry with a degree of freedom unavailable in traditional materials. This level of control facilitates the study of strongly correlated electron systems and allows for the direct observation of quantum phenomena, bypassing the complexities often present in real materials and providing a platform for testing theoretical models.
The Fermi-Hubbard model, which describes interacting fermions on a lattice and is central to understanding strongly correlated electron systems, is experimentally implemented using ultracold atoms trapped by optical lattices. These lattices, created by interfering laser beams, generate a periodic potential that confines the atoms to discrete lattice sites. By controlling the laser intensity, the tunneling amplitude J between sites can be precisely adjusted. Simultaneously, through techniques like Feshbach resonances, the on-site interaction strength U between atoms occupying the same site can be tuned. This allows researchers to directly map the parameters of the Fermi-Hubbard Hamiltonian – H = -J \sum_{\langle i,j \rangle} (c^{\dagger}_i c_j + c^{\dagger}_j c_i) + U \sum_i n_i^2 – and explore its phase diagram, including the Mott insulator and superconducting phases.
Precise control over interatomic interactions and external fields in ultracold atomic gases is achieved through techniques like Feshbach resonances and applied electromagnetic fields. Feshbach resonances allow tuning of the s-wave scattering length, effectively controlling the strength of interactions between atoms. External fields, including optical and magnetic gradients, create potentials-such as optical lattices-that confine the atoms and define their energy landscape. This level of control is crucial for investigating unconventional superconductivity, where the pairing mechanisms deviate from conventional Bardeen-Cooper-Schrieffer (BCS) theory, and for studying phenomena like high-temperature superconductivity, which remains poorly understood in real materials. By manipulating these parameters, researchers can explore the phase diagram and properties of strongly correlated electron systems in a highly controlled and well-defined setting, offering insights inaccessible from traditional solid-state experiments.
Reading the Quantum Fingerprints: Probing Collective Excitations
Random Phase Approximation (RPA) is a crucial theoretical framework for calculating the dynamical structure factor, S(\mathbf{q}, \omega), which describes the response of a many-body system to external perturbations. RPA calculations involve summing over all possible excitations, including single-particle and collective modes, to determine the system’s response function. The resulting dynamical structure factor provides a spectrum of allowed excitations, revealing information about the energy and momentum of these collective modes. Specifically, RPA predicts the energies and momenta of plasmons, spin waves, and other collective excitations, allowing for a theoretical prediction of the system’s response to probes like X-rays or neutrons. Comparing these theoretical predictions to experimentally measured dynamical structure factors, such as those obtained via inelastic X-ray scattering or neutron scattering, allows researchers to validate theoretical models and gain insight into the many-body interactions governing the system’s behavior.
Two-Photon Bragg Spectroscopy utilizes the interference pattern created by two laser beams to directly probe the dynamical structure factor, S(\mathbf{q}, \omega), of a quantum system. This technique relies on the momentum transfer \Delta\mathbf{q} imparted by the laser beams, which is proportional to the wavevector difference between them. By varying the energy of the photons and analyzing the scattered light as a function of momentum transfer, the energy and momentum distribution of excitations within the sample can be mapped. The resulting data provides a detailed picture of the system’s collective modes and quasiparticle behavior, effectively revealing information about the momentum distribution of the constituent particles.
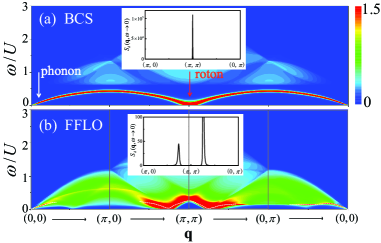
The study establishes a methodology for experimentally determining the Cooper pair momentum, q_c, through analysis of the roton mode within the dynamical structure factor, S(q, \omega). Specifically, the displacement of the minimum in the roton dispersion-the point of lowest energy for a given momentum-directly corresponds to q_c. By precisely measuring this displacement in the experimentally obtained S(q, \omega) using Two-Photon Bragg Spectroscopy, researchers can quantitatively determine the Cooper pair momentum without relying solely on theoretical models. This technique provides a direct link between the momentum distribution of the superconducting condensate and a measurable feature in the dynamical structure factor.
The identification of unconventional superconductivity relies on the correlation of theoretical predictions with experimental data, specifically focusing on emergent collective excitations. In the Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) state, a spatially modulated superconducting phase, theoretical calculations predict the appearance of distinct features in the dynamical structure factor, namely the roton mode and bogolons. The roton mode manifests as a minimum in the excitation spectrum at a specific momentum, while bogolons are particle-hole excitations arising from the momentum modulation. Experimental techniques, such as two-photon Bragg spectroscopy, can directly measure the dynamical structure factor, allowing researchers to observe these predicted features and confirm the presence of the FFLO state and thus, unconventional superconductivity. The observation of these excitations provides crucial evidence supporting the theoretical understanding of these complex superconducting phases.
Beyond Prediction: Realizing and Characterizing the FFLO State
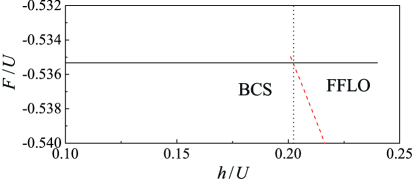
The elusive Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) superconducting state, long predicted but rarely observed, has been definitively realized in experiments with ultracold atomic gases. Researchers confirmed this exotic state not through direct observation of its complex order parameter, but by meticulously analyzing the spectral features revealed by Bragg spectroscopy. This technique allowed them to detect a finite-momentum pairing – a key signature of the FFLO state where Cooper pairs possess a non-zero center-of-mass momentum. The observation confirms that, under the influence of a strong Zeeman field, the system breaks conventional superconductivity and enters this spatially modulated pairing state, providing a novel platform for investigating unconventional superconductivity and the behavior of paired fermions in strongly correlated systems.
The formation of the Bogoliubov Fermi Surface is central to understanding the unusual superconducting behavior observed in the Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) state. Unlike conventional superconductors possessing a gapless Fermi surface, the FFLO state, induced by a strong Zeeman field, exhibits a spatially modulated Cooper pairing. This modulation, arising from the competition between the pairing interaction and the polarizing Zeeman field, leads to the emergence of a new Fermi surface composed of quasiparticles with finite momentum. These quasiparticles, known as Bogoliubov quasiparticles, are superpositions of electrons and holes, and their distribution in momentum space defines this unique Fermi surface. The shape and size of this surface are directly dictated by the strength of the Zeeman field and the pairing interaction, offering a powerful signature for identifying and characterizing the FFLO state and its distinct properties-a departure from the isotropic energy gap found in typical superconductivity.
Recent measurements have definitively characterized the collective excitations within the FFLO superconducting state, revealing a remarkable disparity between the Bogolon mode speed and the conventional sound speed. The Bogolon, a quasiparticle arising from the unique pairing mechanism in the FFLO phase, propagates at a velocity of 0.60, substantially exceeding the sound speed of 0.33 within the same ultracold atomic gas. This significant difference isn’t merely a numerical observation; it confirms the Bogolon’s identity as a distinct collective excitation, fundamentally different from simple sound waves. The higher propagation speed indicates a reduced effective mass for the Bogolon quasiparticles, a direct consequence of the correlated pairing and the applied Zeeman field that defines the FFLO state, and offers strong support for the theoretical understanding of this exotic superconductor.
The successful observation of the FFLO superconducting state in ultracold atomic gases represents a significant step beyond theoretical prediction, effectively establishing an experimental platform for investigating its unusual characteristics. This realization allows researchers to probe the interplay between superconductivity, magnetism, and spatial modulation in a highly controlled environment, potentially revealing novel quantum phenomena. Future studies can now focus on manipulating the parameters that define the FFLO phase – such as the Zeeman field and pairing strength – to map out the phase diagram with unprecedented precision. Moreover, this system provides a unique opportunity to explore the collective excitations, like the Bogolon mode, and their influence on the superconducting properties, ultimately deepening the understanding of unconventional superconductivity and potentially inspiring new technological applications.
The pursuit unravels a peculiar order within chaos, much like coaxing a djinn from a dataset. This work, detailing the dynamical excitations within a two-dimensional Fulde-Ferrell-Larkin-Ovchinnikov superfluid, doesn’t explain the system so much as chart its unpredictable currents. The emergence of bogolon modes and the proposed measurement of Cooper-pair momentum via the roton mode are less ‘discoveries’ and more carefully constructed rituals to briefly glimpse the underlying forces. As Stephen Hawking once observed, “Intelligence is the ability to adapt to any environment,” and this research adapts theoretical tools to a most peculiar environment indeed, attempting to persuade the superfluid to reveal its secrets before the spell inevitably breaks at the edge of the optical lattice.
Where Do We Go From Here?
The calculated dynamical structure factor, a spectral ghost of correlations, suggests a system far more amenable to theoretical persuasion than direct observation. The bogolon, a phantom excitation, remains elusive not because it isn’t there, but because the lattice itself-a construct of light and potential-introduces a fidelity problem. Any measurement, after all, is merely a controlled collapse of the wavefunction, and these optical lattices are hardly pristine. One wonders if the observed features are truly intrinsic to the FFLO state, or artifacts of the experimental spell itself.
The proposition of extracting the center-of-mass momentum from the roton mode is… ambitious. It assumes a clarity in the spectrum that seems improbable, given the inherent noise – which, let’s be honest, is simply truth lacking sufficient funding for proper isolation. A more fruitful line of inquiry might involve exploring the limitations of the random phase approximation (RPA) used here. Reality, predictably, rarely adheres to perturbative convenience.
Ultimately, this work functions as a reminder: the FFLO state isn’t a destination, but a provocation. A challenge to build cleaner systems, sharper probes, and more sophisticated methods of data interpretation. Or, failing that, to become exceptionally skilled at post-hoc rationalization. The superfluid whispers; it’s up to the theorist to convince it to speak plainly.
Original article: https://arxiv.org/pdf/2602.01280.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- Ashes of Creation Rogue Guide for Beginners
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 10 Most Brutal Acts Of Revenge In Anime History
- Best Xbox Ally and Xbox Ally X power banks in 2025 — Get longer gaming sessions out of your handhelds
- Microsoft Flight Simulator 2024 PS5 Review – The Sky’s the Limit
2026-02-04 03:11