Author: Denis Avetisyan
A new analysis of pion-proton collisions sheds light on the inner workings of the Λ(1405) and Λ(1520) hyperons.
Researchers employ an effective Lagrangian approach and explore constituent counting rules to investigate the production mechanisms of these key particles in exclusive reactions.
The internal structure of hyperon resonances remains a persistent challenge in hadron spectroscopy, particularly concerning the nature of the \Lambda(1405) and \Lambda(1520). This study, ‘Producing $Λ(1405)$ and $Λ(1520)$ in $π^-p$ reaction to explore their inner structures’, investigates the production mechanisms of these states in \pi^- p scattering via an effective Lagrangian approach incorporating Regge trajectories and exchange contributions. Our analysis reveals distinct production dynamics for each resonance-u-channel dominance for \Lambda(1405) and t-channel dominance for \Lambda(1520)-suggesting a more exotic configuration for the former, while also demonstrating the experimental feasibility of reconstructing the \Lambda(1520) via the K\pi\Sigma final state; could future high-precision measurements at facilities like AMBER and J-PARC further elucidate the structural properties and reaction mechanisms of these intriguing baryons?
Unveiling the Anomalous Lambda(1405): A Challenge to Conventional Understanding
The Lambda(1405) hyperon consistently challenges established understandings of particle composition. Unlike most baryons, which neatly fit within the quark model – a framework describing hadrons as combinations of three quarks – the Lambda(1405) exhibits properties that deviate significantly from predictions. Its unexpectedly low mass and unusual decay patterns suggest its internal structure is far more intricate than a simple three-quark arrangement. Researchers propose possibilities ranging from a five-quark configuration – an exotic state known as a pentaquark – to a surprisingly tightly bound molecule composed of a meson and a baryon. Determining the true nature of the Lambda(1405) isn’t merely about classifying a single particle; it’s about refining the fundamental rules governing how matter assembles at the subatomic level, potentially revealing limitations in current theoretical frameworks and opening doors to a richer, more nuanced understanding of the strong force.
The Lambda(1405) hyperon consistently challenges the predictions of established hadron spectroscopy. Existing theoretical frameworks, built upon the quark model and its extensions, struggle to accurately reproduce the particle’s observed mass and the patterns in how it decays into other particles. Attempts to categorize the Lambda(1405) within conventional spectroscopic schemes consistently yield discrepancies, suggesting that its internal structure and interactions are more nuanced than previously understood. This persistent mismatch between experimental data and theoretical predictions has prompted physicists to explore innovative approaches, including models that posit the Lambda(1405) as a more exotic state – potentially a five-quark configuration or a tightly bound composite of a meson and a baryon – demanding a re-evaluation of fundamental principles governing hadron composition and strong force dynamics.
The Lambda(1405) hyperon stands as a compelling enigma in particle physics, demanding a reevaluation of conventional understandings of how matter is assembled. Current theoretical frameworks, largely based on the quark model, struggle to account for its observed characteristics, prompting speculation that it isn’t simply a three-quark baryon. Instead, the Lambda(1405) may represent an exotic five-quark state – a pentaquark – or, alternatively, a remarkably tightly bound molecule consisting of a meson and a baryon acting as a single entity. Determining its true composition is paramount, as confirmation of either scenario would necessitate significant revisions to the established theory of hadron composition and provide crucial insights into the strong force governing interactions within atomic nuclei, potentially revealing previously unknown facets of matter’s fundamental building blocks.
Probing Hadron Interactions: The Role of Pi-p Scattering
Pi-p (pion-proton) scattering is utilized as a primary method for investigating the strong force interactions and internal structure of hadrons, particularly resonant baryons such as the Lambda(1405) and Lambda(1520). This technique involves observing the scattering of pions off protons, and analyzing the resulting angular distributions and reaction rates – the total and differential cross sections – to infer the properties of intermediate hadronic states. The characteristics of these scattering events provide information about the masses, spins, parities, and decay modes of these resonances, effectively allowing physicists to map out the spectrum of excited baryonic states and test the predictions of various theoretical models of hadron structure.
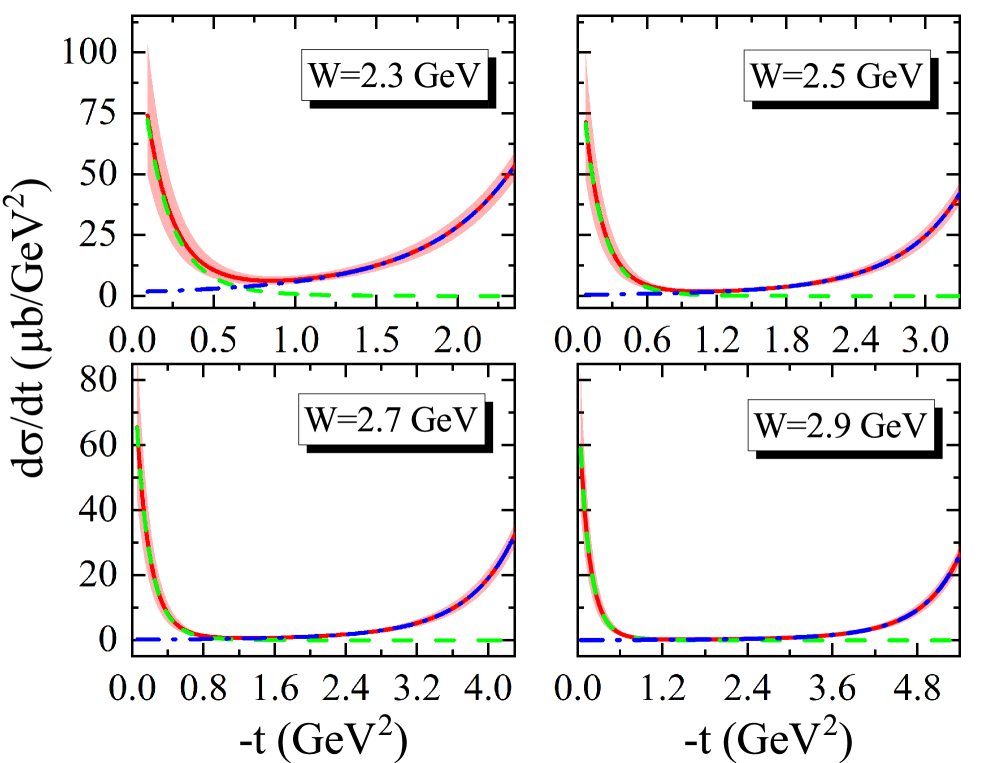
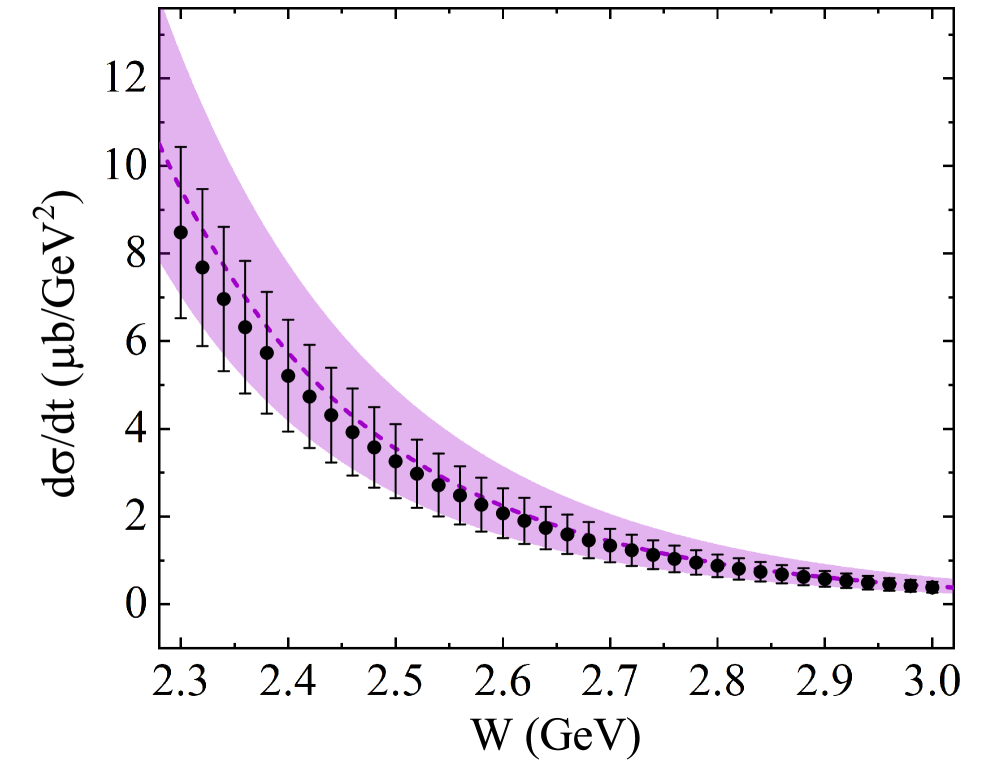
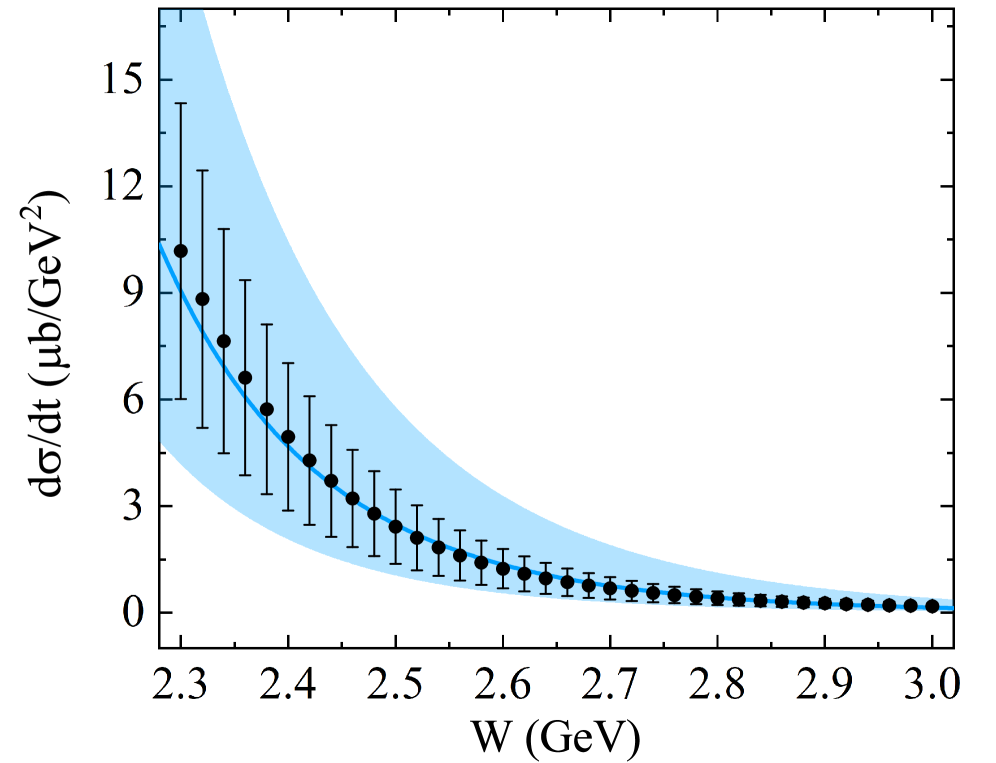
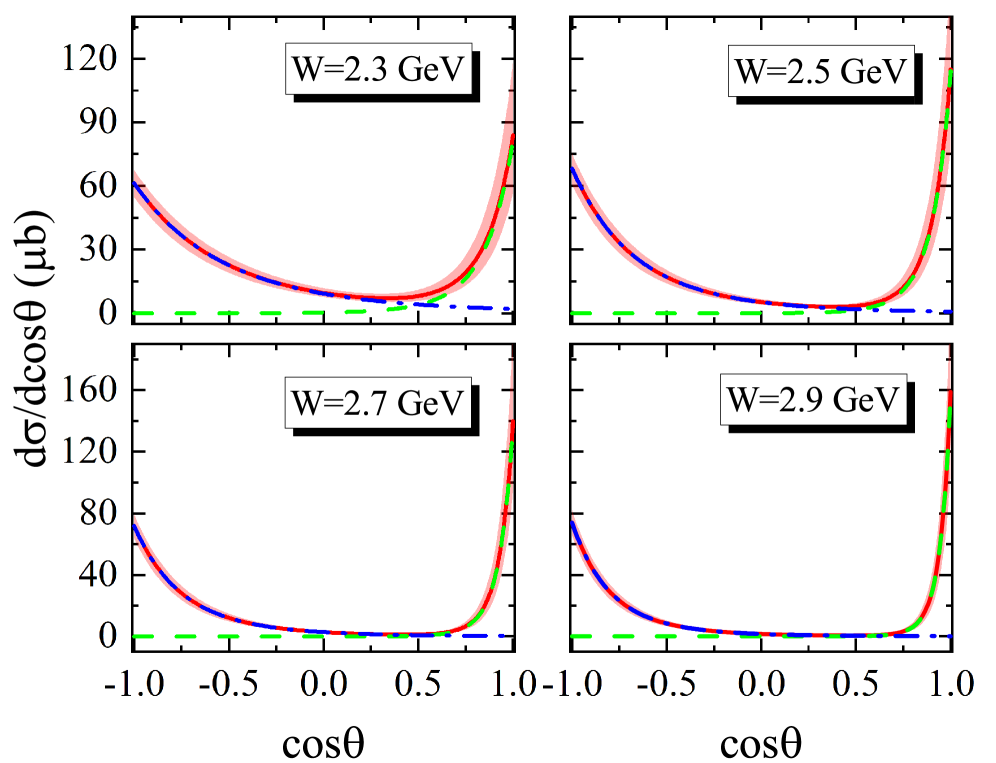
Analysis of total and differential cross sections derived from pion-proton (π⁻p) scattering provides a method for identifying and characterizing resonant states of hadrons. Theoretical calculations predict the Λ(1520) resonance is detectable via π⁻p scattering with a cross section of at least 494.34 μb/GeV. This value represents a threshold for experimental verification, indicating a statistically significant signal is expected within the parameters of current and planned experiments. The measured cross section, combined with angular distributions, allows for the determination of key properties of the Λ(1520), including its mass, width, and spin-parity assignment.
The Λ1520 baryon, characterized as a conventional spin-orbit excited state, provides a critical point of reference for analyzing the properties of the Λ1405, which exhibits anomalous behavior not fully explained by standard quark models. Comparative analysis leverages the well-defined characteristics of the Λ1520 to highlight the deviations observed in the Λ1405. Calculations demonstrate a feasible detection cross section for the Λ1405 in π–p scattering, estimated to be greater than or equal to 381.97 μb/GeV, supporting its experimental investigation and detailed study alongside the Λ1520.
Beyond Perturbation: Effective Lagrangians and Meson Exchange
The Effective Lagrangian approach addresses limitations of perturbative Quantum Chromodynamics (QCD) in describing hadron interactions by focusing on the relevant degrees of freedom at a given energy scale. Instead of directly solving the full QCD equations, which are computationally intractable, this method constructs a Lagrangian – a mathematical function describing the system’s dynamics – incorporating only the necessary hadrons and their interactions. This allows for calculations of scattering amplitudes and decay rates that would be impossible with purely perturbative methods, particularly in the low-energy regime where perturbative expansions fail. The Lagrangian includes terms representing the exchange of virtual particles mediating the strong force, and its parameters are determined by fitting to experimental data or through more fundamental QCD calculations when possible. This approach enables the systematic study of hadron dynamics and the prediction of observable quantities without requiring a complete understanding of the underlying QCD dynamics at all energy scales.
The strong nuclear force between hadrons is not solely a direct interaction, but is significantly mediated by the exchange of mesons. Specifically, Sigma (Σ) and K (K</i>) mesons play a critical role in modeling this force. Sigma exchange primarily contributes to short-range attraction between baryons, while K exchange introduces both attractive and repulsive components, influencing the medium-range interactions. Analysis of hadron scattering cross-sections, particularly in processes involving strange baryons, demonstrates the necessity of including these exchange terms to accurately reproduce experimental data. The strength and relative contributions of Sigma and K exchange are determined by fitting theoretical models to observed scattering amplitudes, allowing for a quantitative understanding of the underlying strong force dynamics.
The construction of effective Lagrangians allows for the systematic inclusion of meson exchange processes, such as Σ and K^* exchange, which contribute to the interaction potential between baryons. By parameterizing the couplings and masses within the Lagrangian, calculations can reproduce the observed binding energies and decay modes of resonance states like the \Lambda(1405) . Specifically, the \Lambda(1405) is understood as a pole arising from the coupled \bar{K}N and \pi \Sigma channels, and the Lagrangian formalism accurately predicts its pole position and wavefunction mixing. Further refinement of the Lagrangian, incorporating higher-order terms and additional exchange mesons, improves predictions for other excited baryons and their associated properties, offering a pathway to a more complete understanding of hadron structure.
Refining the Framework: Reggeization and Constituent Counting
The Reggeized Trajectory Model represents a significant refinement of the Effective Lagrangian Approach to understanding particle interactions. By incorporating Regge poles – theoretical constructs representing resonant states that appear in high-energy scattering – the model achieves a more precise description of how scattering amplitudes change with energy. Unlike simpler models that treat particles as point-like, this approach acknowledges the internal structure of hadrons and the exchange of momentum via these resonant states. This allows for a more realistic representation of the energy dependence observed in experiments, particularly at higher energies where the internal structure becomes more prominent. The inclusion of Regge poles effectively ‘smooths’ the energy dependence, accounting for the broadening of resonant peaks and providing a more accurate prediction of scattering behavior across a wider energy range, thereby improving the model’s predictive power and its ability to connect theoretical calculations with experimental observations.
The Constituent Counting Rule offers a powerful method for validating theoretical models of hadron interactions by directly connecting observable scattering behavior to the internal composition of particles. This rule posits a predictable relationship between the total cross-section of hadronic collisions and the number of constituent quarks and antiquarks within the colliding hadrons; as energy increases, cross-sections are expected to decrease with a power law determined by this constituent count. Specifically, the rule predicts that hadrons composed of more constituents will exhibit a faster fall-off in cross-section with increasing energy. By meticulously analyzing experimental data on hadronic scattering, researchers can extract scaling exponents and compare these values to predictions based on various models, providing a crucial independent check on their validity and offering insights into the complex internal structure of these particles.
A unified analysis leveraging Reggeized trajectories and constituent counting offers a compelling description of the excited baryon states Lambda(1405) and Lambda(1520). This approach reveals that Lambda(1520) adheres to a scaling exponent of 10, a characteristic strongly indicative of a conventional three-quark baryon structure. However, Lambda(1405) diverges from this pattern, exhibiting a scaling exponent of 8. This deviation suggests a more intricate composition for Lambda(1405), potentially involving quark-antiquark pairs or other exotic configurations that extend beyond the simple three-quark model, providing valuable clues about the complex internal dynamics of these particles and challenging established understandings of baryon structure.
Beyond Description: Implications for Hadron Physics and the Future of Understanding
Investigations into the Lambda(1405) and Lambda(1520) baryons extend far beyond merely cataloging exotic particles; they offer a unique window into the intricacies of the strong force-one of the four fundamental forces governing the universe. These baryons, possessing unusual quantum numbers and decay characteristics, challenge conventional understandings of hadron structure and the mechanisms by which quarks and gluons bind together. Detailed analyses of their properties, including their mass, spin, and decay modes, provide critical tests for theoretical models like chiral symmetry breaking and the role of meson-baryon interactions. Consequently, a deeper comprehension of these excited states not only refines the standard quark model but also potentially reveals limitations in current theoretical frameworks and opens doors to a richer, more nuanced understanding of the strong force’s behavior at the energy scales relevant to the formation of matter in the early universe and within neutron stars, furthering the quest to define the fundamental constituents of matter itself.
The Dalitz process, a photoproduction reaction involving a real photon inducing the decay of a neutral pion into a positron and electron pair, serves as a valuable and independent means of scrutinizing the decay dynamics of excited hyperons like the Lambda(1405) and Lambda(1520). Unlike many traditional decay measurements which rely on detecting final-state hadrons, the Dalitz process is sensitive to the electromagnetic properties and internal quantum numbers of these baryons. By precisely measuring the energy and angular distribution of the emitted electron-positron pairs, researchers can effectively map the decay amplitudes and constrain the possible internal configurations of these states – distinguishing between various theoretical models predicting their composition and structure. This complementary approach, which probes the excited states through electromagnetic interactions rather than strong force decays, provides crucial validation for interpretations derived from hadronic decay studies and strengthens the overall understanding of baryon spectroscopy and the underlying strong interaction.
Ongoing investigations are poised to enhance current theoretical frameworks by meticulously refining the models used to describe the Lambda(1405) and Lambda(1520). This includes exploring the subtle interplay between these exotic baryons and other facets of hadron physics, such as the search for other resonance states and a deeper understanding of quark-gluon dynamics. Researchers anticipate that these continued efforts will not only improve the accuracy of predictions concerning these specific particles, but also illuminate broader principles governing the strong force – the fundamental interaction responsible for binding quarks into protons, neutrons, and ultimately, all visible matter – potentially uncovering novel phenomena and challenging existing paradigms within the Standard Model.
The pursuit of understanding the internal structures of hyperons, as demonstrated in this study of the Λ(1405) and Λ(1520), reveals a profound interconnectedness. Analyzing production mechanisms through pion-proton collisions necessitates a holistic view, recognizing that altering one aspect of the system – the collision energy, for example – impacts the entire observable outcome. This resonates with a core principle of elegant design: structure dictates behavior. As Friedrich Nietzsche observed, “There are no facts, only interpretations.” The effective Lagrangian approach employed here isn’t about discovering immutable truths, but rather constructing a coherent framework for interpreting the observed data, acknowledging the inherent subjectivity in defining and understanding complex hadronic systems.
Beyond the Resonance
The pursuit of hadron spectroscopy, as exemplified by this work on Λ(1405) and Λ(1520), frequently resembles an exercise in controlled approximation. The effective Lagrangian, while a powerful tool, inherently trades precision for tractability. It simplifies, necessarily, and these simplifications accumulate. The true cost isn’t necessarily the parameters fitted, but the unmodeled dynamics discarded along the way. Constituent counting rules and Regge trajectories offer compelling frameworks, but they remain, at their heart, phenomenological. The underlying structure, the detailed choreography of quarks and gluons, remains frustratingly obscured by the very methods used to probe it.
Future progress will likely depend not on refining existing techniques, but on embracing a more holistic view. A complete understanding necessitates a synthesis of effective field theories with first-principles calculations, ideally lattice QCD. The challenge lies in bridging the gap between theoretical elegance and experimental accessibility. The Dalitz process, while informative, provides only a snapshot. A dynamic picture-how these resonances evolve within the broader landscape of hadron interactions-is crucial.
Ultimately, the question isn’t simply what these resonances are, but how they fit into the larger architecture of the strong force. The elegance of a physical theory, it is often said, resides in its ability to explain much with little. The current situation suggests a surfeit of parameters and a deficit of fundamental understanding. The next step is not merely to map the resonances, but to discern the principles that govern their existence.
Original article: https://arxiv.org/pdf/2602.11480.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Bitcoin’s Mysterious Millionaire Overtakes Bill Gates: A Tale of Digital Riches 🤑💰
- Gwen Stefani Details “Blessing” of Her Holidays With Blake Shelton
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Wizards of the Coast Unveil New Dungeons & Dragons Game Warlock
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- The $35 Million Crypto Crime: Ex-CFO’s Greed Backfires Spectacularly
- Arnold Schwarzenegger’s Son Patrick Details Growing Up on Movie Sets
- How to Froggy Grind in Tony Hawk Pro Skater 3+4 | Foundry Pro Goals Guide
- How to Get to Heaven from Belfast soundtrack: All songs featured
2026-02-15 22:06