Unlocking the Secrets of Quantum Spin Liquids with Magnetic Fields

Author: Denis Avetisyan

New research explores how applying magnetic fields can reveal exotic phases and emergent behavior in Kitaev spin liquids, pushing the boundaries of condensed matter physics.

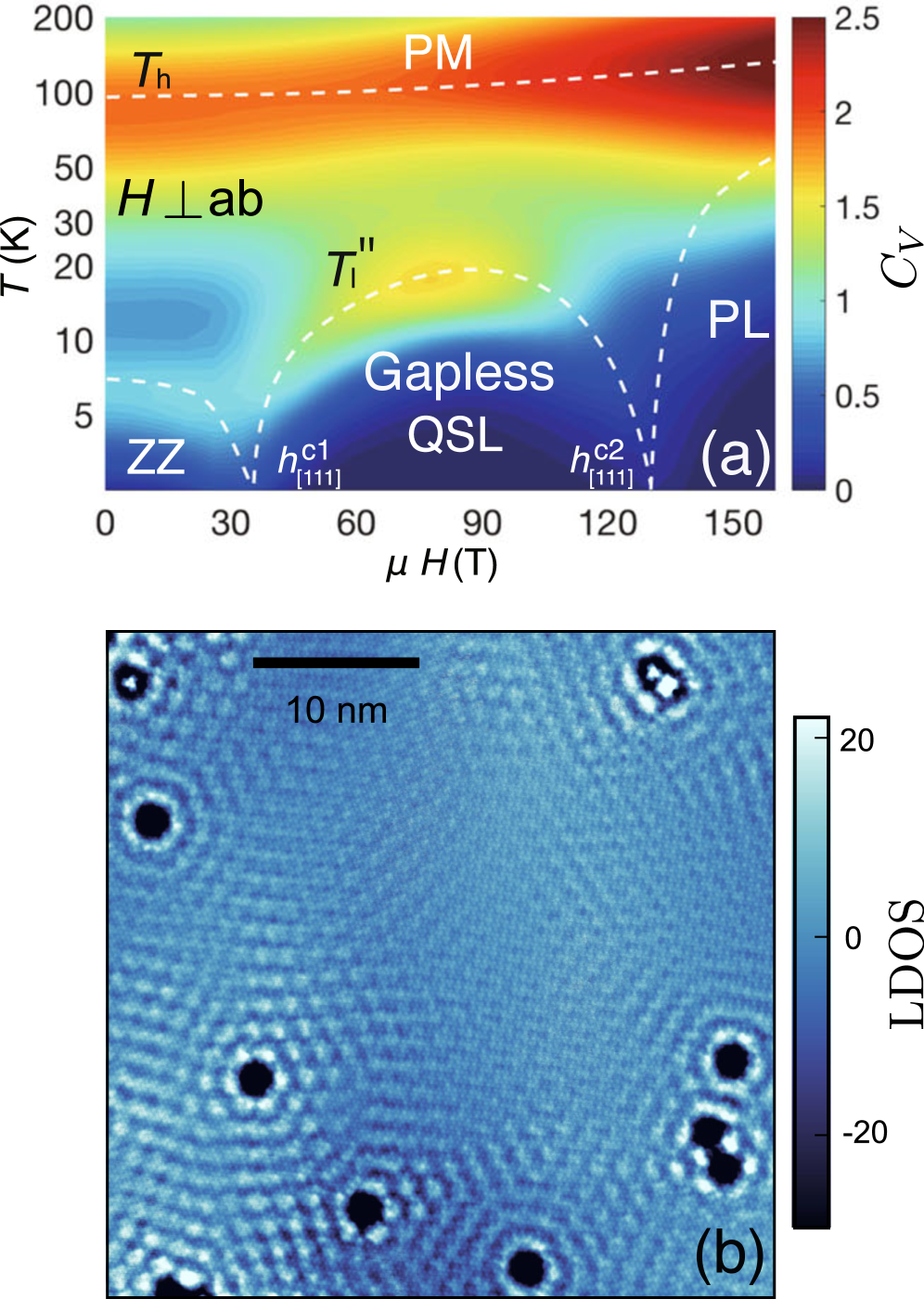
The extended ferromagnetic Kitaev model exhibits a temperature-dependent specific heat influenced by applied magnetic fields, with phase boundaries discernible through simulation, while in monolayer <span class="katex-eq" data-katex-display="false"> \alpha-\alpha-RuCl_3 </span>, the spatial decay of local density of states suggests the presence of gapless Majorana fermions manifesting as spinon Friedel oscillations. — The extended ferromagnetic Kitaev model exhibits a temperature-dependent specific heat influenced by applied magnetic fields, with phase boundaries discernible through simulation, while in monolayer $\alpha-\alpha-RuCl_3$ , the spatial decay of local density of states suggests the presence of gapless Majorana fermions manifesting as spinon Friedel oscillations.

This review details recent advances in understanding field-induced phase transitions, Majorana fermion dynamics, and fractionalization phenomena within the Kitaev honeycomb model.

Identifying and characterizing fractionalized excitations remains a central challenge in understanding quantum spin liquids, despite their theoretical promise. This review, ‘Magnetic field induced phenomena in Kitaev spin liquids’, surveys recent theoretical and numerical advances concerning magnetic field-induced phases within the Kitaev honeycomb model, focusing on emergent phenomena like the quantum Majorana metal and sub-dimensional dynamics. We highlight how applied fields can both stabilize these exotic states and complicate the isolation of specific fractionalized quasiparticles, such as Majorana fermions and $Z_2$ fluxes. Ultimately, can we leverage experimental probes-including neutron scattering, resonant inelastic X-ray scattering, and pump-probe spectroscopy-to definitively identify and characterize these field-induced spin-liquid phases and their unusual fractionalized excitations?

Beyond Conventional Magnetism: The Allure of the Kitaev Model

Traditional investigations into quantum magnetism frequently employ approximations and simplifications to render complex systems tractable. While these approaches have yielded valuable insights, they often fall short when attempting to describe the more elusive and unconventional phases of matter. Many materials exhibit behaviors that defy explanation through conventional magnetic models, hinting at underlying physics beyond their scope. These limitations stem from the inherent difficulty in accurately representing the intricate interplay of quantum interactions within real materials, particularly those with strong correlations between electron spins. Consequently, researchers have sought novel theoretical frameworks capable of capturing these exotic phases, recognizing that a departure from established methods is crucial to unlocking a deeper understanding of quantum magnetism and its potential applications.

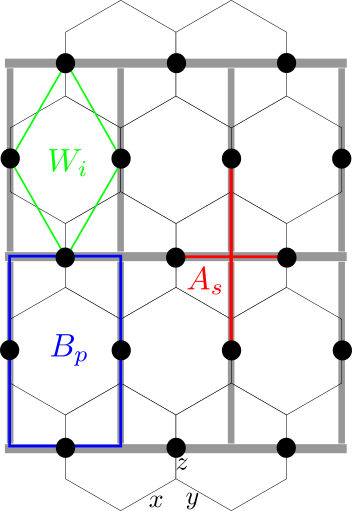
The Kitaev honeycomb model represents a significant departure from conventional approaches to understanding quantum magnetism, offering a rare, exactly solvable framework for exploring the elusive quantum spin liquid phase. Unlike traditional models reliant on approximations, this model utilizes a specific arrangement of spins on a honeycomb lattice and introduces bond-dependent interactions – meaning the strength of interaction varies depending on the link between spins. This seemingly simple alteration has profound consequences, allowing physicists to analytically determine the system’s behavior and predict the emergence of fractionalized excitations – quasiparticles with properties unlike those found in conventional materials. The model’s solvability isn’t merely a mathematical curiosity; it provides a crucial testing ground for theories of quantum spin liquids and a roadmap for identifying potential materials exhibiting this exotic state of matter, potentially paving the way for advancements in quantum computing and materials science.

The Kitaev model distinguishes itself from conventional magnetic systems through interactions that aren’t simply determined by the distance between spins, but rather by the specific bond connecting them. This bond-dependent approach – where interactions vary depending on the direction of the connection within the honeycomb lattice – allows for a fundamentally different type of magnetic frustration. Unlike traditional magnets that tend towards ordered states, this frustration in the Kitaev model prevents conventional magnetic order, instead fostering a highly entangled quantum state known as a quantum spin liquid. Within this exotic phase, spins remain disordered even at absolute zero, and the system exhibits fractionalized excitations – quasiparticles with properties unlike anything seen in conventional magnetism. These emergent phenomena, including Majorana fermions, hold potential for applications in fault-tolerant quantum computing, making the Kitaev model a focal point for condensed matter physics research and a pathway to understanding entirely new states of matter.

Weak magnetic fields applied to Kitaev’s Abelian quantum spin liquid (or toric code) reveal constrained quasiparticle dynamics-a single particle remains immobile while composites move in one dimension-and demonstrate that this anisotropic honeycomb model is equivalent to a family of models related by duality transformations and unitary rotations.

Fractionalized Excitations: Beyond Simple Spin Oscillations

Conventional magnetic materials exhibit excitations that are collective oscillations of electron spins. In contrast, the Kitaev model predicts fractionalized excitations – quasiparticles that do not exist as independent entities in the underlying electron system. Specifically, the model features Z2 flux, representing a topological constraint on spin configurations, and Majorana fermions, which are emergent particles with unique properties. These excitations arise from the model’s specific bond-dependent interactions and are not simply perturbations of the original electron spins; rather, they represent fundamentally new degrees of freedom within the system. The existence of these fractionalized excitations is a key characteristic distinguishing the Kitaev model from traditional magnetic systems.

Unlike conventional quasiparticles arising from electron interactions, Z2 flux and Majorana fermions in the Kitaev model are emergent excitations, meaning they are not directly attributable to simple modifications of electron spin states. These particles possess non-trivial exchange statistics; exchanging two identical Majorana fermions does not result in a sign change of the wavefunction, unlike bosons or fermions. Specifically, Majorana fermions are their own antiparticles, leading to a $\sqrt{2}$ -fold degeneracy in the ground state when confined, and their exchange operation results in a $2\pi$ phase shift rather than the typical π or 0 shift. This fundamentally different behavior arises from the model’s specific spin interactions and the resulting fractionalization of electron degrees of freedom.

Majorana fermions are unique quasiparticles distinguished by being their own antiparticle, meaning a particle and its antiparticle share the same properties. This characteristic arises from a specific symmetry in their creation and annihilation operators, described mathematically as $\gamma = \gamma^{\dagger}$ . The existence of these particles is strongly indicative of topological order, a phase of matter characterized not by broken symmetry, but by non-local correlations and robust boundary states. Unlike conventional particles, Majorana fermions do not have a well-defined quantum number associated with particle number conservation, and their presence fundamentally alters the system’s excitation spectrum and statistical properties, providing a key signature for identifying topologically ordered phases.

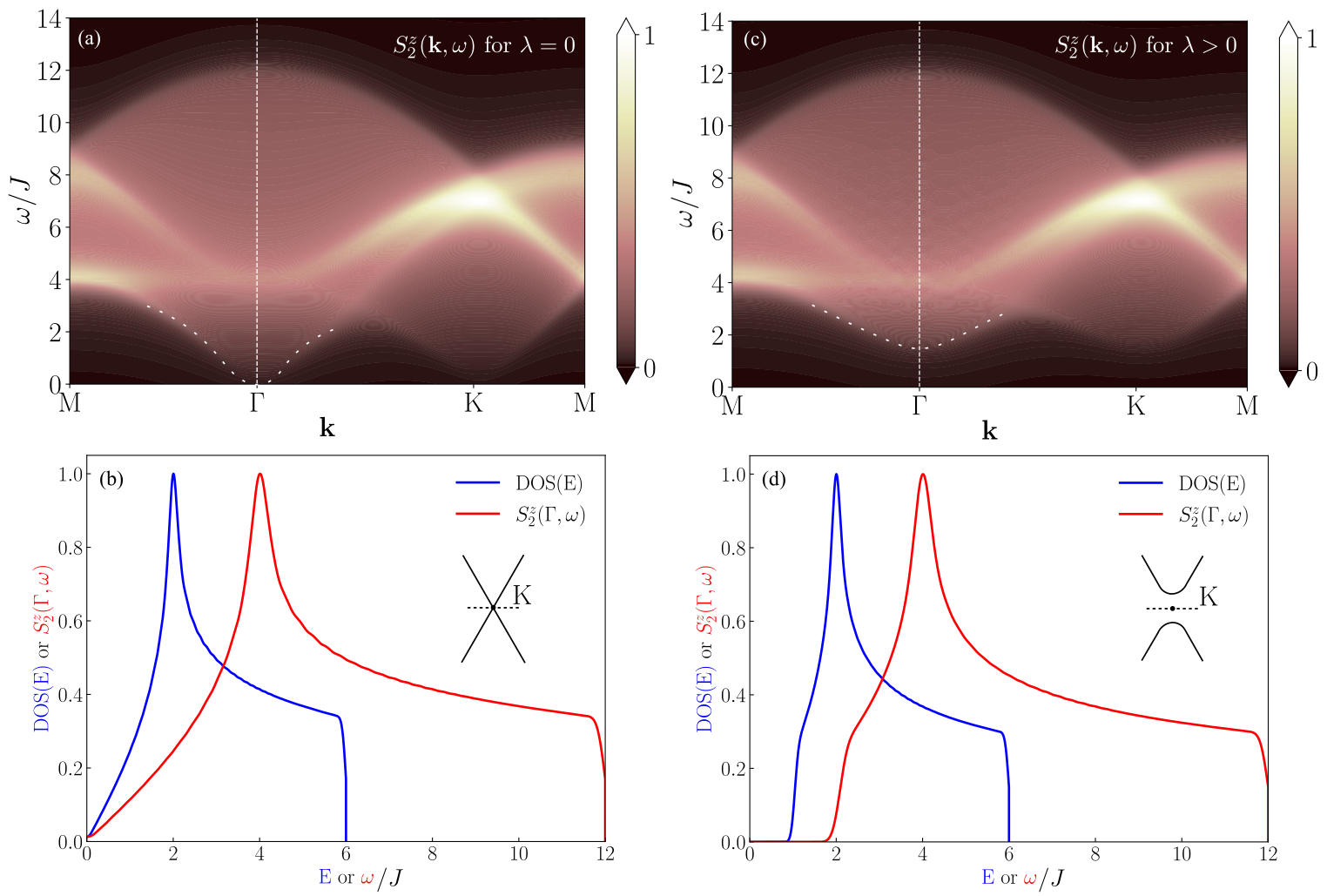
The dynamical spin structure factor <span class="katex-eq" data-katex-display="false">S_2(\mathbf{k},\omega)</span> of the isotropic Kitaev model reveals a gapless spectrum at the Γ point in the time-reversal symmetric phase (<span class="katex-eq" data-katex-display="false">\lambda = 0</span>), which transforms into a gapped spectrum with broken time-reversal symmetry (<span class="katex-eq" data-katex-display="false">\lambda > 0</span>), demonstrating a direct correspondence between the Majorana fermion density of states and the dimer spectral function up to an energy scaling factor. — The dynamical spin structure factor $S_2(\mathbf{k},\omega)$ of the isotropic Kitaev model reveals a gapless spectrum at the Γ point in the time-reversal symmetric phase ( $\lambda = 0$ ), which transforms into a gapped spectrum with broken time-reversal symmetry ( $\lambda > 0$ ), demonstrating a direct correspondence between the Majorana fermion density of states and the dimer spectral function up to an energy scaling factor.

Mapping the Quantum Spin Liquid: Computational Approaches

Characterizing quantum spin liquid (QSL) states presents significant computational challenges due to the strong correlations inherent in these systems. Traditional methods struggle with the exponential growth of the Hilbert space as the number of interacting spins increases. This necessitates the application of advanced numerical techniques, such as the density matrix renormalization group (DMRG) and infinite projected entangled pair states (iPEPS), which efficiently represent the many-body wavefunction by focusing on the most relevant degrees of freedom and truncating less important configurations. These methods allow researchers to approximate the ground state properties and excitation spectra of QSL candidates, providing crucial data for identifying and understanding these exotic phases of matter. The accuracy of these approximations depends heavily on the system size and the specific parameters used in the numerical calculations.

The Density Matrix Renormalization Group (DMRG) is a numerical method particularly well-suited for analyzing the low-energy physics of one-dimensional quantum systems. Its efficacy stems from representing the many-body wave function as a matrix product state (MPS), allowing for a systematic truncation of Hilbert space based on entanglement. This approach enables accurate calculations of ground state energies, correlation functions, and other observables for systems with a large number of sites, exceeding the capabilities of exact diagonalization. While DMRG’s computational cost scales exponentially with the bond dimension used to represent entanglement, it remains a highly efficient technique for one-dimensional systems and serves as a benchmark for other numerical methods.

Infinite Projected Entangled Pair States (iPEPS) represent a tensor network ansatz adapted for simulating two-dimensional quantum many-body systems, overcoming limitations of one-dimensional methods like Density Matrix Renormalization Group (DMRG). Specifically, iPEPS has become a critical tool for investigating the Kitaev model, a paradigmatic example of a quantum spin liquid. Recent calculations utilizing iPEPS have definitively demonstrated the presence of a finite density of states at zero energy within the Kitaev model, a key characteristic predicted for this exotic phase of matter and a strong indicator of its fractionalized excitations and absence of conventional magnetic order. These computations require significant computational resources due to the exponential growth of the parameter space with system size and bond dimension.

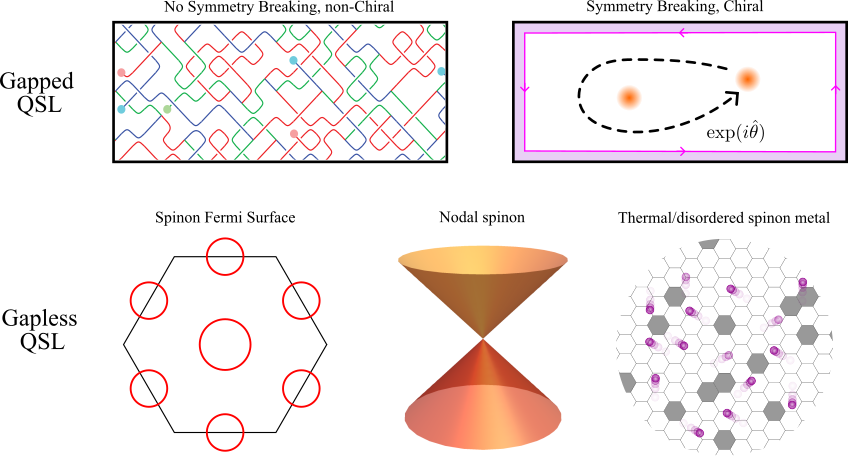
Two-dimensional quantum spin liquids bifurcate into gapped states exhibiting either non-chiral topological order (like string-net states) or chiral order with quantized thermal Hall conductance, or gapless states including spinon Fermi surfaces, Dirac liquids, and disorder-driven metallic phases.

Beyond Idealizations: Real Materials and Dimensional Crossover

The pursuit of novel quantum phases, such as the quantum spin liquid (QSL) predicted for the idealized Kitaev honeycomb lattice, is frequently challenged by the imperfections inherent in real materials. While theoretical models provide a crucial foundation for understanding emergent phenomena, actual compounds deviate from these perfect structures due to factors like bond distortions, off-plane displacements, and the presence of additional magnetic interactions. These deviations can significantly alter the electronic and magnetic properties, suppressing the QSL phase or giving rise to unexpected behaviors. Consequently, researchers must carefully consider the impact of these structural and chemical irregularities when interpreting experimental results and bridging the gap between theoretical predictions and observed phenomena. Understanding how these imperfections influence the material’s behavior is therefore paramount to realizing and manipulating QSL states in practical systems.

The behavior of materials constrained to near-one-dimensional geometries is often governed by a phenomenon known as dimensional crossover. While strictly quasi-one-dimensional, these systems don’t remain isolated; interactions between chains, or layers, introduce effective dimensions that change with external conditions like temperature or magnetic field. This isn’t a simple shift, but rather a complex interplay where the system transitions from behaving as a truly one-dimensional entity to exhibiting characteristics of higher dimensionality. Understanding this crossover is critical because the dimensionality profoundly influences collective behaviors; for example, fluctuations that are suppressed in higher dimensions can dominate in lower dimensions, altering magnetic ordering or promoting exotic quantum phases. Therefore, observing and modeling this dimensional change provides valuable insight into the emergent properties of these materials and allows researchers to predict and control their functionalities.

The existence of a quantum spin liquid (QSL) phase is profoundly sensitive to the delicate balance between dimensionality and magnetic interactions within a material. While idealized models often predict QSL behavior in two dimensions, real materials exhibit complexities that can suppress this phase. Recent studies reveal that applying strong magnetic fields to certain candidate QSL materials induces a transition towards effectively one-dimensional behavior, where individual spin chains decouple from their neighbors. This decoupling, evidenced by emergent low-dimensional characteristics, effectively stabilizes the spin chains against further entanglement and suppresses the QSL phase. The observed transition highlights that the interplay between dimensionality – dynamically altered by external fields – and the strength of inter-chain interactions is crucial for determining the stability and ultimate fate of the QSL state, offering insights into manipulating quantum states of matter.

The anisotropic Kitaev model on a honeycomb lattice can be mapped to an effective square lattice of spin dimers, where the dimer degrees of freedom τ are represented by pairs of σ spins on the bonds, and the resulting effective stabilizers are sensitive to perturbations.

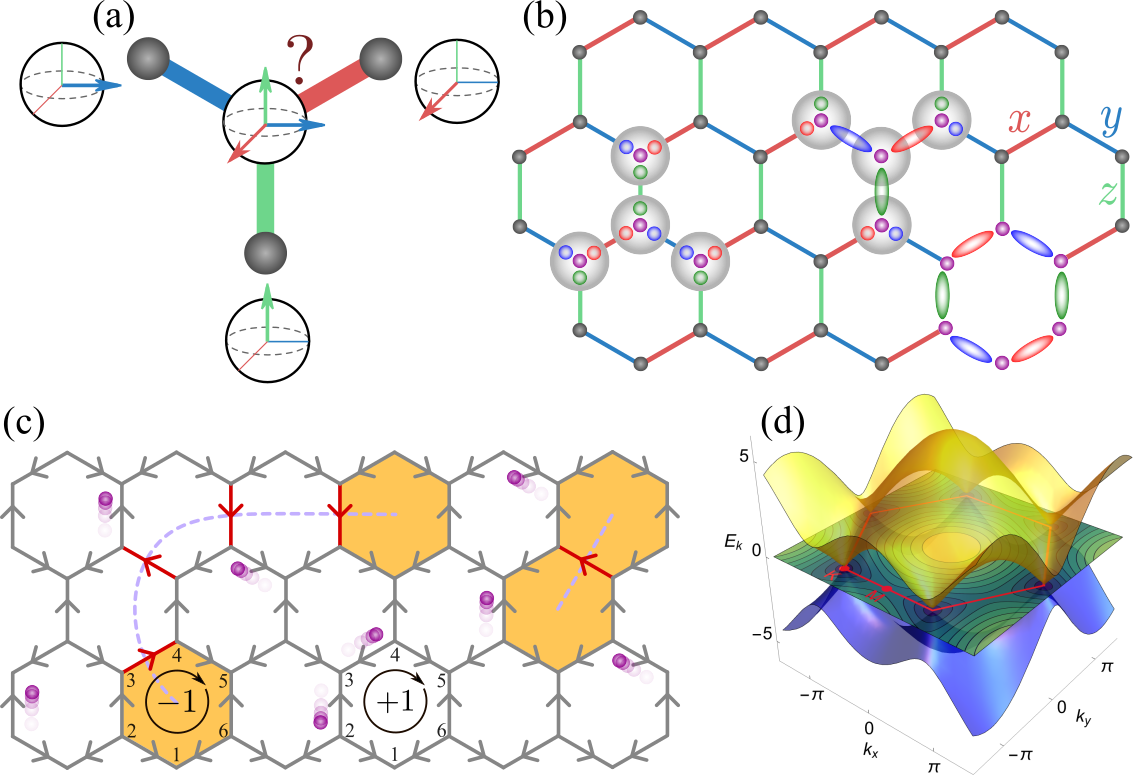
The Promise of Topological Quantum Computation

Quantum computation, while promising revolutionary processing power, is notoriously susceptible to errors arising from environmental noise. A potential solution lies in harnessing the unique properties of non-Abelian anyons, quasiparticles that exhibit exotic exchange statistics. Unlike bosons or fermions, exchanging two identical non-Abelian anyons doesn’t simply change the wavefunction by a phase; instead, it performs a unitary transformation, effectively encoding quantum information in a topologically protected manner. Majorana fermions, a specific type of non-Abelian anyon, are particularly attractive because their defining characteristic – being their own antiparticle – leads to robust quantum states resilient to local disturbances. This topological protection means that quantum computations performed using these anyons are inherently less prone to errors, offering a pathway toward building fault-tolerant quantum computers – machines capable of reliably solving problems currently intractable for even the most powerful classical computers. The potential to braid these anyons, manipulating their positions to perform logical operations, is central to this approach, promising a future where quantum information remains secure even in noisy environments.

Determining the existence and properties of topological order relies heavily on specific experimental probes. Researchers are actively pursuing measurements of the spin structure factor, which reveals the correlated magnetic excitations within a material and can distinctly identify the signatures of topological phases. Simultaneously, probing chiral edge states – conducting pathways existing at the boundaries of a topological material – offers direct evidence of protected, unidirectional electron flow. These edge states are remarkably robust against disorder and imperfections, a hallmark of topological protection, and their observation provides compelling evidence for non-trivial topological order. Combined, these techniques represent crucial steps towards not only confirming the presence of topological phases but also mapping out their intricate properties and ultimately harnessing them for technological applications.

The pursuit of robust quantum computation increasingly focuses on material innovation, driven by the potential of topological quantum devices. Researchers are actively exploring and engineering novel quantum materials exhibiting characteristics conducive to hosting exotic states of matter, such as Majorana fermions. Recent breakthroughs have identified materials displaying a ‘flux gap’ of zero, a key signature consistent with the formation of a Majorana metal – a state where these unique, potentially fault-tolerant, particles emerge. This discovery suggests a viable pathway toward creating stable qubits, protected from environmental noise, and represents a crucial step in translating the theoretical promise of topological quantum computation into tangible technological advancements. The ongoing materials science efforts aim to refine these systems and unlock the full potential of topologically protected quantum information processing.

Spin-orbital frustration in a honeycomb lattice fractionalizes local spins into Majorana fermions, creating a <span class="katex-eq" data-katex-display="false">Z_2</span> gauge field and allowing for the propagation of itinerant fermions that form Dirac cones, with excitations induced by flipping bonds around hexagonal plaquettes. — Spin-orbital frustration in a honeycomb lattice fractionalizes local spins into Majorana fermions, creating a $Z_2$ gauge field and allowing for the propagation of itinerant fermions that form Dirac cones, with excitations induced by flipping bonds around hexagonal plaquettes.

The pursuit of topological order, as detailed in this exploration of the Kitaev model, feels predictably ambitious. It’s a beautiful construction, this attempt to corral Majorana fermions and observe field-induced phase transitions, but one suspects production-or, in this case, experimental verification-will inevitably introduce complications. As David Hume observed, “The mind is willing to receive any false impression, rather than admit its ignorance.” This paper meticulously builds an elegant theoretical framework, outlining the emergence of a quantum Majorana metal, but the path from theory to demonstrable reality is rarely smooth. The dimensional crossover described here is likely to present unforeseen challenges, a reminder that every abstraction dies in production, even if it dies beautifully.

What’s Next?

The pursuit of emergent phenomena in the Kitaev model, particularly under external fields, reveals a familiar pattern. Each refined theoretical construct, each numerically stabilized phase, merely defines the next order of instability. The Majorana metal, so elegantly predicted, will undoubtedly exhibit behaviors production – in the form of real materials and imperfect conditions – finds a way to elicit. The dimensional crossover, currently a topic of intense scrutiny, will likely yield not to simple scaling, but to the complex interplay of anisotropies and disorder inherent in any physical system.

The challenge isn’t to find the perfect Kitaev material, but to understand how deviations from the ideal model manifest. The field-induced phases are not destinations, but transient states en route to thermodynamic equilibrium-or, more likely, to a new form of frustration. Every optimization will one day be optimized back. The emphasis will shift from seeking topological order as a static property, to characterizing its dynamics and resilience against perturbations.

It’s reasonable to anticipate that the most significant advances will not come from increasingly sophisticated theoretical models, but from the development of experimental probes capable of resolving the subtle signatures of fractionalization and sub-dimensional behavior. The architecture isn’t a diagram; it’s a compromise that survived deployment. The true test will be whether these theoretical constructs can withstand the unforgiving scrutiny of the laboratory-or, if they, too, become merely footnotes in the ever-expanding history of condensed matter physics.

Original article: https://arxiv.org/pdf/2601.14496.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/