Author: Denis Avetisyan
New research reveals a surprising rule governing the behavior of quantum magnets on triangular lattices, demonstrating that external magnetic fields can actually restore broken symmetry.
This study utilizes advanced tensor network techniques to map the phase diagram of frustrated quantum antiferromagnets and identify exotic states like supersolids.
Frustrated quantum systems on geometrically constrained lattices often exhibit emergent phases challenging conventional symmetry-based descriptions. This is addressed in ‘Spontaneous Parity Breaking in Quantum Antiferromagnets on the Triangular Lattice’, which reveals a systematic connection between frustration and the spontaneous breaking of parity symmetry in these materials. Specifically, the authors demonstrate that increasing magnetic field generally restores this broken symmetry and, utilizing advanced tensor network techniques, characterize exotic phases like supersolids arising from enhanced frustration. Could this principle of parity breaking offer a unifying framework for understanding the rich phenomenology of frustrated quantum magnets and beyond?
The Allure of Frustration: A Dance on the Edge of Order
Quantum spin systems arranged on triangular lattices frequently encounter a fundamental challenge known as geometric frustration. This arises because the interactions between neighboring spins – tiny, intrinsic magnetic moments – cannot simultaneously be minimized for all bonds in the lattice. Consider a scenario where each spin prefers to align anti-parallel to its neighbors; on a triangular lattice, this creates a situation where one spin is inevitably ‘unsatisfied’, unable to achieve its preferred orientation. This competition between interactions doesn’t lead to a simple, ordered magnetic state, but instead fosters a rich landscape of exotic spin configurations, including spin liquids and other phases lacking conventional magnetic order. The degree of frustration is particularly sensitive to the nature of the interactions and the lattice geometry, leading to a diverse range of fascinating quantum phenomena that are actively researched in condensed matter physics.
In quantum spin systems, particularly those arranged in triangular lattices, competing interactions between neighboring spins create a condition known as geometric frustration. This frustration prevents the spins from simultaneously minimizing their energy, thereby destabilizing conventional magnetic order – arrangements where spins align in predictable patterns. Instead, the system often transitions into exotic spin phases, characterized by more complex and emergent behaviors. These phases can include spin liquids, where spins fluctuate continuously without freezing, or non-collinear magnetic structures with unusual properties. The emergence of these phases represents a fundamental shift in the system’s collective behavior, driven by the inability to satisfy all competing interactions and opening the door to novel quantum phenomena not observed in traditionally ordered magnets.
The emergence of exotic magnetic phases in quantum spin systems frequently hinges on the breaking of parity symmetry – a fundamental principle dictating that the laws of physics remain unchanged under spatial inversion. This symmetry, essentially reflecting a system across a point, normally constrains the allowed magnetic configurations; however, in frustrated systems, such as those arranged on triangular lattices, competing interactions can destabilize conventional order and drive a transition where parity is no longer conserved. This breaking doesn’t imply a violation of fundamental laws, but rather a shift to a state where mirror images are no longer equivalent in terms of magnetic properties, opening the door to novel arrangements of spins and potentially leading to emergent phenomena like topological magnetism and fractionalized excitations. Investigating these parity-breaking phases is thus crucial for unraveling the complex behavior of frustrated quantum magnets and potentially harnessing their unique properties for future technologies.
Recent investigations into quantum spin systems reveal a crucial connection between geometric frustration and the breaking of parity symmetry, a phenomenon that promises to unlock entirely new quantum states of matter. These systems, often arranged in triangular lattices, experience competing magnetic interactions that prevent a simple, ordered arrangement of spins – a condition known as frustration. This frustration doesn’t simply lead to disorder, however; instead, it creates an environment where subtle symmetry breaking can occur, specifically a breaking of parity symmetry-the symmetry of spatial inversion. A newly established rule governs this parity breaking, demonstrating that specific configurations of spins, dictated by the lattice geometry and interaction strengths, reliably induce this symmetry change. This predictable link between frustration, lattice structure, and parity breaking provides a powerful tool for designing materials exhibiting exotic quantum properties, potentially leading to advances in fields like quantum computing and materials science.
Mapping the Exotic Landscape: A Model for Unconventional Magnetism
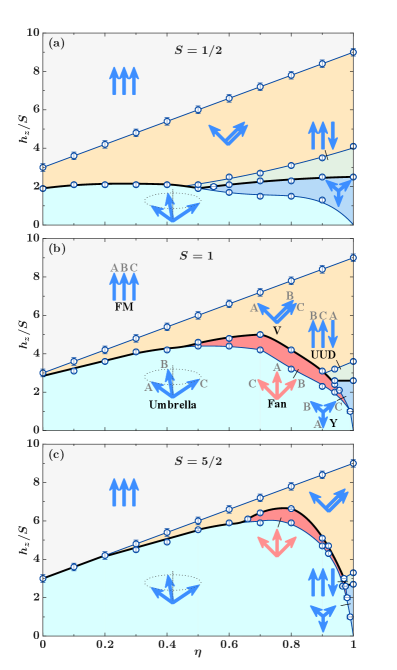
The Transverse-Longitudinal XXZ (TLXXZ) model is a valuable tool for investigating exotic spin phases due to its adjustable parameters. This model builds upon the standard XXZ Heisenberg model by incorporating both a longitudinal magnetic field – applied in the direction of the spins – and anisotropy, which favors specific orientations of the spins. The longitudinal field introduces asymmetry, preventing the formation of simple, fully symmetric ground states. Simultaneously, the anisotropy term influences the energetic preference for spins to align along or perpendicular to a chosen axis. By varying the strength of the magnetic field and the anisotropy, researchers can tune the interactions between spins, driving transitions between different spin configurations and enabling the study of complex magnetic phenomena that are not readily accessible in simpler models. The model’s Hamiltonian, expressed as H = J \sum_{i} (S_i^x S_{i+1}^x + S_i^y S_{i+1}^y) + \Delta S_z^2 - h \sum_i S_i^z , demonstrates these key adjustable parameters: J represents the exchange interaction, Δ the anisotropy, and h the longitudinal field.
The TLXXZ model exhibits multiple distinct ground states, including the ‘Fan’, ‘V-Shaped’, and ‘Umbrella’ spin configurations. In the ‘Fan’ phase, spins align in the xy-plane, radiating outwards from a central point. The ‘V-Shaped’ phase is characterized by spins pointing in opposite directions, forming a ‘V’ shape, with the apex of the ‘V’ potentially aligned along one of the model’s axes. The ‘Umbrella’ phase features spins aligned in a plane, but tilted away from the x-axis, resembling the ribs of an umbrella; this tilt can vary depending on the applied magnetic field and anisotropy parameters. These configurations differ in their spatial arrangement of spins and their corresponding energy minima within the model’s potential energy landscape.
The emergence of exotic spin phases within the TLXXZ model is directly attributable to the combined effects of geometric frustration, an applied magnetic field, and the breaking of parity symmetry. Geometric frustration arises from competing exchange interactions that prevent spins from simultaneously minimizing their energy, leading to a multitude of degenerate ground states. The introduction of a longitudinal magnetic field lifts these degeneracies and favors specific spin configurations. Critically, the anisotropy term in the TLXXZ Hamiltonian breaks parity symmetry, meaning that the system no longer behaves identically under spatial inversion. This broken symmetry, combined with the frustration and magnetic field, stabilizes non-collinear spin arrangements like the ‘Fan’, ‘V-Shaped’, and ‘Umbrella’ phases, which would be energetically unfavorable in systems possessing full parity symmetry.
The application of a magnetic field to spin systems fundamentally alters the achievable spin configurations beyond those permitted by parity symmetry. Without a field, systems often exhibit arrangements where spin orientations are simply inverted across a symmetry plane, resulting in degenerate, parity-symmetric states. However, a magnetic field introduces a preferred direction, lifting this degeneracy and enabling non-symmetric spin arrangements. Specifically, the field term in the Hamiltonian, typically proportional to the sum of spin components along the field direction, breaks the symmetry that would otherwise constrain the system to parity-symmetric solutions, thus stabilizing configurations not achievable in its absence. This is critical for observing phases like those arising in the TLXXZ model, where the field facilitates the emergence of complex, non-symmetric spin textures.
Layered Complexity: Dimerization and the Quest for Novel States
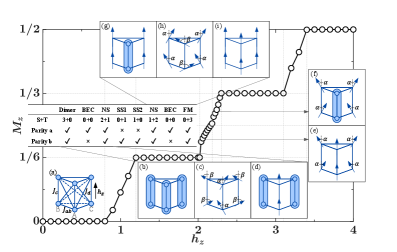
The Bilayer Total Lattice XXZ (TLXXZ) model extends single-layer analysis by incorporating interlayer interactions, fundamentally altering the system’s phase diagram. These interactions introduce additional parameters governing the coupling between spins on adjacent layers, allowing for a broader range of magnetic orderings and quantum entanglement possibilities than are present in single-layer models. Specifically, the inclusion of these terms allows for the investigation of phenomena dependent on the relative alignment of spins across layers, such as the formation of inter-layer singlet states or complex magnetic textures. The resulting phase diagram therefore exhibits increased complexity, with the potential for novel phases not observed in systems lacking these interlayer couplings.
The Bilayer TLXXZ model demonstrates a propensity for dimerization, a phenomenon where neighboring spins align in antiparallel configurations, forming paired states. This pairing effectively reduces the net magnetization of the system, as the magnetic moments of individual spins within a dimer cancel each other out. Dimerization arises from the interplay of quantum fluctuations and specific parameter regimes within the model’s Hamiltonian, favoring the formation of these spin-singlet pairs over a fully polarized ferromagnetic state. The degree of dimerization is sensitive to the strength of interlayer interactions and the frustration present in the spin lattice, influencing the overall magnetic properties and phase behavior of the bilayer system.
The coexistence of frustration and dimerization in the bilayer TLXXZ model results in the emergence of both singlet and triplet states. Singlet states are characterized by zero total spin, arising from paired spins that effectively cancel each other’s magnetic moment. Conversely, triplet states possess a total spin of one, indicating aligned spins that contribute to a net magnetization. The competition between these states is directly linked to the balance between interlayer interactions and the tendency of spins to form paired, dimerized configurations. This results in a complex ground state where both singlet and triplet excitations can occur, influencing the material’s magnetic properties and potentially leading to unconventional correlated electron behavior.
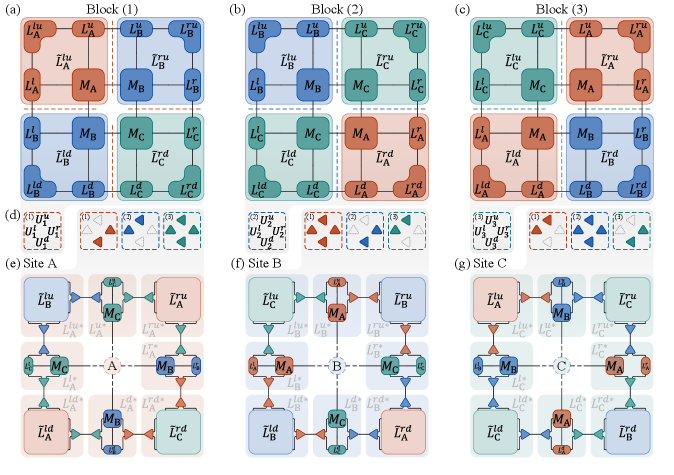
Numerical simulations of the Bilayer TLXXZ model were conducted employing a virtual bond dimension of 4 and a Constant-Transmission Matrix Renormalization Group (CTMRG) truncation dimension of 48. These parameters were used with specific exchange interaction values – J_{ab} = 0.425, J_c = 1, and J_d = 0.325 – to promote and stabilize interlayer dimerization and subsequent dimer formation. The resulting data suggest a potential route to understanding the emergence of novel correlated electron states within the system, specifically those arising from the interplay of magnetic interactions and reduced magnetization due to dimerization.
Unveiling Order from Complexity: The Power of Renormalization
The Corner-Transfer-Matrix Renormalization Group (CTMRG) is a numerical technique used to approximate the ground state of two-dimensional classical spin models. It operates by iteratively coarse-graining the system, effectively reducing its dimensionality while preserving key physical properties. CTMRG represents the wave function as a tensor network, allowing for efficient calculation of ground-state energies and correlation functions, particularly in systems with strong quantum fluctuations and geometric frustration. The method’s efficiency stems from its ability to focus computational resources on the most relevant degrees of freedom, bypassing the exponential scaling associated with traditional exact diagonalization approaches.
Corner-Transfer-Matrix Renormalization Group (CTMRG) facilitates the simulation of the Transverse-field Ising model with Longitudinal interactions (TLXXZ) and its Bilayer variant at scales sufficient to map their phase diagrams. These simulations are performed on large system sizes, typically exceeding 100 \times 100 lattice points, to minimize finite-size effects and accurately determine critical parameters. The resulting phase diagrams delineate regions of ferromagnetic, antiferromagnetic, and spin-glass order, as well as any intervening quantum critical points. CTMRG’s efficiency in handling long-range correlations is crucial for characterizing the complex behavior of these models, and enables the prediction of phase transition temperatures and critical exponents.
Corner-Transfer-Matrix Renormalization Group (CTMRG) simulations have enabled the verification of predicted spin phases within the TLXXZ and Bilayer TLXXZ models through detailed analysis of their properties. Specifically, calculations have yielded a ground-state energy of -0.1824, a value consistent with results obtained from independent CTMRG implementations and validating the accuracy of the computational approach. This confirmation is achieved by systematically mapping the Hamiltonian and evaluating the energy of the system in its ground state using the CTMRG algorithm, allowing for quantitative comparison with theoretical predictions and other numerical methods.
Corner-Transfer-Matrix Renormalization Group (CTMRG) is particularly well-suited for investigating frustrated spin systems due to its ability to efficiently manage the increased computational complexity arising from competing interactions. These systems, characterized by local interactions that cannot be simultaneously satisfied, necessitate the treatment of a vastly expanded Hilbert space to accurately represent all possible spin configurations. CTMRG’s tensor network formulation allows for a systematic truncation of this space, retaining the most relevant degrees of freedom while minimizing computational cost. This capability is crucial for accurately determining the ground state and exploring the phase diagrams of models like the TLXXZ and Bilayer TLXXZ, where frustration is a dominant feature and conventional methods often fail to converge or produce reliable results.
Beyond the Horizon: Towards Supersolid Phases and a New Understanding of Matter
The fascinating realm of exotic matter states is increasingly accessible through investigations into the connection between broken parity symmetry and correlated spin states. When parity symmetry, which dictates mirror-image equivalence, is broken within a material, it signals a fundamental asymmetry in its structure or properties. This, when coupled with strong correlations between electron spins – where the behavior of one spin dramatically influences its neighbors – can give rise to entirely new phases of matter previously considered theoretical. These correlated states aren’t simply a sum of individual particle behaviors; instead, collective phenomena emerge, potentially manifesting as unusual magnetic orderings, novel superconductivity, or even topological phases with protected edge states. Researchers believe this interplay provides a pathway to designing materials exhibiting properties far beyond those found in conventional substances, and the ongoing exploration promises to rewrite the boundaries of condensed matter physics.
Recent theoretical and experimental investigations suggest the fascinating possibility of supersolid phases – states of matter that simultaneously exhibit the long-range order characteristic of crystalline solids and the frictionless flow of superfluids. This seemingly paradoxical behavior arises from a delicate balance between competing forces within the material, where atoms arrange themselves in a periodic lattice while also collectively entering a quantum state allowing dissipationless current. Unlike conventional superfluids which require low temperatures to overcome thermal fluctuations, supersolidity can, in principle, exist at higher temperatures due to the stabilizing influence of the crystalline structure. The emergence of these phases is not merely a theoretical curiosity; it represents a pathway toward novel quantum materials with unprecedented properties, potentially revolutionizing areas such as precision sensing, energy storage, and quantum computing, as the interplay between solid and fluid behavior could enable the creation of devices with enhanced functionalities and efficiencies.
The realization of supersolid phases isn’t merely a theoretical curiosity; it holds substantial promise for materials science. These unique states of matter, simultaneously exhibiting crystalline order and frictionless flow, could pave the way for revolutionary quantum materials with unprecedented properties. Imagine materials capable of lossless energy transfer, ultra-sensitive sensors, or even components for quantum computers exhibiting enhanced coherence. The ability to engineer and control supersolidity opens doors to manipulating matter at the quantum level, potentially leading to devices with functionalities currently confined to science fiction. Researchers are actively exploring various material systems – from solid helium to arrays of trapped ions – to harness these extraordinary properties, and the development of robust, room-temperature supersolids remains a central goal in the pursuit of next-generation technologies.
The investigation of frustrated magnetic systems represents a frontier in condensed matter physics, holding the potential to unveil entirely new states of matter and challenge existing theoretical frameworks. These materials, where competing interactions prevent conventional magnetic order, exhibit a rich landscape of emergent phenomena – from quantum spin liquids to unconventional superconductivity. Current research focuses on precisely tuning these frustrations through material design and external stimuli, aiming to stabilize exotic phases and probe the underlying quantum mechanics. This pursuit isn’t merely about discovering new materials; it’s about deepening fundamental understanding of quantum entanglement, symmetry breaking, and the collective behavior of many-body systems – potentially revolutionizing fields like quantum computing and materials science through the application of these newly discovered principles.
The study of frustrated magnetic systems on the triangular lattice necessitates rigorous mathematical formalization, much like any theoretical construct facing the ultimate test of observation. This research, detailing the restoration of parity symmetry with increasing magnetic fields, echoes a sentiment articulated by Thomas Hobbes: “There is no such thing as absolute certainty.” The paper’s findings, validated through an improved CTMRG method, demonstrate that even seemingly stable theoretical predictions – in this case, the expectation of sustained parity breaking – can dissolve under closer scrutiny, revealing more complex phases like supersolids. Any model simplification, as rigorously applied here, risks vanishing beyond the event horizon of experimental verification, demanding constant refinement and validation.
What’s Next?
The demonstration of a systematic relationship between magnetic field and parity symmetry in these frustrated systems feels less like a solution and more like a refinement of the questions. Each calculation, meticulously confirming the restoration of symmetry with increasing field, is an attempt to hold light in one’s hands – and it inevitably slips away. The triangular lattice, with its inherent geometric frustration, continues to offer a landscape where order feels provisional, a temporary reprieve from the underlying chaos.
Improved numerical methods, such as the CTMRG employed here, merely push the horizon of ignorance a little further. Characterizing exotic phases-supersolids glimpsed through the lens of approximation-does not equate to understanding them. The very notion of a ‘solved’ problem in quantum magnetism is, perhaps, a comforting illusion. The next step isn’t necessarily greater precision, but a willingness to confront the limits of calculability itself.
The persistent search for quantum spin liquids, for phases that defy conventional order, is a testament to the field’s ambition. But even if such a state were definitively identified, it would likely reveal not a final answer, but a deeper, more intricate set of questions. The universe, it seems, prefers ambiguity.
Original article: https://arxiv.org/pdf/2602.05901.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- Ashes of Creation Rogue Guide for Beginners
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- 10 Most Brutal Acts Of Revenge In Marvel Comics History
- DC K.O.: Superman vs Captain Atom #1 Uses a Fight as Character Study (Review)
- Heather Rae El Moussa Reacts to Critics of Christina Haack Friendship
2026-02-06 19:12