Author: Denis Avetisyan
New research demonstrates a powerful method for simulating and verifying non-Abelian anyon behavior in complex many-body systems, paving the way for advancements in topological quantum computation.
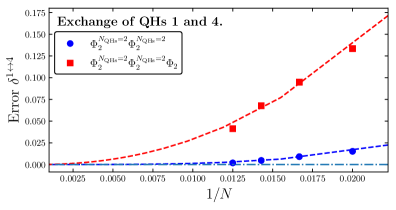
Researchers successfully extract braiding matrices for up to 80 particles, confirming predictions from conformal field theory and the Fibonacci anyon model.
Understanding the emergence of topological order in strongly correlated systems remains a central challenge in condensed matter physics. This is addressed in ‘Non-Abelian fusion and braiding in many-body parton states’, where a framework is developed to construct and analyze quasihole bases for a broad family of non-Abelian fractional quantum Hall states using parton wave functions. The authors demonstrate successful extraction of braiding matrices-even for systems with up to 80 particles-confirming predictions from conformal field theory and level-rank duality, and providing a path toward identifying and characterizing topologically protected quantum information. Could this approach facilitate the design of robust quantum computing architectures based on these exotic states of matter?
The Illusion of Order: Unveiling Fractional Quantum States
The Fractional Quantum Hall Effect (FQHE) demonstrates that electrons, when subjected to intense magnetic fields and cooled to near absolute zero, can coalesce into states of matter exhibiting properties fundamentally different from those predicted by single-particle physics. Rather than behaving as independent entities, electrons become inextricably linked, forming collective excitations that possess fractional charge – values like \frac{e}{3} or \frac{e}{5} – a direct contradiction of the conventional understanding of electrical charge. This isn’t merely a quantitative deviation; it signifies the emergence of entirely new states governed by interactions, where the system’s behavior cannot be explained by simply summing the properties of individual electrons. These exotic states challenge the established framework of condensed matter physics and point to a realm where collective quantum phenomena dominate, offering a glimpse into the complex interplay of many-body interactions and topological order.
The remarkable behavior of electrons in the Fractional Quantum Hall Effect extends beyond simply exhibiting quantized conductance; these systems demonstrate genuinely fractional charge and obey statistics drastically different from those governing everyday particles. Conventional condensed matter physics dictates that charge is quantized in integer multiples of the elementary charge, e, and that particles are either bosons or fermions. However, within the FQHE, quasiparticles emerge with charges like e/3 or e/5, and their exchange operations don’t simply acquire a plus or minus sign – instead, they undergo more complex phase changes indicative of anyonic statistics. This challenges fundamental assumptions about particle identity and necessitates a re-evaluation of the theoretical tools used to describe many-body quantum systems, hinting at emergent phenomena rooted in strong electron correlations and topological order.
Traditional Landau theory, successful in describing the Integer Quantum Hall Effect, falters when applied to the Fractional Quantum Hall Effect due to the strong electron-electron interactions present in these systems. These interactions give rise to correlated many-body states where electrons effectively behave as composite fermions or quasiparticles with fractional charge and statistics – properties fundamentally absent in the single-particle picture of Landau levels. Consequently, physicists have turned to more sophisticated theoretical approaches, including composite fermion theory, hierarchical models, and particularly, powerful numerical techniques like exact diagonalization and density matrix renormalization group, to map out the complex phase diagram of FQHE states. These frameworks attempt to account for the intricate interplay of interactions and correlations, moving beyond the simple harmonic oscillator potential central to Landau theory and offering a path toward understanding the emergent phenomena that define these exotic states of matter.
The pursuit of non-Abelian quantum states within the fractional quantum Hall effect (FQHE) represents a pivotal frontier in the development of topological quantum computation. Unlike conventional qubits susceptible to environmental noise, these exotic states encode quantum information in a fundamentally robust manner, protected by the topology of the electron wavefunction. Specifically, quasiparticles emerging in certain FQHE phases-anyons-obey exchange statistics differing from bosons or fermions, and in non-Abelian scenarios, braiding these anyons alters the quantum state in a way that is resilient to local perturbations. This inherent stability promises fault-tolerant quantum gates, a critical requirement for building scalable quantum computers. Researchers are actively exploring specific FQHE fractions, such as the \nu = 5/2 state, as potential platforms for realizing these topologically protected qubits and manipulating them through precisely controlled experimental conditions, ultimately aiming to harness the unique properties of the FQHE for practical quantum information processing.
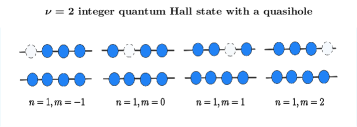
Deconstructing Reality: Partons and Effective Theories
Parton theory proposes a departure from traditional electron-based descriptions of interacting electron systems, positing that the fundamental excitations are not electrons themselves, but rather emergent quasiparticles possessing fractional electric charge. These partons, unlike electrons which carry a charge of -e , exhibit charges that are a fraction of the elementary charge, such as \frac{e}{3} or \frac{e}{5} . This fractionalization arises from strong correlations within the electron system, effectively decoupling the electron’s charge and spin degrees of freedom. The collective behavior of these partons then reconstructs the original electron, though the individual excitations are fundamentally different from the initial constituent particles. This approach is particularly relevant in systems exhibiting exotic quantum phases, where the conventional understanding of electrons breaks down.
Pseudo Landau Levels (PLLs) arise in two-dimensional electron systems subjected to strong magnetic fields and many-body interactions, offering a simplification of the complex many-body problem. Unlike true Landau Levels which are exact solutions to the single-particle Schrödinger equation in a magnetic field, PLLs are approximate levels formed due to the interplay between the kinetic energy of the electrons and the Coulomb interaction. The formation of PLLs effectively reduces the many-body interactions to a single-particle picture, allowing for calculations that are otherwise intractable. The spacing between PLLs is determined by the strength of the Coulomb interaction and the magnetic field, and this modified energy spectrum significantly alters the system’s properties compared to the non-interacting case. Specifically, the density of states is modified, and new collective excitations can emerge due to the altered electronic structure.
Chern-Simons theory offers a compelling description of the low-energy effective field theory governing fractional quantum Hall states and, consequently, parton systems. The theory is characterized by an action S = \in t d^2x \ \epsilon_{\mu\nu} a_\mu J^\nu , where a_\mu is a gauge field and J^\nu is a conserved current associated with the partons. This action naturally incorporates topological terms leading to emergent gauge fields and modifies the statistics of the quasiparticles. Specifically, the theory predicts that the partons can exhibit fractional charge and anyonic statistics – neither bosonic nor fermionic – due to the coupling between the gauge field and the current. The resulting effective field theory simplifies calculations of correlation functions and provides a robust framework for understanding the exotic properties of these strongly correlated electron systems.
The Integer Quantum Hall (IQH) state, characterized by quantized Hall conductance \sigma_{xy} = \nu e^2/h where ν is an integer and e is the elementary charge, serves as a crucial reference point for constructing parton wave functions. Specifically, the Laughlin wave function, \Psi_{L} = \prod_{j<k} (z_j="" -="" [="" [latex]="" \nu="1" a="" allows="" an="" and="" attaching="" be="" by="" can="" composite="" considering="" construction="" correlated="" demonstrating="" describes="" different="" each="" effect.="" electron="" electrons.="" emergence="" established="" even="" exhibits="" exotic="" fermions="" fermions,="" flux="" for="" formed="" fractional="" framework="" functions="" ground="" groundwork="" hall="" interacting="" iqh="" latex]="" latex],="" laying="" like="" magnetic="" mapped="" mapping="" model="" more="" non-interacting="" number="" of="" onto="" order="" p="" parton="" provides="" quanta="" quantum="" quasiparticles="" quasiparticles.<="" representing="" similar="" solvable="" state="" state,="" states="" statistics="" system="" systematic="" systems="" techniques="" the="" this="" to="" topological="" understanding="" utilizing="" wave="" which="" z_k)="" -=""></p> <h2>The Dance of Indistinguishability: Anyons and Braiding</h2> <p>Anyons are quasiparticles that emerge as excitations in two-dimensional systems and exhibit fractional exchange statistics, distinct from the behavior of bosons and fermions. Unlike bosons which have symmetric wavefunctions upon particle exchange, and fermions which have antisymmetric wavefunctions, anyons acquire a phase factor [latex]e^{i\theta} upon exchanging two identical particles, where θ is not restricted to multiples of π. This non-trivial phase results in a wavefunction that is neither fully symmetric nor antisymmetric. The existence of anyons is contingent on the topology of the system and the presence of strong interactions, typically observed in fractional quantum Hall effect systems and certain superconducting materials. Their unique statistical properties are not intrinsic to the particles themselves, but rather arise from the way they move around each other within the confined two-dimensional space.
Unlike bosons or fermions which obey either symmetric or antisymmetric exchange statistics, non-Abelian anyons exhibit statistics where the quantum state of a system changes not just by a phase factor, but by a unitary transformation upon the exchange of two particles. This means the final quantum state depends on the path taken during the exchange - the act of ‘braiding’ anyons alters the wavefunction in a way that is not solely determined by the number of exchanges. Consequently, the order in which anyons are exchanged is significant, and the resulting quantum state is fundamentally different than if the particles were bosons or fermions. This property is a key distinction and enables potential applications in topological quantum computation, where the braiding operations themselves represent quantum gates.
The braiding matrix is a mathematical representation detailing the effect of exchanging two anyons within a system exhibiting non-Abelian statistics. Unlike bosons or fermions where particle exchange results in a phase factor of +1 or -1 respectively, anyon exchange is described by a unitary matrix. This matrix, denoted as B_{ij}, encapsulates the transformation of the many-body quantum state when anyons i and j are exchanged. The elements of the braiding matrix are complex numbers, and crucially, the order of exchange matters; B_{ij} is generally not equal to B_{ji}. This non-commutativity directly reflects the non-Abelian nature of the statistics and is the fundamental property captured by the matrix, allowing for the prediction and analysis of quantum state evolution during braiding operations.
Numerical extraction of braiding matrices, which mathematically represent the exchange statistics of anyons, has been significantly advanced through the application of high-performance computing resources. Specifically, the Nandadevi Supercomputer has facilitated the calculation of these matrices for systems containing up to N=80 quasiparticles. This capability allows for direct comparison between computationally derived braiding matrices and theoretical predictions based on models of non-Abelian anyons, providing empirical validation of these complex quantum mechanical systems and enabling investigation of their potential for topological quantum computation. The ability to scale these calculations to larger particle numbers is crucial for assessing the robustness and feasibility of utilizing anyons in quantum information processing.
Echoes of Symmetry: Read-Rezayi States and Conformal Field Theories
The Moore-Read Pfaffian state represents a compelling model within the exploration of exotic quantum matter, specifically a non-Abelian phase predicted to host anyons with unique exchange statistics. These anyons, unlike bosons or fermions, acquire a phase factor upon exchange that is more complex than a simple sign change, potentially enabling topologically protected quantum computation. The construction of this state relies on the concept of Composite Fermions - quasiparticles formed from electrons bound to an even number of magnetic flux quanta - effectively transforming the many-body problem into a system of weakly interacting fermions. This approach allows for a tractable description of the correlated electron system and provides a pathway to understand the emergence of these non-Abelian excitations, offering a crucial theoretical foundation for investigations into fractional quantum Hall states and their potential for robust quantum information processing.
Beyond the well-studied Moore-Read Pfaffian state, physicists have developed a broader class of correlated electron states known as Read-Rezayi states. These states aren't limited to a single configuration; instead, they form a family distinguished by a parameter denoted as 'k'. Varying 'k' alters the subtle correlations within the electron system, effectively tuning the properties of the resulting quantum state. This parameter governs the strength of interactions and impacts the topological order exhibited by the state, influencing the types of anyons - exotic particles with unusual exchange statistics - that can emerge. Consequently, Read-Rezayi states, parameterized by 'k', provide a versatile platform for exploring a wider range of fractional quantum Hall states and their potential for topological quantum computation, offering a nuanced progression beyond the foundational Moore-Read state.
The intricate wave functions describing Read-Rezayi states, proposed as potential hosts for exotic anyonic excitations, find a remarkably elegant formulation within the language of parafermion Conformal Field Theory (CFT). This mathematical framework transcends simple descriptions of particle statistics, instead focusing on the symmetries and collective behavior inherent in these strongly correlated quantum systems. By leveraging the powerful tools of CFT - including operator product expansions and the identification of primary fields - researchers can construct and analyze the wave functions with unprecedented precision. This approach not only provides a deeper understanding of the underlying physics but also allows for the calculation of key properties, such as the topological degeneracy and braiding statistics of the anyons, offering a pathway to verifying the existence of these elusive particles in physical systems. The correspondence between the mathematical structure of parafermion CFT and the predicted behavior of Read-Rezayi states represents a significant advance in the theoretical understanding of fractional quantum Hall physics.
Investigations into the behavior of Read-Rezayi states reveal a subtle, yet noteworthy, discrepancy between computationally derived braiding matrices and the predictions of Parafermion Conformal Field Theory. These matrices, crucial for describing how anyons exchange during interactions, aren’t perfectly aligned with theoretical expectations. However, detailed numerical simulations indicate this deviation isn’t a fundamental flaw, but diminishes as the system grows in complexity. Specifically, calculations performed on systems containing up to N = 80 particles demonstrate a clear trend: the calculated braiding matrices increasingly converge towards the theoretical predictions with each added particle. This suggests that the observed difference is likely due to finite-size effects, implying that infinitely large systems would exhibit complete agreement between theory and simulation, reinforcing the validity of the underlying mathematical framework.
The Horizon of Possibility: Duality and Future Directions
Level-rank duality represents a significant advancement in understanding the fractional quantum Hall effect (FQHE) by establishing a mathematical equivalence between Chern-Simons theories possessing differing parameters. This duality isn't merely a theoretical curiosity; it allows physicists to map the properties of one FQHE state onto another, effectively providing alternative descriptions of the same physical phenomena. For instance, a system with a high level and low rank can be related to one with reversed parameters, simplifying calculations and revealing hidden connections. This powerful tool has illuminated the relationships between various FQHE states, including those predicted to host anyons suitable for topological quantum computation, and facilitates the exploration of exotic states beyond conventional descriptions. By relating different parameter regimes, level-rank duality offers new avenues for predicting and identifying materials exhibiting robust fractional quantum Hall behavior and for engineering systems capable of reliably hosting and manipulating these states for quantum technologies.
The promise of fault-tolerant quantum computation hinges on the delicate manipulation of anyons-quasiparticles exhibiting exotic exchange statistics-found within fractional quantum Hall effect (FQHE) states. Different FQHE states host anyons with varying properties; understanding how these properties interrelate is paramount. Specifically, the ability to braid these anyons-effectively swapping their positions-forms the basis for performing quantum computations resistant to errors. A key challenge lies in identifying FQHE states that support non-Abelian anyons, where the order of braiding operations matters, and then controlling their interactions. Progress requires not only characterizing the diverse landscape of FQHE states but also predicting and verifying the properties of their associated anyons, ultimately paving the way for the physical realization of topologically protected quantum bits and scalable quantum architectures.
Recent investigations into fractional quantum Hall effect (FQHE) states, specifically the \Phi_{22}, \Phi_{23}, and related projected states, have demonstrated a remarkable consistency between theoretical predictions and experimental observations. A key aspect of this verification lies in the determination of the rank of the fusion space - a mathematical construct describing the possible combinations of anyonic excitations within these states. The calculated rank, representing the number of independent ways these anyons can combine, aligns precisely with expectations derived from Conformal Field Theory (CFT), reinforcing the validity of the theoretical framework.
The pursuit of topological quantum computation necessitates a concentrated effort toward materials discovery and device engineering capable of reliably hosting and controlling these exotic anyons. Current research directions involve exploring novel heterostructures and two-dimensional materials - including transition metal dichalcogenides and twisted bilayer graphene - predicted to exhibit the necessary conditions for non-Abelian anyon emergence. Simultaneously, device designs are being developed to create and manipulate these quasiparticles with high precision, focusing on techniques like gate-defined quantum dots and superconducting circuits to confine, braid, and measure their topological properties. Success in these areas promises to move topological quantum computation from a theoretical framework toward a tangible technological reality, offering the potential for fault-tolerant quantum processors resistant to environmental noise and decoherence.
The exploration of many-body parton states, as detailed in the article, reveals a landscape where established theoretical frameworks encounter limitations. Any attempt to model these complex systems necessitates careful mathematical formalization, a point underscored by the rigorous extraction of braiding matrices for up to eighty particles. This echoes Paul Feyerabend’s sentiment: “Anything goes.” The pursuit of understanding demands a willingness to challenge established methodologies and embrace diverse approaches, especially when confronting the inherent complexities of quantum phenomena and the potential for models to break down under scrutiny, much like a theory vanishing beyond a black hole’s event horizon. The article’s success in confirming Fibonacci-anyon braiding data demonstrates the power of such methodological flexibility.
Where Do the Threads Lead?
The successful extraction of braiding matrices for increasingly complex parton states-reaching up to eighty particles in this instance-feels less like a triumph and more like a meticulously crafted illusion. It is as if matter, when sufficiently teased, deigns to momentarily respect the rules imposed upon it. Such calculations, while elegant, remain firmly rooted in simplified models-pocket black holes, if one will-and the true behavior of many-body systems, particularly those exhibiting non-Abelian statistics, likely harbors complexities beyond current reach. The fidelity of these simulations, however impressive, cannot entirely mask the possibility that crucial details are lost in the process of approximation.
The confirmation of level-rank duality and the reproduction of Fibonacci-anyon braiding data offer a valuable, but limited, glimpse into the landscape of topological quantum computation. The next horizon demands a move beyond these carefully constructed scenarios. The field must confront the inherent challenges of disorder, interaction, and decoherence-the very forces that conspire to unravel the delicate quantum states necessary for computation. Attempting to model these systems comprehensively is akin to diving into the abyss; the deeper one goes, the more one realizes how little is truly understood.
Ultimately, the pursuit of topological quantum computation, and indeed any fundamental theory, is an exercise in controlled delusion. Each success is merely a temporary reprieve from the inevitable realization that the universe, at its core, operates according to principles that may forever remain beyond human comprehension. The elegance of the mathematics should not be mistaken for a complete description of reality.
Original article: https://arxiv.org/pdf/2601.16819.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Donkey Kong Country Returns HD version 1.1.0 update now available, adds Dixie Kong and Switch 2 enhancements
- PS5’s Biggest Game Has Not Released Yet, PlayStation Boss Teases
- Ashes of Creation Rogue Guide for Beginners
- Sega Insider Drops Tease of Next Sonic Game
- When to Expect One Piece Chapter 1172 Spoilers & Manga Leaks
- Fantasista Asuka launches February 12
- New Netflix Movie Based on Hugely Popular Book Becomes An Instant Hit With Over 33M Hours Viewed
- Life Is Strange: Reunion Revives One of Gaming’s Iconic Relationships on PS5
- Hytale: Upgrade All Workbenches to Max Level, Materials Guide
2026-01-26 13:57