Unzipping the Strong Force: Modeling String Breaking in QCD

Author: Denis Avetisyan

This review explores how effective string models and spatial Wilson loops can illuminate the complex process of string breaking – the fundamental mechanism behind quark confinement – within Quantum Chromodynamics.

String configurations in five dimensions reveal distinct behaviors dependent on connectivity, with a turning point coordinate <span class="katex-eq" data-katex-display="false">r_0</span> characterizing connected states and a light quark coordinate <span class="katex-eq" data-katex-display="false">r_{\bar{q}}</span> defining disconnected configurations at <span class="katex-eq" data-katex-display="false">y=0</span> and <span class="katex-eq" data-katex-display="false">y=Y</span>. — String configurations in five dimensions reveal distinct behaviors dependent on connectivity, with a turning point coordinate $r_0$ characterizing connected states and a light quark coordinate $r_{\bar{q}}$ defining disconnected configurations at $y=0$ and $y=Y$ .

An analysis of spatial string tension and its temperature dependence using AdS/CFT correspondence and pseudopotential models.

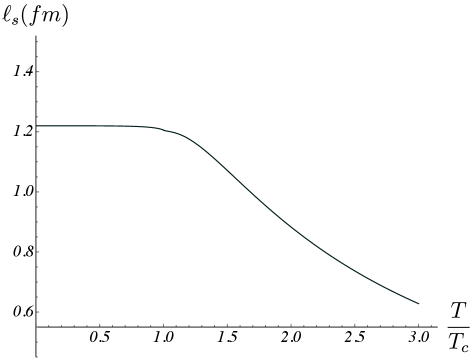
Understanding the dynamics of confinement in quantum chromodynamics (QCD) remains a central challenge, particularly regarding the transition from confining to deconfining phases. This is explored in ‘The spatial Wilson loops, string breaking, and AdS/QCD’, which investigates string breaking-a crucial mechanism for deconfinement-through the lens of spatial Wilson loops and the gauge/string duality. By analyzing the pseudopotential and introducing the concept of a spatial string breaking distance, the authors predict its temperature dependence within the $0-3T_c$ range for $SU(3)$ gauge theory. Can these findings, derived from an effective string model, provide further insights into the non-perturbative aspects of QCD and refine our understanding of the quark-gluon plasma?

Unveiling the Patterns of Confinement

Quantum Chromodynamics, the foundational theory of the strong force, elegantly describes interactions between quarks and gluons. However, the very nature of this force presents a significant computational challenge. Unlike electromagnetism, the strong force increases with distance, making traditional perturbative methods – those relying on approximations with small corrections – completely unreliable when attempting to model quark interactions. These methods, successful in other areas of physics, break down because the increasing force renders the necessary approximations invalid, leading to results that diverge and lack physical meaning. Consequently, physicists face a persistent struggle to accurately calculate the properties of hadrons – composite particles like protons and neutrons – directly from the principles of $QCD$ , necessitating the development of entirely new computational strategies.

The fundamental theory describing the strong force, Quantum Chromodynamics, runs into significant obstacles when applied to low-energy scenarios. Unlike electromagnetism, where interactions weaken with distance, the force between quarks increases as they are pulled apart. This counterintuitive behavior, known as confinement, renders standard perturbative methods – which rely on approximating interactions as small disturbances – completely ineffective. Attempting to calculate quark interactions at these energies results in diverging series, meaning the approximations become increasingly inaccurate the further they are pushed. Consequently, quarks are never observed in isolation; they are perpetually bound within composite particles called hadrons, such as protons and neutrons, due to this ever-strengthening force – a testament to the profound and complex nature of the strong interaction.

The very building blocks of matter familiar to us – protons and neutrons, collectively known as hadrons – owe their existence to a phenomenon deeply intertwined with quark confinement. Though described by Quantum Chromodynamics, the strong force binding quarks together doesn’t diminish with distance, leading to an inability to isolate individual quarks. This confinement isn’t merely a quirk of the force, but a fundamental aspect of hadron structure; it dictates that quarks are perpetually bound within these particles, shaping their mass, size, and interactions. Consequently, a thorough understanding of quark confinement is paramount to unraveling the internal architecture of all hadrons, and, by extension, a complete description of the visible matter in the universe. Without grasping why quarks remain confined, scientists are left with an incomplete picture of the forces governing the atomic nucleus and the stability of matter itself.

The limitations of conventional calculation methods in quantum chromodynamics (QCD) have spurred significant research into non-perturbative techniques. While traditional approaches excel when interactions are weak, they falter at the low energies where the strong force truly dominates, leading to the confinement of quarks within hadrons. Consequently, physicists are actively developing methods like lattice QCD, which discretizes spacetime to enable numerical solutions, and effective field theories, which simplify the complex interactions at low energies. These alternative strategies aim to bypass the difficulties inherent in perturbative calculations and provide a path toward a comprehensive understanding of hadron structure and the fundamental nature of the strong force, offering the potential to unlock the secrets hidden within the building blocks of matter.

A Holographic Mirror to the Strong Force

AdS/QCD is founded on the Gauge/String Duality, a conjecture stemming from string theory that posits an equivalence between quantum chromodynamics (QCD) and a theory of gravity in Anti-de Sitter (AdS) space. This duality proposes a mapping between strongly coupled gauge theories, like QCD which describes the strong nuclear force, and weakly coupled gravitational theories in the higher-dimensional AdS space. Specifically, the idea is that phenomena in the strong coupling regime of QCD – where traditional perturbative calculations fail – can be represented by classical, or weakly coupled, gravitational calculations within AdS space. This allows for the study of non-perturbative QCD phenomena, such as quark confinement and hadron masses, through gravitational principles. The AdS space itself is a maximally symmetric solution to Einstein’s equations with a negative cosmological constant, providing a specific geometric background for this duality.

The Gauge/String duality, central to AdS/QCD, facilitates the transformation of calculations involving strongly coupled quantum chromodynamics (QCD) into equivalent problems within classical gravity in Anti-de Sitter (AdS) space. This mapping is particularly advantageous because strong interaction problems in QCD are often analytically intractable due to the lack of a small coupling parameter; however, the dual gravitational problem in AdS space frequently allows for analytical or numerical solutions. Specifically, quantities like hadron masses, decay constants, and form factors, which are difficult to compute directly in QCD, can be determined by calculating corresponding geometric quantities – such as the mass of a black hole or the frequency of gravitational waves – within the AdS spacetime. This offers a non-perturbative computational pathway, circumventing the limitations of traditional perturbative QCD methods.

The five-dimensional framework of AdS/QCD constructs a gravitational dual to Quantum Chromodynamics (QCD) by representing the QCD vacuum as a five-dimensional spacetime with a specific metric. This metric incorporates a radial coordinate representing an energy scale, mapping the ultraviolet (UV) regime of QCD to the boundary of AdS space and the infrared (IR) regime to the AdS bulk. QCD degrees of freedom, such as quarks and gluons, are represented by string fluctuations propagating in this five-dimensional spacetime. The dynamics of these strings, governed by a string action, are then related to the interactions of hadrons in four-dimensional QCD. Specifically, the mass of a radially excited string mode corresponds to the mass of a hadron, enabling the calculation of hadron spectra and other observables from the five-dimensional gravitational solution.

The application of AdS/QCD as a holographic approach provides a means to investigate quark confinement and hadron properties without reliance on perturbative expansions. Traditional perturbative QCD methods become increasingly unreliable in the low-energy regime, where strong coupling effects dominate. AdS/QCD circumvents this limitation by reformulating strong interaction problems as calculations involving gravity in the AdS space, a weakly coupled regime allowing for analytical and numerical solutions. Specifically, the geometry of AdS space encodes the dynamics of the color force, enabling the study of confining potentials and the mass spectra of hadrons-such as mesons and baryons-through the analysis of gravitational fluctuations and string configurations within that space. This method allows for predictions regarding hadron properties that are otherwise inaccessible through conventional methods, and provides a framework for exploring the non-perturbative aspects of Quantum Chromodynamics.

The pseudopotential, exhibiting <span class="katex-eq" data-katex-display="false">V_{con}</span> and <span class="katex-eq" data-katex-display="false">V_{dis}</span> components, shifts with temperature, impacting the spatial string breaking distance which decreases as temperature increases from <span class="katex-eq" data-katex-display="false">T=0</span> to <span class="katex-eq" data-katex-display="false">T=1.5T_c</span> at <span class="katex-eq" data-katex-display="false">\Theta = 50\\,\\text{MeV}</span>. — The pseudopotential, exhibiting $V_{con}$ and $V_{dis}$ components, shifts with temperature, impacting the spatial string breaking distance which decreases as temperature increases from $T=0$ to $T=1.5T_c$ at $\Theta = 50\\,\\text{MeV}$ .

Unveiling the Confining Potential Through String Dynamics

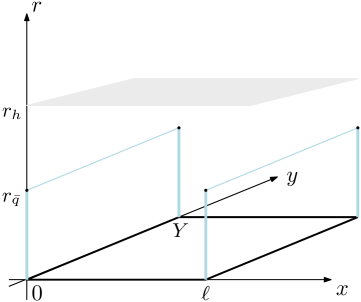
The potential energy experienced by quarks within strongly coupled gauge theories, such as Quantum Chromodynamics (QCD), is determined by the underlying geometry of a five-dimensional spacetime. Specifically, the “Soft Wall” model introduces a dynamically generated metric where the extra dimension’s scale factor varies, effectively creating a confining potential. This geometry leads to a potential that grows linearly with separation distance, a characteristic of confinement. The metric, described by $ds^2 = e^{2\phi(z)} (-dt^2 + dx^2 + dy^2 + dz^2)$ , where $\phi(z)$ is the warp factor dependent on the extra coordinate ‘z’, dictates the string embedding and consequently the potential seen by the quarks. A deeper value of ‘z’ corresponds to higher energy scales, and the exponential warp factor effectively screens the strong coupling at high energies while generating a linear confining potential at low energies.

The quark-antiquark potential is derived from calculations involving the area of string worldsheets, surfaces traced out by strings in spacetime. The Nambu-Goto action, expressed as $S = -T \in t d^2 \sigma \sqrt{det(h_{ab})}$ , where $T$ is the string tension and $h_{ab}$ is the induced worldsheet metric, is minimized to determine the classical string configuration. This minimization yields the potential energy, $V(r)$ , as a function of the separation distance, $r$ , between the quarks. The resulting potential exhibits a linear component at large distances, responsible for confinement, and a Coulombic component at short distances, describing the perturbative interaction. The string tension, $\sqrt{T}$ , directly corresponds to the slope of the linear potential and is a key parameter in understanding the strong force.

Spatial Wilson loops, calculated as the expectation value of a traced product of Polyakov loop operators in the spatial directions, provide a direct method for extracting the quark-antiquark potential. This potential, $V(R)$ , is fundamentally linked to the string tension, σ, through the relation $V(R) \approx \sigma R$ for large separations $R$ . Specifically, the string tension is determined by evaluating the slope of the potential obtained from the Wilson loop. The area of the Wilson loop, calculated via the Nambu-Goto action, is proportional to the potential energy, allowing for a precise determination of σ. This approach effectively maps the confining dynamics of Quantum Chromodynamics (QCD) to the geometry of the holographic dual space, allowing for quantitative comparisons with lattice QCD results.

The application of holographic principles to strong interaction physics provides a quantitative description of quark confinement. Specifically, calculations of the spatial string tension $\sigma_s$ derived from the holographic framework exhibit strong agreement with results obtained from lattice QCD simulations. This correspondence holds true across a temperature range up to approximately 2.5 to 3 times the critical temperature $T_c$ , beyond which the confining potential begins to deviate due to the phase transition to a quark-gluon plasma. This successful modeling of $\sigma_s$ validates the holographic approach as a viable tool for studying the non-perturbative regime of QCD and understanding the mechanisms responsible for hadronization.

String Fracture and the Birth of Hadrons

At sufficiently high energies, the strong force, typically confining quarks within hadrons, allows energetic strings to fracture. This process isn’t a literal breaking of a physical string, but rather a dynamic event where the energy concentrated within the color-flux tube – the string – becomes sufficient to create quark-antiquark pairs. These newly formed pairs then hadronize, combining to produce observable particles like mesons and baryons. Essentially, the energy of the string is converted into mass, manifesting as new hadrons. This phenomenon is crucial for understanding particle production in high-energy collisions, offering insights into the fundamental mechanisms governing the strong interaction and the transition from a deconfined quark-gluon plasma to the hadronic matter observed at lower energies.

The fragmentation of a high-energy string into observable hadrons isn’t a uniform process; it’s fundamentally shaped by the masses of the quarks involved. Lighter quarks, requiring less energy to create, facilitate string breaking at greater distances from the initial collision point, effectively increasing the probability of hadronization further away. Conversely, heavier quarks necessitate breaking closer to the source. This relationship dictates the distribution of created hadrons and impacts the overall characteristics of the resulting particle shower. Consequently, the mass of the quarks participating in the string fragmentation acts as a crucial parameter in modeling and understanding the transition from the initial energetic state to the observed multitude of hadrons, influencing both the types and spatial arrangement of the created particles.

The spatial string breaking distance, denoted as $ℓ_s$ , serves as a crucial parameter in characterizing hadronization – the process by which quarks and gluons coalesce into observable hadrons. This distance dictates where a color flux tube, or string, fractures to create new quark-antiquark pairs. Current models predict a remarkably stable behavior for $ℓ_s$ even across the phase transition between confined and deconfined states of matter. Specifically, the model anticipates that this breaking distance will remain finite – preventing unrealistic scenarios – and change smoothly as temperature and density fluctuate around the transition point. This predicted smoothness is significant, suggesting a gradual, rather than abrupt, shift in the mechanisms governing hadron formation, and offering a potential avenue for precisely mapping the quark-gluon plasma’s phase boundary.

Modeling the shift between confined and deconfined states of matter, such as the quark-gluon plasma, benefits from a dual analysis of string configurations – connected and disconnected. This approach examines how strings break and hadronize under varying temperatures and densities. Studies indicate that the off-diagonal element of the Hamiltonian, denoted as Θ, plays a crucial role in this transition, representing the interaction between different string configurations. Current estimations place Θ at approximately 50 MeV both at zero temperature ( $T=0$ ) and at 1.5 times the critical temperature ( $T=1.5T_c$ ), suggesting a relatively stable interaction strength across this phase transition and providing a valuable parameter for refining theoretical models of hadron formation.

Charting Future Directions Beyond the Horizon

The Anti-de Sitter/Quantum Chromodynamics (AdS/QCD) correspondence, a powerful tool for studying strong interactions, fundamentally depends on the assumed geometry of spacetime. This framework posits a connection between a gravitational theory in a higher-dimensional Anti-de Sitter space and a gauge theory, like QCD, in one fewer dimension; however, a critical component of this duality is the presence of a horizon within the AdS space. This horizon acts as a boundary, influencing how information is translated between the two theories and dictating the behavior of strongly coupled phenomena. The existence and properties of this horizon are not inherent features of QCD itself, but rather a mathematical construct within the AdS framework, meaning the model’s accuracy is intrinsically linked to the validity of this geometric assumption. Consequently, deviations from this idealized horizon structure, or the consideration of geometries lacking one entirely, could significantly alter the holographic description of QCD, highlighting both a limitation and an avenue for refinement within the model.

Current applications of the AdS/QCD correspondence often employ simplified, static spacetime geometries as a foundational approximation of quantum chromodynamics. However, to achieve a more precise and nuanced understanding of strong interaction physics, researchers are actively investigating the incorporation of more realistic geometrical configurations and dynamical effects. This includes exploring geometries that move beyond the strict AdS space, potentially incorporating features like finite temperature or time-dependent backgrounds. By allowing the holographic model to evolve and respond to changes in energy or external stimuli, scientists aim to capture the complex, non-equilibrium behavior observed in real-world strong interaction systems – such as those created in heavy-ion collisions or within neutron stars – and ultimately improve the predictive power of this intriguing theoretical framework.

The behavior of quark-gluon plasma-a state of matter existing at extremely high temperatures-and the associated phase transition from hadronic matter remain crucial areas of inquiry for the AdS/QCD framework. This approach offers a unique opportunity to study the temperature dependence of Quantum Chromodynamics (QCD) by relating strongly coupled gauge theories to weakly coupled gravitational systems. Current investigations explore how the geometry of the AdS space changes with temperature, effectively modeling the deconfinement transition and chiral symmetry breaking observed in experiments like those at the Relativistic Heavy Ion Collider and the Large Hadron Collider. Precise mapping of these transitions within the holographic framework requires a deeper understanding of finite temperature effects and the development of more sophisticated models capable of capturing the complex interplay between quarks and gluons at extreme energies; future work aims to refine these models to predict the precise conditions under which the quark-gluon plasma forms and its subsequent properties, including viscosity and energy density.

Ongoing investigations are dedicated to bolstering the precision of the holographic duality, a theoretical framework connecting gravity and quantum field theory, with the ultimate goal of extending its reach to a more comprehensive understanding of the strong interaction. This refinement involves tackling the inherent approximations within current models and developing techniques to address dynamical effects, such as those arising from quark-gluon plasma and the behavior of hadrons at extreme conditions. Researchers aim to move beyond idealized scenarios and incorporate complexities like finite temperature and baryon density, potentially unlocking insights into phenomena currently inaccessible through traditional perturbative methods. Ultimately, this expanded application of holographic duality promises to illuminate the intricate dynamics governing nuclear matter and the fundamental forces at play within the subatomic realm.

The exploration within this paper, detailing spatial Wilson loops and string breaking in QCD, resonates with a fundamental principle of discerning order within complexity. It is through meticulous analysis of these loops – and the deviations observed during string breaking – that a deeper understanding of confinement emerges. This process mirrors Nietzsche’s assertion: “There are no facts, only interpretations.” The study doesn’t merely observe string breaking; it interprets the patterns within the spatial string tension to extrapolate the temperature dependence of the breaking distance, effectively constructing a narrative from the observed phenomena. Every deviation from expected behavior, as highlighted in this work, is not an error but an opportunity to uncover hidden dependencies within the strong force.

Beyond the Horizon

The analysis of spatial Wilson loops, while offering a tractable approach to understanding string breaking, inevitably highlights the limitations inherent in effective models. The pseudopotential employed, successful as it is in capturing qualitative trends, remains fundamentally an approximation – a map, not the territory. Future investigations must rigorously address the sensitivity of predictions to the specific form of this potential, and crucially, explore alternative parameterizations derived directly from lattice QCD calculations. A true test lies not simply in matching the temperature dependence of the string breaking distance, but in predicting other observables sensitive to the underlying dynamics of confinement.

Furthermore, the inherent connection between spatial and temporal Wilson loops deserves deeper scrutiny. While this work focuses on the spatial case, a comprehensive understanding of string breaking requires a unified framework. Exploring the interplay between these two perspectives could reveal subtle, yet crucial, differences in the mechanisms governing confinement and deconfinement. Such an investigation may require going beyond the simplified string models, incorporating aspects of genuine non-perturbative dynamics.

Ultimately, the pursuit of understanding confinement – and therefore, the strong force – is a quest for identifying the emergent patterns within a complex system. This work offers a valuable piece of that puzzle, but it serves as a reminder that the most interesting questions often lie at the edges of our current understanding – beyond the horizon of established models, where new patterns may yet be revealed.

Original article: https://arxiv.org/pdf/2602.16657.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/