Warping Spacetime: A New Path to Lorentz-Violating Gravity

Author: Denis Avetisyan

Researchers have developed a novel technique to generate a family of spacetime solutions within bumblebee gravity, offering insights into how Lorentz symmetry might be broken.

For Kerr-(A)dS spacetime, the ranges of energy and rotation parameter define regions where the associated bumblebee field remains globally real or transitions to imaginary values, demarcated by critical curves and influenced by the cosmological constant <span class="katex-eq" data-katex-display="false">\lambda=\Lambda m^{2}</span>, with the dashed line indicating the threshold where the black hole becomes extremal. — For Kerr-(A)dS spacetime, the ranges of energy and rotation parameter define regions where the associated bumblebee field remains globally real or transitions to imaginary values, demarcated by critical curves and influenced by the cosmological constant $\lambda=\Lambda m^{2}$ , with the dashed line indicating the threshold where the black hole becomes extremal.

This work utilizes the Hamilton-Jacobi equation and a vector field to construct exact Kerr-Newman-(A)dS and other spacetimes, characterized by geodesic parameters, within the framework of bumblebee gravity’s Lorentz violation.

Lorentz invariance, a cornerstone of modern physics, faces increasing scrutiny from both theoretical and experimental fronts. This motivates explorations of effective field theories allowing for its violation, as addressed in ‘Exact Kerr-Newman-(A)dS and other spacetimes in bumblebee gravity: employing a novel generating technique’. Here, we present a novel technique for constructing exact solutions in bumblebee gravity-a theory featuring a dynamical Lorentz-violating vector field-by leveraging the Hamilton-Jacobi equation and associating the bumblebee field with geodesic curves in a background spacetime, yielding a class of solutions parameterized by these curves. Does this approach offer a systematic pathway to explore the broader landscape of Lorentz-violating gravitational solutions and their phenomenological implications?

Unveiling Asymmetries: The Quest for a More Complete Universe

Despite its century-long reign as the preeminent description of gravity, General Relativity exhibits limitations that suggest it may be an incomplete picture of the universe. While accurately predicting phenomena from planetary orbits to the bending of light, the theory breaks down at singularities – points of infinite density like those within black holes or at the very beginning of the universe – indicating a need for a more fundamental framework. This realization has spurred investigations into potential violations of Lorentz symmetry, a cornerstone of both relativity and quantum mechanics, which posits that the laws of physics are the same for all observers in uniform motion. The search for such violations isn’t about disproving relativity, but rather finding the more complete theory that encompasses it – a theory where Lorentz symmetry might emerge as an approximation valid only at low energies, much like Newtonian gravity approximates General Relativity in weaker gravitational fields. Consequently, physicists are developing increasingly sensitive experiments designed to detect minute deviations from Lorentz invariance, hoping to uncover clues about the true nature of gravity at the most fundamental level.

At the most fundamental scales of reality, established principles of symmetry, particularly Lorentz invariance-the idea that the laws of physics are the same for all observers in uniform motion-face challenges from cutting-edge theoretical frameworks. Both String Theory and Loop Quantum Gravity, independently developed attempts to reconcile gravity with quantum mechanics, suggest that Lorentz symmetry may not be absolute, but rather an approximation valid only at lower energies. These theories posit that the very fabric of spacetime might exhibit a granular or foamy structure at the Planck scale, introducing minute violations of Lorentz invariance. Such violations wouldn’t manifest as a complete breakdown of physics, but rather as subtle modifications to established physical laws, potentially altering the speed of light for different energies or introducing new, extremely weak interactions. Detecting these predicted deviations is a major focus of contemporary physics, requiring experiments capable of probing spacetime at unprecedented levels of precision and energy.

The pursuit of Lorentz symmetry violation demands a shift in gravitational modeling, compelling physicists to develop and investigate modified gravity theories. These frameworks intentionally deviate from the established tenets of General Relativity, incorporating terms that allow for subtle breaches of Lorentz invariance and, crucially, offer avenues for experimental detection. Rather than simply seeking to disprove existing models, this approach proactively designs theoretical landscapes where such violations would manifest as measurable effects – minute variations in the speed of light, anomalous particle interactions, or deviations from predicted gravitational forces. By deliberately introducing these possibilities into the theoretical structure, scientists can formulate precise predictions and design experiments sensitive enough to potentially reveal the universe’s hidden asymmetries, ultimately testing the very foundations of spacetime itself.

Bumblebee Gravity: A Vector Field Approach to Symmetry Breaking

Bumblebee gravity represents an extension of General Relativity achieved through the introduction of a vector field, termed the ‘bumblebee field’. Unlike General Relativity, which is predicated on Lorentz symmetry – the principle that the laws of physics are the same for all observers in uniform motion – bumblebee gravity intentionally incorporates mechanisms to break this symmetry. This is accomplished by assigning the bumblebee field a specific mathematical structure and dynamics, allowing it to interact with spacetime and potentially explain phenomena currently unaddressed by standard models. The bumblebee field is not simply an added component; its inclusion fundamentally alters the gravitational interaction, leading to modifications in predictions related to gravitational waves and the behavior of matter in strong gravitational fields.

The non-zero Vacuum Expectation Value (VEV) of the bumblebee field is a fundamental characteristic differentiating it from fields with zero VEV in standard models. This VEV represents the average value of the field in the vacuum state – the lowest energy state possible. A non-zero VEV indicates that the vacuum is not devoid of field activity, and crucially, it’s this constant, non-zero presence that spontaneously breaks Lorentz symmetry. Lorentz symmetry, a cornerstone of special relativity, posits the equivalence of all inertial frames; the bumblebee field’s VEV introduces a preferred direction in spacetime, violating this symmetry and leading to observable effects like birefringence and variations in the speed of light dependent on its polarization and propagation direction. The magnitude of the VEV directly influences the strength of these symmetry-breaking effects.

The trajectory of the bumblebee field, as described within the Bumblebee Gravity model, is fundamentally dictated by geodesic curves. These curves represent the shortest path between two points in a curved spacetime, meaning the field’s evolution isn’t arbitrary but intrinsically linked to the underlying geometry. Mathematically, the bumblebee field’s four-vector $B^\mu$ satisfies the geodesic equation: $\frac{d^2 B^\mu}{d\lambda^2} + \Gamma^\mu_{\alpha\beta} \frac{dB^\alpha}{d\lambda} \frac{dB^\beta}{d\lambda} = 0$ , where λ is an affine parameter and $\Gamma^\mu_{\alpha\beta}$ are the Christoffel symbols defining the spacetime’s connection. Consequently, any deviation of the bumblebee field from a straight line in flat spacetime is a direct manifestation of spacetime curvature and the field’s interaction with that curvature.

The ranges of energy and the Carter constant determine whether the bumblebee field is globally real (green) or imaginary (red), with the transition boundary marked by black curves, and a special case <span class="katex-eq" data-katex-display="false">C=4m^2</span> ensuring global reality even at zero energy for spacelike fields <span class="katex-eq" data-katex-display="false">\epsilon=+1</span> but not timelike fields <span class="katex-eq" data-katex-display="false">\epsilon=-1</span>. — The ranges of energy and the Carter constant determine whether the bumblebee field is globally real (green) or imaginary (red), with the transition boundary marked by black curves, and a special case $C=4m^2$ ensuring global reality even at zero energy for spacelike fields $\epsilon=+1$ but not timelike fields $\epsilon=-1$ .

Mapping Spacetime: The Hamilton-Jacobi Formalism in Action

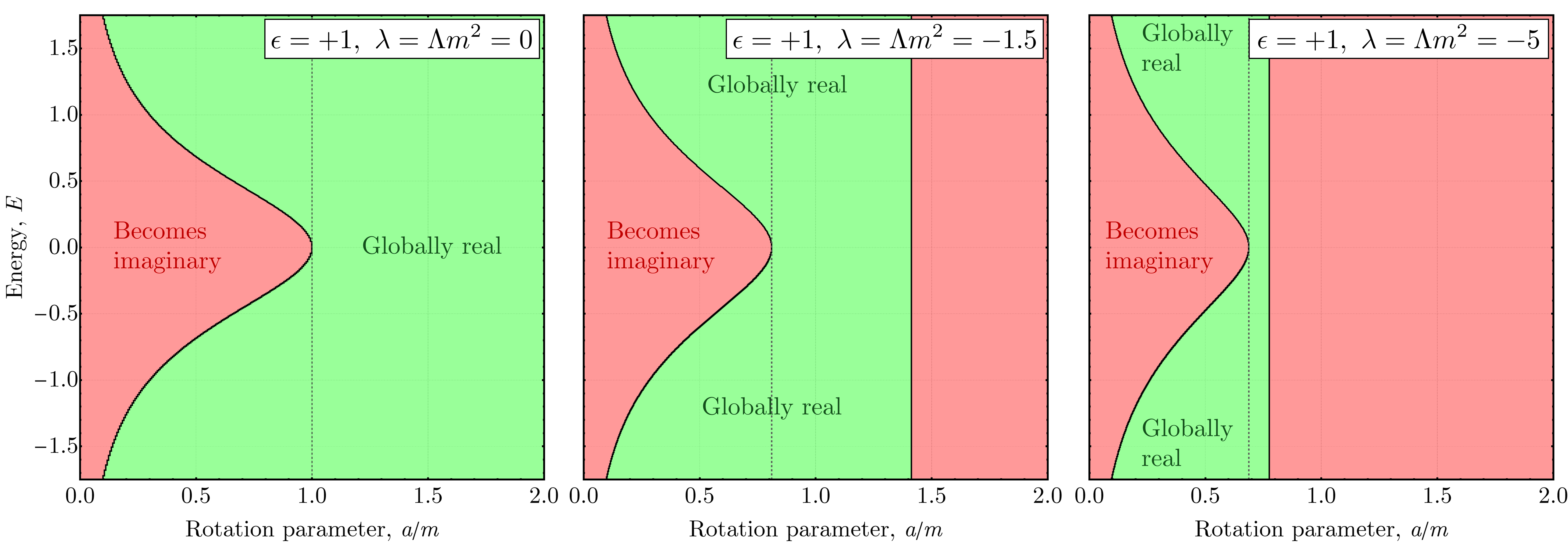
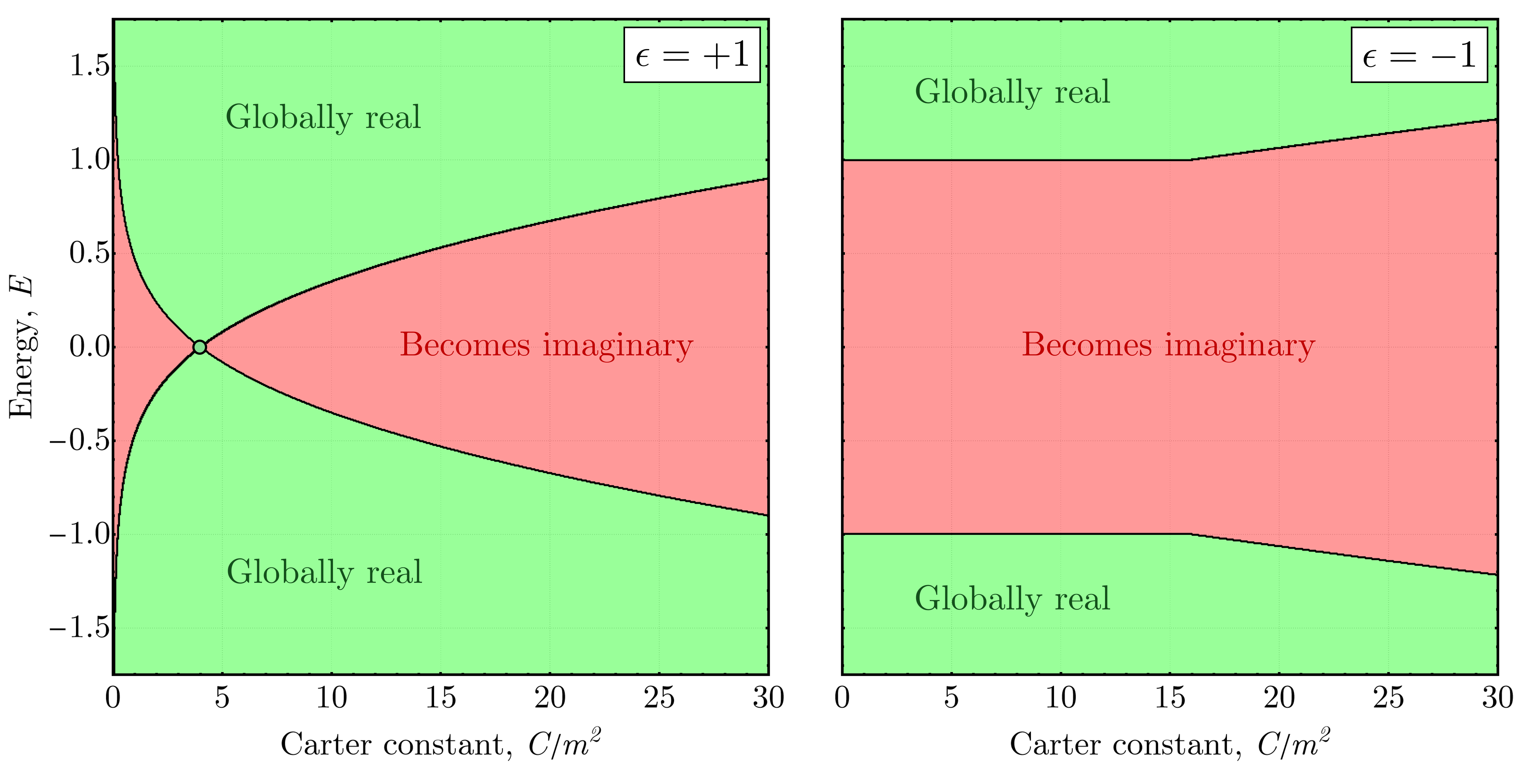
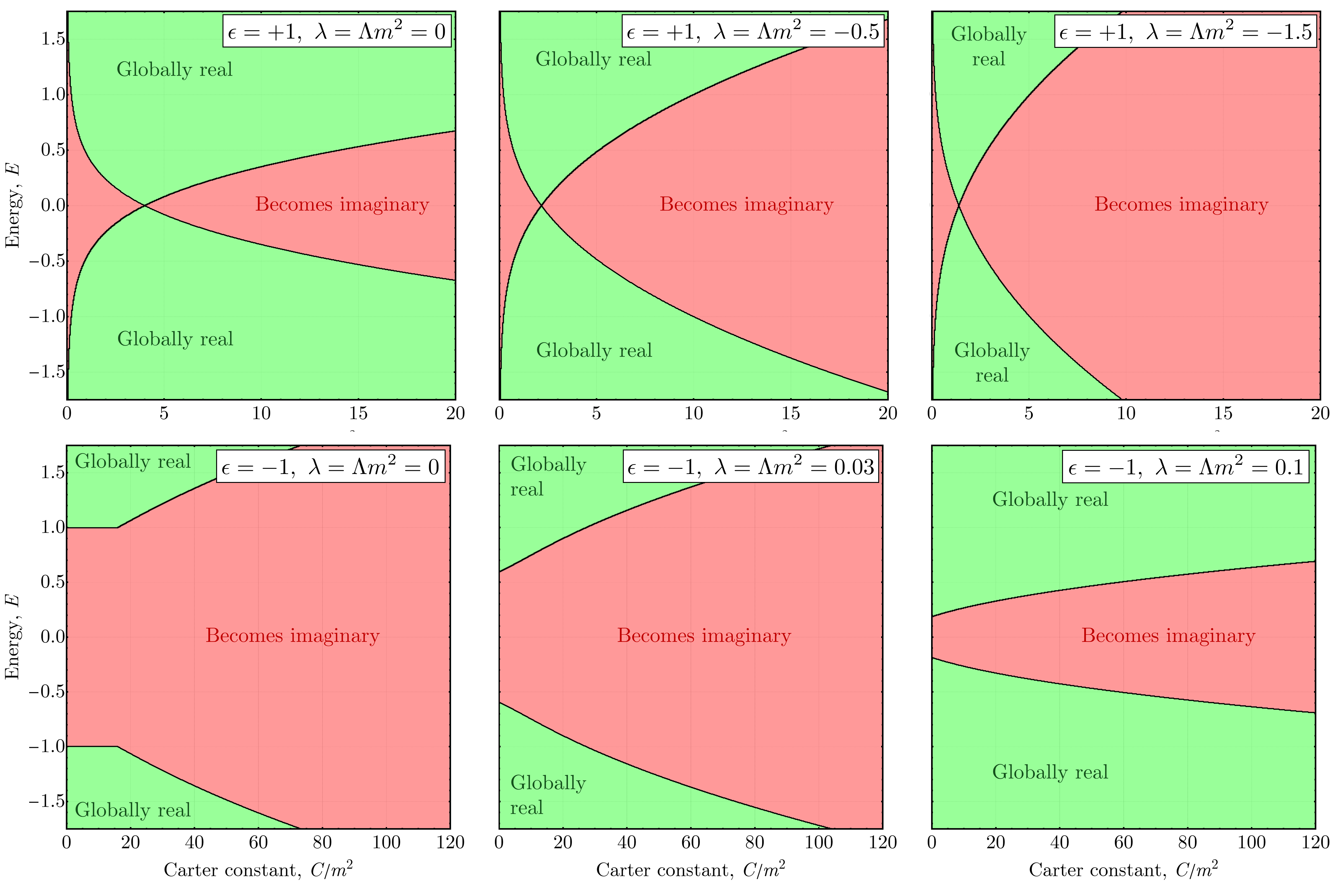
The Hamilton-Jacobi equation offers a systematic approach to obtaining solutions for bumblebee gravity by leveraging existing background metrics. This method is particularly effective because it allows for the direct derivation of solutions parameterized by conserved quantities – specifically, the Energy $E$ , Angular Momentum $L$ , and the Carter Constant $C$ . These constants represent integral motions within the spacetime and significantly simplify the solution process, effectively reducing the complexity of solving the geodesic equation and describing particle trajectories within the bumblebee gravity framework. The resulting solutions are expressed in terms of these separating constants, providing a complete description of the system’s dynamics.

The Separation of Variables technique is a standard approach to solving partial differential equations, including the Hamilton-Jacobi equation as applied to bumblebee gravity. This method involves expressing the solution as a product of functions, each dependent on a single independent variable. By transforming the original equation into a set of ordinary differential equations – one for each independent variable – the complexity is significantly reduced. Specifically, the Hamilton-Jacobi equation, which often involves multiple intertwined variables, is decomposed into a series of more manageable, uncoupled equations. Successful application of Separation of Variables relies on identifying a coordinate system appropriate to the symmetry of the problem, allowing for the independent variables to be clearly defined and the decomposition to proceed effectively, ultimately yielding solutions expressed as $\Psi(t,r,\theta,\phi) = R(r) \Theta(\theta) \Phi(\phi)$ .

The Kerr-Newman-Taub-NUT-AdS spacetime serves as a foundational metric for generating solutions within the Hamilton-Jacobi formalism due to its inherent complexity and the inclusion of multiple physically relevant parameters. This spacetime incorporates the effects of rotation (Kerr), electric charge (Newman), a cosmological constant leading to Anti-de Sitter space (AdS), and the Taub-NUT metric representing a non-multiply connected spacetime with a gravitational dipole moment. The metric’s complexity allows for the investigation of a wide range of gravitational phenomena and serves as a suitable background for deriving solutions characterized by conserved quantities like energy, angular momentum, and the Carter constant, essential for describing particle trajectories in the spacetime. Mathematically, it is described by a metric tensor $g_{\mu\nu}$ which accounts for these combined effects, making it a versatile starting point for solving the Hamilton-Jacobi equation and exploring bumblebee gravity solutions.

The stability of the bumblebee field in Reissner-Nordström-(A)dS spacetime depends on the energy <span class="katex-eq" data-katex-display="false">EE</span> and charge parameter <span class="katex-eq" data-katex-display="false">q/m</span>, with green regions indicating global reality and red regions indicating imaginary values, bounded by black curves and demarcated by the extremal black hole condition shown as a dashed line. — The stability of the bumblebee field in Reissner-Nordström-(A)dS spacetime depends on the energy $EE$ and charge parameter $q/m$ , with green regions indicating global reality and red regions indicating imaginary values, bounded by black curves and demarcated by the extremal black hole condition shown as a dashed line.

Implications for Spacetime and Beyond: Toward a More Complete Model

The Kerr-Newman-Taub-NUT-AdS spacetime represents a compelling solution in general relativity, distinguished by its inherent ability to model both cosmic expansion and electromagnetic phenomena within a single framework. This spacetime isn’t merely a mathematical construct; it naturally accommodates a cosmological constant, Λ, directly influencing the universe’s accelerating expansion, alongside an intrinsic electromagnetic field. Unlike simpler spacetimes requiring these elements to be artificially imposed, the Kerr-Newman-Taub-NUT-AdS solution integrates them as fundamental properties of the geometry itself. This arises from the spacetime’s complex topology-a blend of Kerr (rotating black hole), Newman (electric charge), Taub-NUT (magnetic monopole), and Anti-de Sitter (negative curvature) characteristics-creating a self-consistent model where gravity, rotation, charge, and cosmic expansion are interwoven aspects of a unified structure. Consequently, it offers a rich environment for investigating the interplay between these forces and exploring potential connections between black holes, cosmology, and electromagnetism.

To navigate the complexities of the bumblebee field’s interaction with spacetime, researchers utilize Effective Field Theory, a powerful tool in modern physics. This approach deliberately sidesteps a complete, fundamental description of the field’s origin, instead treating it as an external influence – a pre-existing condition impacting the surrounding gravitational environment. By focusing on the observable effects of this external influence, calculations become significantly more manageable without sacrificing crucial accuracy at lower energy levels. This simplification allows for a detailed investigation of how the bumblebee field modifies spacetime geometry and its potential implications for particle behavior, effectively isolating the field’s influence for focused analysis and paving the way for testable predictions.

The search for physics beyond the Standard Model gains a potential pathway through the Standard Model Extension (SME), which allows for the coupling of novel fields – such as the bumblebee field – to established particles. This framework doesn’t simply posit the existence of this field, but provides a mathematical structure for how it might interact with matter and energy. Crucially, the bumblebee field isn’t merely a theoretical construct; under specific conditions – notably when the angular momentum parameter $L=0$ , and within defined ranges of Energy $E$ and the Carter constant $C$ – the field demonstrates global reality. This means the field’s effects aren’t localized or transient, but represent a consistent, measurable influence on spacetime and potentially, on particle behavior, opening doors to experimental verification through precision measurements and searches for subtle violations of Lorentz invariance.

The stability of the Schwarzschild-(A)dS black hole’s bumblebee field, determined by its energy <span class="katex-eq" data-katex-display="false">EE</span> and Carter constant <span class="katex-eq" data-katex-display="false">CC</span>, transitions between globally real behavior (green) and instability (red) depending on the cosmological constant and whether the field is spacelike or timelike. — The stability of the Schwarzschild-(A)dS black hole’s bumblebee field, determined by its energy $EE$ and Carter constant $CC$ , transitions between globally real behavior (green) and instability (red) depending on the cosmological constant and whether the field is spacelike or timelike.

The presented research meticulously constructs solutions within bumblebee gravity, a framework intentionally designed to explore Lorentz violation. This endeavor echoes a fundamental philosophical concern: the implications of altering foundational principles. As Søren Kierkegaard observed, “Life can only be understood backwards; but it must be lived forwards.” Similarly, this work proceeds by building from established spacetime geometries-the ‘lived forward’ aspect-while simultaneously investigating the consequences of introducing a Lorentz-violating vector field, effectively a retrospective examination of altered foundations. The technique, rooted in the Hamilton-Jacobi equation, provides a systematic method to understand how deviations from established physics might manifest, demonstrating a responsibility to not only create functional models but also to consider their potential implications for our understanding of spacetime itself.

Beyond the Buzz: Charting a Course for Bumblebee Gravity

The construction of exact solutions in bumblebee gravity, while mathematically elegant, invites scrutiny beyond the immediate satisfaction of obtaining them. Someone will call it progress, and someone may stumble over the implicit assumptions baked into these geometries. The reliance on background spacetimes-Kerr-Newman, (A)dS-presupposes a pre-existing structure onto which Lorentz violation is grafted. The true test lies not in reproducing known results, but in predicting novel phenomena absent in standard general relativity, phenomena detectable and distinguishable from other proposed modifications to gravity.

The technique’s dependence on geodesic parameters, while facilitating solution generation, also highlights a limitation. It begs the question: are these solutions merely a convenient parametrization of existing spacetime, or do they genuinely represent new physical configurations? Further exploration must address the physical interpretation of these parameters and their connection to measurable quantities. Efficiency without morality is illusion; similarly, mathematical ingenuity without physical grounding is a beautiful, but ultimately sterile, exercise.

The immediate path forward necessitates moving beyond vacuum solutions. The inclusion of matter fields-particularly those with intrinsic spin-may reveal subtle couplings to the bumblebee vector, potentially leading to observable effects. More importantly, a rigorous investigation of the theory’s stability-both classical and quantum-is paramount. Without it, these solutions remain tantalizing possibilities, but not a robust foundation for a physical theory.

Original article: https://arxiv.org/pdf/2601.16037.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Unveiling Asymmetries: The Quest for a More Complete Universe

Bumblebee Gravity: A Vector Field Approach to Symmetry Breaking

Mapping Spacetime: The Hamilton-Jacobi Formalism in Action

Implications for Spacetime and Beyond: Toward a More Complete Model

Beyond the Buzz: Charting a Course for Bumblebee Gravity

See also: