When Fermi’s Golden Rule Loses Its Touch

by

Author: Denis Avetisyan

New research reveals that decoherence significantly alters the predictions of Fermi’s Golden Rule for modeling electron dynamics, challenging long-held assumptions in quantum mechanics.

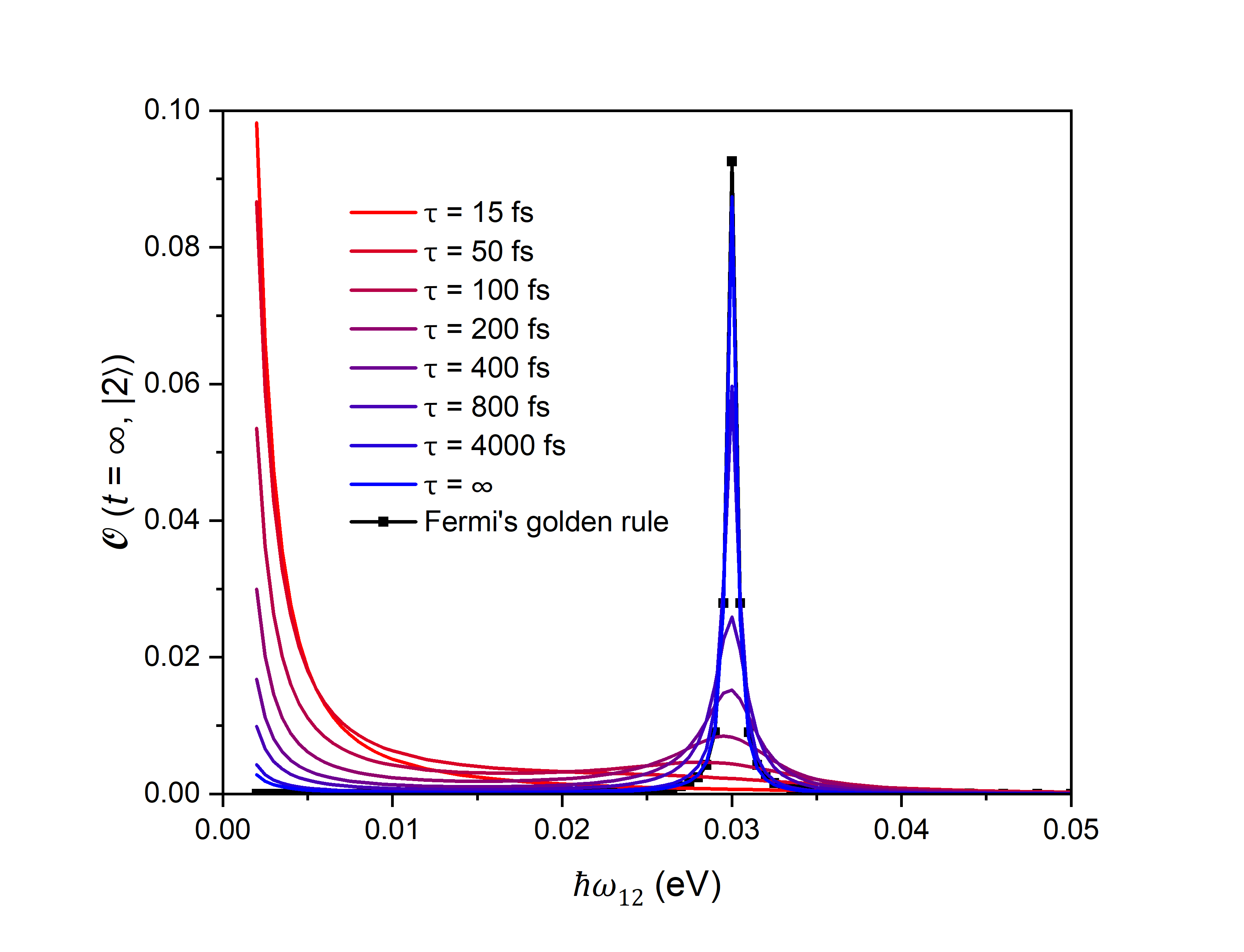
The system demonstrates that, at infinite time, the occupation of the $ \left|2\right\rangle$ state is determined by the energy gap - quantified as $ \left| \omega_{12} \right|$ - while maintaining a constant external perturbation frequency of 0.03 eV, starting from a fully occupied $ \left|1\right\rangle$ state.
The system demonstrates that, at infinite time, the occupation of the $ \left|2\right\rangle$ state is determined by the energy gap – quantified as $ \left| \omega_{12} \right|$ – while maintaining a constant external perturbation frequency of 0.03 eV, starting from a fully occupied $ \left|1\right\rangle$ state.

This review demonstrates deviations between Fermi’s Golden Rule and non-adiabatic molecular dynamics calculations when decoherence effects are prominent, emphasizing the need to account for decoherence in accurate modeling of carrier excitation and electron dynamics.

While Fermi’s Golden Rule provides a foundational framework for understanding transition rates in quantum systems, its original derivation neglects the increasingly important role of decoherence. This work, ‘The effects of decoherence on Fermi’s golden rule’, investigates how decoherence impacts the validity of this rule using non-adiabatic molecular dynamics calculations. We demonstrate significant deviations from Fermi’s Golden Rule when decoherence times are short, across both fixed and adiabatic bases, and illustrate this effect with first-principles calculations on monolayer $\mathrm{WS_2}$. As quantum technologies advance and ultrafast dynamics are explored, how can we refine theoretical models to accurately capture the influence of decoherence on carrier transitions and electron dynamics?

The Limits of Perturbation Theory: A System’s Response to Influence

The calculation of electronic transitions often begins with Fermi’s Golden Rule, a seemingly straightforward approach that, in practice, depends heavily on approximations. This rule essentially treats the interaction causing the transition as a small disturbance to the system, allowing physicists to calculate the probability of moving from one energy state to another. However, this relies on the principle of weak perturbation theory, demanding that the strength of this interaction be significantly smaller than the inherent energies within the system. While effective in many scenarios, this approximation introduces limitations; it assumes the system doesn’t dramatically change its behavior under external influence, and it often neglects the complex interplay with the surrounding environment. Consequently, the accuracy of predictions derived from Fermi’s Golden Rule diminishes when dealing with strong external fields or systems where these perturbative conditions aren’t met, highlighting the need for more sophisticated techniques to accurately model excited state dynamics.

The efficacy of established methods for describing quantum transitions diminishes considerably when systems are subjected to intense external fields or significant environmental interactions. Standard calculations, built on the assumption of minor disturbances to the system, begin to falter as these perturbations become comparable to or larger than the intrinsic energy scales of the quantum system. This is because the approximations used to simplify the calculations-treating the external influence or environmental coupling as a small correction-no longer hold true. Consequently, the resulting predictions regarding excited state lifetimes and transition probabilities can deviate substantially from experimental observations, demanding more sophisticated techniques capable of accurately accounting for these strong, non-negligible interactions and offering a more complete picture of the system’s dynamic behavior.

Predicting the behavior of excited electrons becomes markedly difficult when conventional computational techniques are applied to strong external stimuli or complex environments. These established methods, reliant on approximations, falter in ‘non-perturbative regimes’ where the usual simplifying assumptions break down, resulting in substantial inaccuracies. This limitation is particularly pronounced in materials possessing relatively small energy gaps – specifically those around 0.056 to 0.12 electron volts – where even modest external fields can induce significant deviations from predicted excited state dynamics. Consequently, understanding and accurately modeling phenomena like light absorption, energy transfer, and chemical reactivity in these systems requires moving beyond traditional approaches and embracing more sophisticated theoretical frameworks capable of capturing these complex interactions.

The occupation of the initial fully occupied state evolves differently under external perturbations at various frequencies, as demonstrated by comparisons between the Floquet-Gutzwiller-Recursion (FGR) method and numerical calculations using both fixed and adiabatic bases.
The occupation of the initial fully occupied state evolves differently under external perturbations at various frequencies, as demonstrated by comparisons between the Floquet-Gutzwiller-Recursion (FGR) method and numerical calculations using both fixed and adiabatic bases.

Decoherence: The Erosion of Quantum Coherence

Quantum decoherence represents the loss of quantum coherence, which is essential for phenomena like superposition and entanglement. This loss fundamentally alters the time evolution of electronic states by causing the off-diagonal elements of the system’s density matrix, which describe quantum coherence, to decay towards zero. Consequently, the system transitions from behaving as a purely quantum mechanical entity with predictable interference effects to exhibiting classical behavior characterized by probabilistic outcomes. The rate of this decay is determined by the strength of the coupling between the quantum system and its environment, effectively diminishing the system’s ability to maintain quantum information and impacting processes such as energy transfer and chemical reactions.

Decoherence arises from the unavoidable interaction of a quantum system with its surrounding environment. These environmental interactions, frequently manifested as phonons – quantized vibrational modes within a material – cause entanglement between the system and the environment. This entanglement effectively transfers quantum information from the system to the environment, leading to a loss of superposition and a reduction in the system’s ability to exhibit purely quantum behaviors. The rate of decoherence is directly proportional to the strength and density of these environmental interactions; stronger coupling and more numerous environmental degrees of freedom accelerate the process of transitioning from quantum to classical behavior. Consequently, maintaining coherence necessitates minimizing environmental interactions, often through isolation or operating at extremely low temperatures to reduce phonon populations.

Traditional perturbation theory, such as Fermi’s Golden Rule, assumes weak coupling between a quantum system and its environment and relies on approximations regarding short decoherence times. However, when decoherence times are not sufficiently short, these approximations break down, leading to inaccuracies in predicting system evolution. Accurate modeling of decoherence, therefore, necessitates a shift to methods that describe the complete quantum evolution of the system’s density matrix, $\rho$, governed by a master equation like the Lindblad equation or through direct propagation of the density matrix. These approaches account for the non-perturbative effects of environmental interactions and accurately capture the dynamics of coherence loss, even with finite decoherence times, providing a more realistic depiction of the system’s behavior.

Non-Adiabatic Molecular Dynamics: A First-Principles Approach to Dynamic Systems

Non-Adiabatic Molecular Dynamics (NAMD) is a simulation technique used to model the time-dependent behavior of quantum systems. Unlike traditional molecular dynamics which assumes a system remains on a single potential energy surface, NAMD explicitly accounts for transitions between multiple electronic states, crucial for simulating non-adiabatic processes like photoinduced reactions or charge transfer. The method propagates both the nuclear coordinates and the electronic wavefunction, allowing for the investigation of quantum effects such as tunneling and decoherence. Decoherence, the loss of quantum coherence due to interactions with the environment, is intrinsically included in NAMD via the propagation of the reduced density matrix, providing a realistic description of quantum dynamics in complex systems.

Non-Adiabatic Molecular Dynamics (NAMD) facilitates the simulation of real-time quantum dynamics by directly propagating the time-dependent Born-Oppenheimer molecular wavefunction. Unlike methods that rely on perturbative treatments of non-adiabatic couplings, NAMD solves the time-dependent Schrödinger equation without approximation, thereby avoiding limitations imposed by weak or strong coupling regimes. This is achieved by explicitly calculating the forces acting on the nuclei from the full electronic structure, typically using first-principles methods such as density functional theory or coupled cluster theory. Consequently, NAMD can accurately model a wider range of phenomena, including transitions between electronic states and non-radiative decay processes, without a priori assumptions about the coupling strength or the form of the potential energy surfaces.

The P-Matrix Method facilitates the computation of density matrix evolution within Non-Adiabatic Molecular Dynamics (NAMD) by directly propagating the density matrix in time, avoiding approximations inherent in wavefunction-based methods. This approach efficiently incorporates decoherence effects through a set of coupled differential equations governing the elements of the density matrix. Critically, the P-Matrix Method demonstrates consistency with Fermi’s Golden Rule – the established theory for transition rates – only in the limit of infinite decoherence time, where the system retains quantum coherence. As decoherence time decreases, deviations from Fermi’s Golden Rule emerge, highlighting the method’s ability to model non-perturbative decoherence phenomena and accurately capture the system’s dynamics when traditional perturbative approaches fail. The method’s efficiency stems from its ability to represent the density matrix in a reduced basis, scaling favorably with system size.

The occupation of the two-phonon TLS model, calculated numerically (black) and analytically (red, blue, gold, green) with specific phonon energies and electron-phonon coupling strengths, demonstrates strong agreement between methods.
The occupation of the two-phonon TLS model, calculated numerically (black) and analytically (red, blue, gold, green) with specific phonon energies and electron-phonon coupling strengths, demonstrates strong agreement between methods.

Simulating Dynamics in Monolayer WS2: A Validation Platform

Tungsten disulfide (WS2) reduced to a single atomic layer presents a uniquely suitable platform for assessing the accuracy of the Non-Adiabatic Molecular Dynamics (NAMD) method. This material exhibits a remarkably strong coupling between light and matter, meaning it readily absorbs and responds to electromagnetic radiation. Crucially, this interaction is accompanied by substantial decoherence effects – a loss of quantum coherence that quickly disrupts delicate quantum states. These characteristics create a demanding scenario for any simulation technique, as accurately modeling both the light-matter interaction and the resulting rapid decoherence is computationally challenging. The sensitivity of monolayer WS2 to these effects therefore allows for rigorous validation of NAMD’s ability to capture essential physical processes governing excited state dynamics in two-dimensional semiconductors and informs future studies of similar materials.

Numerical absorption modeling demonstrates that the NAMD approach effectively predicts excited state dynamics within monolayer WS2 by utilizing either a fixed or adiabatically evolving basis to represent the system. These simulations reveal a sensitivity to vibrational properties; variations in phonon energies – specifically 0.047 eV and 0.020 eV – and electron-phonon coupling (EPC) strengths of 0.00001 eV and 0.0001 eV significantly influence the material’s response to excitation. The accuracy of these predictions stems from the method’s ability to capture how these fundamental parameters modulate the excited state’s evolution, offering insights into the intricate interplay between electronic structure and lattice vibrations within this two-dimensional semiconductor.

Simulations demonstrate that decoherence – the loss of quantum information due to interactions with the environment – fundamentally alters how carriers become excited within monolayer WS2, with significant consequences for its optoelectronic behavior. The process isn’t a simple, instantaneous jump to a higher energy level, but rather a blurring of the excitation due to these interactions. This effect is particularly pronounced depending on the material’s band gap, which itself is sensitive to strain; systems experiencing tensile strain exhibit a smaller gap of approximately 0.056 eV, while compressive strain increases it to around 0.12 eV. Consequently, the rate of decoherence, and therefore the efficiency of carrier excitation, varies considerably with these energy gap differences, directly influencing the material’s ability to absorb light and generate electrical current.

NAMD simulations of excited carriers reveal that tensile strain decreases the energy gap to 0.056 eV, while compression increases it to 0.12 eV from a stress-free baseline of 0.067 eV, considering phonon energies of 0.046 and 0.020 eV with respective electron-phonon coupling strengths of 0.007 and 0.016 eV from an initial fully occupied state on VBM-2.
NAMD simulations of excited carriers reveal that tensile strain decreases the energy gap to 0.056 eV, while compression increases it to 0.12 eV from a stress-free baseline of 0.067 eV, considering phonon energies of 0.046 and 0.020 eV with respective electron-phonon coupling strengths of 0.007 and 0.016 eV from an initial fully occupied state on VBM-2.

The study’s findings regarding the deviation of Fermi’s Golden Rule from Non-adiabatic Molecular Dynamics calculations when decoherence is prominent underscores a critical principle: systems are interconnected, and altering one component necessitates understanding the whole. This resonates with the observation that infrastructure should evolve without rebuilding the entire block. As Richard Feynman once stated, “The difficulty lies not in the new ideas, but in escaping from the old ones.” The research challenges the conventional application of Fermi’s Golden Rule, demanding a shift in perspective to incorporate decoherence effects for accurate modeling of electron dynamics. Ignoring these systemic influences, as the study demonstrates, leads to inaccurate predictions and a failure to grasp the complete behavior of the system.

Where Do We Go From Here?

The divergence between Fermi’s Golden Rule and non-adiabatic molecular dynamics, as demonstrated in this work, isn’t a failure of either method, but a symptom of simplifying assumptions. The standard formulation of Fermi’s Golden Rule implicitly assumes a well-defined, separable bath – a convenient fiction. Real systems, of course, do not neatly partition into system and environment. Decoherence, the gradual erosion of quantum coherence, represents the system’s relentless negotiation with its surroundings, and ignoring it introduces error that scales with complexity. The pursuit of ever-more-accurate calculations cannot proceed by merely increasing computational power; it demands a more nuanced understanding of these environmental interactions.

Future work must focus on systematically incorporating decoherence into tractable, scalable models. The challenge lies not in calculating decoherence – that is, in principle, straightforward – but in representing its effects without introducing intractable computational overhead. A fruitful avenue may involve exploring coarse-grained descriptions of the environment, focusing on the essential modes that drive decoherence, rather than attempting a full, atomistic treatment. The goal isn’t to eliminate approximations, but to make them conscious approximations, fully aware of their limitations and trade-offs.

Ultimately, the true cost of freedom – the freedom to treat subsystems in isolation – is the accurate modeling of their dependencies. This work serves as a reminder that elegance in theoretical models isn’t about minimizing complexity, but about understanding the fundamental constraints that shape behavior. A seemingly simple system can reveal layers of complexity when viewed through the lens of its environment, and good architecture, like a well-designed organism, will be invisible until it breaks.

Original article: https://arxiv.org/pdf/2511.21238.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-11-28 20:52