Author: Denis Avetisyan
New research reveals how relativistic effects alter the fundamental limits on how quickly quantum states can change, impacting the precision of phase measurements.
This work derives first-order relativistic corrections to the quantum speed limit for Gaussian states and proposes experimental verification using balanced homodyne detection and pilot-aided phase tracking.
Fundamental limits on the rate of quantum evolution, encapsulated by the quantum speed limit, typically neglect relativistic effects despite their relevance to precision technologies. This is addressed in ‘Relativistic Quantum-Speed Limit for Gaussian Systems and Prospective Experimental Verification’, which derives first-order relativistic corrections to these limits for Gaussian states, revealing a dependence on both amplitude and squeezing. These corrections manifest as an increased lower bound on evolution time and a measurable phase drift, potentially detectable within minutes using current balanced homodyne detection techniques. Could these findings unlock new sensitivities in quantum technologies operating in high-velocity or strong-field regimes, and further refine our understanding of the interplay between relativity and quantum mechanics?
The Quantum Speed Limit: Beyond Classical Intuition
The rate at which a quantum system changes its state – its dynamics – underpins a vast and growing range of technologies. Precise control over these dynamics is paramount in quantum computation, where the speed of gate operations directly impacts processing power. Similarly, in quantum metrology – the science of ultra-precise measurements – faster state evolution enables higher resolution and sensitivity. Beyond these fields, understanding temporal dynamics is also critical for designing efficient quantum sensors, developing new materials with tailored properties, and probing fundamental aspects of quantum mechanics itself. Consequently, a thorough investigation into the limits and capabilities of quantum state evolution is not merely a theoretical exercise, but a crucial step toward realizing the full potential of quantum technologies and expanding the frontiers of scientific knowledge. The ability to manipulate and measure these changes with increasing speed and accuracy is therefore central to ongoing research and innovation.
The realm of quantum mechanics operates under principles fundamentally different from those governing everyday experience. Classical physics, built on predictable trajectories and definite properties, breaks down when applied to particles existing as probabilities and superpositions. Consequently, simply applying classical notions of speed or time to quantum evolution proves inadequate; a rigorous mathematical framework is essential. This isn’t merely a matter of refinement, but a necessary shift in perspective, as quantities once considered absolute become inherently uncertain, linked by relations like the Heisenberg uncertainty principle. Establishing precise limits on how quickly a quantum state can change demands abandoning intuitive assumptions and embracing the probabilistic nature of quantum reality, which necessitates a completely new set of tools and definitions to accurately describe and predict quantum dynamics.
The conventional understanding of quantum speed limits relies heavily on the Time-Energy Uncertainty Relation, which dictates a fundamental trade-off between the precision with which energy and time can be known. However, for the increasingly sophisticated demands of quantum technologies, this relation proves insufficient; achieving truly optimized control requires refinements that account for relativistic effects. Specifically, calculations demonstrate that the limits on how quickly a quantum state can evolve are impacted by corrections proportional to $ϵ^2t^2$, where $ϵ$ represents the relative velocity and $t$ is time. These relativistic corrections, though often negligible at lower energies, become critically important when dealing with fast-evolving quantum systems, such as those envisioned for advanced quantum computation and high-precision sensing, necessitating a more nuanced approach to defining and achieving optimal quantum control.
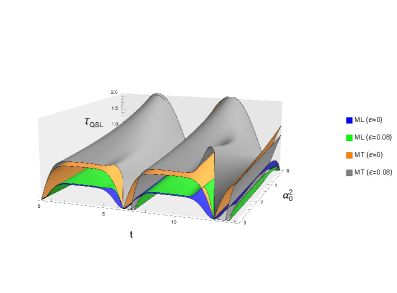
State Dependence: The Quantum Speed Limit Isn’t Universal
The established concept of a Quantum Speed Limit (QSL) does not represent a universal, fixed rate for quantum evolution. Instead, the QSL is state-dependent; the maximum speed at which a quantum system can evolve is intrinsically linked to the properties of its initial state. For example, a system initialized in a $Coherent State$ will exhibit a different QSL compared to one prepared in a $Squeezed State$. Coherent states, possessing a minimum uncertainty product, typically result in a more conservative speed limit. Conversely, squeezed states, characterized by reduced uncertainty in one observable at the expense of increased uncertainty in its conjugate variable, can, in principle, allow for faster evolution under specific conditions, though still constrained by the fundamental principles of quantum mechanics.
Squeezed states, generated through the application of a $Squeeze Operator$ to a vacuum or coherent state, exhibit reduced uncertainty in one quadrature of the electromagnetic field at the expense of increased uncertainty in the other. This manipulation of uncertainty allows for faster evolution of the quantum state in certain processes, as the time required for a given change is inversely related to the uncertainty in the relevant quadrature. While coherent states minimize uncertainty equally across both quadratures, squeezed states concentrate uncertainty, effectively lowering the minimum uncertainty in the quadrature governing the evolution and thus, theoretically enabling faster transitions than achievable with solely coherent states. The degree of speedup is dependent on the magnitude of the squeezing applied and the specific quantum process under consideration.
The $Mandelstam-Tamm$ and $Margolus-Levitin$ bounds represent state-dependent limits on the rate of quantum evolution, offering more precise constraints than a universal speed limit. The $Mandelstam-Tamm$ bound stipulates that the average frequency of change for a quantum state is limited by the uncertainty in energy divided by Planck’s constant, while the $Margolus-Levitin$ bound relates the maximum evolution speed to the square root of the energy dispersion divided by Planck’s constant. Importantly, these bounds are subject to first-order relativistic corrections; as velocities approach the speed of light, these corrections become significant and impact the variance of squeezed states. Specifically, relativistic effects alter the energy-time uncertainty relation, thus modifying the limits imposed by both bounds and influencing the achievable speed of evolution for systems initialized in squeezed states.
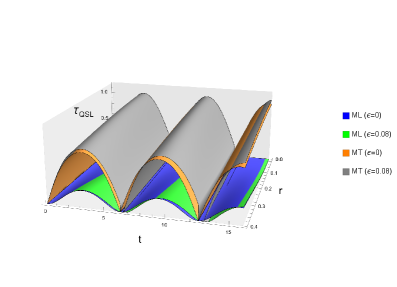
Precision and Limits: Measuring the Quantum Dance
Determining the rate of quantum evolution necessitates the accurate characterization of changes in a quantum state. A common experimental technique employed for this purpose is Balanced Homodyne Detection. This method involves interfering the signal mode with a strong coherent state, known as the local oscillator, and measuring the quadrature amplitude difference. The resulting photocurrent is proportional to the change in the signal state’s quadrature amplitude, allowing for reconstruction of the state’s time evolution. The sensitivity of this measurement is crucial, as even small deviations from the actual evolution can introduce errors in determining the speed of the quantum process. Careful calibration and noise reduction are essential components of utilizing Balanced Homodyne Detection for precise timing of quantum phenomena, particularly when investigating dynamics approaching the quantum speed limit.
The Cramer-Rao Bound establishes a lower limit on the variance of any unbiased estimator used to determine an unknown parameter within a quantum state. Specifically, the bound states that the variance of an estimator for a parameter $\theta$ cannot be less than $1/I_Q(\theta)$, where $I_Q(\theta)$ represents the Quantum Fisher Information. The Quantum Fisher Information, calculated as the minimum over all possible measurements, quantifies the amount of information a quantum state carries about the parameter being estimated; higher values of $I_Q(\theta)$ indicate greater sensitivity and thus a tighter lower bound on achievable precision. Consequently, maximizing the Quantum Fisher Information through optimized measurement strategies is crucial for approaching the limits of quantum metrology and achieving the highest possible precision in parameter estimation.
Optimizing quantum measurement strategies is crucial for approaching both the theoretical quantum speed limit and the precision bounds imposed by the Cramer-Rao bound. This optimization involves minimizing measurement-induced disturbance while maximizing information gain about the evolving quantum state. A key consideration in high-precision measurements, particularly those over extended durations, is accounting for deterministic phase drift resulting from relativistic effects. This drift is quantifiable as $γt^2$, where γ represents the relativistic parameter and t is the measurement time. Effective strategies must therefore not only minimize standard quantum limits but also compensate for, or accurately model, this deterministic phase accumulation to maintain precision and accurately determine the rate of quantum evolution.
Relativity’s Shadow: Phase Sensitivity and the Quantum Realm
For quantum systems demanding extreme precision – such as atomic clocks or certain interferometry experiments – relativistic corrections are no longer negligible refinements but fundamental components of accurate modeling. These corrections arise from Einstein’s theory of special relativity and manifest as subtle shifts in energy levels and, consequently, in the phase of a quantum state. As precision increases, the sensitivity of the system to these relativistic effects grows proportionally; even seemingly small relativistic contributions can introduce measurable phase drift. This phase sensitivity is particularly pronounced when dealing with high-energy particles or in strong electromagnetic fields, where relativistic effects become more substantial and directly influence the quantum dynamics. Ignoring these corrections would introduce systematic errors, limiting the achievable precision and potentially obscuring the true quantum behavior of the system.
The intricacies of quantum dynamics at relativistic speeds necessitate a robust theoretical framework, and the Foldy-Wouthuysen expansion provides just that – a systematic approach to incorporate special relativity into quantum mechanical calculations. This technique essentially decouples particle and antiparticle components of a wave function, allowing physicists to isolate and address relativistic corrections that would otherwise be obscured. By iteratively applying transformations, the expansion generates an effective Hamiltonian that accurately describes the system’s evolution, even when particles approach the speed of light. The resulting corrections aren’t merely perturbative add-ons; they fundamentally alter the energy levels and transition probabilities, becoming crucial for understanding phenomena in high-energy physics, quantum field theory, and even precision spectroscopy where subtle relativistic effects can significantly impact observable results. Through this method, complex relativistic quantum dynamics become amenable to calculation, enabling predictions and interpretations of experiments probing the boundaries of quantum and relativistic regimes.
Relativistic corrections fundamentally reshape the boundaries of quantum speed limits, becoming especially pronounced when dealing with high-energy particles or those subjected to intense electromagnetic fields. Traditional understandings of quantum evolution assume a constant speed, but relativistic effects introduce a time-dependent shift in the phase of a quantum state. This manifests as a measurable phase drift that doesn’t increase linearly with time, but rather scales quadratically – proportional to $γt^2$, where γ represents the Lorentz factor, and $ϵ^2t^2$ encapsulates the strength of the relativistic perturbation. Consequently, the effective speed at which quantum information can propagate is altered, demanding precise consideration of these corrections in high-precision experiments and advanced quantum technologies. The quadratic dependence on time provides a unique signature, allowing researchers to not only detect but also characterize the influence of relativistic phenomena on quantum dynamics.
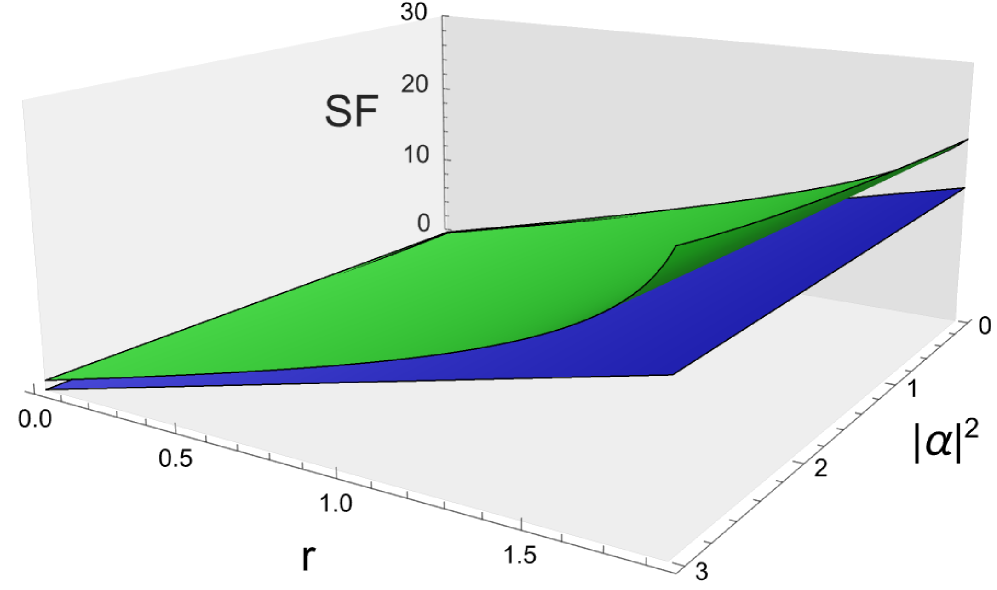
Quantum Communication: A Future Defined by Precision
The foundation of secure communication protocols, such as Gaussian-modulated coherent state Quantum Key Distribution (GMCS CV-QKD), rests on the ability to meticulously prepare and maintain quantum states, alongside an exceptionally accurate determination of the signal’s phase. These systems encode information onto properties of light, demanding precise control over parameters like amplitude and polarization to ensure secure key generation. Phase estimation is particularly crucial; even slight inaccuracies introduce errors that compromise security and reduce the rate at which a secret key can be established. Consequently, advanced techniques are continuously developed to minimize phase drift and enhance the fidelity of transmitted quantum states, pushing the limits of what’s achievable in quantum information transmission and bolstering the practical viability of unconditionally secure communication networks.
Quantum communication systems, particularly those employing protocols like GMCS CV-QKD, are acutely vulnerable to phase errors introduced by imperfections in the communication channel. These errors degrade the fidelity of quantum states, directly impacting the security and efficiency of key exchange. Pilot-aided phase tracking techniques address this challenge by intentionally embedding known “pilot” signals alongside the quantum information. By carefully analyzing these pilots, the system can estimate and compensate for the accumulated phase drift, effectively stabilizing the quantum link. This precise phase estimation is not merely a technical correction; it directly translates to a maximization of the key rate – the speed at which secure keys can be generated. Without such tracking, the achievable communication distance and security levels would be drastically limited, hindering the practical deployment of quantum communication networks.
Realizing the transformative potential of quantum communication hinges on exceeding established quantum speed limits and achieving unprecedented measurement precision. Current protocols, while theoretically secure, are susceptible to phase errors that degrade performance; therefore, advancements in minimizing these errors are paramount. Recent theoretical work suggests that, with optimized measurement strategies and averaging techniques, the subtle effects of relativistic phase drift – a consequence of special relativity impacting quantum signals over distance – could become detectable within approximately 15 minutes. This level of sensitivity represents a significant leap forward, promising not only enhanced security for quantum key distribution but also the possibility of utilizing these systems to probe fundamental aspects of spacetime and test the limits of quantum mechanics itself. Further refinement of these techniques is expected to unlock even greater key rates and extend the reach of secure quantum communication networks.
The pursuit of precision, as demonstrated in this exploration of relativistic corrections to the quantum speed limit, highlights a fundamental aspect of human endeavor. Even with increasingly sophisticated models-here, examining coherent and squeezed states-the underlying mechanisms remain tethered to inherent limitations. As Albert Einstein observed, “The important thing is not to stop questioning.” This research, detailing how relativistic effects influence phase sensitivity and offering pathways for experimental verification via balanced homodyne detection, exemplifies this relentless questioning. The study implicitly acknowledges that even with perfect information, individuals – and by extension, the scientists constructing these models – often prioritize refining existing frameworks rather than embracing entirely novel ones, a predictable flaw in the algorithm of discovery.
The Horizon of Speed
The refinement of the quantum speed limit, even with first-order relativistic corrections, doesn’t truly address the question of why systems evolve as they do, merely how quickly. It’s a comforting exercise, quantifying the inevitable, but it presupposes an inherent drive towards change, a sort of quantum restlessness. The framework presented here, focused on coherent and squeezed states, neatly sidesteps the messiness of truly complex systems – those where entanglement isn’t a pristine laboratory effect, but a pervasive, noisy reality. Future work will inevitably push towards those boundaries, attempting to model decoherence not as a limitation, but as an integral part of the speed limit itself.
The proposed experimental verification, reliant on balanced homodyne detection and pilot-aided phase tracking, feels less like a triumph of engineering and more like a sophisticated attempt to observe a boundary that, fundamentally, resists direct observation. Every measurement introduces a story, a narrative of certainty imposed upon an uncertain state. The precision gained will undoubtedly be impressive, but it will always be a precision about a story, not a direct apprehension of reality.
One suspects the real challenge isn’t pushing the limits of measurement, but accepting their inherent limitations. The speed at which a quantum system evolves is ultimately less interesting than the reasons why it chose that particular path. People don’t make decisions; they tell themselves stories about decisions, and quantum systems are no different. The next frontier lies not in faster observation, but in better storytelling.
Original article: https://arxiv.org/pdf/2511.20707.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Hazbin Hotel season 3 release date speculation and latest news
- 10 Chilling British Horror Miniseries on Streaming That Will Keep You Up All Night
- Where Winds Meet: How To Defeat Shadow Puppeteer (Boss Guide)
- Dolly Parton Addresses Missing Hall of Fame Event Amid Health Concerns
- 🤑 Crypto Chaos: UK & US Tango While Memes Mine Gold! 🕺💸
- Jelly Roll’s Wife Bunnie Xo Addresses His Affair Confession
- The Mound: Omen of Cthulhu is a 4-Player Co-Op Survival Horror Game Inspired by Lovecraft’s Works
- 5 Perfect Movie Scenes That You Didn’t Realize Had No Music (& Were Better For It)
- World of Warcraft leads talk to us: Player Housing, Horde vs. Alliance, future classes and specs, player identity, the elusive ‘Xbox version,’ and more
- You Won’t Believe What Happens to MYX Finance’s Price – Shocking Insights! 😲
2025-11-27 13:03