Spinning Black Holes: How Magnetic Fields Supercharge Particle Acceleration

Author: Denis Avetisyan

---

New research reveals a surprising relationship between magnetic field strength and energy extraction around rotating black holes, potentially explaining the origin of high-energy particles in extreme astrophysical environments.

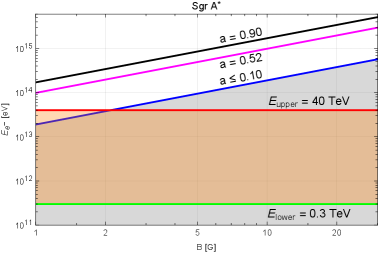
This study details a non-monotonic enhancement of the Magnetic Penrose Process in Kerr-Bertotti-Robinson spacetime and its implications for electron acceleration around astrophysical black holes.

Conventional models of energy extraction from rotating black holes typically predict monotonic enhancements with increasing magnetic field strength, yet observations suggest more complex behavior. This work, ‘Non-Monotonic Enhancement of the Magnetic Penrose Process in Kerr-Bertotti-Robinson Spacetime and its Implication for Electron Acceleration’, investigates the Magnetic Penrose Process within the Kerr-Bertotti-Robinson spacetime-a rotating black hole embedded in a uniform electromagnetic field-revealing a surprising non-monotonic relationship between field strength and energy extraction efficiency. We demonstrate that the event horizon and static limit surface exhibit an initial expansion followed by contraction with increasing magnetic field, potentially enabling electron acceleration to ultra-high energies near supermassive black holes. Could this non-monotonic behavior resolve discrepancies between theoretical predictions and observed high-energy astrophysical phenomena?

---

The Spacetime Echo: Foundations of a Rotating Abyss

Rotating black holes represent far more than simple gravitational traps; they are profoundly dynamic distortions of spacetime itself, playing a critical role in powering some of the universe’s most energetic phenomena. Unlike their non-rotating counterparts, these astrophysical objects possess a ‘spin’ that drags spacetime around with them, creating a region known as the ergosphere where nothing can remain stationary. This twisting of spacetime isn’t merely a theoretical curiosity; it provides a mechanism for extracting energy from the black hole, potentially fueling powerful jets of particles observed in active galactic nuclei and quasars. The complex interplay between gravity, rotation, and spacetime geometry in these systems dictates how matter accretes, how energy is released, and ultimately, how galaxies evolve – making the study of rotating black holes fundamental to understanding high-energy astrophysics and the universe at large.

While the Schwarzschild metric provided a foundational understanding of non-rotating black holes, accurately depicting the spacetime around rotating black holes necessitates the significantly more complex Kerr metric. This solution, derived directly from Einstein’s field equations, accounts for the black hole’s angular momentum, a crucial factor in astrophysical scenarios. Unlike its simpler predecessor, the Kerr metric describes a spacetime that is ‘dragged’ into rotation by the black hole itself, a phenomenon known as frame-dragging. This introduces an ergosphere, a region outside the event horizon where spacetime is twisted and objects are forced to co-rotate with the black hole. The mathematical intricacies of the Kerr metric, involving ellipsoidal rather than spherical symmetry, allow for a far more realistic representation of the spacetime distortions surrounding these rapidly spinning cosmic objects, and serve as a cornerstone for modeling phenomena like accretion disks and relativistic jets emanating from the vicinity of rotating black holes.

The universe isn’t neatly divided into gravity-only scenarios; strong electromagnetic fields frequently coexist with massive, rotating objects. Consequently, the Kerr-Bertotti-Robinson spacetime emerges as a refinement of the standard Kerr metric, incorporating a uniform electromagnetic field to model black holes in more realistic astrophysical conditions. This combined spacetime isn’t merely a mathematical exercise; it significantly alters the black hole’s surrounding geometry, influencing the shape and size of crucial features like the event horizon and the static limit surface. Researchers utilize this model to investigate how external magnetic fields affect the black hole’s properties, revealing that the event horizon radius, initially expanding with field strength as described by rh(B) = rh(0) + B²αh + O(B⁴), may exhibit contraction at sufficiently high magnetic field intensities. This nuanced interplay between gravity and electromagnetism offers insights into phenomena like jet formation and energy extraction from rotating black holes.

The spacetime surrounding a rotating black hole, as described by the Kerr-Bertotti-Robinson metric, is dramatically reshaped, most notably through the creation of the event horizon and the static limit surface – boundaries defining the black hole’s region of influence. The event horizon, beyond which nothing can escape, isn’t a fixed entity; its radius responds to external electromagnetic fields. Studies reveal that an increasing magnetic field initially expands the event horizon, a relationship mathematically expressed as rh(B) = rh(0) + B²αh + O(B⁴), where rh(B) is the horizon radius with field strength B, rh(0) is the radius without a field, and αh represents a constant related to the black hole’s properties. However, this expansion isn’t limitless; at sufficiently high field strengths, the event horizon radius is predicted to contract, suggesting a complex interplay between gravity and electromagnetism in these extreme environments and offering a potential mechanism for altering a black hole’s observable characteristics.

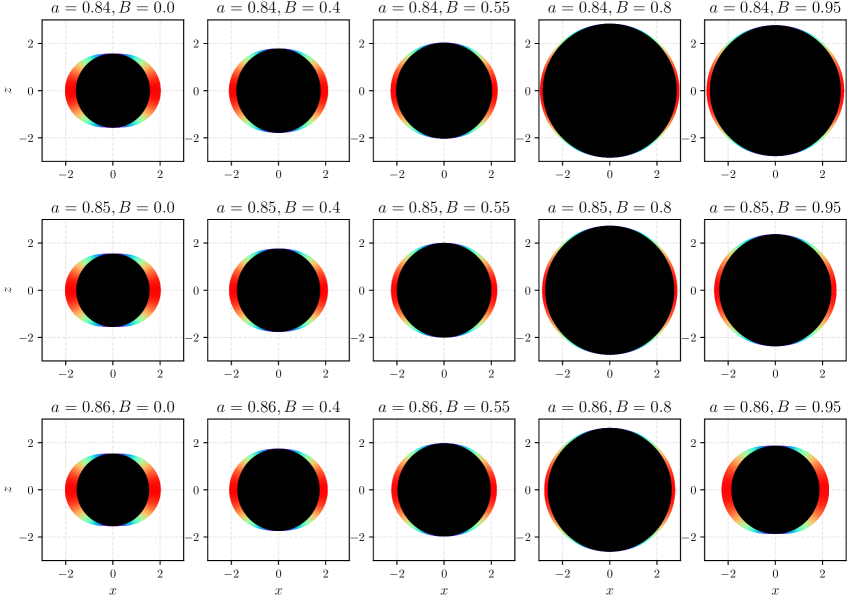
The Ergospheric Dance: Frame-Dragging and the Limits of Stationarity

The ergosphere is a uniquely relativistic region exterior to a rotating black hole’s event horizon. It is defined by the surface where the spacetime itself is dragged around the black hole at the same rotational velocity as the black hole’s surface. This effect, known as frame-dragging, isn’t a material entrainment but rather a consequence of the black hole’s mass-energy distorting the geometry of spacetime according to the principles of General Relativity. While outside the event horizon, it is impossible to remain stationary with respect to an observer at infinity within the ergosphere; all objects and particles are forced to co-rotate to some degree with the central mass. The shape and size of the ergosphere are determined by the black hole’s angular momentum and mass, being oblate due to the rotational forces.

The ergosphere’s spacetime distortion fundamentally alters particle behavior, compelling particles within it to co-rotate with the black hole. This isn’t a passive effect; the forced co-rotation results in an increase in the particle’s angular velocity relative to an observer at infinity. Consequently, a particle can, in principle, exit the ergosphere with more energy than it possessed upon entry, effectively extracting rotational energy from the black hole. This energy gain is achievable because the spacetime itself is doing work on the particle, increasing its energy through the forced co-rotation, and establishing a pathway for potential energy extraction processes.

The Innermost Stable Circular Orbit (ISCO) represents the minimum radius at which a test particle can maintain a stable orbit around a massive object, such as a black hole. Inside this radius, particles will inevitably spiral into the central mass. The location of the ISCO is directly dependent on the object’s spin; a rotating black hole possesses an ISCO that is closer to the event horizon than a non-rotating black hole. This difference is crucial for energy extraction because the closer the ISCO, the greater the potential energy available from particles orbiting at that radius. Consequently, the ISCO effectively sets an upper limit on the efficiency of energy extraction processes; any attempt to extract energy from particles closer than the ISCO would result in their immediate accretion, preventing useful energy recovery. The radius of the ISCO is a key parameter in modeling the efficiency of processes like the Penrose process and is calculated differently for charged and uncharged particles.

The spacetime geometry of the ergosphere enables theoretical energy extraction mechanisms, such as the Magnetic Penrose Process, due to the forced co-rotation of particles. Critically, the thickness of the ergoregion is not constant but is modulated by the presence of a magnetic field. This relationship is quantified by the equation r_{sl}(B, θ) = r_{sl}(0, θ) + B²r₂(θ) + O(B⁴), where r_{sl} represents the radius of the innermost stable circular orbit, B is the magnetic field strength, θ is the latitudinal angle, and r₂(θ) is an angularly dependent coefficient. The equation demonstrates that increasing magnetic field strength B leads to a contraction of the ergoregion, particularly pronounced at the equator, thereby influencing the efficiency and feasibility of energy extraction processes dependent on ergoregion geometry.

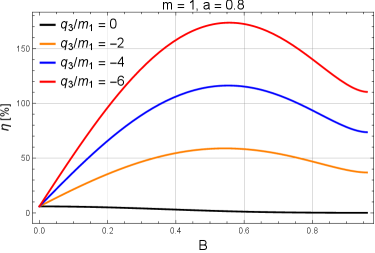
Harnessing the Abyss: The Magnetic Penrose Process and Energy Yield

The Magnetic Penrose Process (MPP) enables energy extraction from a rotating black hole by exploiting the Ergosphere, a region where spacetime is dragged along with the black hole’s rotation. Within the Ergosphere, particles can possess negative energy as observed at infinity. The MPP involves a particle with positive energy entering the Ergosphere, splitting into two particles – one with negative energy that falls into the black hole, and another with amplified energy that escapes to infinity. This process effectively reduces the black hole’s rotational energy, converting it into usable energy carried by the escaping particle. The efficiency of this energy transfer is dependent on the specific trajectories and energies of the interacting particles within the distorted spacetime of the Ergosphere.

The Magnetic Penrose Process (MPP) enhances energy extraction from rotating black holes by leveraging electromagnetic interactions. While the standard Penrose process relies solely on spacetime geometry to accelerate particles, the MPP introduces magnetic fields that provide an additional force on charged particles within the ergosphere. This electromagnetic force increases the particle’s energy gain during extraction, resulting in a higher efficiency compared to purely gravitational methods. Specifically, charged particles experience a Lorentz force \mathbf{F} = q(\mathbf{E} + \mathbf{v} \times \mathbf{B}) due to the combined electric and magnetic fields, boosting their final energy and increasing the overall energy extraction rate from the black hole’s rotational energy.

The energy extraction efficiency of the Magnetic Penrose Process (MPP) is directly proportional to the magnetic field strength surrounding the rotating black hole, but this relationship is not linear. While increasing magnetic field strength initially enhances energy yield by influencing particle trajectories within the ergosphere, the efficiency plateaus and ultimately decreases beyond an optimal field strength. This non-monotonic behavior contrasts with energy extraction processes in Kerr spacetime, which typically exhibit monotonic increases with field strength. Research indicates that exceeding this optimal magnetic field strength introduces factors that diminish the effectiveness of particle acceleration and energy transfer, limiting the maximum achievable electron energy to approximately 5.11 \times 10^{15} \text{ eV}.

Energy maximization via the Magnetic Penrose Process is predicated on the complex interplay of spacetime distortion within the ergosphere, particle interactions, and the strength of the surrounding magnetic field. Recent research indicates that energy extraction efficiency does not increase linearly with magnetic field strength, as observed in Kerr geometry; instead, efficiency exhibits a non-monotonic relationship, peaking at an optimal field strength before declining with further increases. Calculations based on this process estimate the maximum energy achievable by an electron to be approximately 5.11 \times 10^{15} eV, demonstrating the potential for substantial energy yields under optimized conditions.

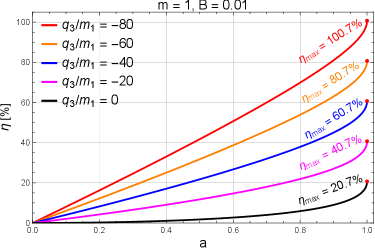
The pursuit of maximizing energy extraction from rotating black holes, as detailed within this study of the Magnetic Penrose Process, reveals a curious truth: optimization is often illusory. Attempts to achieve peak efficiency invariably encounter diminishing returns, a non-monotonic relationship dictated by the very forces one seeks to harness. This echoes a sentiment expressed by Søren Kierkegaard: “Life can only be understood backwards; but it must be lived forwards.” The study of KBR spacetime demonstrates a similar paradox – understanding the process requires retrospective analysis, yet the universe unfolds regardless of our comprehension, often defying simple, linear optimization. The architecture isn’t structure – it’s a compromise frozen in time, and so too is any attempt to perfectly control the chaotic dance around a black hole.

What Lies Beyond?

The exploration of energy extraction from rotating black holes, as demonstrated through the Magnetic Penrose Process in Kerr-Bertotti-Robinson spacetime, does not reveal a path to mastery, but rather a deepening awareness of inherent limits. The observed non-monotonic relationship between magnetic field strength and extraction efficiency is not an anomaly to be corrected, but a symptom of the system’s complexity-a reminder that architecture is how one postpones chaos. Attempts to optimize this process, to ‘tune’ the cosmos, will inevitably encounter unforeseen bifurcations, new instabilities masked by the initial conditions. There are no best practices-only survivors.

Future investigations will not likely yield a singular, scalable solution for harnessing energy from these extreme environments. Instead, focus should shift toward understanding the emergent properties arising from the interplay of gravitational and electromagnetic fields. The study of particle dynamics within these spacetimes is not merely about predicting trajectories, but about mapping the boundaries of predictability itself.

Ultimately, the true value of this work lies not in its potential for engineering, but in its contribution to a more nuanced understanding of the universe’s fundamental constraints. Order is just cache between two outages. The black hole does not offer energy; it offers a mirror-reflecting the limits of control and the inevitability of entropy.

---

Original article: https://arxiv.org/pdf/2601.09919.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

• Darkwood Trunk Location in Hytale

• Best Controller Settings for ARC Raiders

• Hytale: Upgrade All Workbenches to Max Level, Materials Guide

• Ashes of Creation Rogue Guide for Beginners

• Daredevil Is Entering a New Era With a Chilling New Villain (And We Have A First Look) (Exclusive)

• RHOBH’s Jennifer Tilly Reacts to Sutton Stracke “Snapping” at Her

• So Long, Anthem: EA’s Biggest Flop Says Goodbye

• 7 Announcements We’re Dying to See at Dragon Ball’s Genki Dama Festival This Month

• The Rip Ending Explained: Who’s The Traitor (And What Those Tattoos Are About) In Ben Affleck And Matt Damon Thriller

• Golden Globes 2026: Gracie Abrams And Paul Mescal Have Rare Date Night

2026-01-18 12:13